加权最小二乘估计与线性无偏最小方差估计的比较

孙晓杰

(四川大学数学学院,四川成都 610064)

加权最小二乘估计与线性无偏最小方差估计的比较

孙晓杰

(四川大学数学学院,四川成都 610064)

在已知的线性模型中,考虑加权最小二乘估计与线性无偏最小方差估计的结果的差异。发现在两种条件下,加权最小二乘估计与线性无偏最小方差估计的结果趋于一致。

加权最小二乘估计 线性无偏最小方差估计

1 引言

加权最小二乘估计与线性无偏最小方差估计是线性模型估计中最常使用的方法。本文主要讨论这两种方法在估计中结果有什么不同。

2 问题描述

Z=Xβ+ε(其中X 是m×n矩阵(已知)，β是1×n的列向量(要估计的未知参数)，ε为残差项，Z为观察值)。考虑用加权最小二乘估计和无偏线性最小方差两种方法对β进行估计，考虑这两种估计所得结果是否相等。

3 两种方法的比较

线性无偏最小方差估计：

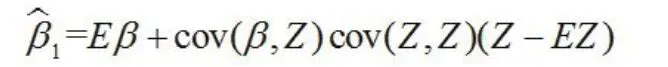
该估计的误差方差：

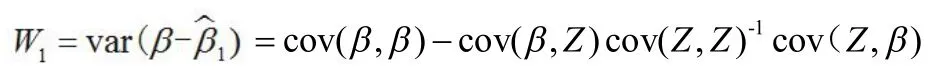
加权最小二乘估计：

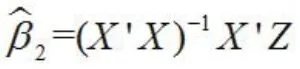
该估计的误差方差：

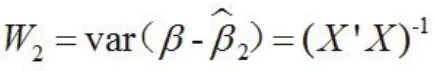
3.1 对W1进行变形

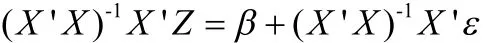
所以

将上面的式子(1)--(4)带入则

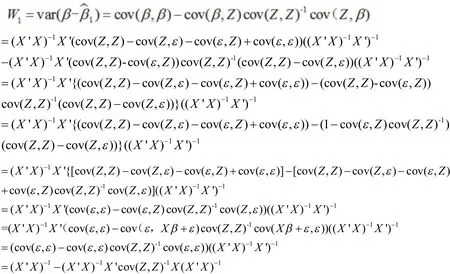
3.2 求差值

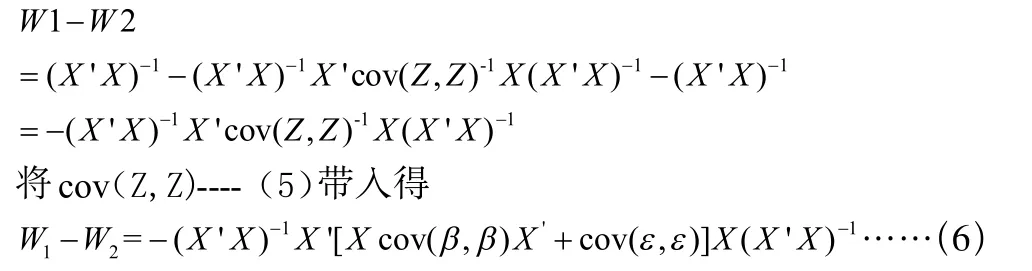
3.3 进一步考虑(6)式子,在两种可能情况下趋于0

[1]孙荣恒.应用数理统计(第3版) [M].科学出版社,2014年1月1日.

[2]Jun Shao.Mathematical statistics：exercises and solutions[M].世界图书出版公司.2010.

[3]Huart. David.Mathématiques et statistique[M].武汉大学出版社,2010.

[4]Hogg. Robert V.Introduction to mathematical statistics[M].Higher Education Press.2004.

[5]刘谢进,朱允民.最优加权最小二乘估计与线性无偏 最小方差估计性能比较[J].四川大学学报(自然科学版),2001年10月第38卷第5期.