对(1± 1)n 两种系数展开式上线性区域的解析初步——基于quot;牛顿三角形quot;性质的研究与探讨㈠

王以将 刘忠 王红霞

(1.江苏省阜宁县羊寨镇农业经济服务中心,江苏盐城 224415;2.桂林理工大学,广西桂林 541006)

对(1± 1)n两种系数展开式上线性区域的解析初步
——基于quot;牛顿三角形quot;性质的研究与探讨㈠

王以将1刘忠2王红霞2

(1.江苏省阜宁县羊寨镇农业经济服务中心,江苏盐城 224415;2.桂林理工大学,广西桂林 541006)

“杨辉-牛顿三角形”已经将二项系数的展开式表示为数图化的图形形式,然发现其延展出的可糅合性、命名性、滑动性、连贯性、线性区域这五种特性,可使牛顿三角形内任意两点间,都可建立起连贯性的关系式;将 (1± 1)n两形式的系数展开式及其示图,糅合成一个新的三角形“△”后,仍清晰反映两形式系数的不同角度与方向上的点、行、列之间的线性连贯关系,可发现更多性质,新产生性质公式275个。

性质(含公式) 应用公式 线性关系区域 不同角度与方向

二项式系数的展开已经组成“杨辉-牛顿三角形”,在此基础上,我们依据 (a+ b )n与 (a-b )n形式或合略称 (1± 1)n两形式所组成的三角形的可揉合性,结合成一个新的三角形“△”后,其各自部分仍保持原有的性质不变．通过数图化的图形形式,发现其延展出的可揉合性、命名性、滑动性、连贯性、线性区域这五种特性,其中最重要两点命名性、连贯性,可使牛顿三角形内任意两点都可建立起连贯的线性关系式．且由一点起经与有关行或列上的移动性连续运算是本文的主要方法与特点,可省却大量繁重的归纳演绎推导；故新三角形“△”,仍清晰反映不同角度与方向上的点、行、列之间的线性连贯关系,新产生性质公式275个。

1 新三角形“△”具有的五种特性

牛顿三角形对于 (1+ 1)n形式系数展开式采用了数字表示法,据此也可将 (1- 1)n形式三角形表示出来．并根据 (1± 1)n两形式三角形的五种特性所构成不同角度与方向上的线性区域及线性连贯关系。以示图形式作一简要描述,见图1-1。

(1)可揉合性。新三角形“△”,仍可以保持它们各自原有的一些性质定理的存在,同时以行n’为界线行置于 (1- 1)n的可视起始处,自然分为上、下各自部分,在阅读上仍较方便．

图1-1

(2)可命名性。除了行的概念外,图中有列的概念,即对每一斜向的列可进行命名．而斜列的表示法,如图:由上右至下左方向排列的分别称第1、2、3、…左斜列,用符号“1/”、“2/”、“3 /”、……表示；由上左至下右方向排列的分别称第1、2、3、…右斜列,用符号“1”、“2”、“3”、……表示。例某一点或(-),可表示在第n行上,同时在第“(m+1)/”上,也在第“(n-m+1)”上．从图形上反映标示位置,左斜列在图形右侧,右斜列在图形左侧。

(3)可滑动性。以界线行n’为滑动线,作上、下、左、右滑动,都可反映两形式的上、下各自部分的正、负符号的随机变化。如实现在计算机应用领域能自动控制滑动则更好。当处于 (1+ 1)n形式时,每项(点)前符号都属于正号；处于 (1- 1)n形式时,每上标为零与偶数位项时属于正号,每上标为奇数位项时属于负号。

(4)可连贯性。新三角形“△”内部,任一最小的倒等边三角形“ ▽”的三个相邻项(点)之间都存在6个互逆的关系式,由此外延,对应于某一原项(点)P0[称Cmn或(±)]的其它项(点)Pr,都存在对应于原点 P0的线性连贯关系式,且通过示图及移动运算式可得到推导[将“△”左或右外的项(点)的值为0时,在图形中用空项“□”符号表示其位置]。

(5)线性区域。若干对应于某一项(点)P0的其它项(点)Pr,都存在对应于原点P0的角度问题,可用公式0．5H)]来表达[I、H分别表示横、纵向上的移动运算步(项)数]。但公式使用起来多数情况下其角度难以确切表示．但某些角度仍可确切掌握清晰,例每相隔30度的0°、30°、60°、90°、120°、150°、180°、210° 、240°、270°、300°、330°这12个方向的对应角度项(点)。

根据科学出版社出版的,由胡国定等编写的《简明数学词典》2000年11月第1版第9章“组合数学-图论”中第495页的两处介绍组合数性质与组合恒等式[及同包含龙门书局出版社2002年1月第1版源流等编写的《发散课堂大思维》·高二代数(下)·试验本第158页],目前排列数、组合(数)恒等式有9个]共有10个。而据http://baike．so．com/doc/5534332．html网国外状况部分介绍“:组合数学在国外早已成为十分重要的学科,甚至可以说是计算机科学的基础。一些大公司,如IBM,ATamp;T都有全世界最强的组合研究中心。Microsoft 的Bill Gates近来也在提倡和支持计算机科学的基础研究。例如,Bell实验室的有关线性规划算法的实现,以及有关计算机网络的算法,由于有明显的商业价值,显然是没有对外公开的”。根据胡国定等编写的《简明数学词典》提及的10个组合数性质与恒等式进行比照,例(见参考文献[1])( ±)=(±)+(∓):

(1)组合数性质[帕斯卡公式(Pascal)]；

(2)组合恒等式(combinatirial identity)。

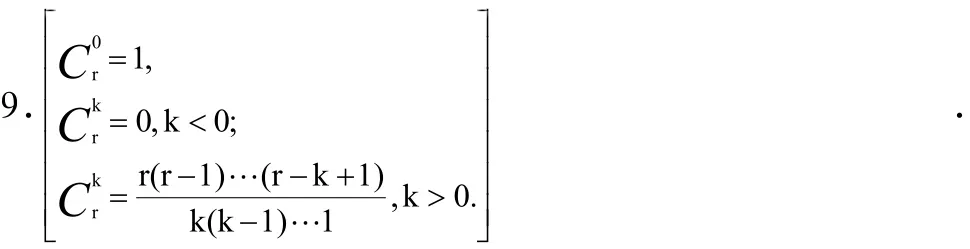
其中除5．6．8．9．中的部分外,大部分能在本文的移动运算中找到它们的存在之处。

鉴于此本文从任一行与紧邻下一行上或任一列与紧邻一侧列上的两点间的可产生的运算关系式类型,进行多种方向上的关系式类型的推导。产生新性质(含公式)94个,另含附类属公式181个合275个,预计产生应用公式3760个,总推得公式3854个,另有14处为原已存在的性质公式即原有恒等式(以下“结果值”一词简化用符号“※”表示)。

2 新三角形“△”内一行上的一般线性连贯关系

指完全一行上的前、后半数项之和与中项问题,及隔位项之和问题分两部分说明,存在性质(含公式)1～12合12个,其中新产生性质公式8个。

2.1 完全一行上的前、后半数项之和与中项问题

存在新产生性质(含公式)1～8合8个。

2.1.1 对于 (1+ 1)n形式

完全一行上的前、后半数项之和相等且都为2n-1,⑴．当n为偶数时,前、后半数项之和同加单一最中间项的一半,其值为2n-1；⑵．当n为奇数时,前、后半数项之和分别加前、后相等的两个最中间项,其值相等都为2n-1．存在新性质(含公式)1～2合2个。

⑴．当n为偶数时(共含奇数个项),前、后半数项之和同加单一最中间项的一半 1 /2时,其值为2n-1,见图2-4．性质,公式1；

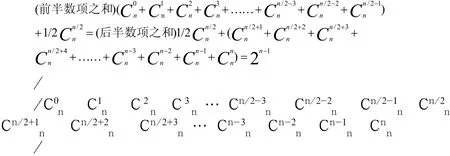
图2-4

⑵．当n为奇数时(共含偶数个项),前、后半数项之和分别加两个前、后相等的最中间项时,其值相等都为2n-1,见图2-5．性质

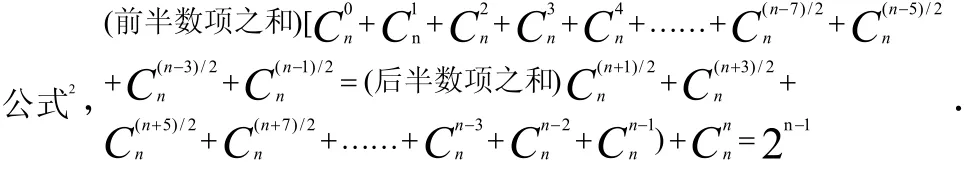
图2-5

2.1.2 对于 (1- 1)n形式

存在⑴．当n为偶数时,完全一行上的前、后半数项之和(同加本行单一最中间项)相等,其值为上一(奇数)行的同左斜列项即后一中间项[且n/2为偶数,即n≡mod(4,0)]或( -)[且n/2为奇数,即n≡mod(4,2)],且当n为偶数时,前、后半数项之和仅同加本行单一最中间项的一半,其和值为0；⑵．当n为奇数时(有前、后两个最中间项),前、后半数项之和互为相反数,其值为上一(偶数)行的同左斜列项即单一最中间项[且n为奇数,即(n-1)/2为偶数≡mod(4,2)]或[且n为奇数,即(n-1)/2为偶数≡mod(4, 0)]．存在新性质(含公式)3～8合6个。

下面分别叙述:(1)．当n为偶数时(共含奇数个项,仅含1个最中间项),(1)-①．且n/2为偶数,即n≡mod(4,0),见图2-6．因自上一行一端起与本行的连续运算(同加本行单一最中间项)的结果值等于上一行的同左或同右斜列项上的值,证明过程如下(以下此推导证明方式相同；故从略):

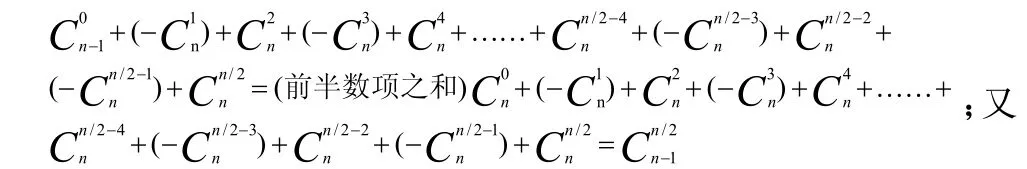
因其同一行上前、后半数项之和是相等的,所以(此处同加本行单一最中间项),其值为上一(奇数)行的同左斜列项即后一中间项

图2-6

⑴-②．且n/2为奇数,即n≡mod(4,2),见图2-6．前、后半数项之和相等[此处同加本行单一最中间项(-)],其值为上一(奇数)行的同左斜列项即后一中间项 (-),性质

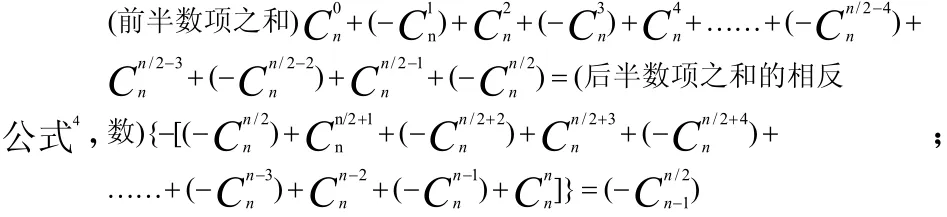
⑴-③．并n/2为偶数,即n≡mod(4,0),前、后半数项之和相等且仅同加本行单一最中间项的一半 1 /2,其和值为0,因同时符合了上一(奇数)行互为相反的前、后双中间项之和为0,性质

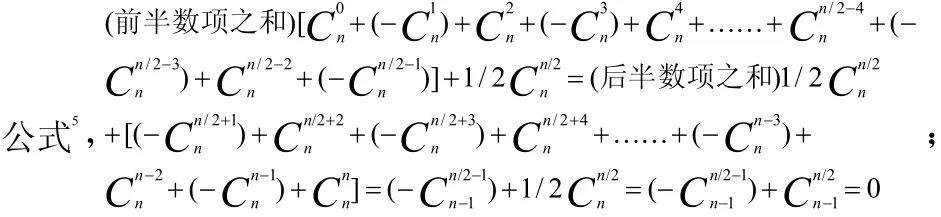
⑴-④．并n/2为奇数,即n≡mod(4,2),前、后半数项之和相等且仅同加单一最中间项的一半 1/2( -),其和值为0,因同时符合了上一(奇数)行互为相反的前、后双中间项与( -)之和为0,性质

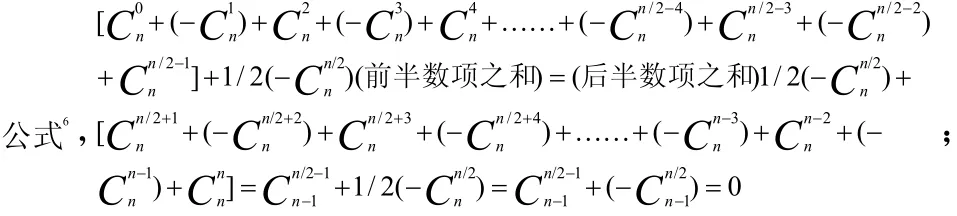
(2)当n为奇数时(共含偶数个项,有前、后两个最中间项),(2)-①．且(n-1)/2为偶数≡mod(4,2),前、后半数项之和互为相反数,其值为上一(偶数)行的同左斜列项即单一最中间项；(2)-②．且(n-1)/2为偶数≡mod(4,0),前、后半数项之和互为相反数,其值为上一(偶数)行的同左斜列项即单一最中间项见图2-7。

图2-7

⑵-①．并(n-1)/2为偶数≡mod(4,2),前、后半数项之和互为相反数{此处前、后分别加本行两个最中间项其值为上一(偶数)行的同左斜列项即单一最中间项C(n-1)/2,见图2-7．性质。

IKAnalyzer 是一个开源的基于Java 语言开发的轻量级的中文分词工具包，结合词典分词和文法分析算法，正向最大匹配，原则是有效文本长度越长、词元个数越少、路径跨度越大、歧义词词元队列位置越靠后、词元位置权重越大等。

（2)-②．并(n-1)/2为偶数≡mod(4,0),前、后半数项之和互为相反数{此处前、后分别加本行两个最中间项其值为上一(偶数)行的同左斜列项即单一最中间项 [- C(n-1)/2],见图2-7．性质。

2.2 完全一行上的隔位项之和问题

存在性质(含公式)9～12合4个,全为原已存在的性质公式。

2.2.1 对于 (1+ 1)n形式

完全一行上的偶、奇数位隔位项之和相等同为2n-1,存在性质(含公式)9～10合2个．得出2个性质(含公式)同属于原有恒等式。

⑴．当n为偶数时(共含奇数个项),偶、奇数位隔位项之和的值都为2n-1,参考见图2-4．性质公式9(此符合原已存在性质公式)(上标偶次项和)(上标奇次项和)即属原有恒等式n正整数。

⑵．当n为奇数时(共含偶数个项),偶、奇数位隔位项之和的值都为2n-1,参考见图2-5．性质公式10(此符合原已存在性质公式),(上标偶次项和即属原有恒等式n正整数．

(1）．当n为偶数时(共含奇数个项),参考见图2-6．偶、奇数位隔位项之和互为相反数,其值分别为2n-1、(-2n-1),性质公式11(此符合原已存在性质公式),

2.2.2 对于形式 (1- 1)n无论n为偶或奇数

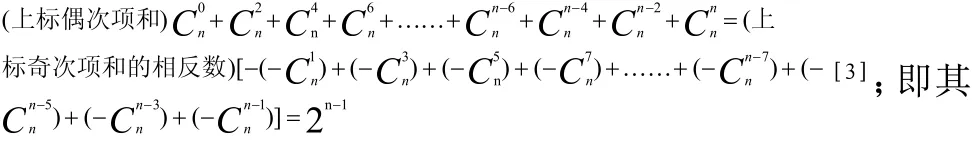
绝对值同属于原有恒等式

K=0K=0

⑵．当n为奇数时(共含偶数个项),参考见图2-7．偶、奇数位隔位项之和互为相反数,其值分别为2n-1、(-2n-1),性质公式12(此符合原已存在性质公式),

[1]胡国定等.简明数学词典,北京:科学出版社,2000,11:495.

[2]源流等.发散思维大课堂,高二代数(下)·试验本,北京:龙门书局出版社,2002,1:158.

王以将(1950—),男,农艺师,汉族,江苏阜宁人,毕业于江苏农学院.先后入编世界与国内优秀专家人才名典等.发表文章30余篇,获国际与国内优秀奖57项;涉及数列应用(农业类)的“植物分枝(蘖)的两种数学模型求解公式”一文在《中国科技财富》2009年第11期(下)登载.本文的前身是简要的《用滑动性六翼形区域解牛顿三角形之谜》,在2003年“第二届中国科学家”论坛上获二等奖.现经系统整理于下(全文约1200页).