论基于遗传算法的模拟电路优化设计方法

2014-12-10王泽华

中国科技纵横 2014年12期

关键词：电路设计适应度元件

王泽华

(湖南省长沙市中南大学,湖南长沙 410012)

论基于遗传算法的模拟电路优化设计方法

王泽华

(湖南省长沙市中南大学,湖南长沙 410012)

遗传算法可以有效解决电路优化设计面临的速度和规模瓶颈,虽然有固定的编解码方案,但是从结构设计角度看,电路优化的创造空间很大,影响参数可以满足适度调节需要。围绕遗传算法,设定的调节参数,其功能性很强,可以为元件控制设计、电路优化设计提供稳定的运算规范。基于此,本文将结合遗传算法相关内容,深度解析电路优化设计的若干问题。

遗传算法模拟电路优化设计研究方法

电路优化设计空间大,需挖掘的潜在空间很广。编辑模拟器作为电路的核心组件,其自动测试功能、运算功能、间接编码功能必须加速优化,只有这样,电路才能完成“与日俱增”的运算量。遗传算法可以利用放大器、过滤器、三极管等双端元件,适量简化电路的运算操作模式,使其能在标准运算的基础上,自动生成电路结构。

1 编解码方案与仿真技术

编解码是电路自动化设计的关键点,它直接参与到电路结构的构建工作。所以,根据遗传算法原理,编解码需设置多个节点,选择适当、合理的元件种类和个数,使自动生成的电路设计结构能够满足设计需要。同时,仿真技术也应适当升级、更新,因为以网表格为基础的电路结构,其二进制编码的设计需求和模式转型变化复杂,需依靠计算获得。电阻、电容等双端元件的编码计算公式为:

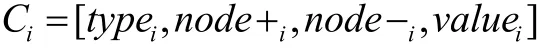
2 适应度评估方法

2.1 子目标集合

电路想满足多个运行要求,所以其电路结构中的运行目标是多样化的。在整合电路结构时,需利用遗传算法的子目标合成优势,转移信号,突显综合目标的主导优势,以顺利完成运算设计的适应度评估工作。

式中, wi表示电路适应度的权值系数,反映遗传算法的优化权重; Fit(X)i表示电路的各子运行目标,待X到达极限值时,子目标便可以统一规划适应度,形成标准的个体集合,集合中的每个参数都能表示电路设计目标。

2.2 权值系数的动态更新

因为遗传算法的标的值具有动态变化的特征,所以与人工神经网络工作原理相同,电路设计结构的权值系数也应随之变化,这样才能显现出电路与遗传算法的统一性和同步性。同时,权值系数的变化情况不是混乱的,是遵循一定规律的,如下:

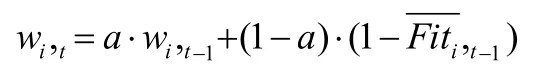
(0≤a≤常数)

2.3 频响曲线

遗传算法在计算响应频率时,幅度-时间曲线是随着电路设计结构的变化而变化的,个体的电路特性,其运算量仿真效果不明显、不理性、不规范。为此,要想降低误差,使个体适应度能够高度吻合电路设计结构,遗传算法必须利用频响曲线,丰富设计功能。简化公式为:

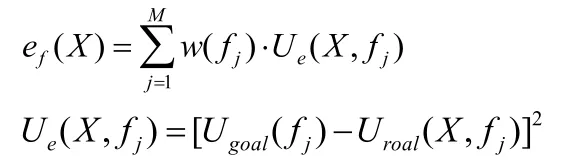
式中, fj表示电路设计频率采样位置;表示理想状态下,遗传算法计算出来的频响特性表示电路实际运行状态下的仿真效果。

3 遗传参数调整策略

通过上文分析可知,遗传算法在电路设计中各参量值、权值系数计算上起到了很强的影响作用,在没有确定交叉概率之前,Pc和变异概率对电路设计的影响也很大。为此,要防止电路低能粗略搜索,影响结构稳定,需适当调整遗传参数,并根据其变化情况,分析整体电路设计的优化策略,具体内容如下。

3.1 确定基因段的取值范围

因为电路中染色体对子目标的控制能力有限,所以染色体中的基因段很难测试出遗传参数的变化范围。如果电路的遗传进程被改变,则电路的响应功能会立即崩溃,相应元件的功能性也会随即减弱。由此可见,遗传参数调整策略的首要前提是,优化内容需根据基因段的取值范围,测算元件类型、遗传进程、遗传参数变化等内容。

3.2 电路结构、类型的统一设定

除基因段之外,电路的结构类型也会干扰遗传算法的准确度,在高位序基因段中,电路子目标所体现的权值系数根本无法解决结构差异问题,也无法满足调节遗传参数系数的运行要求。因此,电路优化设计需采用“先定结构,后定参数”的设计模式,在排除个体适应度影响的基础上,合理分配电路各设计层的工作任务和设计要求,尽可能做到“共同决定”。同时,如果调整后的遗传参数仍不能满足电路正常运行,则应从电路设计入手,根据信号响应力差异,缩短检索范围,增强遗传进程的主导能力,提高遗传运算量。

3.3 增进遗传参数的相互配合

因为遗传运算进化中隐含多个电路结构,其设计参数、结构变化区段、系数取值范围各不相同,为连接不同阶段的层级电路,需利用遗传参数的交叉概率、变异概率,测算电路拓扑结构的影响范围,并确定元件类型。如果支撑电路的元件、遗传参数、电路规模无法满足适应度,深受其他设计要素影响,则需在保持电路基本设计结构的基础上,调节各元件参数。