有限温度电子星
2014-12-08范金帛曾定方
范金帛 曾定方
(北京工业大学,北京 100124)
有限温度电子星
范金帛 曾定方
(北京工业大学,北京 100124)
考虑一个在 3+1d 全息时空中电磁场,引力场与带电费米子相互作用的模型,与 Hartnoll, Petrov 所建立的模型[1]不同,我们考虑了hawking效应,认为这些带电粒子满足有限温度的热力学分布。通过计算,我们发现这样的模型,其带电粒子n,ρ,p分布呈壳层结构,且运动方程组不允许一个极端黑洞解的出现,这可作为弱引力猜测的一个例子。
电子星 弱引力猜测
凝聚态理论当前面临的一个挑战是,在2+1d时空中有限密度费米子与无能隙的玻色激发(自选密度波,临界规范场)是如何相互作用的[2][3][4]。这种强相互作用无法通过微扰论所描述,而AdS/CFT恰能提供一种强/弱对偶的技术手段[5][6][7],我们只需要去考虑在一个弱弯曲时空背景下的引力理论即可。在这篇文章中,我们基于[8]考虑了电磁场,带电米费米子对引力场的反作用,且这些带电费米子是满足有限热力学分布的。
1 运动方程和时空背景
我们没有依照作用量原理的观点,而直接从运动方程的角度出发。有一个负宇宙学常数和源的Einstein-Maxwell运动方程如下
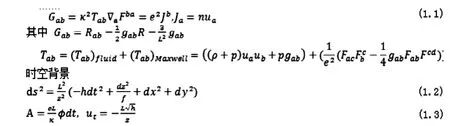
上述的 Einstein-Maxwell运动方程可以表示为如下的4个运动方程
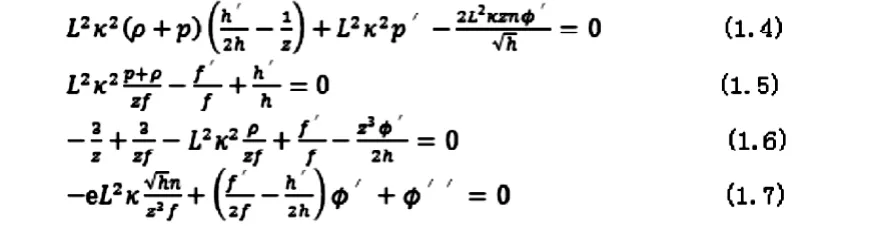
2 运动方程的解
带电费米子满足有限温度的热力学分布

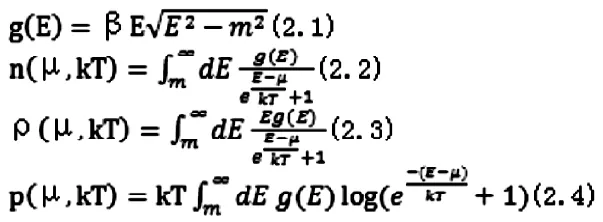
使用热力学关系和化学势在平直时空中的表示

我们发现如果,式(1.4)与(2.5)等价。即说明,Einstein-Maxwell方程会给予有限温度的热力学第一定律。
新的运动方程组为
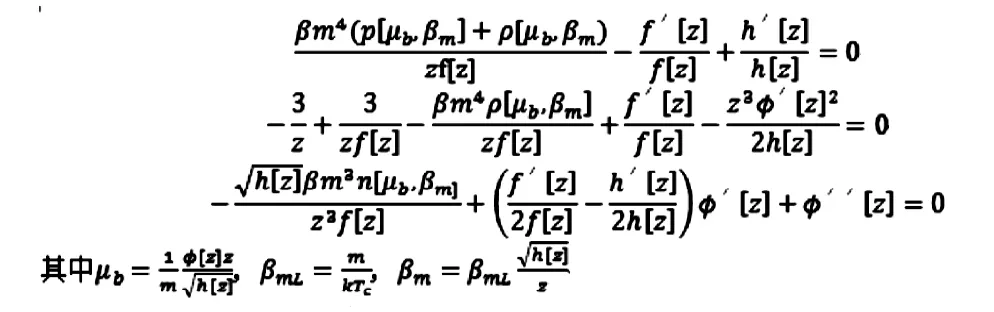
从更方便的技术角度讲,我们选择合适的边界条件从星体外部积分向星体内部。对于外部的观察者,电子星相当于一个RN黑洞,故,假定边界条件为
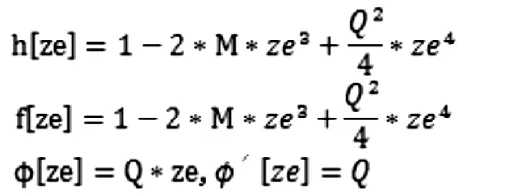
通过mathematica数值计算,我们发现
3 结语
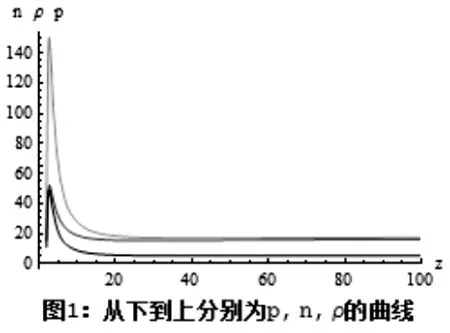
在零温电子星的情形中[8],n,ρ,p的分布星体中心处渐进平坦。比较图1,我们发现有限温度电子n,ρ,p的分布呈壳层结构。图2表示,当固定了m,β,M,Q,降低特征温度时,粒子束密度尖锐的峰形会渐渐消失,当的时候,n的分布图自然过渡到零温情形下。这是因为例子的热运动越演平缓,离子束密度分布的壳层结构越发不明显。整个计算过程中,我们都是在经典引力区域进行。如果弱引力猜测[9]是正确的,0<m<1,我们发现上述的运动方程组没有一个黑洞解。即这样的电子星并不能形成极端黑洞。
[1]Sean.A.Hartnoll andPavelPetrov.arXiv:1011.6469.
[2]Ar.Abanov and A.Chubukov, Phys.Rev.Lett.84.5608(2000).
[3]Ar.Abanov and A.Chubukov, Phy.Rev.Lett 93.255702(2004).
[4]M.A.Metlitski and S.Sachdev, arXiv:1005.1288[cond-mat.strel].
[5]J.Maldacena, Adv.Theor.Math.Phys.2(1988)231-252,[hep-th/9711200].
[6]S.Gubser,I.Klebanov and A.Polyakov,Phys.Lett.B428(1988)105-144,[hep-th/9802109].
[7]E.Witten, Adv.Theor.Math.Phys.2(1988)253-291,[hep-th/9802150].
[8]Sean A.Hartnoll and AlirezaTavanfar, arXiv:10082828.
[9]NimaArkani-Hamed, LubosMotl, Alberto NIcolis and CumrunVafa.Jhep06060(2007).
