论模具球面加工

杨省缺

(河北省科技工程学校,河北保定 071000)

论模具球面加工

杨省缺

(河北省科技工程学校,河北保定 071000)

本文针对模具类工件的球面加工提出了选用数控机床、采用标准刀具、利用宏程序可变量赋值、可循环、可跳转等功能。选用标准平底及球头刀具完成各种球面加工,大大降低了生产成本,提高了球面加工精度及效率。

球面加工 宏程序 螺旋运动加工

球面包括外凸、内凹球面，常见于各种模具，无论是热锻模、冲压模、拉伸模、注塑模均等均属于常用加工内容。其绝大多数属于单件、小批量生产类型，难以采用专用刀具及专用机床等方案，通常的加工方法为三维螺旋加工法，在加工中心或数控铣床上，依据球体数学模型，确定各要素之间的逻辑关系式，然后给相对应的变量赋值，利用宏程序可变量赋值、可循环、可跳转等功能，选用球头铣刀结合平底铣刀完成球面加工。无论是加工效率还是加工精度，都堪称当前制造业最佳方案。本文拟就对不同层面的球面加工中确定数学模型及逻辑关系、加工工艺及刀具选择以及各项加工参数确定、宏程序的编制等问题进行探讨。

1 数学模型及技术分析

1.1 半球体

1.1.1 凸半球体

如图1所示，此工件为凸半球体，加工这一球面体时，可依据勾股定理建立数学模型，确定各要素之间逻辑关系根据加工要求设置变量并给变量赋值。

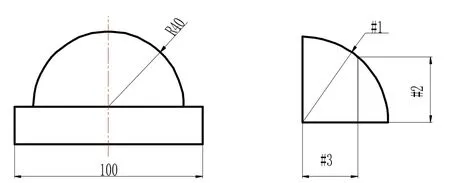
图1

如图1所示各项参数的设定及说明如下：

其中：

#1=40为球体半径。

#2=0为Z向以球心为起点的初始值。自下而上加工球体时为每一次循环Z向加工向上递增的变量值，据加工面精度要求给#2赋值，一般为0.05～0.1mm。

#3=SQRT[#1×#1-#2×#2]为X方向变量值，初始值为#1，依据上述数学逻辑关系，加工过程中逐步递减，当#2逐步递增到40时#3=0。

1.1.2 凹半球体

如图2所示，此工件为内凹半球体，其数学模型、相对逻辑关系、变量与赋值，基本参照图1外凸球体，所不同的是所选刀具为球头铣刀，循环变量为角度，加工方案自上而下。

如图3所示各项参数的设定及说明如下：

#1=40 为球体半径

#2=6 为球刀半径

#4=0 为角度变量初始值。自上而下加工球体时为每一次循环#4 加上递增的变量值，根据加工面精度要求给#4赋值，一般为0.5°左右。

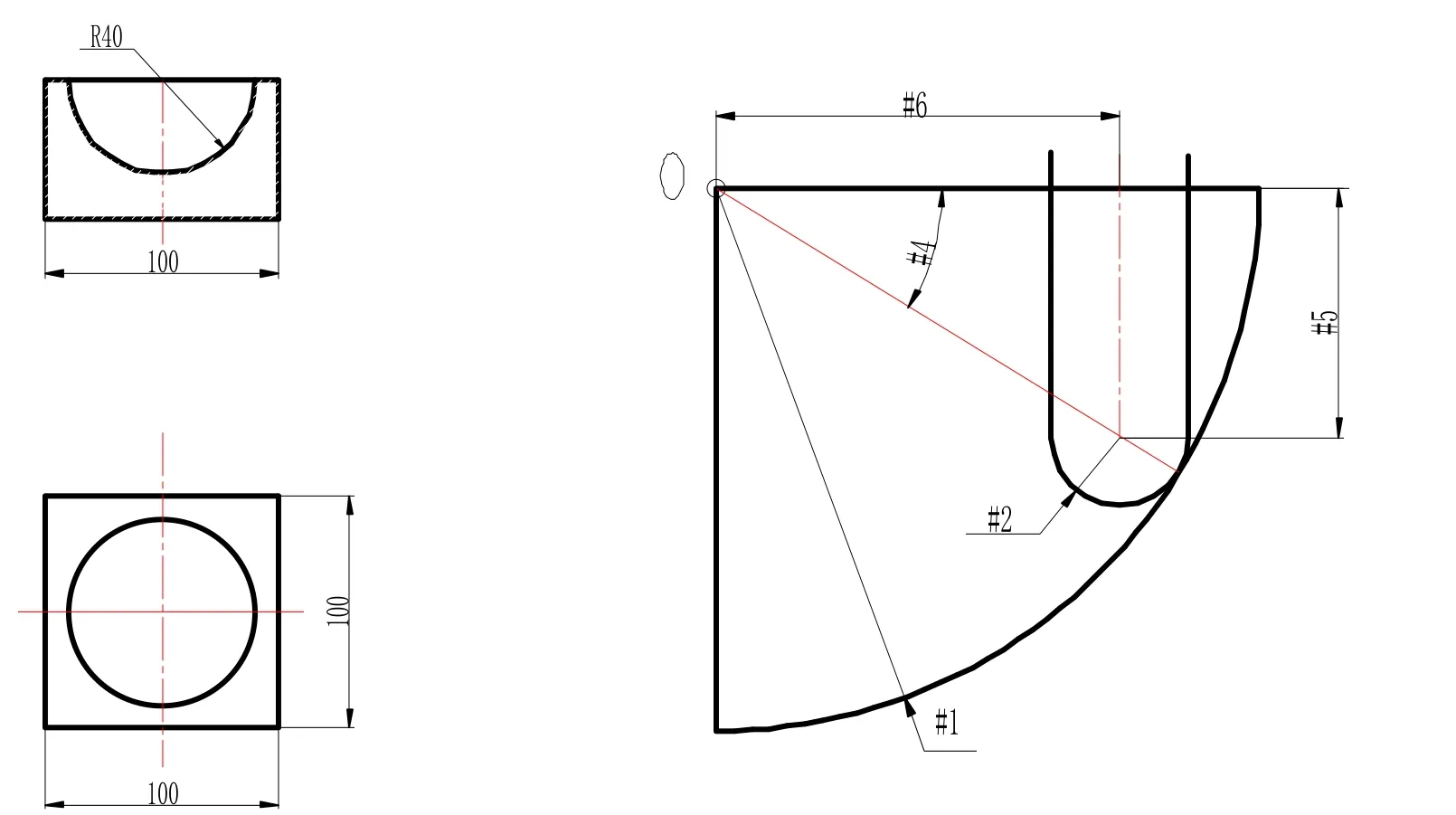
图2

#5=[#1-#2]×SIN[#4]为加工过程中球刀刀心轨迹的Z方向变量值，初始值#4=0时，#5=[#1-#2]×SIN[#4]=0

#6=[#1-#2]×COS[#4]为加工过程中球刀刀心轨迹的X方向变量值。初始值#4=0时，#6=[#1-#2]×COS[#4]=#1-#2=34

1.2 球缺

2.1.1 凸球缺

如图3所示：

#1=40 球体半径

#2=15 球体Z方向相对于球心起点，初始值为15

#3=SQRT[#1×#1-#2×#2] 为X向变量值，并依函数关系当#2逐层递加时，#3逐层递减，当#2等于40时，#3等于零。

2.1.2 凹球缺

如图4所示：

#1=40 球体半径

#2=6 球头刀具半径

#3=30； 铣削球面的深度赋值

#4=ASIN [[#1-#3]/#1]： 角度变量赋初始值

#5=[#1-#2]×SIN[#4]； 定义球刀刀心轨迹的Z向变量值

#6=[#1-#2]×COS[#4]；定义球刀刀心轨迹的X向变量值

#5、#6分别为球刀刀心Z向、X向变量值，依函数关系当#4逐层递加时，#6逐层递减，当#4等于90时，#6等于零。

2 加工程序及工艺过程说明

2.1 凸半球体加工程序

O0001(程序名) 已粗加工完毕，自下向上只精加工球体。

N10 G90 M03 S1000；绝对坐标编程，主轴正转每分钟1000转

N20 G00 G54 X0 YO Z100； 建立坐标系，以球心为原点，设Z轴安全高度100

N30 #1=40； 球面半径赋值

N40 #2=0； Z向高度起始点赋值

N50 X80； 选用Φ 20立铣刀，X正向快速定位

N60 Z5； Z向快速下刀

N70 G01 Z#2 F50； Z轴下刀至球心，Z向零点位置

N80 G01 X#1 F200；X向切入，初始值为球面半径值，建刀补

N90 #3=SQRT[#1×#1-#2×#2]； 定义X向变量值

N100 G02 X#3 Z#2 I-#3； 自下而上螺旋加工

N110 #2=#2+0.1； Z向累加递增赋值，根据精度要求调整

N120 IF[#2LE40]GOTO 90 ； 判断语句当#2小于等于40时，无条件转移到N90语句循环加工

N130 G01 XO YO； 结束循环

N140 GOO Z100； 抬刀至安全高度

N150 M30； 程序结束，返回程序头

注意：对刀时注意Z轴零点在圆弧的球心，而不是上表面。N50句的X80与圆弧半径和刀具半径有关。

图3

图4

2.2 内凹半球体加工程序

O1900(程序名)

N10 G90 M03 S1000； 绝对坐标编程，主轴正转每分钟1000转

N20 G00 G54 XO YO Z100；建立坐标系，以球心为原点，设Z轴安全高度100

N40 #1=40； 球面半径赋值

N50 #2=6； 刀具半径赋值

N60 #4=0； 角度变量初始值

N70 G01 X[#1-#2] YO F200 M08； 移动刀具到下刀点

N80 G01 Z#4 F50； 以切削进给速度Z轴下刀

N90 #5=[#1-#2]×SIN[#4]； 定义球刀刀心的Z向变量值

N100 #6=[#1-#2]×COS[#4]； 定义球刀刀心的X向变量值

N110 G02 X[#6]YO I[-#6]Z[-#5]； 自上而下螺旋加工

N120 #4=#4+0.5； 变量累加赋值，可根据精度要求调整

N130 IF[#4 LF 90] GOTO 90； 判断语句当#4小于90时，转移到N90语句循环加工

N140 G01 XO YO； 螺旋加工完毕，为Z向抬刀做准备，因FANUC系统圆弧插补语句不能快速抬刀

N150 GOO Z100； 快速抬刀

N160 M3O； 程序结束，返回程序头

2.3 凸球缺加工程序

可参照凸半球体加工程序将Z向变量#2的赋值加以修改，如图3所示：#2=40-25=15，调整N80句中X#1为X[SQRT[#1×#1-#2×#2]]。

3 结语

本文所提供的程序为螺旋加工，过程连续流畅，无停顿现象，加工精度高。

以上程序均在FANUC 0i系统上运行过，只需做适当调整，即可用于各类球面加工。今总结与此，此期与同行交流。

杨省缺,女,出生于1965年9月18日。籍贯:河北省石家庄市无极县,1988年毕业于河北轻化工学院机械系,现于河北保定市河北省科技工程学校机械系任教。