基于距平分析的Argo海表温度场重构

王文娟，俞胜宾，杨凡，刘增宏

(1.国家海洋局南海预报中心，广东广州510310；2.国家海洋局第二海洋研究所，卫星海洋环境动力学国家重点实验室，浙江杭州310012；3.国家海洋局珠海海洋环境监测中心站，广东珠海519015)

1 引言

Argo 计划首先在1999年召开的海洋观测大会上提出，旨在快速、准确、大范围地收集全球海洋上层的海水温、盐度剖面资料，以提高气候预报的精度，有效防御全球日益严重的气候灾害给人类造成的威胁，被誉为“海洋观测手段的一场革命”。Argo观测数据已成为目前获取海洋的气候状态信息的主要来源，被广泛应用到物理海洋学及气候学的多个领域中，内容涉及海-气相互作用、海洋环流、厄尔尼诺、中尺度涡、水团性质及变化等。

每年海量增加的Argo 剖面观测数据在很大程度上弥补了过去海洋观测资料匮乏的不足，但是由于该资料具有时空分布不规则的缺点，仅研究该资料本身还远远不能发挥Argo 数据的应用潜力，因此，有必要借助于数据同化技术，将其单独或结合常规温、盐度观测数据进行网格化。为此，许多国际Argo成员国已经在尝试开发针对Argo数据的网格化产品，如：法国海洋开发研究所Coriolis中心设计开发了基于最优插值技术的ISAS(In Situ analysis system)温盐分析系统[1-3]；美国Scripps 海洋研究所的Rommich 等[4]利用最优插值法，将2004—2008年期间全球海洋上的Argo 资料建成为逐年逐月的海温、盐度网格资料产品；日本气象局首次实现了全球温盐图的常规化制作[5]；英国气象局[6]、印度海洋信息中心[7]则基于Gauss-Markov原理的客观分析法，构建了印度洋海域的Argo网格资料等。近年来，我国学者在Argo数据重构领域也做了大量探索性研究。张韧、黄志松等[8]采用时空权重插值和多变量DINEOF 方法，对太平洋区域2000年1月至2008年12月的三维逐周盐度场进行重构。刘巍、张韧等[9]提出一种分形插值的改进算法，用遗传算法对分形插值模型的垂直压缩参数进行了优化选择，并进行了Argo 海温资料插值加密的对比试验。张春玲、王振峰等[10]利用最优插值数据同化方法对Argo资料进行了网格化实验。李宏、许建平等[11]利用逐步订正法构建了2002年1月至2009年12月期间太平洋海域的逐月温、盐度网格资料。杨胜龙、马军杰等[12]采用Kriging算法，将2007年1—12月份期间获得的太平洋海域的Argo 剖面浮标资料重新构成3°×3°的月平均海温场。

以上研究大多直接分析Argo 观测数据，对Argo 数据稀疏的海域往往不能取得理想的效果。本文拟建立一种基于距平分析的Argo 数据重构方法，即首先计算Argo观测点的海表温度（SST）距平值，然后利用Kriging 插值获取网格化距平场，再叠加气候态平均SST，重构水平分辨率1°×1°的印度洋海温分布。

2 资料来源与处理方法

2.1 资料来源

选取中国Argo 实时资料中心提供的2003年8月和2012年8月Argo 温盐剖面浮标资料（海域范围：60°S—30°N，25°—125°E）作为Argo温度场重构的原始散点数据，这些资料均已经过各国Argo资料中心的实时和延时资料控制，通过Akima插值形成表层采样点海水温度。

选取NOAA 提供的最优插值海面温度场(OISST V2.0)作为“实际海温场”对Argo重构数据进行验证。OISST V2.0 是通过最优插值方法将站点观测资料和卫星遥感SST 资料进行同化分析得到的空间分辨率为1°×1°的逐月全球再分析数据集，其中卫星遥感SST数据已经过雷诺法矫正其偏差[13-14]。

2.2 Argo数据重构方法

利用OISST V2.0 数据生成1982—2012年8月份气候态SST数据场，经过线性插值方法提取Argo浮标采样点处历史平均温度其中N为该月份Argo 观测样本数量），Argo 浮标观测温度为Ti，则该处海温距平值为：

对样本距平序列进行Kriging插值，得到待求海域的海温距平场d，则待求海域的海表温度场估计值为：

2.3 Kriging插值

Kriging插值是地统计学的主要方法之一，它是法国地理数学家Georges Matheron和南非矿业工程师D·G·Krige发明一项实用空间估计技术，目前已被广泛应用于矿产储量计算、遥感数据处理、地质学、水文学、环境科学、农林科学和农田水利等诸多方面。其插值实质是利用区域化变量的原始数据和变异函数的结构特点，对未采样点的区域化变量的取值进行线性无偏、最优估计。Kriging方法通过引进以距离为自变量的半变差函数来计算权值，由于半变差函数既可以反应变量的空间结构特性，又可以反映变量的随机分布特性，利用该方法进行空间数据插值往往可以取得理想的效果。另外，通过设计变差函数，Kriging方法很容易实现局部加权插值，克服了一般距离加权插值结果的不稳定性[15-17]。

设Z(x,y)是承载的区域变化量，并且满足二阶平稳假设（或本征假设），定义在点(xi,yi) 上的Zi(i=1,2,…,n)是一组离散样本数据，则对点(x0,y0)承载处的区域化变量进行估计，所用的估计量为[15]：

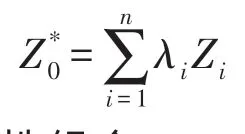
它是n 个数值线性组合。Kriging 方法的原则是在保证这个估计量无偏并且估计方差最小的前提下，求出n 个权值系数λi。根据上述条件建立Kriging方程组：

式中，N( h )是被向量h相隔的数据对的个数。

2.4 验证方案

由于Argo浮标观测点处OISST值与Argo观测值存在偏差，有些地方相差甚至超过1 ℃，因此，采取下述方案进行重构方法的验证：（1）提取对应月份Argo 观测点位置信息(xi,yi) ；（2）通过线性插值方法获取该月份OISST在(xi,yi)处的海表温度Ti；（3）通过线性插值方法获取气候态SST 在(xi,yi)处的温度值（4）计 算(xi,yi)处的距平值（5）对距平值序列di利用Kriging 插值，计算整个海域的距平场d；（6）利用公式重构OISST 海温场；（7）计算OISST 海温场T 与重构OISST海温场T^ 的均方根误差及平均相对误差。

3 Argo数据重构结果分析

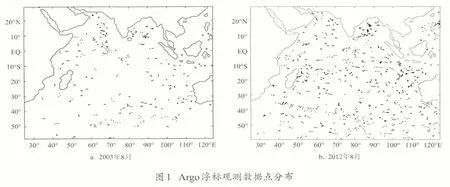
利用不同重构方法分别对2003年8月份和2012年8月份海域利用Argo观测数据进行网格化，最终生成1°×1°的海温场数据。其中2003年8月计算海域Argo 浮标观测数据为530 个，2012年8月Argo 浮标观测数据为1236 个，其分布如图1 所示。早期Argo浮标数量偏少且分布很不均匀，而后期随着Argo观测计划的深入开展，浮标海量增加。

3.1 Kriging插值重构结果分析

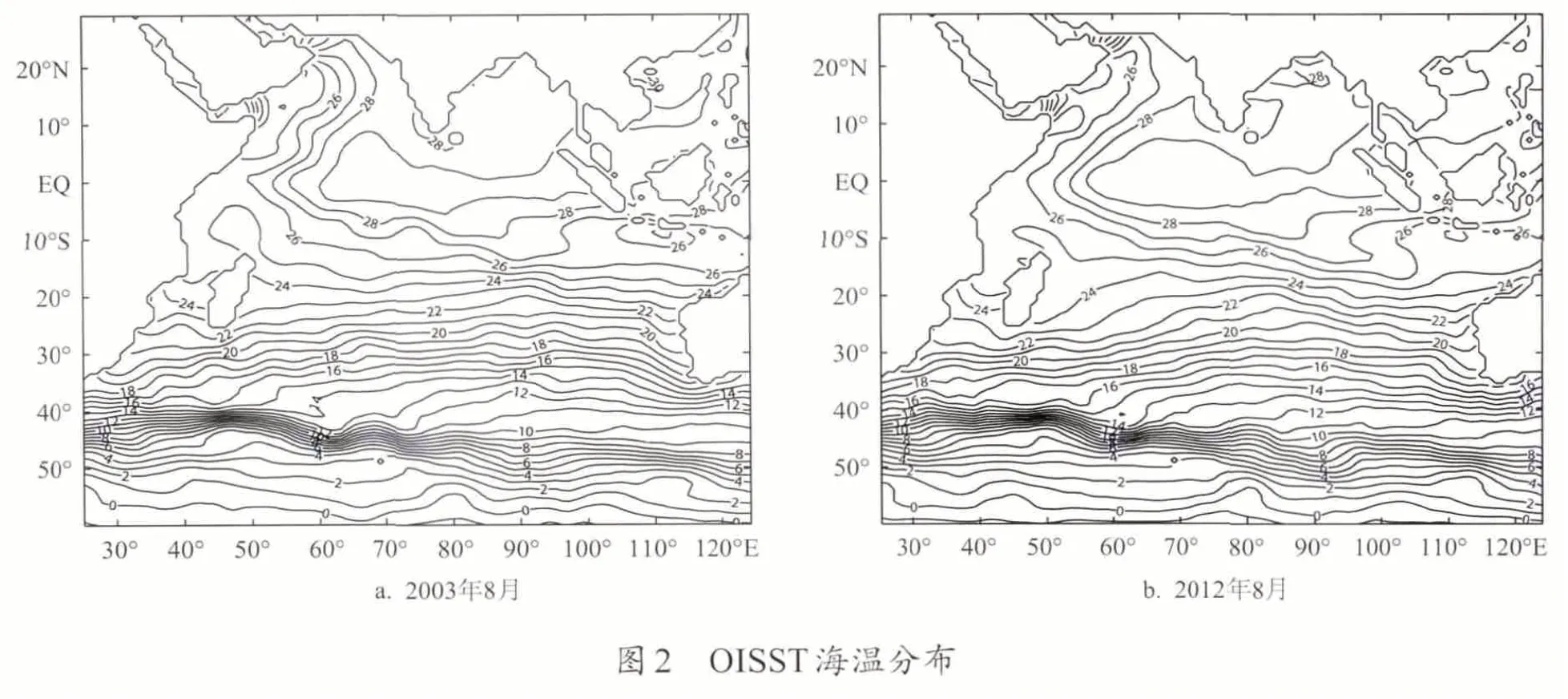
图2 是OISST V2.0 在2003年8月 及2012年8月海表温度水平分布图，可以看出，除阿拉伯海西北部以外，印度洋10°S以北海域的SST主要特征表现为一个暖池，10°S以南海域的等温线大致与纬线平行，且有较强的经向梯度。

图3 为直接利用Kriging 方法对Argo 数据进行插值后生成的海表温度分布图。对比图2和图3可以看出，对样本数据数量较多的2012年8月，Kriging 方法能够较为准确地重构出印度洋海域的温度场分布，尤其位于热带东印度洋的暖水区等温线吻合较好，位于40°—50°S 附近的极锋也有较好表现，但在50°S 以南的边缘海域，等值线走向发生改变，与OISST数据有较大偏差。而对数据较为稀疏的2003年8月，本方法得到的海温场在40°S以北的印度洋海域与实况也较为吻合，但在40°S以南的南大洋则表现出较大的偏差，极锋表现不明显，纬向分布的等温线在边缘转为经向。

3.2 基于距平分析的重构结果分析

图4 为采用2.2 节基于距平分析的方法建立的Argo海温场数据，两个月份的重构海温场与OISST数据均具有高度的一致性。其中2003年8月位于40°—50°S 附近的极锋和实况十分接近，50°S 以南的等温线分布也呈现和OISST 一致的纬向分布特征，2012年8月海域南侧边缘等温线分布也得到很好的修正。重构的2012年8月海温场在73°E 以东的南大洋出现较大波动，对该区域Argo数据分析显示，重构的海温场等值线与Argo数据具有更高的一致性，即重构数据在Argo浮标附近保留了更多的海温分布细节。对OISST与重构数据进行合成（见图5），显示重构海温场与OISST等温线分布具有较高的吻合度。

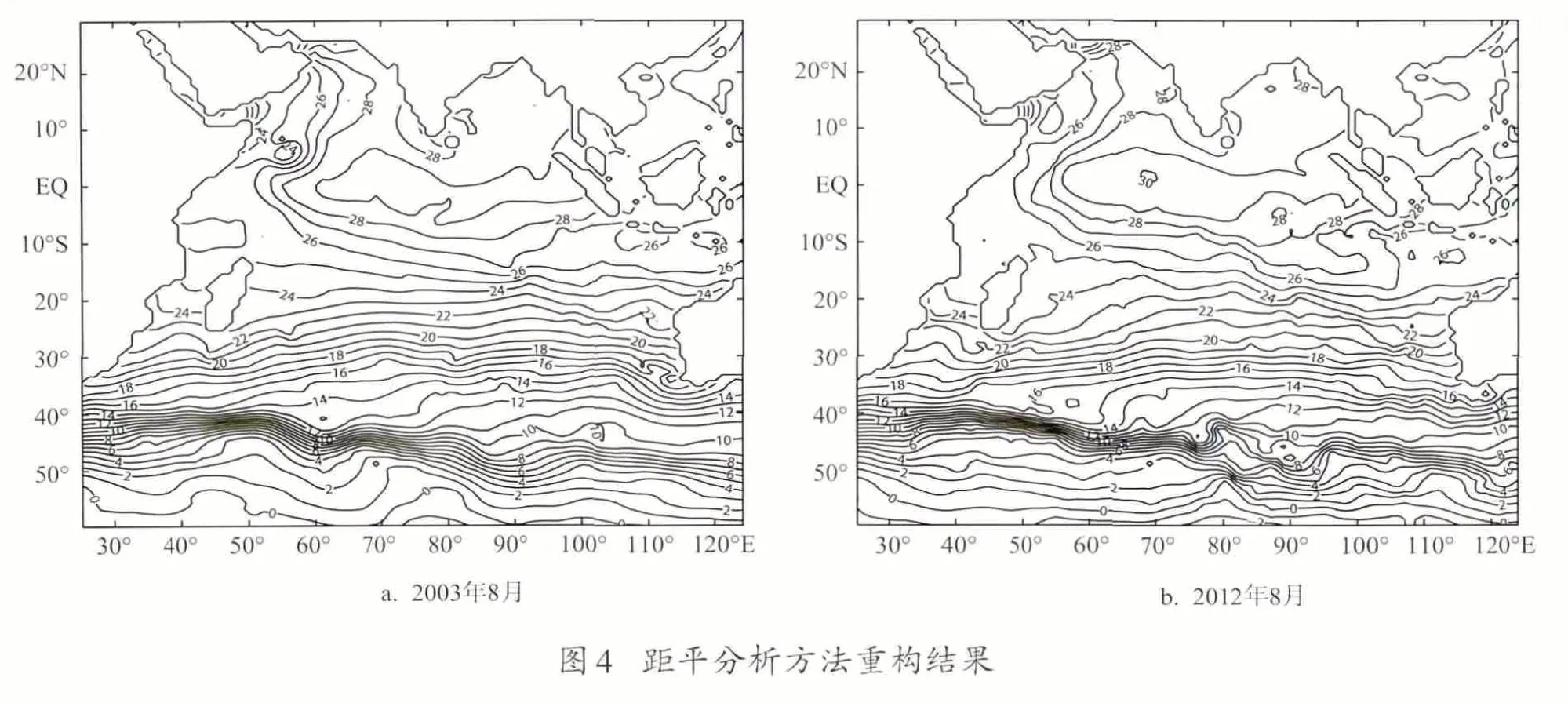
对比图3和图4，可以看出基于距平分析重构的Argo海表温度场比直接Kriging插值得到的Argo海表温度场能够更为准确地描述实际温度场分布特征。

图5 OISST原始场与距平分析重构场对比（实线为O IS S T 原始场）

利用2.4 节介绍的验证方案进行基于距平分析的重构方法的验证。假设OISST 为真实的海温场分布，用Argo浮标观测点位置的OISST海温值代替Argo观测值，利用距平分析的方法重构OISST海温场并与OISST 原始场进行对比分析。分别对2003年8月和2012年8月进行验证分析。观测数据较多的2012年8月均方根误差和平均绝对误差分别为0.18 ℃和0.12 ℃，观测数据较少的2003年8月均方根误差也仅为0.24 ℃，平均绝对误差为0.17 ℃。

4 结论

随着Argo 剖面浮标的海量增加，Argo 数据已成为获取全球海洋温盐资料的重要来源之一。对散乱的Argo 资料进行网格化重构是进一步分析温盐时空分布特征、研究气候变化、海气相互作用及数值模拟的基本要求。

本文分别对2003年8月和2012年8月的Argo浮标数据提取距平序列后进行Kriging 插值并叠加气候态SST海温场重构印度洋表层海温场，结果表明：（1）这种基于距平分析方法重构的温度场较Argo数据直接Kriging插值的结果在精度上有大幅提高；（2）重构的温度场与OISST V2.0 海温场的等温线具有高度的一致性，并且在Argo浮标附近海域有更好的细节表现；（3）即使在Argo 数据相对稀少的海域，基于距平分析方法重构的海温场也能保持较高的精度要求，包括在边缘海域和南大洋极锋附近均有较好表现。

本文提出的基于距平分析的Argo 数据重构方法物理意义清晰，计算简单，并能够取得较为满意的效果。该方法能够将Argo 资料与再分析数据有效结合，获取更为准确的Argo 网格化数据，弥补Argo观测资料信息的不足。

[1]Charraudeau R, Gaillard F. ISAS_V4: Mise en place de la configuration[R].Rapport LPO 07-09,2007.

[2]Gaillard F, Charraudeau R. ISAS_V4.1b: Description of the method and user manual[R].Rapport LPO 08-03,2008.

[3]Gaillard F. ISAS-Tool Version 5.3: Method and configuration[R].Laboratoire de Physique de Océans,UMR 6523,2009.

[4]RoemmichD, Gilson J. The 2004-2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the Argo Program[J].Progress in Oceanography,2009,82(2):81-100.

[5]HosodaS, OhiraT, NakamuraT. A monthly mean dataset of global oceanic temperature and salinity derived from Argo float observations[J].JAMSTEC RepResDev,2008,8:47-59.

[6]Martin M J, Hines A, Bell M J. Data assimilation in the FOAM operational short-range ocean forecastingsystem: a description of the scheme and its impact[J]. Quarterly Journal of the Royal Meteorological Society,2007,133(625):981-995.

[7]UdayaBTVS,RacichandranM,Devender M R,et al.An operational Objective Analysis system at INCOIS for generation of Argo Value Added Products[R].Technical Report,2007.

[8]张韧,黄志松,王辉赞,等.基于Argo资料的三维盐度场网格化产品重构[J].解放军理工大学学报(自然科学版),2012,13(3):342-348.

[9]刘巍,张韧,王辉赞,等.分形插值参数的遗传优化及其ARGO海温场应用试验[J].大气科学学报,2010,33(2):186-192.

[10]张春玲,王振峰,李宏.基于最优插值法的Argo数据网格化实验[J].海洋测绘,2012,32(3):29-31.

[11]李宏,许建平,刘增宏,等.利用逐步订正法构建Argo 网格资料集的研究[J].海洋通报,2012,31(5):502-514.

[12]杨胜龙,马军杰,伍玉梅,等.基于Kriging方法Argo数据重构太平洋温度场研究[J].海洋渔业,2008,30(1):13-18.

[13]Reynolds RW, Rayner NA, Smith T M, et al.An improved in situ and satellite SST analysis for climate[J]. Journal of Climate,2002,15(13):1609-1625.

[14]Smith TM,Reynolds RW. A high-resolution global sea surfacetemperature climatology for the 1961-90 base period[J]. Journal of Climate,1998,11(12):3320-3323.

[15]王靖波,潘懋,张绪定.基于Kriging 方法的空间散乱点插值[J].计算机辅助设计与图形学学报,1999,11(6):525-529.

[16]申静,苏天赟,王国宇,等.基于Kriging算法的海底地形插值设计与实现[J].海洋科学,2012,36(5):24-28.

[17]李晓军,王长虹,朱合华.Kriging插值方法在地层模型生成中的应用[J].岩土力学,2009,30(1):157-162.