行星齿轮传动系统齿面修形研究
2014-12-05王志国邱兰菊余晓辉
王志国,邱兰菊,余晓辉,汤 鱼
(1.绥化学院,黑龙江 绥化152000;2.宿迁泽达职业技术学院,江苏 宿迁223800;3.中国船舶重工集团公司 第七〇三研究所,黑龙江 哈尔滨150036)
0 引 言
渐开线齿轮在空载工况下,能够保证啮合齿对的共轭运动,实现平稳传动。实际齿轮传动过程中,齿轮总是处于单数齿对和双数齿对交替进行啮合,因齿轮自身存在制造误差及在载荷作用下会产生弹性变形,这使得齿轮在啮合过程中产生啮入啮出冲击。在受载齿轮传动系统中,轴、轴承、箱体等部件将会产生变形,导致轮齿的螺旋线发生改变,致使轮齿沿齿宽方向产生边缘接触,造成载荷沿齿宽方向分布不均,产生偏载现象[1]。为了改善啮合区载荷分布情况及啮入啮出冲击,提出了很多改善方法,齿轮修形被认为是最直接、最经济的方法。合理选择轮齿修形参数能够提高轮齿的承载能力、改善啮合区的载荷分布、提高传动的平稳性以及降低传动过程中产生的振动和噪声。本文通过对行星齿轮传动系统进行齿面修形研究,分析齿面修形对行星齿轮传动系统动态特性的影响,其中包括对传动系统内部激励(刚度激励、误差激励、啮合冲击激励)的影响以及对齿轮传动系统动态啮合力的影响。
1 齿轮修形目的
齿轮在相互啮合过程中,想要实现传递运动的平稳性,首先应该保证主被动轮齿上的基节处处相等,但由于齿轮在带载运行过程中会发生轮齿弹性变形,致使主被动轮齿上的基节不能相等,导致轮齿之间的干涉现象,从而会出现轮齿之间的啮入和啮出冲击,导致齿面载荷分布不均,严重降低齿轮的使用时间。为了能够改善轮齿啮入啮出冲击现象,一般利用齿面修形的方法,轮齿齿面修形一般分为齿廓和齿向修形2 种。齿廓修形是指在齿轮齿顶或齿根沿着齿面法向去除一定材料的方法,齿廓修形能够有效改善齿轮啮入啮出冲击;齿向修形一般是指沿着齿宽的方向去除一定材料的方法,齿向修形在斜齿轮以及齿宽比较大的情况下应用较多,齿向修形能够有效改善齿面载荷分布,减少齿面载荷集中,防止齿面点蚀和胶合。本文是关于行星齿轮传动系统的修形设计,齿轮采用渐开线斜齿轮,因为齿轮齿面较宽,因此在对行星齿轮传动系统进行修形设计时,同时对齿面进行齿廓和齿向修形的三维修形方法。
2 齿廓修形参数
2.1 修形量的确定
齿廓修形量指在齿顶和齿根上沿齿廓法线方向去除材料的多少。齿廓修形量根据齿轮在啮合点的综合变形和齿轮的基节误差来确定,文献[2]给出了齿轮最大修形量的表达式:
Emax=Δ+δmax。
其中:δmax为啮合齿对最大综合变形量;Δ 为啮合齿对在啮入或啮出位置可能存在的最大干涉量。
2.2 修形高度的确定
修形高度一般表示修形曲线在齿廓上的修形位置。齿廓修形中,主要对双齿啮合区进行修形,在双齿啮合区进行修形能够避免齿轮在单齿啮合区过渡到双齿啮合区发生的啮合干涉现象[3]。
依据啮合原理,计算齿轮修形位置啮合线的长度。在啮合齿对中,小齿轮修形位置啮合线的长度为:
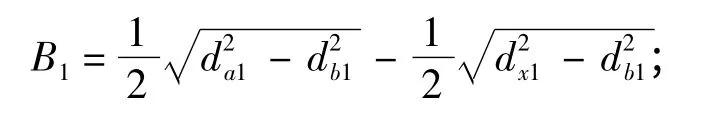
大齿轮修形位置的啮合线的长度为:
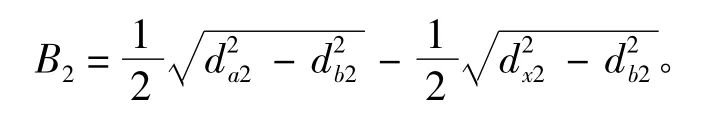
式中:da1和da2为小齿轮和大齿轮的齿顶圆直径;db1和db2为小齿轮和大齿轮的基圆直径;dx1和dx2为小齿轮和大齿轮的修形起点x 处的直径;B1和B2为小齿轮和大齿轮对应的双齿啮合区啮合线的长度。
啮合齿轮修形起点x 位置的起始圆直径为:
小齿轮
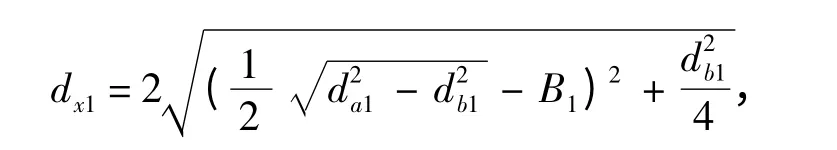
大齿轮
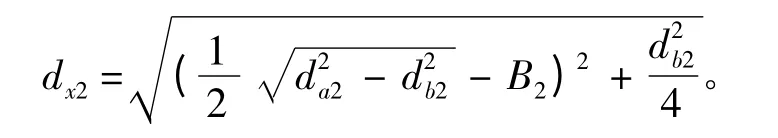
齿廓修形中,修形部分的啮合线长度为[4]:
B=Pb(ε-1)。
式中:Pb为齿轮基节;ε 为齿轮端面重合度。
2.3 修形曲线的确定
齿廓修形曲线主要有线性和二次曲线。应用分析说明二次曲线修形相对于线性修形来说,在改善传动系统动态性方面拥有更佳的优越性,因此本文采用二次曲线对轮齿进行齿顶修形。
二次曲线修形是沿着齿廓滚动角进行的,齿廓上的修形量与渐开线滚动角具有一定的关系。图1是齿顶修形的原理图,线性与二次修形曲线方程可以表示为:
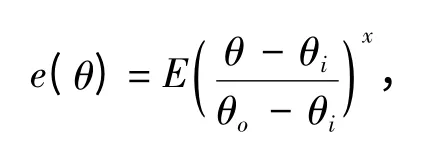
式中:e(θ)为随滚动角θ 变化的材料去除量;E 为修形量;θi和θo分别为修形起始点和齿顶处的渐开线滚动角。
当式中的x=1 时为线性修形,当x=2 时为二次曲线修形。
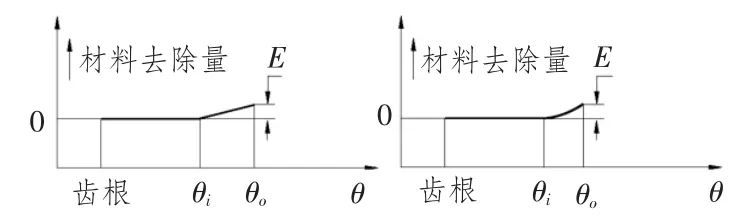
图1 齿廓修形原理图Fig.1 Profile modification schematic diagram
3 齿向修形参数
齿向修形方式一般包括齿端倒坡和齿向修鼓。文中齿向修形采用齿向修鼓的形式。
3.1 修形量确定
本文应用鼓形修形的方法对齿轮进行齿向修形,修形原理如图2所示。在图中ζ 为齿宽方向位置参数,ε 为鼓形修形量。
文献[5]同时考虑原始啮合齿向误差和接触变形,给出了鼓形量的计算公式:
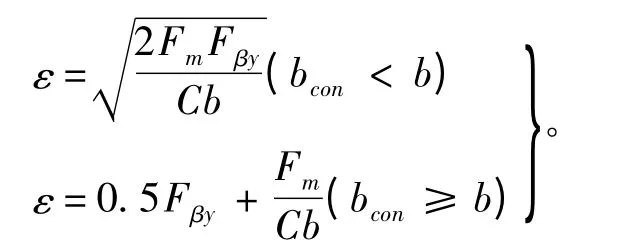
式中:Fm为圆周力;Fβy为啮合齿向误差;C 为啮合综合刚度;b 为齿宽;bcon为接触宽度。
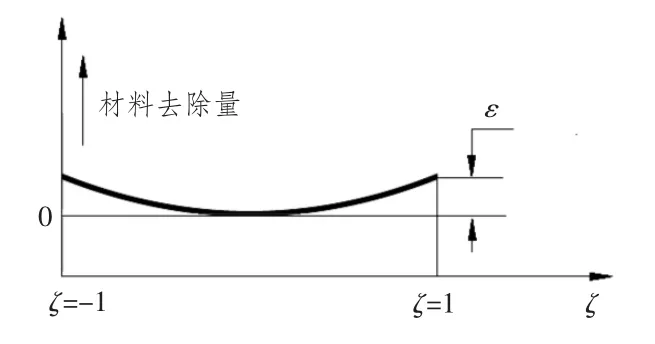
图2 齿向修形原理图Fig.2 Axial Modification schematic diagram
4 齿面修形对行星传动系统动态特性的影响
4.1 有限元模型
行星齿轮传动系统在有限元软件中进行建模,齿轮接触分析采用半解析方法对齿轮进行接触计算。利用该软件对行星齿轮传动系统进行齿轮修形前后的有限元接触分析,比较修形前后传动系统动态特性。行星齿轮传动系统结构如图3所示。
图3 行星齿轮传动系统结构图Fig.3 The structure diagram of planetary gear transmission system
在接触分析过程中,首先对未修形的轮齿进行啮合接触分析,得到各个轮齿在啮合位置的最大变形量,求得齿廓修形量幅值E;根据行星齿轮传动系统的传动特点,对太阳轮和行星轮进行曲线齿廓修形以及齿向修鼓;对内齿圈不做修形处理。所用接触分析模型如图4所示。各齿轮参数见表1。

图4 行星齿轮传动系统有限元模型Fig.4 The finite element model of planetary gear transmission system
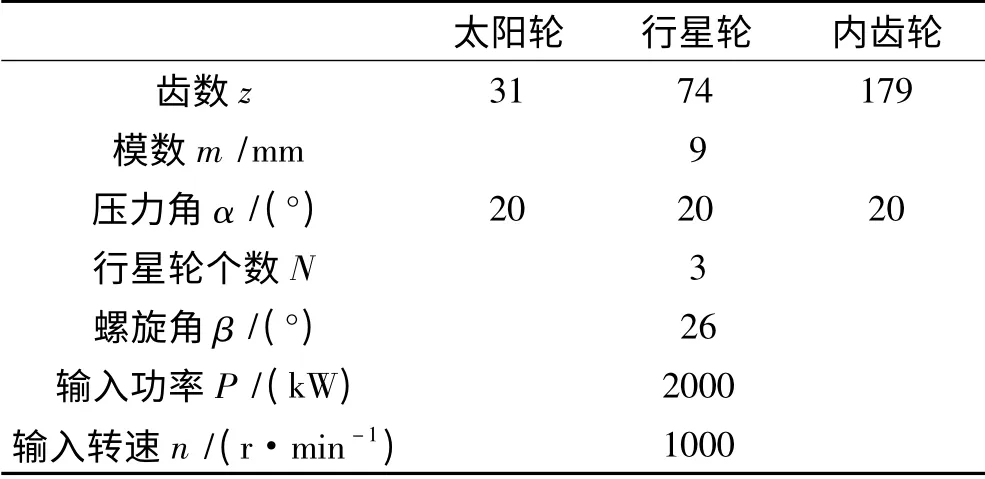
表1 行星齿轮传动系统参数Tab.1
根据文中修形参数确定方法,给出行星齿轮传动系统修形齿轮齿面修形曲线如图5和图6所示。

图5 太阳轮齿面修形曲线Fig.5 The gear modification curve of sun gear
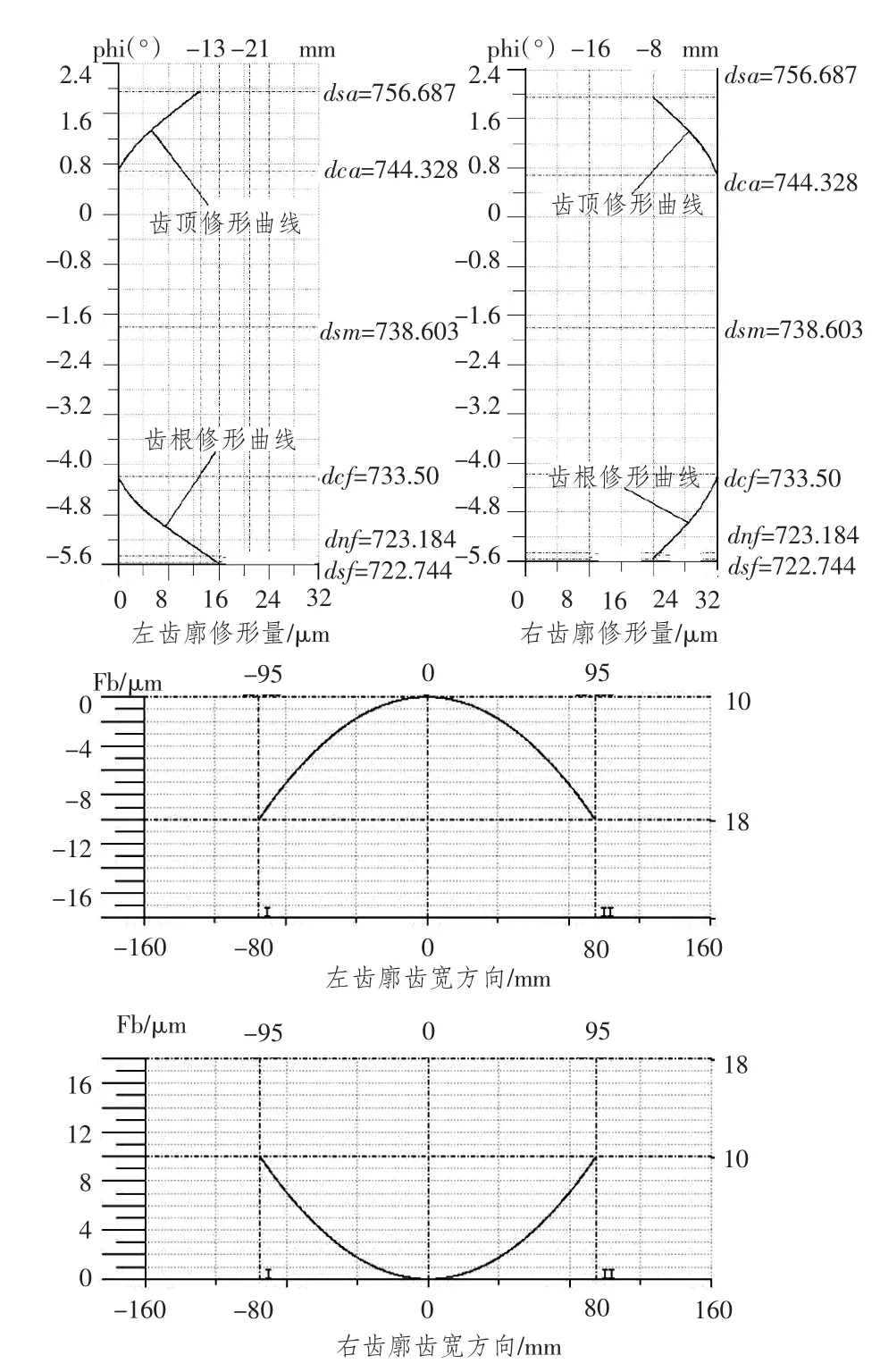
图6 行星轮齿面修形曲线Fig.6 The gear modification curve of pinion
4.2 齿面修形对行星齿轮传动系统动态特性的影响
本文重点通过啮合仿真分析研究齿轮修形对齿轮传动系统动态特性的影响。这里考虑修形对传动系统的内部激励以及轮齿之间动态啮合力的影响。内部激励主要包括刚度激励、误差激励和啮合冲击激励,内部激励是使齿轮传动系统产生振动噪声的最主要因素;轮齿间的动态啮合力的时变性对系统传动的平稳性具有重要的影响。限于篇幅,本文只针对太阳与行星轮进行分析,行星轮与内齿圈分析结果和太阳轮与行星轮分析结果一致。
1)修形对刚度激励的影响
图7 分别给出了轮齿修形前后,太阳轮与行星轮之间的啮合刚度曲线的对比情况。从图中的啮合刚度曲线可以得出,轮齿修形后,啮合刚度波动幅值减小,啮合刚度曲线振动幅值降低,这一结果反映到传动特性上,表现为啮合传动变得更加平稳,降低了系统的振动特性。
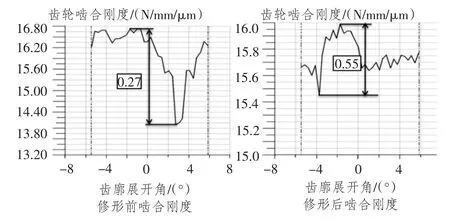
图7 太阳轮与行星轮啮合刚度Fig.7 Mesh stiffness between sun and pinion
2)修形对误差激励的影响
图8 中的传动误差曲线可以发现,修形前传动误差曲线总体波动比较明显,这说明齿轮在啮合过程中的基节偏差和齿形偏差很大,从轮齿修形后的传动误差曲线可以看出,传动误差曲线波动减小,说明轮齿修形能让齿轮系统工作更平稳。
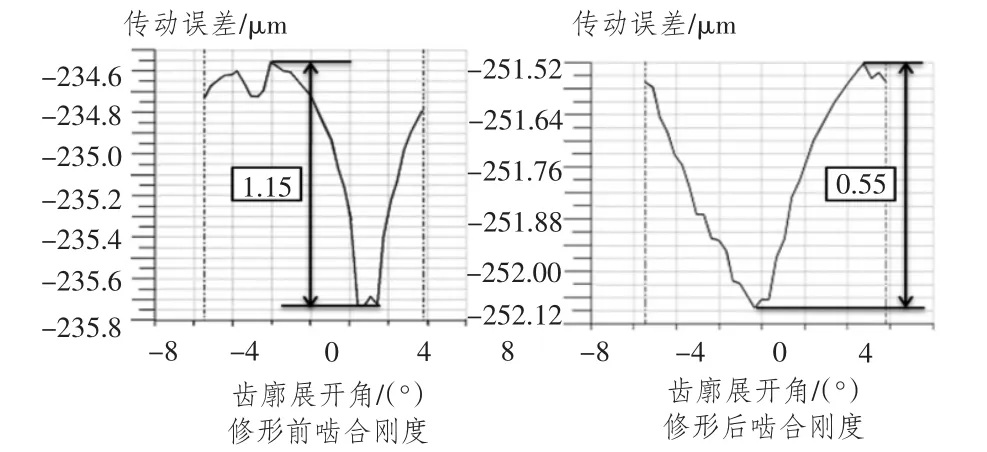
图8 太阳轮与行星轮传动误差曲线Fig.8 Transmission error between sun and pinion
3)修形对啮合冲击激励的影响
如图9所示,通过对比太阳轮与行星轮在修形前后的载荷分布可知,轮齿修形前,齿轮在啮入和啮出时刻存在载荷突变现象,这主要是因为轮齿啮入啮出时刻,存在啮入啮出冲击造成的,这是形成啮合冲击激励的主要原因,通过修形可以发现,轮齿在啮入啮出位置的载荷突变得到改善,避免了齿轮在工作过程中产生的动载荷。从而有助于降低传动系统的振动噪声问题。

图9 太阳轮与行星轮啮合载荷分布Fig.9 The load distribution between sun and pinion
4)修形对齿面啮合力的影响
图10 表示轮齿修形前后太阳轮与行星轮之间动态啮合力的变化情况。图中显示,齿轮传动在经历了初期的振动波动后,进入稳定啮合状态,动态啮合力则呈现为周期变化。轮齿修形前啮合力的波动幅值较大,修形后啮合力波动幅值明显降低,这在动力学特性上表现为传动载荷的平稳性,降低了系统的振动噪声,改善了齿轮传动系统的动态特性。
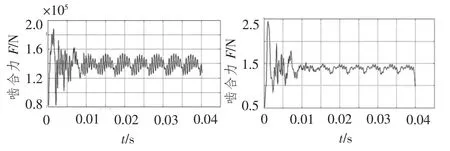
图10 太阳轮与行星轮间的动态啮合力Fig.10 The dynamic mesh force between sun and pinion
5 结 语
通过本文分析可以得到以下几点结论:修形能够改善传动系统刚度激励、误差激励和啮合冲击激励,从而降低系统的振动特性;修形能够改善系统在啮合过程中的动态啮合力,使得动态啮合力的波动幅值降低,增加传动系统传递载荷的平稳性,降低系统的振动噪声。
综上所述,通过轮齿的优化修形,能够从各个方面改善齿轮传动系统动态啮合特性,能够有效的降低传动系统的振动噪声问题,因此在齿轮传动系统中轮齿修形十分必要,同时也证明上文提到的齿轮优化修形方法对改善传动系统动态特性十分有效。
[1]齿轮手册—渐开线圆柱齿轮修形计算[M].北京:机械工业出版社,2000.
[2]孙月海,张策,葛楠.含误差的直齿轮的齿廓修形[J].机械工程学报,2003,39:12.
[3]刘国华,李亮玉.含间隙和时变啮合刚度的渐开线齿轮副齿廓修形研究[J].中国机械工程,2007.
[4]温建民.低振动噪声齿轮系统的非线性动力学特性及其修形研究[D].上海:同济大学,2007.
[5]宋乐民.齿形与齿轮强度[M].北京:国防工业出版社,1987.
