基于测波雷达现实方向谱的三维波浪数值模拟研究

王作超，石爱国，吴 明，刘 猛

(海军大连舰艇学院，辽宁 大连116018)

0 引 言

传统海浪环境的描述，一般是从频率和波浪能量关系的角度，采用海浪频谱来进行研究。这样的海浪频谱是假设海浪能量只沿一个方向传播，所以一般也被认作单方向海浪谱。

实际上，波浪沿多个方向传播。因此要更加准确地描述波浪环境，必须把波浪能量的方向分布情况描述出来，由此产生了方向谱的概念。海浪的方向谱描述了波浪能量随频率和方向的分布情况。显然，在海运工程、船舶设计、船舶性能计算等领域，与海浪频谱相比，方向谱可以生成更为接近真实的海洋环境，具有更大的优势。因此，自20世纪90年代起，有越来越多的学者从物理水池、数值水池(NWD)等方面开展了大量方向谱的研究工作［1］。近年来，随着计算机计算能力的大幅提高，基于方向谱的数值水池研究更是发展迅速［2－3］。目前，方向谱研究领域存在的一个普遍问题是将方向谱一般看作频谱和方向扩散函数乘积的统计谱［4］，同真实的海浪环境仍有差别，因此利用真实波浪的观测谱代替统计谱就成为深化数值波浪模拟研究中的必然课题。

在现有的各种方向谱观测手段中，诸如遥感、水面、水下测波仪器，虽然类型不少，也各有特点，但可装载于舰艇，且简便易行，能实时获取波浪信息，并具有较高观测精度，目前唯有X 波段雷达测波系统。

自20世纪60年代，Oudshoorn 等［5］开始探索利用雷达获取海浪信息以来，经过近50年的发展，这一技术已趋于成熟。其中，德国GKSS 研发的WaMoSⅡ［6］，通过了德国船级社(GL)与挪威船级社(DNV)的认证，并得到了广泛安装和应用，具有代表性。为此，本文将WaMoSⅡ所采集的真实海浪信息代替传统的统计谱用于三维波浪的数值模拟，其成果将提高数值水池造波的仿真度，有助于提高船舶耐波性的预报水平。

1 测波雷达

雷达测波的系统组成、测量流程可以参考文献［5，7－9］。测波雷达系统会受到障碍物、雨水、降雪等外界环境的影响，影响测量的准确性。为了数据的可靠性，WaMoSⅡ在系统中引入数据质量因子IQ(Quality Index)，以此判别所获信息的准确性，只有当IQ 为000 时，才表示所获数据可靠［10］。

本文所用的WaMoSⅡ测波设备，能测量海区波浪的频谱和方向谱，主要测量参数如表1所示。

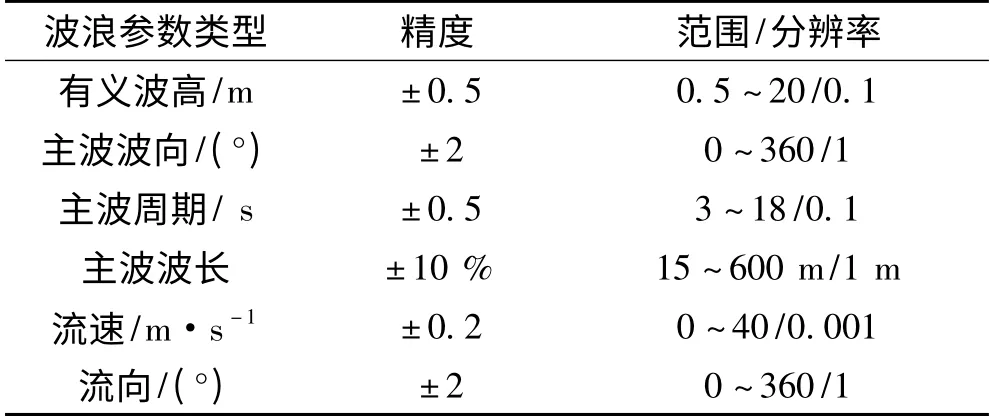
表1 WaMoSⅡ测量浪参数Tab.1 Measurement wave parameter of WaMoSⅡ

2 数值水池

短峰不规则波可视为无限多个频率不等、方向不同、振幅变化且相位随机的微幅简谐波叠加而成。在空间位置(x，y)处，t 时刻的波面高度可表示为:

式中:aij为第i 个频率、第j 个方向的成分波的波幅;ωi、ki分别为第i 个频率的成分波的圆频率和波数;θj为第j 个方向的成分波的方向;εij为第i 个频率、第j 个方向的成分波的随机相位角，是［0，2π］区间内均匀分布的随机数。

其速度场的表达式为:

方向谱密度可分解为:

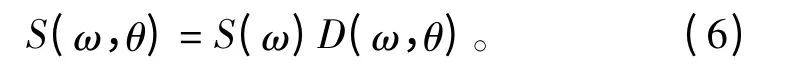
式中:S(ω)为频谱;D(ω，θ)为归一化的方向分布函数。一般的海浪研究和海浪数值模拟，S(ω)取统计谱，它通过长时间的观测得到，反映了海浪谱的一般规律，同真实海浪差别较大。图1 为WaMoSⅡ实测的频谱和以相同参数条件计算的ITTC 双参数谱对比图。从中可以看出二者的明显差别。就这一具体海区的海浪状况而言，实测谱的能量更高，也更为集中。

图1 WaMoSⅡ频谱和ITTC 谱频对比图Fig.1 The comparison of spectrum between WaMoSⅡand ITTC

据此，本文直接采用WaMoSⅡ的实测数据，从其所给的方向谱数据文件中提取方向、频率和对应的谱密度值，以求营造更真实的海浪环境。

本文数值模拟中的控制方程及其离散、湍流模型可参考文献［2］。采用边界造波法生成波浪［11］，采用阻尼消波法实现消波［12］。

3 数值计算

3.1 数据描述

根据上文提到的WaMoSⅡ有关数据的质量要求，本文选取了“海洋22”号于2009年9月13日1 000 时刻观测的方向谱信息。其有义波高为3.8 m，平均周期9.6 s，主波向67 °，IQ 为000。WamosⅡ提供的方向目标谱如图2所示。

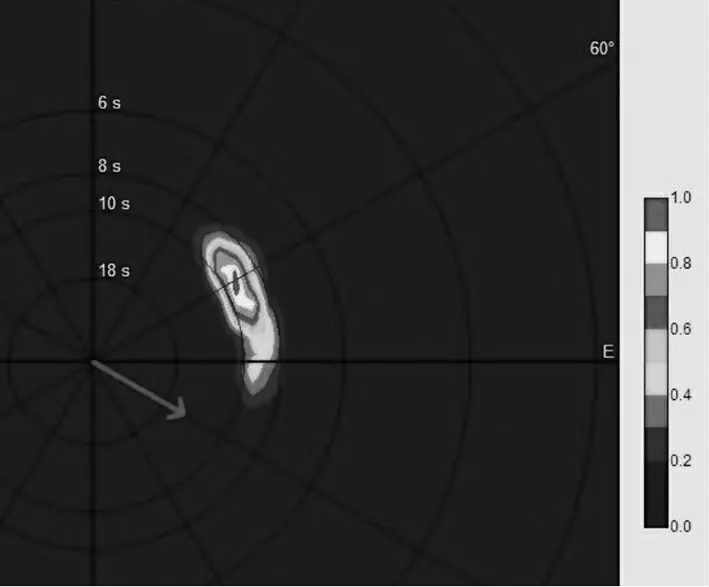
图2 WaMoSⅡ提供的方向谱(Date:20090913 Time:1000)Fig.2 The directional spectrum given by WaMoSⅡ(Date:20090913 Time:1000)

从图2 中可以看出，所选样本数据的能量主要集中在40 ° ～110 °之间，其他角度的能量可忽略不计。

3.2 求解绝对谱密度函数

当利用海浪谱进行数值波浪模拟时，其需要具有绝对谱密度值的方向谱。而WaMoSⅡ给出的是幅值归一化的相对方向谱，不能满足要求。本文利用谱形相似条件，将相对方向谱密度解算为绝对方向谱密度。求解过程如下:

1)采用辛普森法，求得相对方向谱的谱体积

2)根据测得的H1/3，由求得真实的海浪方差mt。

3)计算谱值比例系数:

4)求解绝对谱密度函数:

根据上述步骤，解得所采数据的mf=41.137 6，k=0.021 8，完成相对谱密度值向绝对谱密度值的转换。

3.3 计算设置

各项设置如表2所示。

表2 计算设置Tab.2 The setting up of numerical simulation

3.4 边界条件设置

1)造波区入口边界——速度入口，给定波浪沿3 个方向的分速度，根据波高给出水的体积分数及k，ε 值;

2)消波区入口边界——速度入口，给定流速沿3 个方向的分速度，根据静水面位置给出水的体积分数及k，ε 值;

3)上下边界——速度入口，给定3 个方向流速及水的体积分数;

4)出口边界——压力出口，设定静压力、底面位置和自由面高度，回流的湍动能k，耗散率ε。

图3 计算域及边界设置Fig.3 Grid domain and setting up of boundary layer

4 数值模拟结果及分析

4.1 频谱分析

在短峰不规则波的模拟中，采用虚拟5 点浪高仪阵列(见图4)监测波面时历。图5 中给出的是所模拟的短峰波瞬时波面图。图6 是5 点的部分波高时历。

根据所采集的波浪时历，经FFT 得到频谱，同时与WaMoSⅡ给出的目标频谱和同参数条件下求解的ITTC 谱进行比较(见图7)。由图中可以看出，相较于目标频谱，通过数值模拟所获的频谱能量虽有所衰减，但谱形吻合程度较高。为抑制衰减，可采取网格加密、改变网格分布及尺寸等措施。

图4 浪高仪阵列Fig.4 The probe array of surface elevation

图5 短峰波的瞬时波面图Fig.5 The animation of surface of short crested wave

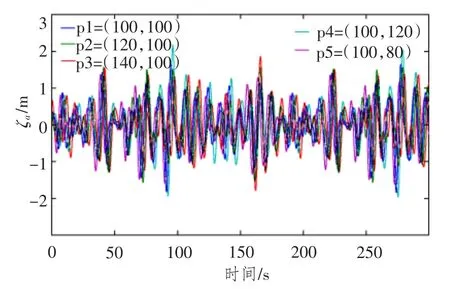
图6 浪高仪阵列波面时历Fig.6 The time history of surface elevation of probe array

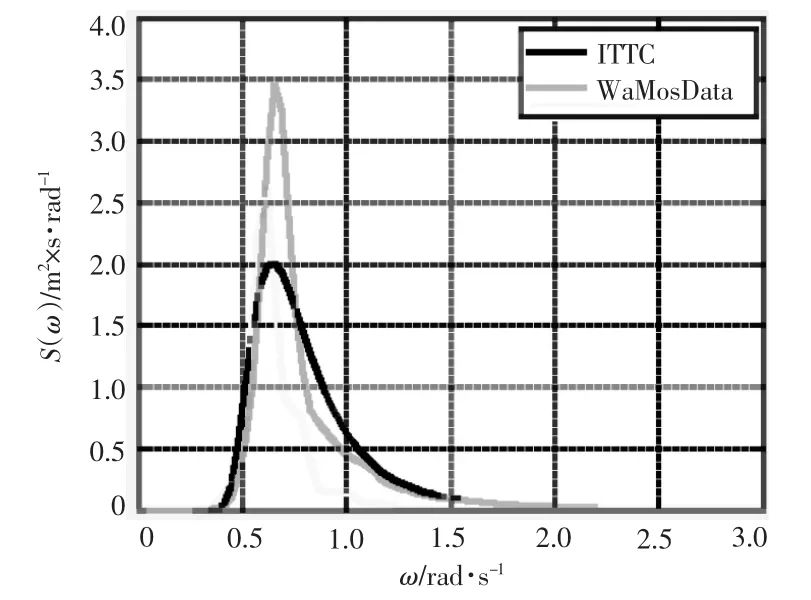
图7 频谱对比图Fig.7 The comparison of spectrum of NWD，ITTC and WaMosⅡdata

4.2 方向谱分析

方向谱主要的分析方法有:直接傅里叶变换方法(DFTM)、参数法(PM)、最大似然法(MLM)、扩展的最大似然法(EMLM)、最大熵法(MEP)和贝叶斯方法(BDM)［13－14］。上述方法中，BDM 法具有较高的分辨率，当阵列仪器数不少于4 时就能给出符合实际的方向分布，受仪器间距、方向分布宽度以及互谱误差影响最小［15］。故本文采用BDM 法对所获的波面时历进行方向谱分析，给出波能随方向的分布情况(见图8和图9)，获得的三一波高、平均周期、主浪向等参数如表3所示。

图8 数值模拟的三维波方向谱Fig.8 The 3－directional spectrum of numerical simulation

图9 数值模拟的方向谱等值线图Fig.9 The contour of directional spectrum of numerical simulation

表3 所获参数与目标值对比Tab.3 The comparison of parameters between numerical simulation and WaMosⅡ

从模拟结果看，与WaMoSⅡ的目标方向谱谱形吻合较好，除有义波高外，波浪的平均周期和主浪向与目标值均较为接近，模拟精度较高。考虑到计算效率和模拟精度，在造波过程中，对WaMoSⅡ给出的原始数据，删除了部分对谱密度值影响较低的角度和频率，这是导致方向谱、频谱波动的总能量同目标能量有一定偏差的原因之一。

5 结 语

本文基于WaMoSⅡ给出的方向谱数据开展的三维波浪数值模拟，达到了较高模拟精度，与传统的统计谱相比，能更好地模拟真实海浪，为后续船舶耐波性的研究提供了更加真实的海浪环境。

本文的三维波浪数值模拟，受限于现有的计算资源和计算能力，在权衡计算效率与计算精度后，在网格、频率、角度的选取上做了一定的舍取，对波浪模拟的准确性有一定影响。随着计算机硬件技术的发展与波浪模拟算法的改进，对真实海浪环境的数值模拟必将精度更高、耗费时间更短，更加实用化，用于海上作业实践。

需要指出的是:本文的意义，在于为在航船获取实时的真实海浪环境，实现风浪航行优化决策的创新作业模式，提供了技术支撑。

［1］ALLENDER J，et al．The WADIC Project:a comprehensive field evaluation of directional wave instrumentation［J］．Ocean Enginering，1989，16:505－536．

［2］吴乘胜，朱德祥，顾民．数值波浪水池及顶浪中船舶水动力计算［J］．船舶力学，2008，12(2):171－179．

WU Cheng-sheng，ZHU De-xiang，GU Min．Computation of hydrodynamic forces for a ship in regular heading waves by a viscous numerical wave tank［J］．Journal of Ship Mechanics，2008，12(2):171－179．

［3］冯光，吴乘胜，郑文涛，等．数值水池短峰不规则波模拟研究［J］．船舶力学，2010，14(4):347－354．

FENG Guang，WU Cheng-sheng，ZHENG Wen-tao，et al．Reproduction of short-crested irregular waves by a viscous numerical wave tank［J］．Journal of Ship Mechanics，2010，14(4):347－354．

［4］PARK J C，et al．Numerical reproduction of fully nonlinear multi－directional waves by a viscous 3D numerical wave tank［J］．Ocean Engineering，2004，31(11):1549－1565．

［5］OUDSHOORN H M．The use of radar in hydro-dynamic surveying［J］．Coastal Engineering，1960(7):59－76．

［6］Reference list［EB/OL］．http://www．oceanwaves．org /start．html．

［7］VALENZUELA G R．Theories for the interaction of electromagnetic and oceanic waves a review［J］．Boundary-Layer Meteorology，1978(19):87－105．

［8］YOUNG I R，ROSENTHAL W，ZIEMER F．A threedimensional analysis of marine radar images for the determination of ocean wave directionality and surface currents［J］．Journal of Geophysical Research，1985，90:1049－1059．

［9］ZIEMER F，GUNTHER H．A system to monitor ocean wave fields［C］．Proceedings of the Second International Conference on Air－Sea Interaction and Meteorology and Oceanography of the Coastal Zone，Lisbon，1994．

［10］WaMos Ⅱ Wave Monitoring System Operating Manual Installation Guide，2006，44．

［11］刘霞，谭国焕，王大国．基于边界造波法的二阶Stokes 波的数值生成［J］．辽宁工程技术大学学报(自然科学版)，2010，29(1):107－111．

LIU Xia，TAN Guo-huan，WANG Da-guo．Numerical simulation of second-order Stokes based on wave-generation method of defining inlet boundary conditions［J］．Journal of Liaoning Technical University(Natural Science)，2010，29(1):107－111．

［12］李凌，林兆伟，尤云祥，等．基于动量源方法的黏性流数值波浪水槽［J］．水动力学研究与进展(A 辑)，2007，22(1):76－82．

LI Ling，LIN Zhao-wei，YOU Yun-xiang，et al．The numerical wave flume of the viscous fluid based on the momentum source method［J］．Journal of Hydrodynamics(Ser．A)，2007，22(1):76－82．

［13］HASHIMOTO N，NAGAI T，ASAI T．Extension of maximum entropy principle method(MEP)for estimating directional wave spectrum，24thInt．Conf．Coastal Eng，1994，11:232－246．

［14］HASHIMOTO N，KDBUNE K，KAMBYAMA Y．Estimation of directional spectrum using the Bayesian approach，and its application to field data analysis［R］．Report of the Port and Harbor Research Institute，1987(26):57－100．

［15］柳淑学，俞聿修．方向谱的分析方法［J］．港口工程，1994(1):25－32．

LIU Shu-xue，YU Yu-xiu．The analytical methods of directional spectrum．Port Engineering［J］．1994(1):25－32．