基于α稳定分布模型的水声信号白化滤波方法

李宗吉，张西勇

(海军工程大学 新兵器技术与应用研究所，湖北 武汉430033)

0 引 言

在传统的水声信号检测理论中，干扰背景多被假设为高斯分布。但在实际应用中，尤其是主动声呐条件下，由于海洋噪声背景和混响的联合作用，干扰背景明显偏离了高斯分布，具有显著尖峰脉冲特性，其概率密度函数的衰减过程比高斯分布要慢，即呈现代数拖尾。

广义中心极限定理指出，无限个无限方差的独立分布同随机变量的极限分布是一种稳定分布，而α 稳定分布是唯一的满足广义中心极限定理的分布族，比高斯分布有更广泛的适用性。α 稳定分布的统计特性由其特征函数的4 个参数决定，其中最重要的参数为特征指数α ∈(0，2］，它决定着α 稳定分布概率密度函数拖尾的厚度。α 的取值越小，概率密度函数拖尾越厚，表明随机信号的尖峰脉冲特性越明显。因此，α 稳定分布可以很好地对水声干扰背景噪声信号进行描述。此外，α 能够在(0，2］之间任意取值，因此α 稳定分布可以更加灵活地对水声干扰背景噪声信号进行描述。特别地，当α=2 时，α 稳定分布与高斯分布完全相同，即高斯分布是α 稳定分布的特例。α 稳定分布都可以由SαS 分布变换得到，不失一般性，本文将主要讨论基于SαS 分布噪声建模的白化滤波方法。

SαS 分布没有显性的概率密度函数表达式，但其特征函数可由式(1)明确表达:

1 共变谱与稳定白噪声

对于SαS 分布过程，由于不存在二阶矩，其功率谱不存在。为了进行频域处理，引入共变谱的概念。

对于一个严平稳复SαS 过程{x(t);－∞＜t＜∞}，总存在如下一种谱表示:

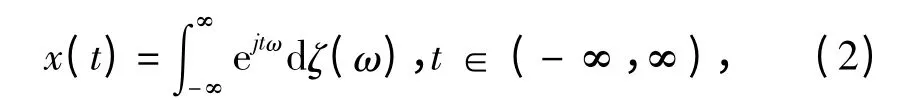
其中ζ(ω)的独立增量满足如下关系:

式中:C(p，α)为依赖于p 与α 的常量;Φ(ω)为x(t)的一种称作谱密度的非负函数。当α=2 时，谱密度Φ(ω)就是对应高斯过程的功率谱;0 ＜α ＜2 时，谱密度Φ(ω)并不表示x(t)的功率谱。但在一些如线性预测与滤波的应用中，它起着和功率谱一样类似的作用，也就是说，谱密度Φ(ω)完全可以描述x(t)的一种频率分布。当且仅当dζ(ω)具有全向或者旋转不变增量时，过程{x(t)}为严平稳过程，并且有如下稳定过程的共变函数的表达式:

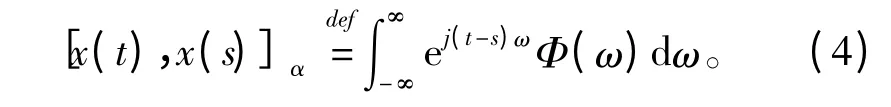
因此，稳定分布过程的自共变函数与二阶过程的自协方差函数有着同样的意义，它与谱密度Φ(ω)构成一个傅里叶变换对。根据自共变函数的定义:

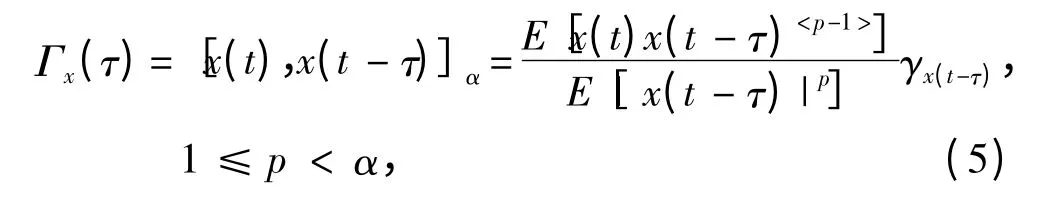
可以建立如下准则:当且仅当自共变函数Γx(τ)在理论上满足Γx(τ)=γxδ(τ)时，{x(t)}为稳定分布白噪声过程，其中δ(τ)是冲激函数。自共变函数是对二阶过程的自相关函数的广义化，对自共变函数Γx(τ)进行傅里叶变换可以得到一种分数阶谱——共变谱(Covariation Spectrum，CS):

若将自共变函数换成自相关函数，则得到功率谱密度函数。由于自相关函数是自共变函数当α=2时的特例，因此，二阶过程的功率谱是共变谱的特例，共变谱是功率谱的广义化形式。在离散时域，一个严平稳复SαS 序列{x(t)}也总存在如下一种谱表示:

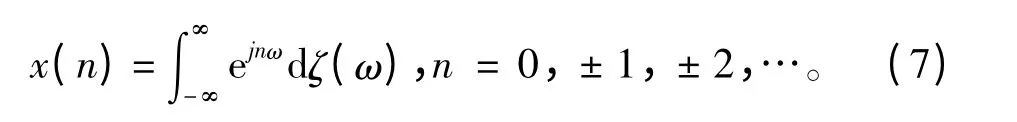
因此，一个稳定分布白噪声序列{x(n)}的自共变序列Γx(n)=［x(m)，x(m－n)］α应为序列γxδ(n)，其共变谱理论上应是平坦均匀直线。

2 基于广义Yule-Walker 方程的白化滤波

对SαSAR(P)序列x(n)作如下改写:

其中u(n)是一个特征指数为α，分散系数为γ 的SαS 分布白噪声序列。

x(n)可以看成是无穷多个独立同分布稳定白噪声变量的线性组合，x(n)与u(n)具有相同的特征指数α。

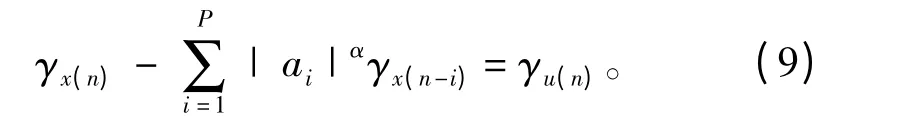
对于严平稳稳定分布序列x(n)，其离差应该满足:

可以得到x(n)的离差如下式所示:

因此，严平稳稳定分布序列x(n)是与u(n)具有相同的特征指数α、分散系数为γx(n)的稳定有色噪声。

当满足条件1 ＜α ≤2 时，在差分方程式(8)的两端分别取关于x(n－m)的共变函数，可以得到:

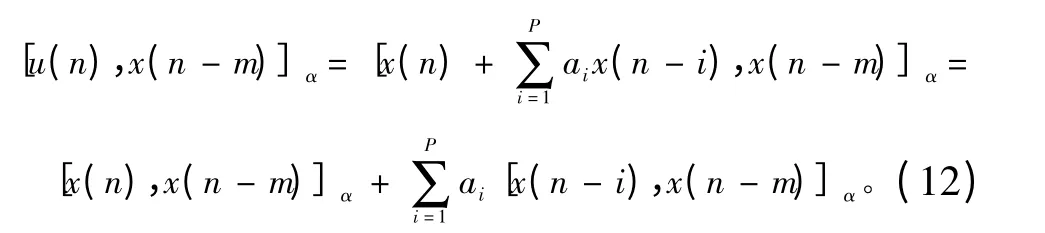
可以得到:

即

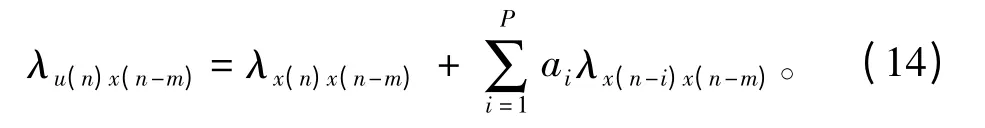
式中:λu(n)x(n－m)为u(n)和x(n－m)的共变系数，记为λux(m);λx(n)x(n－m)为x(n)的自共变系数，记为λ(m)。

共变系数λux(m)和滤波器的脉冲响应相关，可得

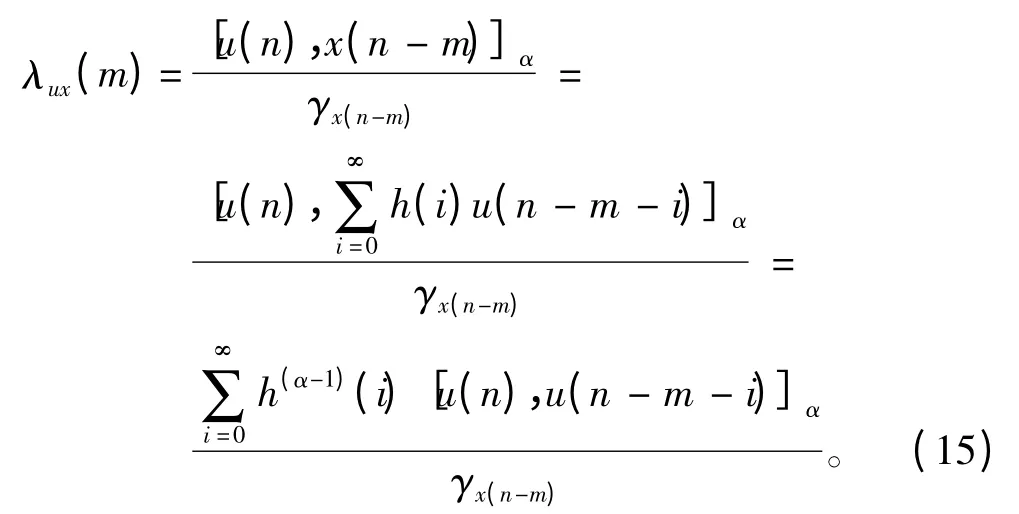
上式最后一步利用了共变的伪线性。u(n)是稳定白噪声，满足如下条件:

结合式(12)、式(14)～式(16)可得:

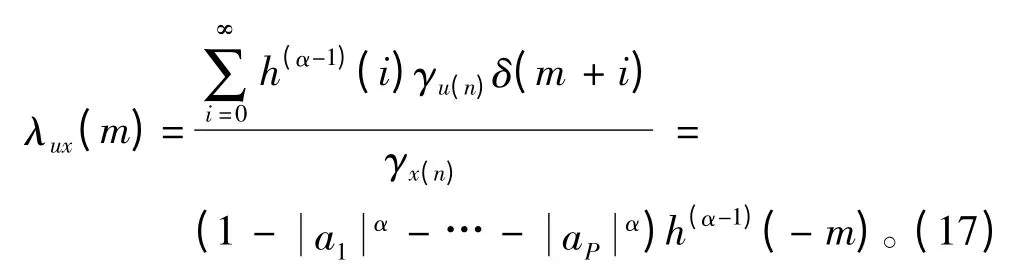
因此，对于一个SαSAR(P)过程，自共变系数存在如下关系:

SαSAR(P)参数矢量a 可以通过求解Yule-Walker 方程组得到。

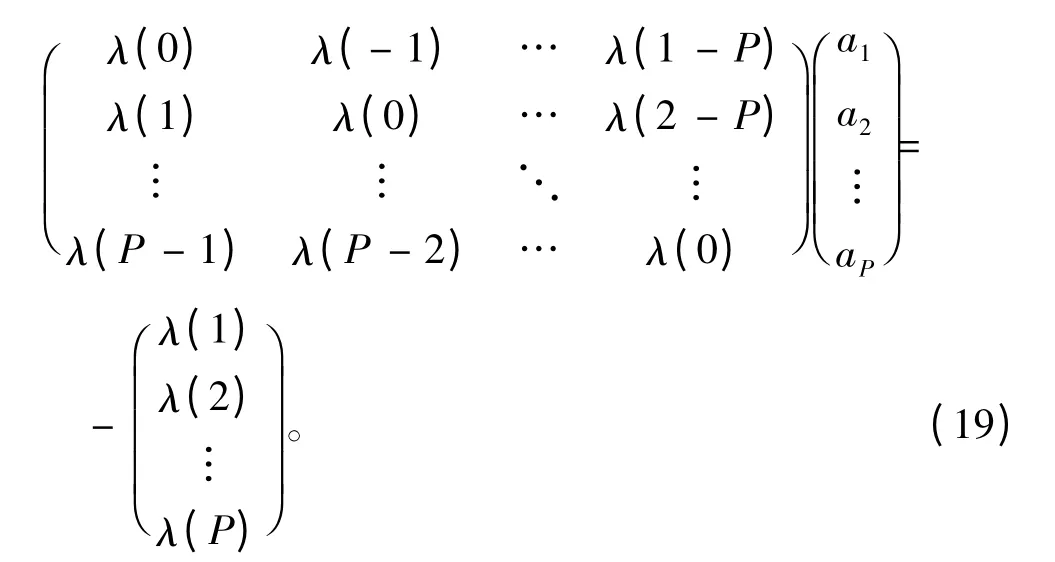
将使用自共变系数描述的Yule-Walker 方程称为广义(或分数低阶)Yule-Walker 方程，记为Ca=p。稳定白噪声离差γu(n)的估计值^γu(n)可以用下面的等式计算得到:

对于高斯过程而言，自共变系数矩阵C 是对称和正定的。但对于非高斯过程而言，C 通常是非对称，甚至是奇异的。

3 自共变系数的估计

基于广义Yule-Walker 方程频谱估计算法的性能除了取决于算法本身，自共变系数λ(i)的估计也至关重要。在实际应用中，需要根据观测样本值估计自共变系数矩阵C和加权矢量p，即需要估计自共变系数λ(i)［2］。

对于任何1 ≤p ＜α，联合α 稳定分布随机变量X和Y 的共变系数可定义如下:

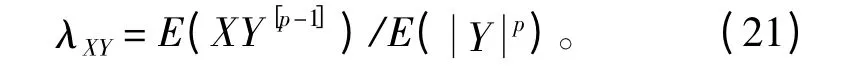
对于独立观测值(X1，Y1)，…，(XN，YN)，共变系数的估计值如下式所示:

为了简化计算量，可以令p=1，于是得到:

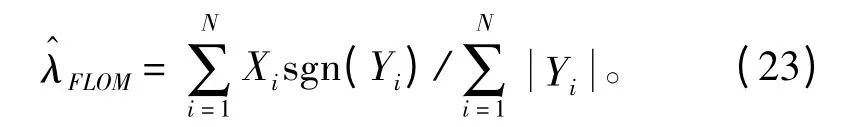
如果观测值独立，则上式一致收敛。然而，对于AR 过程，其输出序列并不满足独立性，但FLOM估计依然满足一致收敛［1］。在实际应用中，对于FLOM 估计，只需将式(22)和式(23)分别作如下改写:

4 预白化滤波及实验数据检验

在实际的主动信号检测中，往往采用滑动窗技术，对每次的窗内数据进行“谱估计→预白化→检测处理”。预白化滤波器的构建基于谱估计，得到AR 参数估计后，即可基于该估计建立起预白化滤波器。

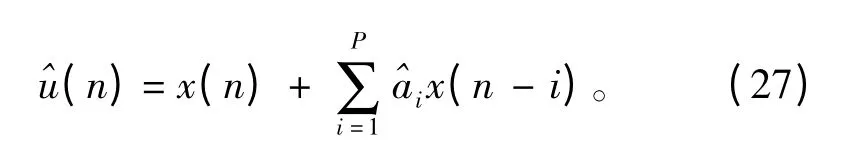
显然，这是具有MA 结构的滤波器。它可以从观测样本序列{xn}估计出激励序列{un}，式(27)亦被称为激励估计器。一般来说，AR 滤波有时亦被看作基于前P 个的观测样点预测当前样点的线性预测器，这样{un}亦是预测误差，该式又被称为线性预测误差估计器。

使用［0601 三亚海试］中一段基元级混响数据，发射信号为800 ～1 000 Hz 的HFM 脉冲，脉宽为4 s，采样频率为6 kHz。带通滤波已向发射通带两端各扩展50 Hz，即为750 ～1 050 Hz。数据长度与脉宽同长。使用广义Yule-Walker 方程算法对其进行AR(256)谱估计和预白化处理，设定p=1，处理结果如图1所示。由图1(b)可以看到，在全带内，观测样本拟合CS 曲线与观测样本统计CS 曲线重合得很好，经过预白滤波后，通带内成功实现了白化。

图1 一段海试数据预白化前后的CSFig.1 Covariation spectrum of a segment of sea trial data before and after prewhitened

需要指出的是，对于AR 模型阶数P 的选择目前尚无有效的定阶方法，因此在实际应用中，一般是凭借经验来指定AR 模型的阶数。在数据有效长度损失和运算时长允许的范围内，为了达到理想的预白效果，通常将阶数指定的偏高一些。

5 结 语

本文主要研究基于分数低阶统计量AR 模型参数的估计方法。首先，介绍共变谱、α 谱的概念以及稳定白噪声的判别准则，并采用实际海试数据检验分析了共变谱的性能;讨论一种基于α 谱的频域广义白化滤波方法。然后，从α 谱的角度出发，推导出基于自共变系数的广义Yule-Walker 方程。通过仿真深入讨论了基于广义Yule-Walker 方程频谱估计算法中，各参数对算法性能的影响。

本文第2 个主要研究内容是基于谱估计的预白化技术。对于AR 模型拟合的有色数据而言，预白实际上就是一个基于各AR 参数估计建立起来的MA滤波，亦即AR 激励估计，只要模型参数估计足够准确，就能得到理想的预白效果。采用大量水池实验、湖试、海试实际数据，考察了分数低阶白化滤波器的性能。

［1］SHAO M，NIKIAS C L.Signal processing with fractional lower order moments:stable processes and their applications［J］.Proceedings of the IEEE，1993，81(7):986-1010.

［2］查代奉.基于稳定分布白噪声的信号处理新方法研究［D］.大连:大连理工大学，2006:56-67.

ZHA Dai-feng.Study on new methods of signal processing based on stable white nolse［D］.Dalian:Dalian University of Technology，2006:56-67.

［3］WANG Z，HE Z，CHEN J.Robust time delay estimation of bioelectric signals using least absolute deviation neural Network［J］.IEEE Transacions on Biomedical Engineering，2005，52(3):454-462.

［4］MAKAR A.Estimation of the time delay of hydroacoustic signals for passive location of underwater objects［J］.Archives of Acoustics，2004，29(3):435-445.

［5］SO C.Analysis of an adaptive algorithm for unbiased multipath time delay estimation［J］.IEEE Transactions on Aerospace and Electronic Systems，2003，39(3):776-780.