织物热传递的数值模拟研究进展

张鹤誉，赵晓明，2，郑振荣，2

（1.天津工业大学，天津300387；2.天津工业大学教育部先进纺织复合材料重点实验室，天津300387）

近年来，计算机模拟仿真技术随着计算机硬软件技术的进步迅速发展，应用领域不断扩展。模拟仿真技术是指遵循相似原理（几何、环境及性能相似），用模型（物理模型或数学模型）代替实际系统进行试验和研究［1］。计算机数值模拟试验可得到大量复杂数据，更全面研究物理现象，也可评估大型实验装置，优化实验条件或实验参数，避免经济损失和人力浪费。在许多行业，如化工、冶金、建筑、航空航天、消防等，常要求所使用的纺织材料具有良好的隔热、阻燃特性，其性能测试大多在高温条件下进行，但实验条件难以控制，同时增加了研发成本和周期，浪费了资源。

从20世纪80年代后期开始，纺织材料的研究者们不断研发和改进织物热传递性能的数学模型［2］，模拟实验效果。这些实验模型从一维平面传热机制不断向二维、三维织物结构模型方向发展，模拟效果更加趋向于真实化。

1 织物模型的建立方法

数学模型的建立是对织物进行热传递性能数值模拟研究的基础，其建模方法主要有：几何方法、物理方法和混合方法［3］。早期研究主要基于织物几何特性建立模型，这种方法优点是模拟速度快，但它未考虑织物的物理属性。基于物理特性的建模方法是近年来织物建模的发展重点，尽管计算复杂，但它具有三维构型和动态模拟，效果真实。混合建模方法是几何方法和物理方法的结合，在纺织领域，目前仅处于研究的初级阶段。

2 热传递的基本理论

织物热传递的基本方式有热传导、热对流和热辐射三种［4］。

2.1 热传导

热传导是指完全接触的两个物体之间或一个物体的不同部分之间由于温度梯度而引起的内能交换。热传导遵循傅里叶定律：

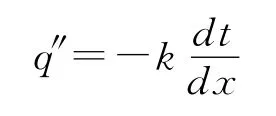
式中，q″为热流密度（W／m2）；k为导热系数（W／m－℃）；负号表示热量流向温度降低的方向。

2.2 热对流

热对流是指固体的表面与其他周围接触的流体之间，由于温差的存在引起的热量的交换。热对流分为两种：自然对流和强制对流。热对流用牛顿冷却方程来表示：

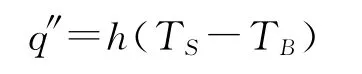
式中，h为对流换热系数；TS为固体表面的温度；TB为周围流体的温度。

2.3 热辐射

热辐射是指物体发射电磁能，并被其他物体吸收转变为热的热量交换过程。在工程中通常考虑两个或两个以上物体之间的辐射，系统中每个物体同时辐射并吸收热量。它们之间的净热量传递可以用Stefan－Boltzmann（斯蒂芬－波尔兹曼）方程来计算：

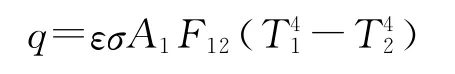
式中，q为热流率；ε为辐射率（黑度）；σ为Stefan－Boltzmann常数，约为5.67×10－8W／（m2·K4）；A1为辐射面1的面积；F12为辐射面1到辐射面2的形状系数；T1为辐射面1的绝对温度；T2为辐射面2的绝对温度。由上式可知，包含热辐射的热分析是高度非线性的。

3 织物热传递数值模拟的研究进展

利用数值模拟方法对纤维多孔材料的热传递性能进行模拟，可为各种纤维隔热产品的设计、隔热性能的评估和优化等提供重要的理论基础。近年来，国内外的一些研究团队在利用数值方法对纤维隔热材料的隔热性能进行评估方面做了一些有益的尝试。

采用有限体积法建立数学模型，最初是将织物单元看作简单三角形模型，进行稳态热分析，不能直观地表征织物的热传递性能。在此基础上，东华大学的巩彦如等［5］建立了简化的一维织物传热模型，将织物看作平面四边形单元，并在ANSYS软件中进行瞬态热分析，对不同热流密度下热防护材料的隔热性能进行了数值模拟，其模拟结果与试验测试结果相对误差在5%以内。范金土等［6－7］建立了热湿传递模型（见图1），将织物看成是匀质平板，该模型考虑了温度和水分含量对织物热传递的影响，模型中包括热传导和热辐射两种能量传递方式。通过对热湿传递的数值模拟，发现初始水含量、纤维层厚度和环境温度是影响热通量的三个最重要因素，此模型可以应用于功能织物的设计。V.P.Chandra Mohan等［8］研究了潮湿织物在对流干燥情况下，通过建立三维数值模型预测织物的瞬态温度和水分分布。该模型包括外部流场和温度场的建模以及内部温度场和湿度场的建模，全隐式格式的有限体积法用于控制瞬态热湿传递方程的离散化，同时假设计算流体动力学和热湿传递模型的耦合是一个方式。数值模拟结果表明该传热传质模型可以较准确地预测潮湿对象在不同温度和空气流速条件下，温度和水分含量的分布情况。

图1 热湿传递模型［6］

采用有限差分法和有限元法模拟织物热传递模型，朱方龙等［9］建立了火灾环境下的一维径向传热模型，如图2所示，假定人体为圆柱体，依据实际情况在模型的织物和皮肤之间设置微小空气层，形成了“织物－空气层－皮肤”物理模型，通过有限差分法对模型进行数值模拟计算，织物表面的温度模拟结果与实验结果相当吻合。该模型可用于个体防护装备的热设计，但未考虑含湿量对热传递性能的影响。中山大学的罗笑南等［10－11］建立了一种二维织物热湿传递的数值模型，通过对模型的分离、有限差分分析、定义边界条件然后进行数值分析，结果预测的温度和水汽分布与实验数据吻合良好，该模型未考虑辐射与对流影响，可模拟织物的瞬态热湿传递。浙江理工大学的徐定华等［12－13］研究了低温条件下双层纺织材料的建模、数值模拟及算法，基于稳态热湿传热模型，通过有限元算法用于非线性常微分方程和一维最小化问题的直接搜索方法，构建了正则化解的迭代算法。分析在不同环境条件下的数值模拟结果，得到了Hooke－Jevees的直接搜索方法，此方法可以有效地解决双层纺织材料的类型设计反演问题，同时数值模拟试验验证了该算法的有效性和逆问题提法的合理性。

图2 “织物－空气层－皮肤”系统圆筒形模型［9］

目前研究的织物传热模型大都是建立在二维直角坐标系下，将织物单元简化为匀质平板或圆柱体，这样可以降低建模难度，但也丧失了织物真实的组织结构，影响到数值模拟的精确度。加州大学的潘宁等［14］研究了纤维材料的相关参数对有效热导率的影响，模拟结果表明织物的聚集结构对纤维材料的热传递性能有很大影响。朱方龙［15］初步研究了织物组织结构对热传递的影响，针对火灾等高温环境下采用有限差分法对热防护织物的有效导热系数进行数值模拟。上述研究表明织物的几何形态结构很大程度上会影响到热量在组织内部的传递性能，所以建立织物三维组织结构的热传递模型是今后研究的重点。织物三维立体模型的建立是对织物进行热传递数值模拟的的基础，因此模型愈趋向于织物真实组织结构，模拟结果的准确性愈高。

4 皮肤传热模型

热防护织物主要是用来降低热量在织物上的传递速率，对热防护织物或热防护服的防护性能评价，需要同时考虑热量在人体皮肤上的积聚和传递。皮肤传热模型的建立可以模拟热量在人体皮肤上的传递，人体皮肤传热一般用Pennes′模型进行模拟。其传热方程［16］为

式中：ρs为皮肤的密度，kg／m3；cps为皮肤的比热容，J／（kg·℃）；ks为皮肤的导热系数，W／（m·℃）；ρb为血液的密度，kg／m3；cp，b为血液的比热容，J／（kg·℃）；wb为血流灌注率，其值为0.001 25m3／（s·m3）。

宋国文［17］等研究了皮肤模型的变化对服装热防护性能的影响，研究表明，不同的皮肤模型和皮肤初始温度的分布可以极大地影响热量在假人服装上的传递。因此，选择一个精确的皮肤模型并将其标准化将有利于模型试验在热防护中的效果评价。

5 总结与展望

建立织物热传递的数学模型是现阶段研究的热点，从国内外对织物热传递的数值模拟的研究状况来看，织物传热模型一般建立在二维坐标系中，不能真实反映出织物几何组织结构，模拟结果与实际织物热传递过程有偏差。因此，织物热传递的数值模拟应向三维立体结构模型发展，根据不同的织物特性和研究目的，建立精确的织物数学模型，采用合适的求解方法对模型进行数值计算，对比数值模拟结果与实验结果，不断提高和改进织物的三维立体模型。织物热传递的数值模拟技术是一个有着广阔应用前景的技术，其发展将对新型隔热防护材料的设计、性能测试以及节约成本和资源，提高试验安全性等方面具有重要的实际意义和实用价值。

［1］刘宁，高成英等.柔性织物三维动态模拟中的网格剖分研究［J］.中山大学学报（自然科学版），2002，41（5）：105—107.

［2］万志琴.织物热防护中的吸热特性研究［J］.纺织学报，2004，25（2）：43—45.

［3］陈辉，沈毅.关于织物仿真技术的综述［J］.丝绸，2005（8）：42—45.

［4］胡海霞，孟家光.织物热传导机理的分析与探讨［J］.北京纺织，2005，6（26）：28—31.

［5］巩彦如，张璇等.热防护纺织材料隔热性能的数值模拟［J］.东华大学学报，2010，36（2）：115—117.

［6］Jintu Fan，Zhongxuan Luo，Yi Li.Heat and moisture transfer with sorption and condensation in porous clothing assembilies and numerical simulation［J］.International Journal of Heat and Mass Transfer，2000（43）：2898—3000.

［7］Jintu Fan，Wen Xinghuo.Modeling heat and moisture transfer through fibrous insulation with phase change and mobile condensates［J］.International Journal of Heat and Mass Transfer，2002，（45）：4045—4055.

［8］V.P.Chandra Mohan，Prabal Talukdar.Three dimensional numerical modeling of simultaneous heat and moisture transfer in a moist object subjected to convective drying［J］.International Journal of Heat and Mass Transfer，2010，（53）：4638—4650.

［9］朱方龙.火灾环境下应急救援防护服传热数值模拟［J］.纺织学报，2009，4（30）：106—110.

［10］Xiaonan Luo，Qingzhen Xu.A new numerical implementa－tion on 2Dheat and moisture transfer through fabric［J］.Applied Mathematics and Computation，2006，（174）：1135—1150.

［11］Qingzhen Xu，Xiaonan Luo.Numerical solution of a twodimensional simulation on heat and mass transfer through cloth［J］.Applied Mathematics and Computation，2005，（171）：843—852.

［12］Dinghua Xu，Yuanbo Chen，Xiaohong Zhou.Type design for bilayer textile materials under low temperature：Modeling，numerical algorithm and simulation［J］.International Journal of Heat and Mass Transfer，3013，（60）：582—590.

［13］徐定华，陈远波，程建新.低温环境下纺织材料类型设计反问题［J］.纺织学报，2011，9（32）：24—28.

［14］Moran Wang，Ning Pan，et al.Lattice Boltzmann modeling of the effective thermal conductivity for fibrous materials［J］.International Journal of Thermal Sciences，2007，（46）：848—855.

［15］朱方龙.基于辐射衰减特征的隔热防护织物有效导热系数简化模型［J］.纺织学报，2011，32（10）：57—60.

［16］朱方龙，张渭源.基于人体皮肤热模型的热防护服评价方法研究［J］.中国安全科学学报，2007，11（17）：134—140.

［17］Guowen Song，Roger Barker.Effects of Variations in Skin Model on Evaluation of Thermal Protective Clothing Performance［J］.Peer reviewed，2004，（11）：21—24.