直井－压裂井混合井网渗流理论研究

孟宝锋 （中石油大庆油田有限责任公司第八采油厂，黑龙江 大庆163514）

理论研究认为，在注采平衡的条件下，面积井网中的各种工作井主要引起储层中发生稳态或拟稳态渗流过程。无论是压裂开发还是压裂开采，其实质都是关系到如何优化普通直井与压裂直井混合布井方案，这就需要深入研究混合井网的渗流理论问题。

针对直井－压裂直井混合布井问题，研究思路是首先获得目标井网单元的压力场，通过对压力场微分获得井网单元的流体质点运动速度场，再通过迭代追踪方法获得井网单元的流场，进而能够在活塞式驱替条件下确定井网见水时间和驱替效率，为直井－压裂井混合布井方案优化提供理论基础。

1 直井－压裂井井网压力分布研究

1.1 单一普通直井排稳态压力分布

考察厚度为h、间距为2d的两平行断层均质地层系统，在断层中央有一口产量为q的生产井，坐标原点位于某一井点处，其镜像反演结果为间距为2a的平面无穷井列（见图1）。其稳态压力分布［1］为：

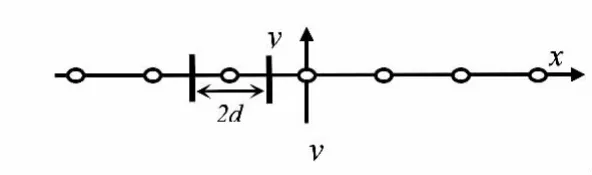
图1 单一普通直井排示意图

无量纲化为：

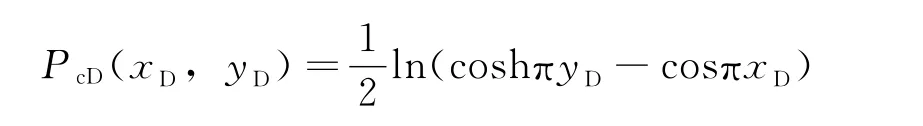
式中，h为地层厚度，m；2a为平行无穷井列间距，m；k为地层渗透率，mD；P为地层稳态压力，MPa；q为井的常流量，m3／d；μ为流体黏度，mPa·s；x，y为流体质点运动位置；xD，yD为无量纲流体质点运动位置。

1.2 单一压裂直井排稳态压力分布

在单一普通直井的研究基础上，通过使用叠加积分可以获得一排完全压开的垂直裂缝井的压力场。在如图2坐标系下，经过镜像反演，得到各裂缝井位置为［1］：

图2 单一压裂直井排示意图

则压力分布为：

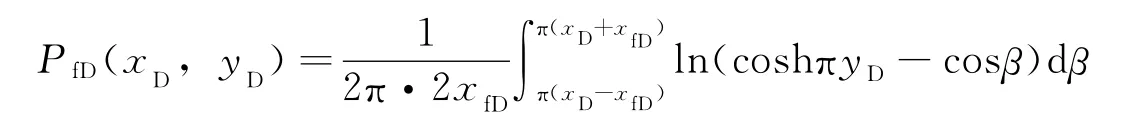
式中，n为压裂井数；β为流体质点任意位置与压裂井排夹角。

上述积分是比较难于获得显式结果的，但仍可通过对含有参变量的积分进行微分运算而得到流体质点平均速度场。

图3 直井－压裂对正井排示意图

1.3 直井－压裂直井对正井排压力分布

反九点井网是一种强注强采的井网，若将反九点井网单元中两侧的采油井改成注水井，则反九点井网将变成对正井排；若再对所有油井进行压裂，结果将形成如图3所示的井网形式。

根据多井压降叠加原理，这种井网所形成的无量纲稳态压力场可以表示为：

式中，b为排距，m；m为指标参数，取值－∞至＋∞。

上式的叠加表示是按井网单元写出的［2］，其计算容易得到较好的效果，坐标yD的变化恰好反映了多个井排叠加。对于油水两相渗流情况，需要假定液流流场是可以叠加的，即多井压降叠加理论也成立。

2 直井－压裂井流线追踪方法及分布特征

从注水井出发，注水井点无量纲坐标（0，0），注水伊始，水井压力分布不受任何干扰，相当于无限大地层中一口井的压力分布［3］：

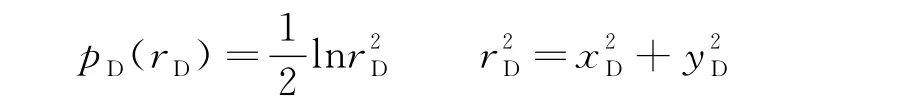
对于初始时间步，用θi表示第i个质点，其位置为：

对于下一个时间步，流体质点的位置为：

式中，θi为第i个质点运动角度；tD为无量纲流体质点运动时间；vD为无量纲流体质点运动速度。

压裂作业后，在压裂裂缝周围的形成线性流流线，使得井筒附近渗流阻力会变小。呈现其水驱前沿形状也有所改变，特别是在靠近压裂油井周围的部分，前缘变得平缓。

3 直井－压裂井网见水时间和水驱前缘运动规律

在流线追踪计算过程中，若记录在不同时刻各个流体质点所运动的距离（等时线），则可以得到水驱前缘运动形状（等饱和度线）［4］。

若已知流线（ψ），考虑在初始时刻注入井壁上（y＝0）一个小油珠（油质点）沿着最短流线以一定运动速度vψ运动，则运动距离Sψ为：

根据Darcy定律和Dupuit－Forchheimer关系式可知：

对于给定的流线，小油珠（油质点）运动的时间为：

对于直井 －压裂直井对井排问题，其最短流线是连接两井轴心的直线，即与y轴重合，由此得到最短流线上油质点的运动规律：

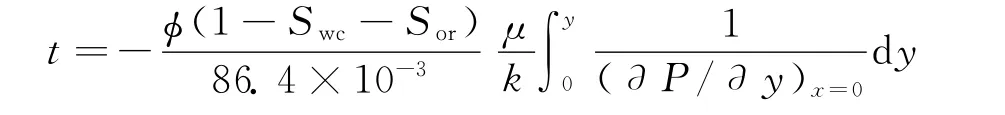
当积分上限等于井排距时（y＝b），得到注入水突破时间：

式中，tb为注入水突破时间，s；vψ为流体质点运动速度，m／s；k为储层平均渗透率，mD；μ为流体黏度，mPa·s；Swc为束缚水饱和度，%；Sor为残余油饱和度，%；φ为储层孔隙度，%；Sψ为运动距离，m；vψ为运动速度，m／d；t小质点运动时间，s；ψ为任意一条流线。

结果表明，随着裂缝长度的增加，见水时间逐渐增大。因此，在保障能形成有效驱替的条件下，适当拉长油水井之间的排距是有利的。

4 直井－压裂井网驱替效率

对于井网问题，若地层厚度为h，井距为2a，排距为b，定义储层井网单元驱替效率E为：当注入水突破时所扫过的井网单元体积2V占井网单元总体积4abh的百分数，即：

在稳定注水情况下，若忽略注入水的压缩性，根据物质守恒原理可知：

若进一步推演驱油效率定义式，则有：

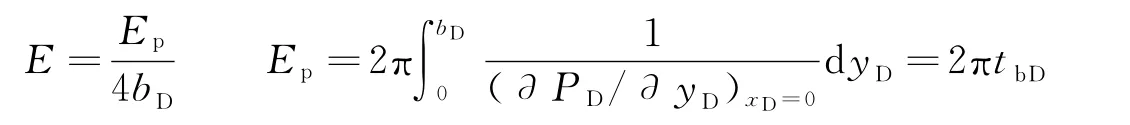
式中，B为体积系数；φ为储层孔隙度，%；2V为井网单元体积，m3；h为地层厚度，m；E为驱油效率，%。

显然驱油效率函数Ep与注入水突破时间是成正比的。因此，考察驱替效率问题其实质就是讨论无量纲注水突破时间问题。在井、排距给定的情况下，无量纲注水突破时间值就表明了驱替效率的大小。

裂缝越长，其驱油的效率越好，特别是当穿透比大于0.1以后，驱油效率与穿透比呈现近似线性关系。

5 直井－压裂井网见水后含水上升规律

当目标流场为许多形状不变的流管所分割后，平面渗流问题转化为沿流管的一维渗流问题。流线是从注入井始发的，将注入井的注入量平均地分配到每个流管中。倘若用N条流管（N条流线）分割目标流场， 由于在注采过程中最短流管中注入水最先到达生产井（生产井见水时间为tb），然后其他流管中的水依次到达，记在某一t时刻（t＞tb）相继有n（t）条流管中的注入水到达井底，那么此时含水率为：

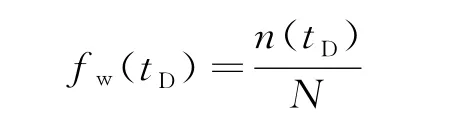
注入水突破时间为：

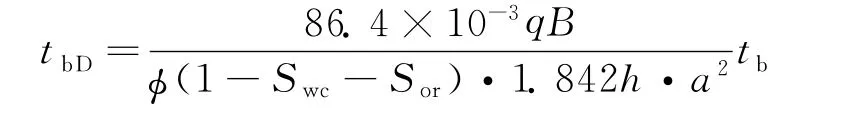
从上式计算结果得出，裂缝的存在是有利有弊的，随着裂缝长度的增大，会得到较高的初始产量，且引起无水采油期的延长，但同时，当水驱前沿进入井底会导致含水上升的速度加快，且产油量下降速度加快。

6 结论与建议

1）针对直井－压裂井混合布井问题，理论研究认为压裂后，在压裂裂缝周围的形成线性流流线，使得井筒附近渗流阻力变小，水驱前缘变得平缓，延长了无水采油期。

2）随着裂缝长度的增加，见水时间逐渐增大，其驱油效率越好，初始产量也较高，且引起无水采油期的延长，但当水驱前缘进入井底会导致含水上升的速度加快，且产油量下降速度加快，因此，方案优化时应予以考虑。

3）正对注水是引起高含水的主要原因。正对注水时，见水最快的主流线即为油水井之间的连线，如果油水井按照交替布井，在相同的井排距下，必然会延长主流线的长度，延长无水采油期。

［1］ 王建忠，姚军 .裂缝性低渗油藏试井模型与非稳态压力特征 ［J］.特种油气藏，2013，20（2）：69－71.

［2］ 郭大立，赵金洲，吴刚，等 .水力压裂优化设计方法 ［J］.西南石油学院学报，1999，21（4）：61－63.

［3］ 汤昌福，王晓冬，刘翰林，等 .聚合物驱流线模拟中的更新流线问题 ［J］.特种油气藏，2013，20（2）：75－78.

［4］ 许江文，郭大立，计勇，等 .压裂改造措施分析及优化技术 ［J］.大庆石油地质与开发，2011，30（5）：105－108.