浓差极化对震电耦合波传播的影响机制
2014-12-03张泉滢关继腾张小千
张泉滢,关继腾,张小千
(中国石油大学(华东)理学院,山东 青岛266580)
0 引 言
浓差极化现象在油气井中普遍存在。为了钻井安全,钻井过程中使用淡水泥浆,当泥浆滤液和地层水2种矿化度不同的液体相接触时,会发生各种电化学活动,形成自然电场,早期的自然电位测井就是在此基础上提出的。因此,浓差极化效应在测井中是不可忽视的影响因素。
利用震电效应进行测井具备了地震和电法测井两者的优点,引起国内外广泛关注[1-2]。1993年,Thompson等[3]首次对含流体地层进行震电勘探实验,初步验证了震电勘探具有高分辨率和选择性好的优点。Pride[4]采用体积平均法导出了多孔介质中电磁场和弹性波场耦合的宏观控制方程组,但是没有考虑溶液离子的扩散效应和(浓差极化)放大效应的影响。苏联学者波达波夫等[5]报道了室内、模型井以及野外震电试验结果,结果表明震电测井有良好应用前景。Mikailov[6]从Pride理论出发,提出了低频斯通利波激发极化电场的理论模型,将震电理论向井中实用化推进了一步,并提出了震电测井的初步思想。周成当等[7]完善了井中声激发极化电场理论,并研究了声电波场中的能量转换。胡恒山等[1-2]采用轴对称假设导出了井中点声源激发时井内、外声场和电磁场的表达式,在此基础上给出数值算例,说明转换电磁场的基本特性,分析了部分介质参数对声电转换波的影响。韩学辉等[8]总结前人经验,指出了井中震电勘探的特殊性,自行设计实验系统观察和探讨了直流电场对井液声学性质的影响。关威等[9]针对声电效应测井,分别计算了由单极声源、偶极声源、四极声源激发的井内声场及其诱导电磁场的全波波形。王莹等[10]开展了关于声电效应对自然电位测井曲线影响的研究,发现声波、侧向、自然电位并测时,自然电位曲线分辨率升高的现象是声波激发和侧向发射共同作用的结果。
考虑到井中浓差极化对震电效应影响的研究甚少,缺乏相关理论模型,不能进行定量描述与物理解释。本文基于Pride震电理论,建立了考虑浓差极化现象的震电耦合波控制方程组,开展相关的数值模拟;研究了浓差极化对震电横波、震电快纵波、震电慢纵波传播过程的影响机制。
1 Pride震电理论
假定谐变场的时间因子为e-iωt,得到均匀孔隙介质中震电耦合宏观控制方程[4]

式中,E、D、H、B和J分别表示电场强度、电位移矢量、磁场强度、磁感应强度和电流密度;τ表示应力张量;σ为动态电导率;ω为角速度;p是流体压强;L12为电动耦合系数;L21为动电耦合系数;κD为动态渗透率;η为流体黏度;μ为磁导率;φ是孔隙度;ρ是地层密度,可用基质密度ρs和流体密度ρf表示为ρ=(1-φ)ρs+φρf;w为渗流位移,可用固相位移u和液相平均位移uf表示,w=φ(uf-u);ε为孔隙介质介电常数,可用流体介电常数εf、基质介电常数εs表示为ε=φεf+(1-φ)εs;K、C、M、G分别为孔隙介质独立的弹性量。
根据文献[11]可以推导出震电横波、震电快纵波和震电慢纵波的电场强度E0与固相速度˙u0之比
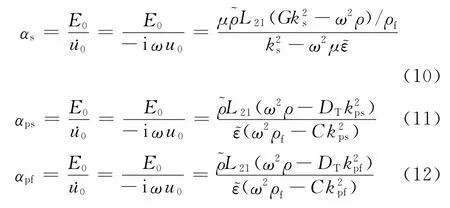
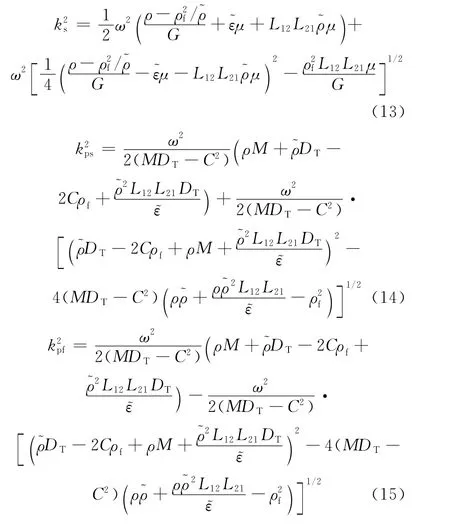
其中,C、DT、M、K的表达式为

式中,Ks、Kf分别代表固体基质体积模量和流相体积模量,为储层已知参数;G、Kb分别代表地层剪切模量和骨架体积模量,可以由复合介质弹性模量自洽理论确定。
电动耦合系数L12、动电耦合系数L21、动态渗透率κD和电导率σ具体表达式由文献[12]给出。
2 浓差极化效应对Pride震电方程的影响
传统的Pride震电理论没有考虑浓差极化现象,其认为地层水中离子浓度是均匀分布的。但是井中震电理论需要考虑浓差极化的影响,因为泥浆滤液和地层水离子浓度的巨大差异造成了地层溶液浓度的不均匀分布,使得地层中的某些参数发生了改变。针对以上问题,建立考虑浓差极化影响的震电耦合方程组。Pride震电方程是一组宏观平均控制方程组,浓差极化只会影响方程参数的宏观取值,不会改变其方程结构;因此只需要求出浓差极化存在时整个区域的参数平均值,替换原方程的参数即可。实际计算中,离子浓度对电动耦合系数L12、动电耦合系数L21、动态渗透率κD和电导率σ影响较大,对其他参数的影响可以忽略不计。因此,只需求整个区域的L12、L21、κD和σ平均值即可。
L12、L21、κD和σ平均值公式推导:假设地层水和泥浆滤液浓度分别为C1、C2,沿着浓差极化方向将介质N等分;令N足够大,那么每一段的离子浓度都可以看作均匀的。
对于第i段介质,其离子浓度Ci可表示

L12i、L21i、κDi和σi分别表示第i段介质的电动耦合系数、动电耦合系数、动态渗透率和电导率。根据文献[12]可知,第i段介质中的L12i、L21i、κDi和σi满足储层岩石电流场和渗流场耦合方程
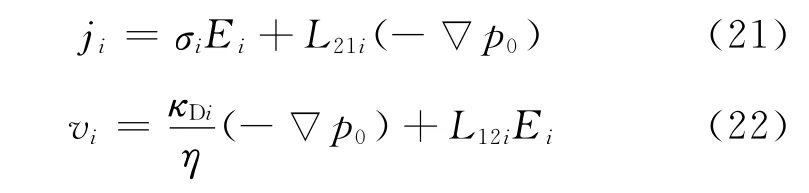
式中,p0为流体压力,与式(9)中的p不同,文献[12]忽略了固液两相相对运动的影响,认为整个介质中的p0是相等的;Ei、vi和ji分别表示第i段介质中的电场强度、渗流速度和电流密度。
结合式(21)和式(22),利用N段介质之间存在的联系,就能得到整个介质电参数平均值的表达式。值得注意的是,整个区域的L12、L21、κD和σ平均表达式并不是唯一的。当固相u运动方向固定时,浓差极化方向不同会造成N段介质之间的关系改变,最终导致整个区域电参数平均值改变。
2.1 浓差极化方向和u方向平行
当固相位移和浓差极化方向平行时,相当于波在N段浓度不同的串联介质中传播。串联介质的电压、电流和渗流速度满足U总=E1Δx+…+ENΔx=¯E(NΔx);j总=j1=…=jN=¯j;v总=v1=…=vN=¯v。结合式(21)和式(22)就可以得到N段介质满足的总关系式
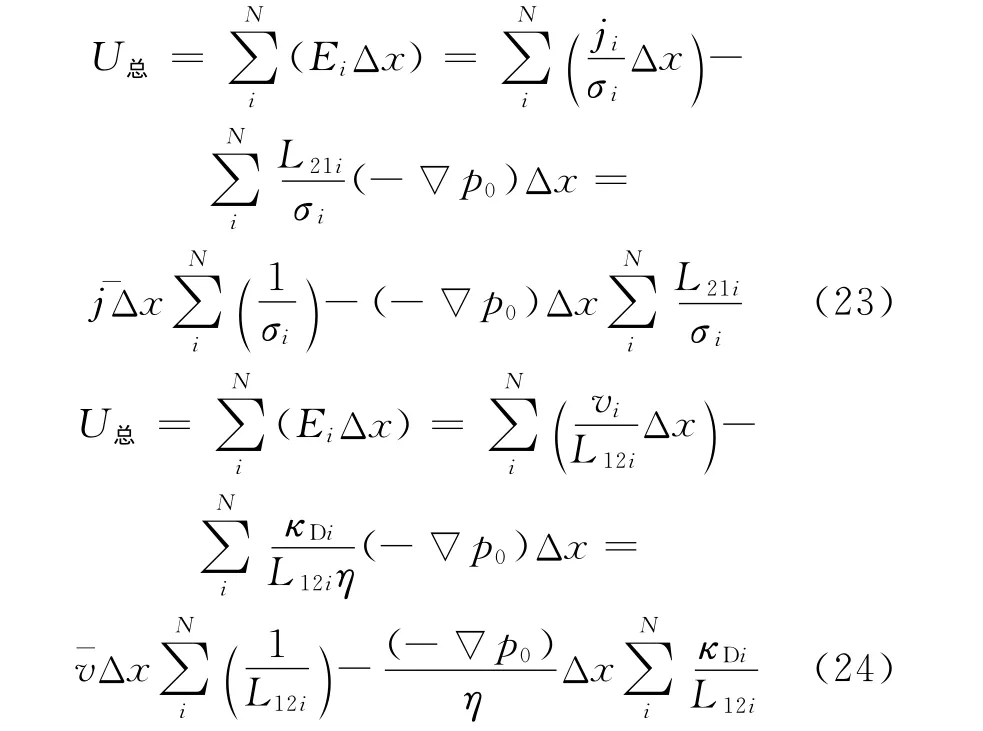
将式(23)、式(24)化简变形,得到
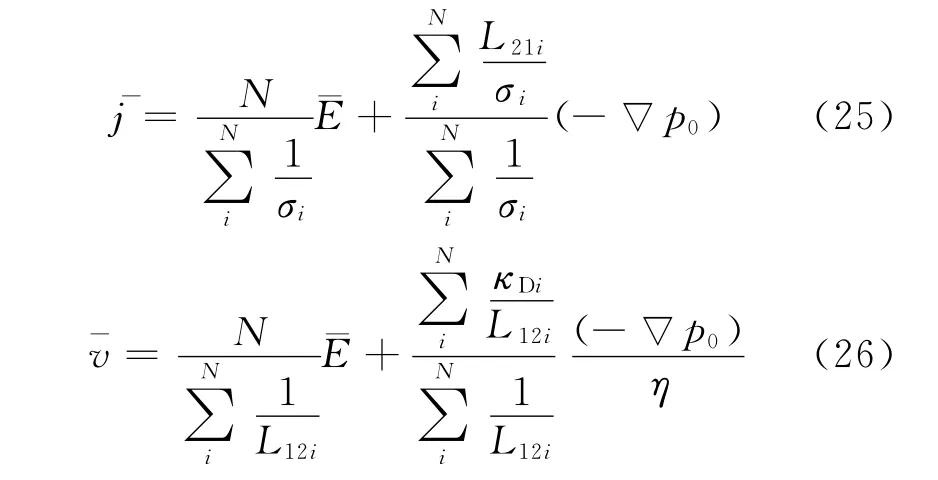
固相位移和浓差极化方向平行时,整个区域的L12、L21、κD和σ公式如下
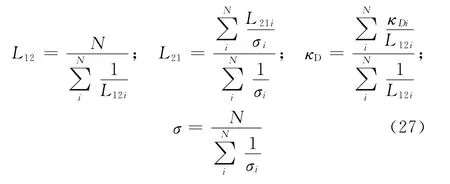
2.2 浓差极化方向与u方向垂直
u与浓度梯度方向垂直时,相当于波在N段浓度不同的并联介质中传播。并联介质中,各部分电压、电流和流速分别满足U总=U1=…=UN=(Δx);j总=j1+…+jN=N¯j;v总=v1+…+vN=。同理,得到整个区域的平均方程组
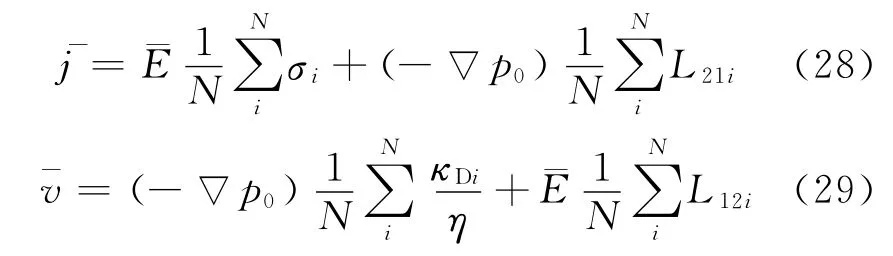
u与浓差极化方向垂直时,L12、L21、κD、σ表达式为
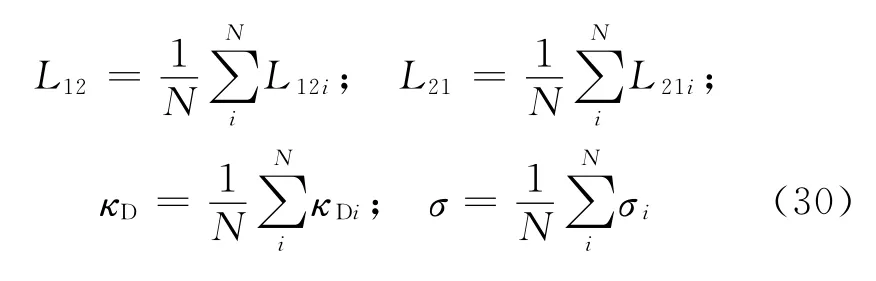
3 数值计算
浓差极化现象是钻井过程中注入的泥浆滤液和地层水矿化度不同引起井壁附近溶液浓度重新分布形成的。浓差极化对井中震电效应的影响,主要表现是物理场量的变化。数值模拟发现浓差极化现象对震电耦合波渗流速度、固相速度以及衰减常数等物理量影响甚微,对电场影响明显。因此,主要开展浓差极化对震电耦合波电场的影响,并研究浓差极化存在时,电场随着阳离子交换量和孔隙度的变化规律。
数值模拟需要选取基本地层参数。假定地层溶液为NaCl,孔隙度φ=0.20,温度T=298K,流体密度ρf=1 000kg·m-3,基质密度ρs=2 480kg·m-3,黏度η=0.001Pa·s,阳离子交换量QV=1.0 mol·L-1,Na+迁移率v+=50.1cm2·S·mol-1,Cl-迁移率v-=76.3cm2·S·mol-1真空介电常数ε0=8.85×10-12F·m-1,固体基质体积模量Ks=40.7GPa,流相体积模量Kf=2.2GPa,固体基质剪切模量Gs=29.7GPa,流相剪切模量Gf=0GPa,真空磁导率μ0=4π×10-7N·A-2,固体基质介电常数εs=4ε0,水的介电常数εf=80ε0。当浓度梯度和u的方向平行时,震电方程组中σ、L12、L21和κD应采用式(27)计算;当u的方向与浓度梯度方向垂直时,应选取式(30)。
3.1 浓差极化对震电波电场的影响
假定原始泥浆滤液矿化度C2为1 000mg·L-1,改变地层水矿化度C1的取值,其他取值参考基本地层参数,利用式(10)至式(12)计算震电耦合波电场强度与浓度差的关系。在该过程中,将泥浆滤液和地层水矿化度的平均值[即C0=(C1+C2)/2]作为不考虑浓差极化时的等效平均浓度。绘制出浓差极化与u方向平行、垂直以及取等效浓度时电场强度随浓差的变化曲线,以C1/C2为横坐标,对3条曲线比较(见图1)。图1(a)至图1(c)分别表示不同浓度差下,震电横波、震电慢纵波和震电快纵波电场强度与固相速度之比的模值,其中模数是浓度梯度的方向。
由图1可知,当地层水和泥浆滤液矿化度相等时,不存在浓差极化效应,3条曲线交于一点;随着浓度差的增大,3种震电波的电场强度与固相速度之比的模值明显减小。这是因为浓度差增大,意味着地层水矿化度增大,地层中每一点的浓度增大,双电层作用减弱,剩余电荷变少,形成的电场就会变小,模值减小。此外,浓度梯度方向也对震电波的电场有所影响;浓差与固相运动方向垂直时的电场模值要小于平行的状况,但是二者都大于等效平均浓度的状况;且随着浓度差增大,三者之间的差值开始变大。这就意味着当浓度差较大时,浓差极化现象在研究井中震电效应是不能忽略的,也不能简单地用等效平均浓度代替,需要考虑浓差极化大小和方向等问题。
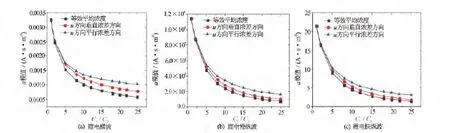
图1 浓差极化对震电波电场强度的影响
3.2 阳离子交换量对震电耦合波电场的影响
令泥浆滤液矿化度C2为1 000mg·L-1,地层水矿化度C1为10 000mg·L-1保持不变,改变阳离子交换量的取值,利用式(10)至式(12)数值模拟震电耦合波电场强度与阳离子交换量的关系(见图2)。图2(a)至图2(c)分别表示浓差极化作用下震电横波、震电慢纵波和震电快纵波电场强度随阳离子交换量的变化规律,其中模数是浓度梯度的方向。
阳离子交换量增大会导致双电层作用越强,地层水中的剩余电荷增多,形成的电场也会增强,正如图2所示,3种震电耦合波电场强度与固相速度之比的模值随着阳离子交换量的增大而增大。另外,随着阳离子交换量增大,等效恒定浓度得到的电场与另外2种方法得到的电场差距越来越大,但是3条曲线的电场大小关系依然保持不变。这表明在阳离子交换量较大的情况下,用等效平均浓度代替浓差极化效应不合理。
3.3 孔隙度对震电耦合波电场的影响
令泥浆滤液矿化度C2为1 000mg·L-1,地层水矿化度C1为10 000mg·L-1保持不变,改变孔隙度的取值,利用式(10)至式(12)数值模拟震电耦合波电场强度与孔隙度的关系(见图3)。图3(a)至图3(c)分别表示浓差极化作用下,震电横波、震电慢纵波和震电快纵波电场强度随孔隙度的变化规律,其中模数是浓度梯度的方向。
由图3可知,随着孔隙度的增大,震电横波和震电快纵波的电场强度与固相速度之比的模值增大,震电慢纵波模值减小。此外,随着孔隙度增大,震电横波和震电快纵波3条曲线电场差距增大,而震电慢纵波恰恰相反;但是3条曲线大小关系没有改变。
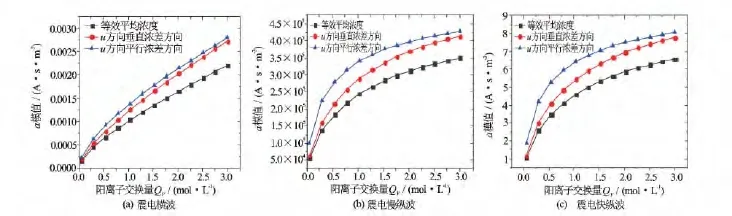
图2 阳离子交换量对震电波电场强度的影响
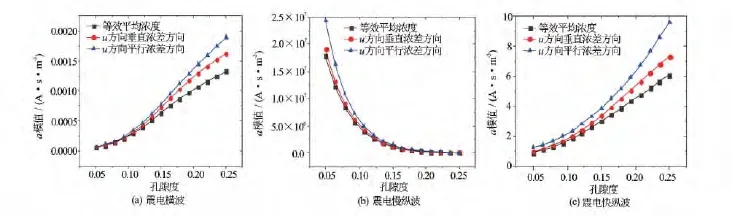
图3 孔隙度对震电波电场强度的影响
4 结 论
(1)在某些情况下(如浓差较大或阳离子交换量较大时),地层中的浓差极化现象是不能忽略或者利用简单的平均思想替代的,这样会引起很大的误差。利用Pride震电理论推导出考虑浓差极化效应的震电耦合控制方程组,定量研究了浓差极化现象对震电耦合波传播的影响。
(2)随着浓度差的增大和阳离子交换量的减小,3种震电波的电场强度与固相速度之比的模值减小。这是因为浓度差增大或者阳离子交换量的减小都引起了双电层作用的减弱,溶液剩余电荷变少,形成电场就会变弱。随着孔隙度的增大,震电横波和震电快纵波的电场强度与固相速度之比的模值增大,而震电慢纵波恰恰相反。
(3)浓差极化方向也对震电波电场有所影响。浓差与固相运动方向垂直时的电场模值小于平行的状况,但是二者都大于等效恒定浓度的状况。浓差、阳离子交换量和孔隙度不影响三者之间的大小关系,但是会改变三者电场的差值。
[1] 胡恒山,王克协.井孔周围轴对称声电耦合波:理论(I)[J].测井技术,1999,23(6):427-432.
[2] 胡恒山,李长文,王克协,等.声电效应测井模型实验研究 [J].测井技术,2001,25(2):89-95.
[3] Thompson A H,Gist G A.Geophysical Application of Electrokinetic Conversion [J].The Leading Edge,1993,12:1169-1173.
[4] Pride S R.Governing Equations for the Coupled Electromagnetics and Acoustics of Porous Media [J].Physical Review B,1994,50(21):15678-15696.
[5] 波达波夫O A,等.震电勘探原理 [M].裘慰庭,李乐天,译.北京:石油工业出版社,1996.
[6] Mikhailov O V.Electroseismic Investigation of the Shallow Subsurface:Field Measurements and Numerical Modeling[J].Geophysics,1997,62(1):97-105.
[7] 周成当,管志宁,严洪瑞,等.井中声电转换波场辐射能量定量分析 [J].地球物理学报,2001,44(4):563-572.
[8] 韩学辉,何亿成,楚泽涵,等.井中震电效应的模拟实验研究I:井液部分 [J].地球物理学进展,2004,19(2):399-403.
[9] 关威,胡恒山,储昭坦.声诱导电磁场的赫兹矢量表示与多极声电测井模拟 [J].物理学报,2006,55(1):267-274.
[10] 王莹,杨帆,马文中.声电效应对自然电位测井曲线的影响 [J].石油仪器,2013,27(1):60-62.
[11] Pride S R,Haartsen M W.Electroseismic Wave Properties[J].Journal of the Acoustical Society of America,1996,100(3):1301-1315.
[12] 于华,关继腾,陈辉,等.储层岩石流动电位频散特性的数学模拟 [J].地球物理学报,2013,56(2):676-687.
