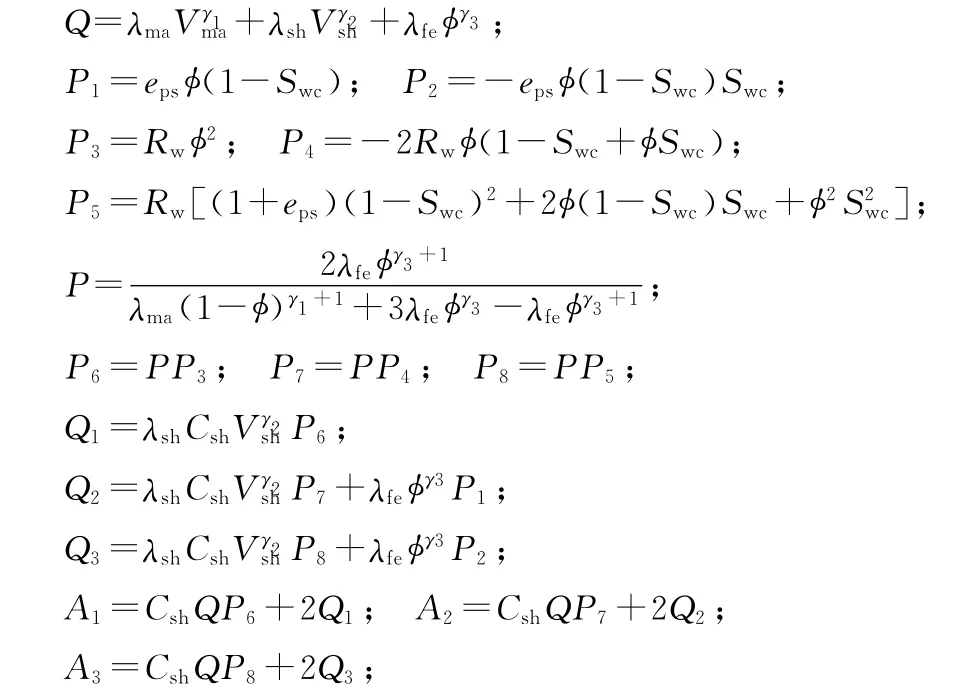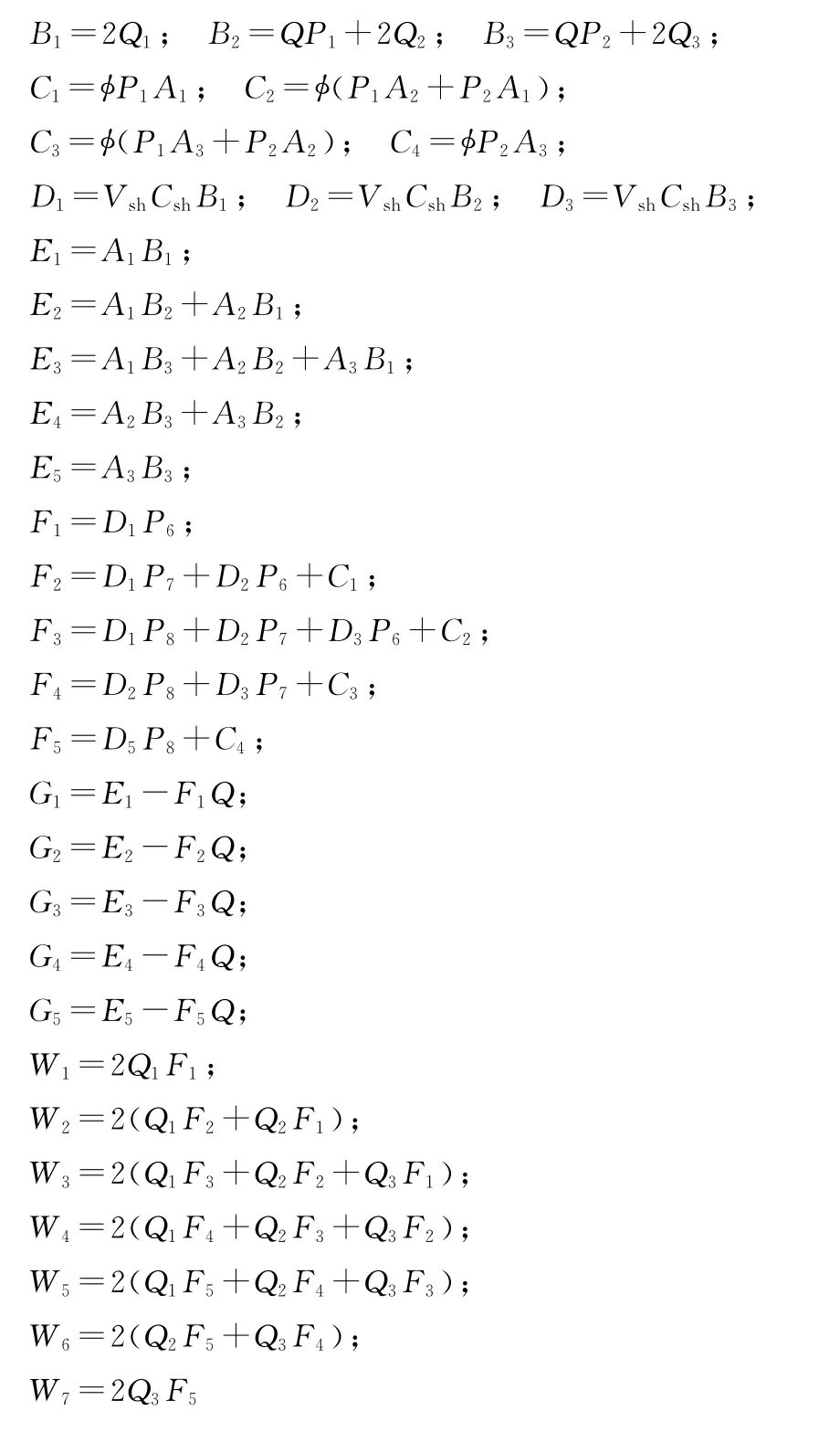基于有效介质与等效岩石元素理论的特低渗透率储层饱和度模型

宋延杰，杨汁，刘兴周，胡凯，唐晓敏

（1.东北石油大学地球科学学院，黑龙江 大庆163318；2.非常规油气成藏与开发省部共建国家重点实验室培育基地，黑龙江 大庆163318；3.中国石油辽河勘探开发研究院，辽宁 盘锦124010）

0 引 言

清水洼陷沙三段储层岩性主要以砂岩为主，其次为砂砾岩，矿物成分以石英为主，斜长石和钾长石次之，孔隙度主要分布范围为9.0%～18.0%，平均值为12.2%，渗透率主要分布范围为0.3～10.0mD＊非法定计量单位，1mD＝9.87×10－4μm2，下同，平均值为4.7mD，泥质含量分布在5.0%～17.0%的样品比例为69.1%，黏土矿物类型中伊蒙混层、伊利石、高岭石、绿泥石含量均较高，储层微孔隙体积（孔隙半径小于0.1μm的孔隙体积）占岩石孔隙体积百分比主要分布范围为45%～85%，平均值为59.7%，宏孔隙与微孔隙之比为0.5～1.4。因此，该区块沙三段储层属于特低渗透率储层，具有含泥质、微孔隙发育、束缚水饱和度较高、孔隙结构复杂的特征。据此在建立适用于该区块储层特征的导电模型时应考虑这些因素对岩石导电性的影响。

周荣安等［1－5］通过研究低孔隙度条件下地层因素F与渗透率、平均孔喉比、孔喉分选系数、结构系数等之间的关系建立了修正的阿尔奇公式，考虑了孔隙结构对岩石电性的影响，从而提高了孔隙结构复杂的低渗透率储层含水饱和度求取精度。张奉东等［6－8］在低孔隙度渗透率储层三水导电模型的应用中将微孔隙水与宏孔隙中的自由水分开，并用不同的胶结指数描述微孔隙水与自由水导电路径不同对岩石导电性的影响，考虑了孔隙结构对岩石导电性的影响，能较好地描述孔隙结构复杂的低渗透率储层导电规律。宋延杰等［9－10］采用有效介质对称导电理论描述低渗透率储层导电规律，在建立导电模型中为了考虑孔隙结构影响将微孔隙与宏孔隙分开，并引入了不同的渗滤指数和渗滤速率描述微孔隙水与宏孔隙中可动水的连通性、形状、导电路径不同对岩石导电性的影响，在低孔隙度低渗透率储层饱和度评价中取得了较好的应用效果。Winsauer等［11］将岩石孔隙体积简化为等截面积的弯曲毛细管，定义了一个表征孔隙弯曲迂回程度的变量——孔隙曲折度用来反映孔隙结构变化对岩石导电性的影响，从而给出了曲折度模型。曲折度的引入虽然将岩石电阻率和孔隙结构联系在一起，但将岩石孔隙体积简化为等截面积的弯曲毛细管较理想化。Herrick和Kennedy［12］将孔隙结构复杂的岩石的孔隙体积等效为弯曲且横截面积变化的毛细管，通过引入表征孔隙几何形态和孔隙中导电流体几何分布特征的2个参数，给出了孔隙几何形态导电理论，该理论更能反映孔隙几何形态及孔隙中导电流体分布状态对岩石导电性的影响。宋延杰等［13］针对低孔隙度低渗透率储层的孔隙结构特征，应用孔隙几何形态导电理论，将低孔隙度低渗透率储层岩石电导率看成黏土束缚水导电相、微孔隙水导电相和可动水导电相的等效电导率之和，考虑黏土束缚水孔隙、微孔隙、自由流体孔隙的孔隙几何形态以及自由流体孔隙中可动水的几何分布特征对岩石导电性影响，建立了低孔隙度低渗透率储层饱和度解释模型。Shang等［14－16］提出的等效岩石元素模型将纯岩石孔隙等效成小孔隙和大孔隙的串联，其中，大孔隙垂直于电势梯度，主要反映岩石孔腔大小，而小孔隙平行于电势梯度，主要反映岩石喉道大小，并新定义了孔隙结构效率定量描述这2种孔隙体积变化对岩石导电性的影响。该模型考虑了孔隙结构即孔喉比对岩石导电性的影响，从而可提高孔隙结构复杂的低渗透纯岩石饱和度计算精度。然而，目前尚未给出适用于泥质岩石的等效岩石元素模型。

本文针对清水洼陷沙三段储层含泥质、孔隙度渗透率低、孔隙结构复杂的特点，利用有效介质导电理论描述泥质对储层导电性的影响，利用等效岩石元素理论描述孔隙结构对储层导电性的影响，通过求取等效孔隙流体的电导率，将这2种理论结合在一起，从而建立一种新的基于有效介质与等效岩石元素理论的低孔隙度低渗透率储层饱和度模型，利用清水洼陷沙三段储层的岩电实验测量数据和测井资料，从实验精度分析及实际应用效果等方面评价模型在低孔隙度低渗透率储层中的适用性。

1 理论基础

1.1 有效介质对称导电理论

对于由体积含量为φ1，φ2，…，φn和电导率为C1，C2，…，Cn组成的n组分的混合介质，其混合介质的电导率Ct可以表示为［17－18］

式中，Cog为虚介质电导率，S／m。

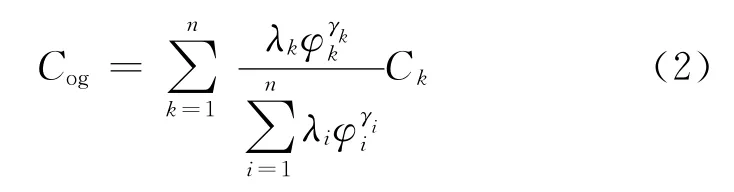
式中，渗滤速率λk反映岩石中第k种成分的连通状况；渗滤指数γk反映岩石中第k种成分形状和结构。

1.2 等效岩石元素理论

等效岩石元素模型将含水纯岩石孔隙空间等效成小孔隙和大孔隙的串联，其等效体积模型见图1［14］。其中，大孔隙体积为VLP，主要反映岩石孔腔大小；小孔隙体积为VSP，主要反映岩石喉道大小。引入孔隙结构效率eps表示小孔隙体积与大孔隙体积比。图2给出了含水纯岩石等效岩石元素模型的等效电路图。根据图2可推出含水纯岩石地层因素F表达式为

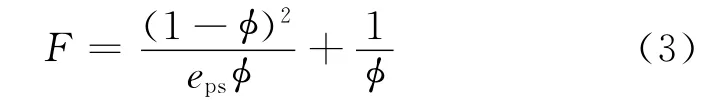
式中，φ为有效孔隙度，小数。

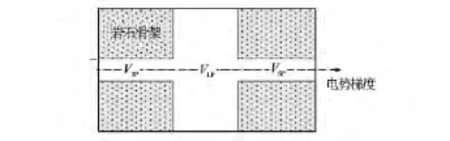
图1 饱含水纯岩石等效岩石元素模型的体积模型［14］

图2 饱含水纯岩石等效岩石元素模型的等效电路

令VLP＝1，由孔隙结构效率的定义可知VSP＝eps。对于含油气纯岩石，假设地层水均匀分布，则大孔隙体积中的含水体积VLPW和小孔隙体积中的含水体积VSPW随含水饱和度Sw减小而成比例减小，即有VLPW＝Sw，VSPW＝epsSw，其等效体积模型见图3。然而，由于孔隙尺寸与连通性、流体特性、矿物成分、颗粒润湿性等因素的影响，水在孔隙中并非均匀分布，因此，引入比例因子r反映小孔隙体积中含水体积和大孔隙体积中含水体积的非均匀分布，即有VSPW＝epsSwr。由VLPW＋VSPW＝Sw＋epsSw得VLPW＝［1＋（1－r）eps］Sw。根据孔隙结构效率定义，可得含油气纯岩石的水孔隙结构效率epsw为

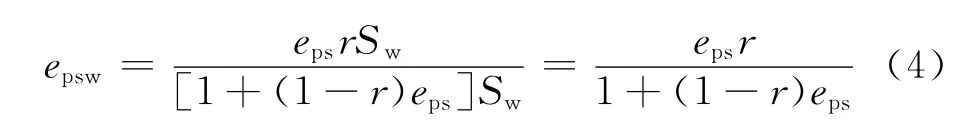
图4给出了含油气纯岩石等效岩石元素模型的等效电路图。根据图4可推出含油气纯岩石视地层因素Fw表达式为

图3 含油气纯岩石等效岩石元素模型的体积模型［14］

图4 含油气纯岩石等效岩石元素模型的等效电路

考虑临界含水饱和度Swc（水在孔隙中呈连续分布且导电的最小含水饱和度）的影响，引入有效含水饱和度S′w概念。S′w的表达式为

用S′w代替式（5）中Sw，可得考虑临界含水饱和度影响的含油气纯岩石视地层因素Fw表达式为

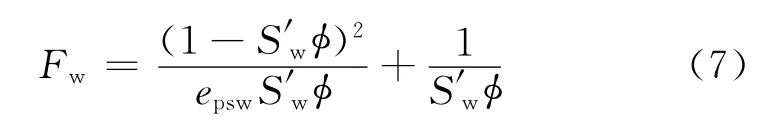
在相同测量条件下可认为临界含水饱和度近似等于束缚水饱和度，因而可用束缚水饱和度取代临界含水饱和度。

2 低渗透率储层导电模型

2.1 建模思路

在建立该区块储层导电模型过程中，首先可将储层中的泥质看成不导电骨架的一部分，并认为孔隙体积大小、形状、连通性和油气水含量及分布状况不发生变化，从而给出等效纯岩石（体积模型见图5）。对于该等效纯岩石，分别利用有效介质对称导电理论和等效岩石元素理论描述由岩石骨架和孔隙（由油气和水2个部分组成的混合流体介质）2组分组成的纯岩石的导电规律，令求得的2个纯岩石电导率相等，从而得出等效混合流体介质电导率表达式；然后，利用有效介质对称导电理论描述由岩石骨架、泥质及孔隙三组分组成的含泥低渗透率岩石的导电规律，并用求得的纯岩石等效混合流体介质电导率取代研究区含泥低渗透率岩石混合流体介质电导率，在此基础上建立适用于该区块含泥低渗透率储层的导电模型。

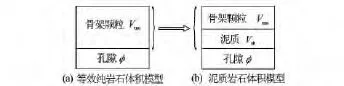
图5 含泥低渗透率储层等效体积模型

2.2 确定混合流体介质电导率

2.2.1 等效岩石元素模型计算纯岩石电导率

由Fw＝Rt1／Rw以及式（6）和式（7）可推导出纯岩石的电导率表达式

式中，Rw为地层水电阻率，系数P1、P2、P3、P4、P5的表达式见附录。

2.2.2 有效介质导电模型计算纯岩石电导率

对于2组分组成的纯岩石其体积模型见图5（a）。由于骨架颗粒不导电，故骨架颗粒电导率Cma＝0，由式（1）可知

式中，φ为纯岩石的有效孔隙度，小数；Cfe为纯岩石等效混合流体电导率，S／m。整理式（9）可得

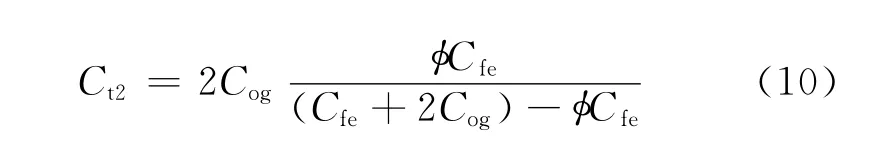
由式（2）可得虚介质电导率Cog的计算公式为

式中，λma、λfe分别为岩石骨架、混合流体的渗滤速率；γ1、γ3分别为岩石骨架、混合流体的渗滤指数。

将式（11）代入式（10），得出纯岩石电导率Ct2

2.2.3 等效混合流体电导率的求取

联立式（8）和式（12），并令Ct1＝Ct2，可得到等效混合流体电导率的表达式为

2.3 含泥低渗透率岩石导电模型的建立

针对清水洼陷沙三段砂岩储层的特征，认为研究区储层岩石由不导电的砂岩骨架颗粒、泥质以及混合流体介质3种组分组成，其体积模型见图5（b），其物质平衡方程为

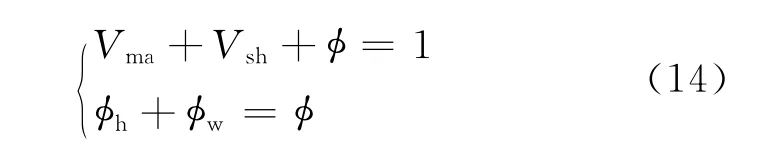
式中，Vma、Vsh分别表示泥质砂岩的骨架颗粒体积含量、泥质体积含量，小数；φh、φw、φ分别代表泥质砂岩的含油气孔隙度、含水孔隙度、有效孔隙度，小数。

由式（1）可知

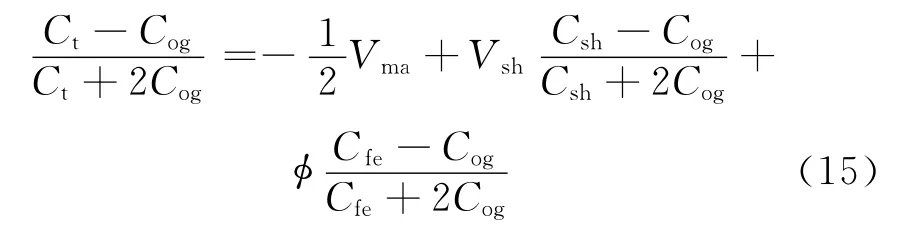
整理式（15）得

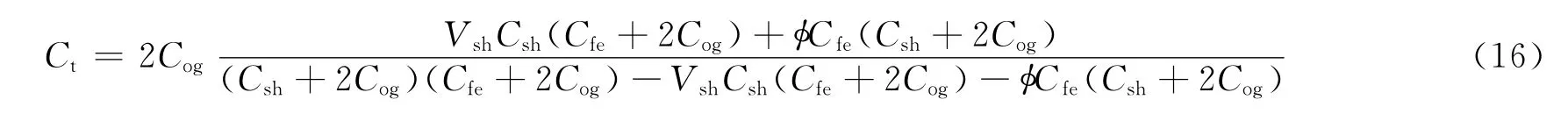
由式（2）可得虚介质Cog的计算公式为

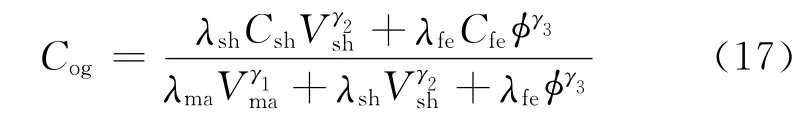
式中，λma、λsh、λfe分别为泥质砂岩中岩石骨架、泥质、等效混合流体的渗滤速率；γ1、γ2、γ3分别为泥质砂岩中岩石骨架、泥质、等效混合流体的渗滤指数。

将式（13）、式（17）代入式（16），整理得

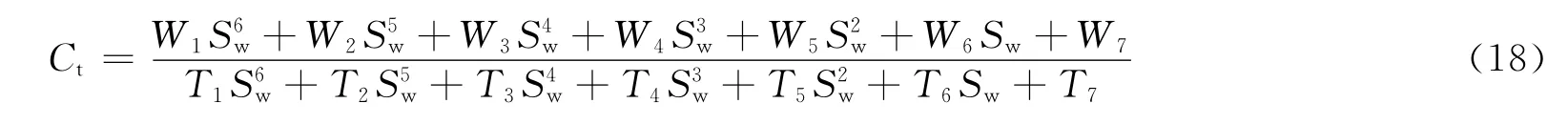
式中，系数W1～W7和T1～T7的表达式见附录。方程（18）即为清水洼陷沙三段低渗透率储层导电模型。

3 模型实验验证

利用清水洼陷沙三段2口井的17块岩样的岩电实验数据，令λma＝1.0，γ＝γ1＝γ3，采用最优化方法求解Ct－Cw－Sw的非相干函数，可得到epsw、γ、γ2、λsh、λfe值。将优化的参数代入建立的导电模型中，计算出每块岩样不同含水饱和度的岩石电导率值。图6给出了部分岩样导电模型计算岩石电导率值与岩心测量值对比图。从图6中可以看出，计算岩样电导率与测量岩样电导率吻合很好，测量岩样电导率Ct与计算岩样电导率Ctc的平均相对误差为3.6%，误差很低，说明本文给出的模型可以描述清水洼陷沙三段低渗透储层的岩石导电规律。

图6 部分岩心电阻率与计算电阻率对比图

4 实际应用效果评价

4.1 确定模型参数

根据17块岩样计算的epsw、泥质渗滤速率λsh、泥质渗滤指数γsh、混合流体渗滤速率λfe、混合流体或骨架渗滤指数γ与孔隙度的交会图分析可以得出，epsw、λsh、γsh、λfe、γ与孔隙度无明显关系，且数值变化较小，故可以使用由实验测量数据求得的epsw、λsh、γsh、λfe、γ的平均值作为该地区沙三段低渗透率储层的epsw、λsh、γsh、λfe、γ值。其实用值为epsw＝0.085，λsh＝0.818，γsh＝0.749，λfe＝0.200，γ＝1.799。

4.2 应用实例

利用本文建立的储层饱和度模型对清水洼陷沙三段的A井进行处理，并将解释结果与试油结果进行对比。该井解释成果图见图7。该井处理的3 303.1～3 313.1m为试油井段，即52号层及53号层的上部，日产气1 450m3，日产油4.53t，日产水2.16m3，试油结论为油水同层。由本文建立的模型处理结果可知，52号层孔隙度为14.2%，渗透率为3.2mD，孔渗较好，含水饱和度为55.2%，解释为油层；53号层孔隙度为12.3%，渗透率为1.2mD，含水饱和度为70.0%，解释为油水同层，与试油结论相符。

5 结 论

（1）针对清水洼陷沙三段储层含泥质、孔隙结构复杂的特点，引入了等效岩石元素理论和有效介质导电理论描述孔隙结构即孔腔和喉道比和泥质附加导电对储层导电性的影响。利用等效岩石元素理论描述孔腔和喉道比对储层导电性的影响，利用有效介质导电理论描述泥质对储层导电性的影响。

（2）将含泥特低渗透率储层等效成孔隙及所含流体不变的纯岩石，采用有效介质对称导电理论和等效岩石元素理论建立由岩石骨架和孔隙（混合流体介质）2组分组成的纯岩石的导电方程，联立求解即可得出等效混合流体介质电导率表达式。采用有效介质对称导电理论建立由岩石骨架、泥质及孔隙（混合流体介质）3组分组成的含泥特低渗透率岩石的导电方程，并代入求得的等效混合流体介质电导率，从而建立了基于等效岩石元素理论和有效介质对称导电理论的含泥特低渗透率储层导电模型。

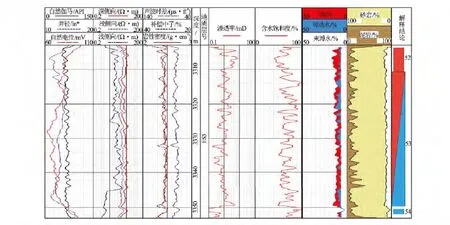
图7 清水洼陷沙三段储层A井测井解释成果图

（3）通过岩电实验测量数据的验证，表明本文提出的模型能很好地描述特低渗透率储层岩石的导电规律。实际应用结果表明基于有效介质与等效岩石元素理论建立的饱和度模型确实能够提高特低渗透率储层饱和度的解释精度。

［1］ 周荣安.阿尔奇公式在碎屑岩储集层中的应用 ［J］.石油勘探与开发，1998，25（5）：80－82.

［2］ 李秋实，周荣安，张金功，等.阿尔奇公式与储层孔隙结构的关系 ［J］.石油与天然气地质，2002，23（4）：364－367.

［3］ 李潮流，李长喜.特低渗透率砂岩储集层电学性质研究 ［J］.测井技术，2010，34（3）：233－237.

［4］ 宋延杰，王楠，唐晓敏.曲折度电阻率模型在大庆G地区低渗储层评价中的应用 ［J］.地球物理学进展，2012，27（5）：2008－2015.

［5］ Klaas Verwer，Gregor P Eberli，Ralf J Weger.Effect of Pore Structure on Electrical Resistivity in Carbonates［J］.AAPG Bulletin，2011，95（2）：175－190.

［6］ 张奉东，潘保芝.三水模型在腰英台油田储层测井解释中的应用 ［J］.世界地质，2009，28（2）：226－232.

［7］ 张丽华，潘保芝，李舟波，等.新三水导电模型及其在低孔低渗储层评价中的应用 ［J］.石油地球物理勘探，2010，45（3）：431－435.

［8］ 张丽华，潘保芝，李宁，等.基于三水模型的储层分类方法评价低孔隙度低渗透率储层 ［J］.测井技术，2011，35（1）：31－35.

［9］ 宋延杰，韩建强，王瑛，等.考虑黏土连续性影响的低孔隙度低渗透率砂岩储层导电模型研究 ［J］.测井技术，2010，34（3）：205－209.

［10］ 宋延杰，王海琦，唐晓敏，等.南海东部低孔低渗储层测井评价方法 ［J］.大庆石油学院学报，2010，34（6）：106－110.

［11］ Winsauer W O，Shearin J H M，Masson P H，et al.Resistivity of Brine－saturated Sands in Relation to Pore Geometry［J］.AAPG Bulletin，1952，36（2）：253－277.

［12］ Herrick D C，Kennedy W D.A New Look at Electrical Conduction in Porous Media：A Physical Description of Rock Conductivity［C］∥The SPWLA 50th Annual Logging Symposium，June 21－24，2009，paper BB.

［13］ 宋延杰，王晓勇，唐晓敏.基于孔隙几何形态导电理论的低孔隙度低渗透率储层饱和度解释模型 ［J］.测井技术，2012，36（2）：124－129.

［14］ Shang B Z，Hamman J G，Caldwell D H.A Physical Model to Explain the First Archie Relationship and Beyond［C］∥SPE Annual Technical Conference and Exhibition，Denver，Colorado，U S A.，5－8October，2004，4.

［15］ Shang B Z，Hamman J G，Caldwell D H.Improved Water Saturation Estimation Using Equivalent Rock Element Model and Application to Different Rock Types［C］∥SPE Europec／EAGE Annual Conference and Exhibition，Rome，Italy，9－12，June，2008.

［16］ 葛新民，范宜仁.海塔盆地复杂岩性储层测井评价方法研究 ［D］.东营：中国石油大学（华东），2010.

［17］ Koelman J M V A，De Kuijper A.An Effective Medium Model for the Electric Conductivity of an N－component Anisotropic Percolating Mixture［J］.PHYSICA A，1997，247：10－22.

［18］ De Kuijper A，Sandor R K J，Hofman J P，et al.Electrical Conductivities in Oil－bearing Shaly Sand Accurately Described with the SATORI Saturation Model［J］.The Log Analyst，1996：22－31.

附录