考虑机器检修的圆钢热轧批量调度算法
2014-12-02许绍云李铁克王柏琳董广静
许绍云,李铁克,王 雷,王柏琳,柏 亮,董广静
(1.北京科技大学 东凌经济管理学院,北京 100083;2.北京科技大学 钢铁生产制造执行系统技术教育部工程研究中心,北京 100083;3.中国刑事警察学院 治安学系,辽宁 沈阳 110854)
0 引言
热轧批量调度是钢铁企业生产管理的一个重要任务,是根据热轧工序中相应的生产约束和规则对生产订单或原料钢坯进行组合形成轧制批,并对轧制批排定先后加工顺序,从而确定各自的加工时间的过程。由于热轧生产过程具有较高的复杂性,热轧批量调度的好坏对企业的生产效率和产品的质量具有关键性的影响,因此,有效的热轧批量调度对提高企业生产效率、增强企业市场竞争力具有重要的意义。
现有的关于热轧批量调度的研究,根据产品种类主要分为热轧带钢批量调度、热轧钢管批量调度、棒线材(热轧圆钢)批量调度等。热轧带钢作为钢铁企业的主要产品,其批量调度问题受到最广泛的关注,文献[1]将热轧批量问题归结为带软时间窗的车辆路径问题,通过建立单目标的约束满足模型实现问题的求解;文献[2]考虑热轧批量计划与炼钢连铸批量计划的协调性,提出一体化批量计划编制策略,并采用约束满足算法对问题进行求解;文献[3]将热轧批量调度问题归结为多路径问题,并提出一种基于精确算法和启发式算法的混合算法对问题进行求解;文献[4]将问题分为选坯、组批、排序三个过程,建立基于奖金收集车辆路径问题(Prize Collecting Vehicle Routing Problem,PCVRP)的多目标优化模型,并分别采用基于分解策略和Pareto最优的蚁群算法对问题进行求解。热轧钢管作为一类重要的经济型钢材,由于其热轧工艺的复杂性,其批量调度问题的研究具有重要的意义[5-7],问题的研究主要以订单为基本组织单元,求解过程主要分为组批和轧批排序两个阶段,问题优化对象主要是批次之间的转产调整时间和调整费用。对于在钢铁企业中普遍存在的棒线材(热轧圆钢)产品,由于在生产组织方式上与热轧钢管具有一定的相似性,其热轧批量调度问题同样考虑将订单组合为轧制批,批量排序时考虑批次间的调整时间[8],问题通常被归结为调整时间与加工顺序有关的调度问题进行求解,在制定调度计划时使总的调整时间和费用最少[9]。
本文根据圆钢热轧生产的特点,在以往研究的基础上,针对轧制批量排序阶段,考虑生产过程中存在的机器检修维护的情况,建立热轧工序轧制批量调度的多目标整数规划模型;结合问题特征,提出改进的带精英策略的快速非支配排序遗传算法(Nondominated Sorting Genetic Algorithm Ⅱ,NSGA-Ⅱ)进行求解;最后通过数据实验验证模型和求解算法的可行性和有效性。
1 问题建模
1.1 问题描述
圆钢热轧生产过程的一个显著特点在于轧制不同规格的产品需要不同的机架,这也意味着轧制不同规格的订单时需要进行机器调整,这一特征致使圆钢在热轧生产中需要采取批量成组加工方式,即将同类(同规格、同钢种等)的订单组合成轧制批进行生产,以保证生产的高效连续性。此外,在机器调整过程中,拆装机架的时间不同,导致不同批量的加工顺序可能会具有不同的机器调整时间,因此,在制定批量调度计划时需要考虑批量加工顺序对机器调整时间的影响。由此可见,圆钢热轧批量调度问题可以归结为一类带有实际生产约束的具有顺序依赖调整时间的批调度问题(Batch Scheduling Problem with Sequence-dependent Setup Time,BSPSST)。
在制定圆钢热轧批量调度优化方案时,根据其生产管理的特点和需求,主要考虑以下优化目标:
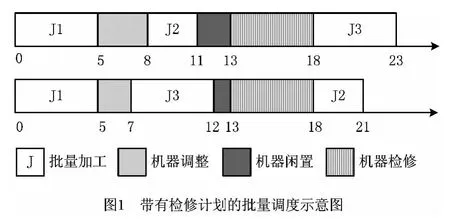
(1)产能利用率最大化 产能利用率在这里是指除机器检修和机器调整时间外的剩余计划期间内机器的使用情况,通过加工与检修时间差来衡量,加工和检修两者的时间差是由机器检修情况决定的。在实际生产中,机器需要定期进行检修维护,因此批量只允许在检修维护时间之外的计划期间内排产。为保证批量加工的连续性,规定批量不能跨越检修计划进行加工,这样就造成了批量加工过程和检修过程之间具有不能衔接的时间差,且不同的批量加工顺序产生的时间差大小不同。时间差的存在会造成产能资源的浪费,因此,制定调度计划时需要将该时间差作为优化目标。图1是对三个批量J1,J2和J3的调度示意图,机器闲置时间即为加工和检修两者的时间差,从图中可以看出,不同的批量加工顺序产生的机器调整时间和机器闲置时间不同,使得最终的完工时间不同,批量顺序J1,J3和J2要比J1,J2和J3具有更高的产能利用率。
(2)机器调整时间最小化 在圆钢轧制过程中,若频繁切换产品规格,会产生较多的机器调整时间,使得生产周期延长,造成生产效率降低。因此,制定调度计划时,应尽可能地将同规格的批量集中轧制,且对不同规格的批量确定有效的轧制顺序,最大限度地减少机器调整时间,提高生产效率。
(3)所有被调度的订单的交货提前和拖期时间最小化 订单在轧制过程中以批量的形式提交,在订单的管理过程中,企业在接受订单的同时向客户承诺了产品交货期,因此每个订单需要尽量在承诺的交货期内进行交货,若订单完成时间早于交货期,则会在货物等待发运的过程中造成相应的库存成本,若订单完成时间晚于交货期,则会使企业的信誉降低。因此,批量调度中需要考虑交货期的影响,尽可能地减少订单提前或拖期的时间。
根据实际生产的特点,问题存在的约束条件具体有:①由于进行调度的批量是经过核算后确定在当前计划期间内加工的,调度后最后一个批量的完工时间不能大于计划期间的末端时刻;②同种规格的批量之间的顺序必须遵循钢种的优先级顺序;③同一批量加工过程中不允许中断,即不能跨越机器检修期间,不能插入其他批量进行加工;④某一时刻,机器只能加工一个批量,不允许多个批量同时进行加工。
1.2 问题模型
(1)符号定义


(2)变量定义

(3)数学模型
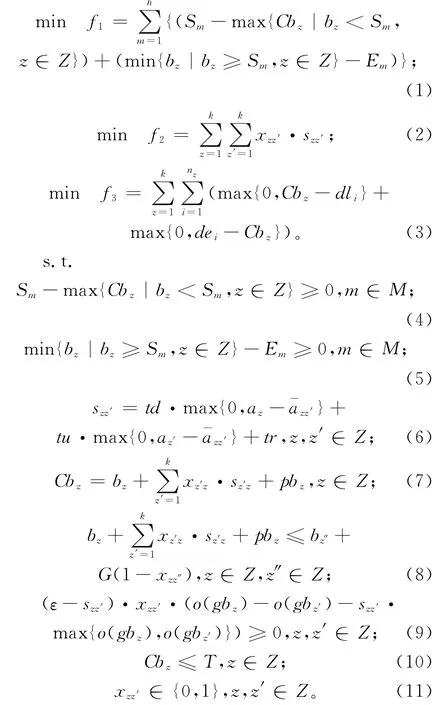
其中:目标函数(1)表示最小化机器加工与检修之间的时间差;目标函数(2)表示最小化机器总的调整时间;目标函数(3)表示最小化订单的提前和拖期总时间,其中,订单的完工时间取订单所在批量的完工时间;约束(4)和约束(5)表示批量加工过程不能跨越检修计划;约束(6)定义了相邻批量之间的机器调整时间;约束(7)定义了批量的完工时间;约束(8)表示两个相邻批量之间的加工顺序关系,同一时刻机器只能加工一个批量,且批量加工过程连续,不可中断插入其他批量;约束(9)表示规格相同的两个相邻批量之间加工先后顺序要满足钢种的优先级关系,即先加工的批量的钢种优先级不能低于后加工的批量的钢种优先级;约束(10)表示批量的完工时间不能晚于计划期的末端时刻;约束(11)为变量取值约束。
2 求解算法
由问题模型可以看出,考虑机器检修的圆钢热轧批量调度问题是一类具有多目标、多约束条件的排序优化问题,具有NP难的特性,精确算法难以在可行的时间内求得有效解。此外,解决多目标的优化问题需要对相互冲突的子目标进行综合考虑,协调各个目标间的冲突值,使得问题的求解变得更加困难。NSGA-Ⅱ[10]是Deb于2000年在非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm,NSGA)的基础上提出的,具有运行速度快、解集收敛性好的优点,由于它在种群规模、操作概率等模糊或明确的参数方面没有固定的要求,被广泛应用于实际项目中的多目标问题的求解。NSGA-Ⅱ在NSGA 的基础上主要针对如下三个方面进行了改进:
(1)采用快速非支配排序,降低算法的计算复杂度。
(2)提出拥挤度的概念,确定个体之间的紧密程度,为快速排序后的同级比较提供依据,使准Pareto域中的个体扩展到整个Pareto域并均匀分布,保持了种群的多样性。
(3)引入精英策略,扩大采样空间,将父代种群与子代种群组合,共同竞争产生下一代种群,保证了种群个体的优良性。
对本文所考虑的问题,采用NSGA-Ⅱ算法求解时主要解决的问题包括:编码规则的设计、适应度函数的定义及计算、初始解的生成、选择策略及精英策略的确定、遗传操作方式的选择等;此外,由于本文问题具有复杂的约束条件,基本的NSGA-Ⅱ算法在产生初始种群和迭代过程中并不能保证所有个体的可行性,从而可能得不到最终有效的求解结果。为此,本章提出改进的NSGA-Ⅱ算法(Modified Nondominated Sorting Genetic Algorithm Ⅱ,MNSGA-Ⅱ)以实现问题的有效求解。
2.1 编码规则
轧制批量调度主要是确定轧制批的加工先后顺序和加工时间,其解的构成即是一系列轧制批量构成的序列。算法采用十进制的自然顺序排列的批量顺序来表示染色体。
例如,对于由10 个批量构成的批量集合Z={1,2,3,4,5,6,7,8,9,10},若批量的加工顺序为1→3→4→2→8→5→7→6→10→9,则其编码为x=[1,3,4,2,8,5,7,6,10,9]。
2.2 种群初始化
基本的NSGA-Ⅱ初始解都是随机产生的,而随机生成的初始种群会存在违反约束条件的不可行解,且即使在可行的情况下也无法保障解的质量。本算法在初始阶段,利用改进的NEH 算法(Modified NEH,MNEH)产生局部满意的初始解,为了保证初始种群的多样性,MNEH 在基本的NEH 算法的基础上,通过不同的初始排序规则形成不同的染色体。由于本文问题具有多目标的特性,与经典的NEH 算法依据单适应度函数值逐步优化的方式不同,这里采用了文献[11]中提出的变权重组合法,采用随机权重的方式将问题的多个目标构造成单目标的适应度函数,如下:
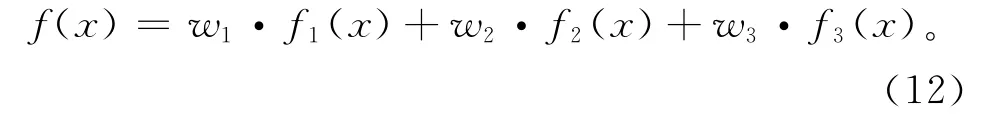
式中w1,w2,w3≥0。
采用MNEH 算法产生popSize个初始解的具体步骤如下:
算法1 MNEH 算法。
步骤1 正向NEH 产生第一条染色体。
步骤1.1 按照批量在所有工序上的总加工时长由大到小的顺序,对k个批量进行初始排序。
步骤1.2 随机生成三个权重系数w1,w2和w3,取前两个批量调度,根据式(12)计算适应度值并选择适应度值最小的批量顺序。
步骤1.3 令z从3~k变化,z每增加一个值,就随机生成三个权重系数w1,w2和w3,在不改变序列中z-1个批量先后顺序的条件下,将第z个批量插入当前序列中z个可能的位置,计算z插入每个位置后形成的批量序列对应的适应度函数值,最后选择具有最小适应度函数值的序列;重复此过程,获得使k个批量具有最小适应值的序列。
步骤1.4 将得到的具有最小适应度函数值的序列经过编码形成染色体。
步骤2 反向NEH 产生第二条染色体。
与步骤1相似,只是在初始排序时按照批量总加工时长由小到大的顺序进行排序。
步骤3 改进的正向NEH 产生剩余的popSize-2条染色体。
每生成一个染色体,改进正向NEH 的初始排序规则,即任选两个批量作为初始序列的前两个批量,剩余的k-2个批量按照加工时长由大到小的顺序排序,其他步骤同步骤1.2~步骤1.4。
2.3 适应度函数设计与种群修复
NSGA-Ⅱ在搜索进化过程中根据适应度函数值来评价个体的优劣,是非支配排序的度量依据,对算法进化的方向起指导作用。由于模型具有多目标、多约束条件的特征,为保证种群进化过程中子代个体的可行性,对适应度函数进行相应的设计,采用惩罚函数的思想,将部分关键的约束条件以惩罚值的形式加入目标函数中,构造适应度函数:
规则1 对重复个体x1=x2=…=xk′,保留一个个体x1不变,其他个体经过变异形成新个体,为保证个体与原解的相近性,变异采用交换个体中任意两个基因位置的方式,所有的重复个体更新为x1←x1,x2←Mut(x2),…,xk′←Mut(xk′),Mut(xi)为任意交换xi中两个基因的位置。
规则2 对不可行个体,或直接进行修复转化为可行解,或淘汰并由种群中其他个体的变异代替。对不可行个体x=(x1,x2,…,xn)的修复操作如下:
(1)若f2(x)<0,则说明该个体违背约束(10),淘汰x,选择种群中其他某个个体x′≠x,令x←Mut(x′);
(2)若f3(x)<0,则说明个体x违背约束条件(9),直接对x进行修复,确定个体x中满足条件o(gxi)<o(gxi+1)∧sxixi+1=0 的相邻分量xi,xi+1,交换xi,xi+1的先后顺序,重复寻找满足条件o(gxi)<o(gxi+1)∧sxixi+1=0 的相邻分量并交换先后顺序,直到不存在任意两个相邻分量违背钢种优先级关系。
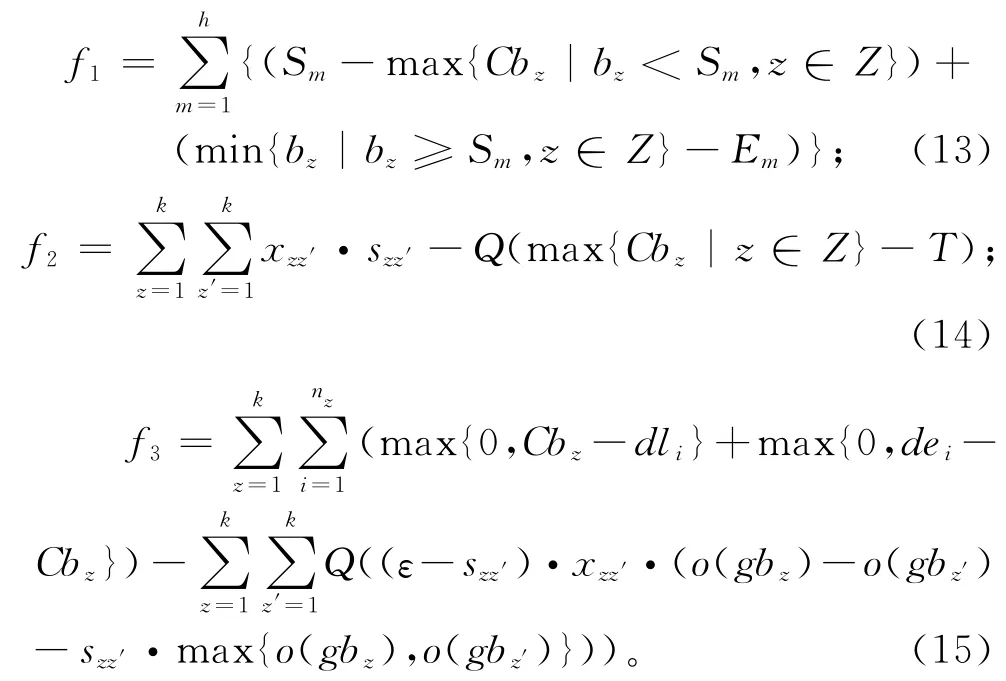
2.4 加工时间计算
式中Q是一个足够大的正数。
通过适应度函数的定义可以看出,对于种群中的任何一个个体,只要个体内的批量顺序违背约束条件就会受到较大的惩罚,因为模型中的目标函数值都是正数,且约束中的正偏移量也均为正数,所以满足约束条件的个体对应的适应度函数值必定是正数,而不可行的个体对应的适应度函数值则为负数。
种群进化过程中不可避免地会出现彼此相同的重复个体或不可行个体,由于重复个体占据过多的种群空间,造成种群空间资源的浪费,不可行个体使得种群存在不合理性,易产生进化方向的倾斜,两者的存在不利于种群的优化,为此,需要不断地对种群进行修复,修复规则如下:
由于本文的问题考虑到机器的检修计划,在排定的批量顺序中确定批量的加工时间时需要避开机器检修的时间。在确定每个批量加工时间时,不仅需要考虑工件的加工时长和调整时间,还要考虑检修计划的时间。下面根据模型中的约束(4)和约束(5),具体分析批量的加工开始时间和结束时间的确定。
对于最终得到的批量加工顺序Z={z1,…,zk},计算其中每个批量的加工开始时间和结束时间的方法如下:
(1)对于加工顺序中处于第一位的批量z1,由于机器处于准备加工的状态,不考虑调整时间,其原则上的加工开始时间为计划开始时间,即bz1=0,进而判断该批量加工过程中是否有检修计划,即是否满足可直接加工条件bz1+pbz1≤min{Sm|bz1≤Sm,m∈M}:
1)若满足可直接加工条件,即加工过程中无检修计划,则可直接得到批量z1的加工完成时间Cbz1=pbz1。
2)若不满足条件,则找出所有跨越的检修计划集合Mz1={m|bz1≤Sm,bz1+pbz1≥Em,m∈M},考虑到加工过程不能跨越检修计划,更新批量z1的实际开始加工时间为bz1←max{Em|m∈Mz1},进而得到完工时间Cbz1=bz1+pbz1。
(2)对于加工顺序中其他位置的批量zi(i=2,…,k),由于机器已经经过一定的加工过程,处于上一个批量zi-1加工完成状态,需要根据批量与上一个加工完成的批量之间的属性相关性关系,判断是否需要进行机器调整,即通过约束(6)计算调整时间szi-1zi。原则上批量zi的开始时间为bzi←Cbzi-1+szi-1zi,进一步判断是否跨越检修计划,该过程与批量z1的相同。
通过上述两个过程,得到批量加工顺序Z={z1,…,zk}中每个批量zi的加工开始时间和完成时间,则目标函数(1)~(3)可以直接通过计算得到。
2.5 非支配排序和拥挤度的计算
非支配排序和拥挤度计算是对种群中的个体进行评估的过程,是NSGA-Ⅱ算法确定个体优劣的基本步骤。为了更好地实现评估过程,首先,针对本文问题的特点,确定解的支配及相关概念[12]:
定义1 支配。原则上若解x=(x1,x2,…,xn)支配解x′=(x′1,x′2,…,x′n),则当且仅当对任意的目标函数fi∈F(F为目标函数集合),满足fi(x)≤fi(x′)且∃fi∈F,使得fi(x)<fi(x′)。
定义2 非支配解。若解x=(x1,x2,…,xn)为非支配解,则当且仅当在当前所有参与对比的解X={x0,x1,…,xk}中,不存在一个xj,使得对任意的fi∈F都满足fi(xj)<fi(x)。
(1)非支配排序
非支配排序主要根据支配概念对种群中的个体进行优劣排序,并确定个体的非支配等级[10]。对于规模为popSize的种群P中的每个个体xi,首先设置种群中支配个体xi的个体数量ni和种群中被个体xi支配的个体集合Subi两个参数。具体的排序过程为:
1)令前沿非支配级别rank=1,针对整个种群,寻找所有的非支配解,即ni=0的个体xi,令其非支配等级rank(xi)=1,并存入第一级前沿非支配集合F1中,同时,Subi也得以确定。
2)令rank←rank+1,对每个个体xi∈Frank-1对应的集合Subi,检验其中的每个个体xj∈Subi的nj,令nj=nj-1,若满足条件nj=0,则令个体xj的非支配级数为rank(xj)=rank,并由所有级数为rank的个体构成第rank级前沿非支配集合Frank。
3)重复步骤2),将种群的个体依次进行分级,直到所有的个体都归入相应的等级集合中。
(2)计算拥挤度
拥挤度描述的是处于同一非支配级的所有个体与其周围其他个体之间的密集程度,NSGA-Ⅱ算法根据个体的拥挤度,淘汰拥挤度较小的个体,保留拥挤度较大的个体,从而保证解的多样性。拥挤度的计算主要是对每个适应度函数,对所有的同级个体按照在该适应度函数下的函数值进行排序,并计算个体与前后个体的拥挤距离,处于序列两端的个体,由于其前(后)没有个体存在,将其拥挤距离设为正无穷大,最后将个体在所有适应度函数条件下得到的拥挤距离相加,得到个体的拥挤度[13]。具体表示如下:
个体xi∈Frank在某个适应度函数fv∈F下的拥挤距离为
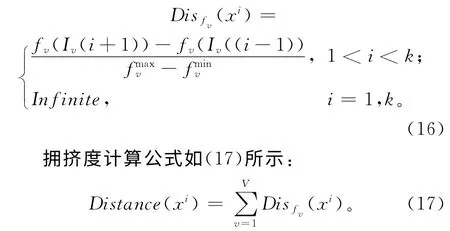
式中:k为Frank中个体的总数量;V为适应度函数的个数;Iv(i-1)和Iv(i+1)分别为按第v个适应度函数对解排序后,位于xi前后的解和分别为所有当前解对应的适应度函数fv的最大值和最小值。
2.6 选择策略
选择策略的目标是使种群进化朝着非劣解和均匀分布的方向进行,选择的主要依据为个体的非支配等级以及拥挤度。
借鉴二元联赛选择机制的思想,首先设置选择容量popSize′并初始化集合P′t=∅,选择规则为:在父代种群Pt中,随机选择两个不同的个体xi,xj:
(1)若rank(xi)>rank(xj),则Pt′←Pt′∪{xj};
(2)若rank(xi)<rank(xj),则Pt′←Pt′∪{xi};
(3)若rank(xi)=rank(xj),则比较两个个体的拥挤度,更 新Pt′←Pt′∪{x′},其中,x′=xi,Distance(xi)>Distance(xj)或x′=xj,Distance(xj)>Distance(xi)。
如此反复地从父代种群Pt中选择成对的个体并作出选择,直到集合Pt′内的个体数量达到pop-Size′,即|Pt′|=popSize'。最终得到的集合Pt′即是下一步进行遗传操作的集合。
2.7 遗传算子
遗传操作是NSGA-Ⅱ实现种群进化的关键步骤,其效果的好坏依赖于交叉和变异两种算子的设计和选择。为了取得较好的问题求解效果,本节将结合问题的求解特征对交叉算子和变异算子进行详细设计。
(1)交叉算子
交叉算子作为个体进化的一种方式,对个体的进化起着主要作用,决定遗传操作的全局搜索能力,是决定算法收敛性能的关键。考虑到算法的编码方式是自然顺序排列的批量号,采用基本的交叉方法可能会导致基因重复或丢失,并且交叉中的基因相对位置的改变对新个体的可行性具有一定的影响。为了达到较好的交叉效果,本文借鉴文献[14]中的线性序号交叉法(Linear Order Crossover,LOX)和C1两种交叉方法。采用概率选择的方式交互使用两种方法,即通过预先设置交叉选择概率pc∈(0,1),比较随机生成的数值rc∈(0,1)与pc的大小,通过比较结果选择两种方法中的一种进行交叉操作。
(2)变异算子
变异算子是种群进化的另一种操作方式,主要用来保持种群多样性。对待变异的个体,本文采用常用的交换方式:随机选择两个位置的基因进行位置互换,形成的新的基因序列构成新的个体。预先设置变异概率pm∈(0,1)和循环整数参数T,对种群中的每个个体,根据随机生成的数值rm∈(0,1)与pm的大小对比结果决定是否变异,对于决定进行变异操作的个体,随机选择基因序列中的两个基因交换位置,并循环T次,得到新个体。
2.8 基于有限搜索范围的邻域搜索
邻域搜索是为了从当前解的邻域中找出更好的解,避免算法陷入局部最优。对于调度问题,通常用于邻域搜索的方法有插入和交换两种,并且插入是比交换更为有效的方法。在算法进行邻域搜索前,首先设置一个搜索决策概率ps∈(0,1),对于种群中的每个个体,通过比较随机数值rs∈(0,1)与ps的大小决定是否进行邻域搜索,若rs<ps,则进行邻域搜索,否则,进入下一步计算。由于个体中某个被选择的基因可选择插入的位置较多,尤其对于基因序列较长的个体,若邻域搜索考虑的是全部的可插入位置,则会产生较长的搜索时间,不利于提高算法的搜索效率。
本文通过改进基本的插入方法,有限制地选择插入位置,即对某个基因,通过设定搜索长度参数α,选择部分位置做插入操作,以减少搜索时间。同时,为了节约计算时间,在进行邻域搜索时,若找到一个比原解更优秀(非支配)的新解,则停止搜索,用新解代替原解。
对待进行邻域搜索的个体x={x1,x2,…,xk},算法及具体操作如下:
算法2 邻域搜索算法。
步骤1 设置搜索长度参数α。
步骤2 令i从1~k变化,选择位置为i的基因xi,将其移出基因序列,确定xi可插入的位置集合S={i-1,i-2,…,max(i-α,1),i+1,i+2,…,min(i+α,k)}。
步骤3 令j从1到min(α,i-1)+max(α,ki)变化,选择插入位置S(j),将xi插入到位置S(j),形成临时解xj。
步骤4 根据式(13)~式(15)计算xj的适应度函数值,并确定与x的支配关系,若x受xj支配,则选择xj替代原解x,x←xj,并停止搜索,执行步骤6,否则,令j←j+1,执行步骤3,若j=min(α,i-1)+max(α,k-i)仍不能更新x,则执行步骤5。
步骤5 令i←i+1,执行步骤2,直到i=k,执行步骤6。
步骤6 输出x,算法结束。
2.9 精英策略
精英策略是在父代种群和子代种群中选择优秀的个体,是算法收敛的条件,其具体方法为:
步骤1 将父代种群Pt与经过选择操作、遗传操作以及邻域搜索后形成的子代种群Qt进行合并,得到混合种群Rt,即Rt=Pt∪Qt,且Size+popSize′。
步骤2 对所有的x∈Rt进行非支配排序确定非支配等级Rank(x)并计算拥挤度Distance(x),根据非支配等级和拥挤度大小排定个体间的优劣顺序。采用的排序规则具体如下:对∀xi,xj∈Rt,其优先级o(xi),o(xj)的大小关系为:
(1)若Rank(xi)<Rank(xj)或Rank(xi)=Rank(xj)∧Distance(xi)>Distance(xj),则o(xi)>o(xj);
(2)若Rank(xi)>Rank(xj)或Rank(xi)=Rank(xj)∧Distance(xi)<Distance(xj),则o(xi)<o(xj)。
步骤3 选择序列的前popSize个个体构成精英集,将精英集作为下一次算法迭代的父代种群Pt+1。
2.10 MNSGA-Ⅱ算法的计算步骤
步骤1 种群初始化。
步骤1.1 令种群进化代数为t=0,种群规模为popSize,最大迭代次数为Iter,子群规模为pop-Size′,交叉选择概率为pc,变异选择概率为pm,变异整数参数为T,邻域搜索决策概率为ps,搜索长度参数为α;
步骤1.2 采用MNEH 算法(算法1)产生初始父代种群Pt={x1,x2,…,xpopSize}。
步骤2 种群修复。
步骤2.1 选择种群Pt中重复的个体,根据重复个体的修复规则(规则1)进行修复。
步骤2.2 采用目标函数计算方法,根据式(13)~式(15)计算种群Pt中每个个体的适应度函数值,并对不可行个体进行修复(规则2)。
步骤3 非支配排序并计算拥挤度。
步骤3.1 非支配排序,对种群Pt的所有个体进行非支配分级,为每个个体赋予非支配等级,等级为i的所有个体构成前沿非支配集合Fi,所有的Fi形成总非支配集F′={F1,F2,…,Fr};
步骤3.2 对每个Fi∈F′,根据式(16)和式(17)计算每个x′∈Fi的拥挤度Distance(x′)。
步骤4 遗传操作。
步骤4.1 根据选择策略选择popSize′个个体构成待进化的临时种群Pt′。
步骤4.2 对Pt′中的个体进行交叉操作,对待交叉的个体x,x′∈Pt′,将随机数值rc∈(0,1)与pc对比,若rc≤pc,则选择交叉方式LOX,否则选择交叉方式C1。
步骤4.3 对Pt′中的个体进行变异操作,对个体x∈Pt′,将随机数值rm∈(0,1)与pm对比,若rm≤pm,则对x进行变异操作,否则,不进行变异操作。
步骤4.4 种群Pt′经过交叉和变异两种遗传操作,进化形成新的子代种群Qt。
步骤5 选择精英集。
步骤5.1 对每个x∈Qt,通过随机产生的数值rs∈(0,1)与ps的对比结果决策是否进行邻域搜索,对需要进行邻域搜索的个体x,采用基于有限搜索范围的邻域搜索算法(算法2)进行邻域搜索,更新子代种群Qt。
步骤5.2 根据精英策略构造新的父代种群Pt+1,并更新Pt←Pt+1。
步骤6 判断终止条件。
步骤6.1 令t=t+1,若t>Iter,则执行步骤6.2,否则返回执行步骤2。
步骤6.2 输出种群Pt中的非支配解,算法结束。
3 数据实验
本文采用Microsoft Visual C#实现算法,实验环境为Pentium4.1/2.90GHz/2.00GB/Windows 7。根据已有数据的多次试验,发现MNSGA-Ⅱ算法参数如下设置在多数情况下具有更好的求解效果:种群大小popSize=200;选择进行遗传操作的子种群大小popSize′=20;交叉选择概率pc=0.6;变异概率pm=0.06;变异整数参数T=10;邻域搜索决策概率ps=0.5,搜索长度参数根据批量数计算得到,记为α=1/5k(k为批量数量);最大迭代次数100,每轮迭代均独立运行10 次,仿真结果取所有迭代的平均值。
本文实验分为两部分:①通过对实际的生产数据进行实验,验证算法解决实际问题的能力;②根据实际生产的数据范围,采用人工方式产生不同规模数据,检验算法的求解质量,为了验证算法的有效性,将其与MNEH 和基本的NSGA-Ⅱ算法进行比较,其中NSGA-Ⅱ算法的初始解通过随机方式产生,其他步骤与MNSGA-Ⅱ相同。
3.1 第一组实验
以国内某特钢企业在某计划期间内的237个订单经过组批后形成的108个轧制批为基本数据源,并将批量信息及生产数据整理成模型参数,包括产品规格、钢种和每个规格对应的机架类型和数量、钢种的优先级,机器检修维护时间以及机器调整的单位时间(其中tu=10min,td=5min,tr=20min)。分别采用MNSGA-Ⅱ算法、NSGA-Ⅱ算法和MNEH 对实例模型进行测试。实验结果如表1和图2所示,其中:表1中的结果数据取每个算法的所有非支配解的平均值,图2给出了两算法迭代100次后得到的20个染色体(非支配解)对应的三种目标函数值对比曲线。
由以上实验结果可以得到以下结论:
(1)由表1可以看出,在对实际问题的求解中,MNSGA-Ⅱ算法在求解质量上优于MNEH 算法,这是由于MNSGA-Ⅱ算法以MNEH 得到的解作为初始值再进一步优化,从而对各个目标函数值均有不同程度的改善;另外,虽然MNSGA-Ⅱ算法在计算时间上略多于MNEH 算法,但计算时间在允许范围内,符合实际需求。

表1 第一组实验——MNEH 与MNSGA-Ⅱ对比结果
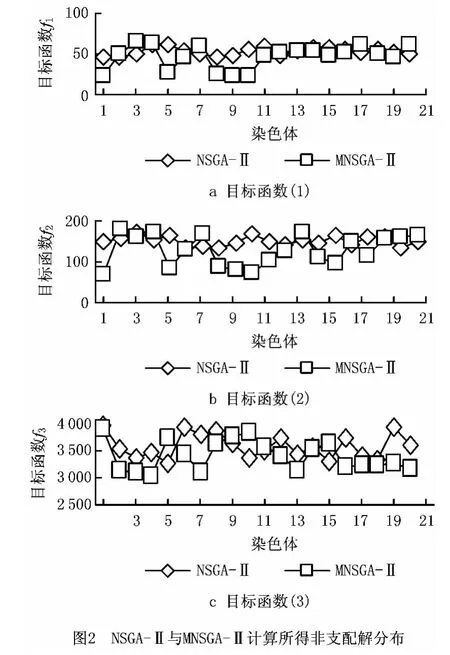
(2)图2 是MNSGA-Ⅱ与NSGA-Ⅱ求得的非支配解对应的目标函数值,从图中可以看出,MNS-GA-Ⅱ算法得到的非支配解质量明显优于NSGA-Ⅱ算法,MNSGA-Ⅱ和NSGA-Ⅱ仅在初始解的构造策略上不同,因此,通过对比可以看出,基于MNEH算法的初始解构造机制对问题的求解能够起到较好的作用。
3.2 第二组实验
该组实验中,根据钢铁企业实际生产的相关数据,通过随机的方式生成批量及订单的各项属性值,包括订货量、交货期、规格和钢种等,其中规格和钢种在企业所能生产的所有种类中随机选择。实验根据不同的批量数量分为5组,每组生成10个算例,对每个算例,其结果数据取每个算法所有非支配解的平均值,最终的计算结果取10个算例的平均值。
实验结果如表2 所示,其中time表示MNSGA-Ⅱ算法的计算时间。
由以上实验结果可以得到以下结论:
(1)针对不同规模的订单量,MNSGA-Ⅱ算法得到的解的质量都优于MNEH 和NSGA-Ⅱ。一方面,MNSGA-Ⅱ是以MNEH 得到的解作为初始解进行优化,并且MNEH 采用随机权重法将多目标化解为单目标进行求解,权重取值的随机性使得MNEH 的解不稳定,MNSGA-Ⅱ能够在此基础上对解进行优化改善,得到更好的解;另一方面,MNEH 产生的初始解要比随机生成的初始解具有更好的目标适应性,因此,MNSGA-Ⅱ能够比NSGA-Ⅱ得到更优秀的解。
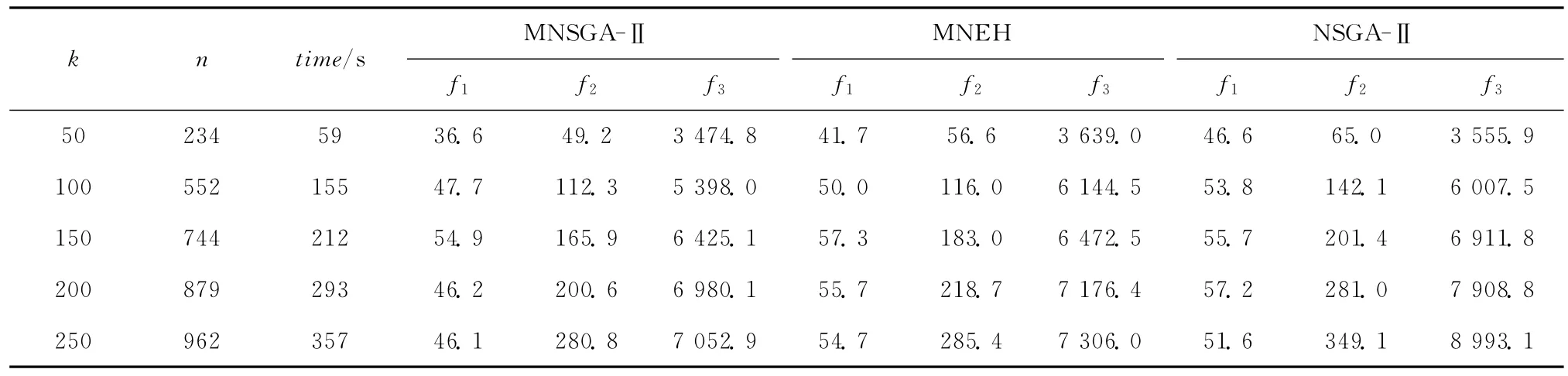
表2 第二组实验计算结果
(2)随着问题规模的不断增大,种群个体的基因序列逐渐增长,MNSGA-Ⅱ算法所用的计算时间也逐渐增加,但对于订单规模为250的问题,算法也能在6min内得到较满意的解,能够满足批量调度的实际应用需求。
4 结束语
热轧批量调度是钢铁企业生产管理中的关键问题,在理论和实践中具有重要的研究意义,本文针对圆钢的热轧批量调度问题,考虑机器检修计划的约束,将问题归结为带有多种约束条件的具有顺序依赖调整时间的flowshop调度问题,并在此基础上建立了多目标的整数规划模型。通过分析问题的求解特点,提出了MNSGA-Ⅱ算法。首先,采用MNEH算法生成初始解,利用罚函数的思想设计适应度函数并对重复个体和不可行个体进行淘汰或修复;其次,在基本的NSGA-Ⅱ的基础上,结合问题的特点,设计了遗传操作方式以及基于有限搜索范围的邻域搜索算法,使得算法朝着最优的方向进化的同时避免陷入局部最优。仿真实验表明,MNSGA-Ⅱ算法对圆钢热轧批量调度问题具有较好的求解效果,且计算效率满足实际应用的需求。
[1]LI Tieke,GUO Dongfen.Model and algorithm for hot-rolling batch plan on constraint satisfaction[J].Control and Decision,2007,22(4):389-393(in Chinese).[李铁克,郭冬芬.基于约束满足的热轧批量计划模型与算法[J].控制与决策,2007,22(4):389-393.]
[2]ZHANG Wenxue,LI Tieke.Batch plan optimization of steel integrated production with multiple process[J].Computer Integrated Manufacturing Systems,2013,19(6):1296-1303(in Chinese).[张文学,李铁克.面向多种生产工艺的冶铸轧一体化批量计划优化[J].计算机集成制造系统,2013,19(6):1296-1303.]
[3]PAN C C,YANG G K.A method of solving a large scale rolling batch scheduling problem in steel production using a variant of column generation[J].Computers &Industrial Engineering,2009,56(1):165-178.
[4]JIA S J,YI J,YANG G K,et al.A multi-objective optimization algorithm for the hot rolling batch scheduling problem[J].International Journal of Production Research,2013,51(3):667-681.
[5]TANG L X,HUANG L.Optimal and near-optimal algorithmsto rolling batch scheduling for seamless steel tube production[J].International Journal of Production Economics,2007,105(2):357-371.
[6]LI Lin,HOU Jiazhen.Multi-objective flexible job-shop scheduling problem in steel tubes production[J].Systems Engineering—Theory &Practice,2009,29(8):117-126(in Chinese).[李 琳,霍佳震.钢管生产计划中的多目标柔性Job-shop调度问题[J].系统工程理论与实践,2009,29(8):117-126.]
[7]SHI C T,YANG G J,LI T K.An evolutionary neighborhood search algorithm for flexible job-shop scheduling problem in steel tube production[J].Advanced Materials Research,2012,566:620-627.
[8]ASAD R,DEMIRLI K.Production scheduling in steel rolling mills with demand substitution:Rolling horizon implementation and approximations[J].International Journal of Production Economics,2010,126(2):361-369.
[9]WANG Xin,YANG Chunhua,QIN Bin.Multi-objective hybrid optimization of lot scheduling for bar mill process[J].Control and Decision,2006,21(9):996-1000(in Chinese).[王 欣,杨春华,秦 斌.棒线材轧制批量调度多目标混合优化[J].控制与决策,2006,21(9):996-1000.]
[10]DEB K,PRATAP A,AGARWAL S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation,2002,6(2):180-197.
[11]ISHIBUCHI H,MURATA T.A multi-objective genetic local search algorithm and its application to flowshopscheduling[J].IEEE Transactions on System,Man,Cybernetics,1998,28(3):392-403.
[12]LI Qian,GONG Jun,TANG Jiafu.Multi-objective optimal cross-training plan models using non-dominated sorting genetic algorithm-Ⅱ[J].Journal of Northeastern University:Natural Science,2011,32(12):1696-1699(in Chinese).[李倩,宫 俊,唐加福.基于改进NSGA-Ⅱ的交叉培训规划多目标优化[J].东北大学学报:自然科学版,2011,32(12):1696-1699.]
[13]WEI Tian,FAN Wenhui.Modified NSGAⅡalgorithm for vehicle routing problem in logistics[J].Computer Integrated Manufacturing Systems,2008,14(4):778-784(in Chinese).[卫 田,范文慧.基于NSGAⅡ的物流配送中车辆路径问题研究[J].计算机集成制造系统,2008,14(4):778-784.]
[14]WANG L,ZHANG L,ZHENG D Z.An effective hybrid genetic algorithm for flow shop scheduling with limited buffers[J].Computers &Operations Research,2006,33(10):2960-2971.
