不同再调度周期下的柔性作业车间动态调度

汪双喜，张超勇+，刘 琼，饶运清，尹 勇

（1.华中科技大学 机械学院数字制造装备与技术国家重点实验室，湖北 武汉 430074；2.武汉理工大学 湖北省数字制造重点实验室，湖北 武汉 430074）

0 引言

柔性作业车间调度问题（Flexible Job-shop Scheduling Problem，FJSP）是经典作业车间调度问题（Job shop Scheduling Problem，JSP）的扩展，它不但考虑机器上待加工工序的加工顺序，而且考虑各个工序是由哪台机器进行加工，更符合实际生产的需要。然而，FJSP 减少了机器约束，扩大了可行解的搜索范围，增加了问题的求解难度，是比JSP更为复杂的NP-hard问题。鉴于此，人们将研究目标转向各种启发式方法。在众多的研究与探索中，通过模拟自然界中生物和人类行为过程中所表现出的某些特点而发展的群体智能算法，如遗传算法、粒子群优化算法、蚁群优化算法、差分进化（Differential Evolution，DE）算法等，在包括调度问题在内的组合优化问题求解领域中，受到越来越普遍的关注。近年来，大量学者对FJSP 进行了研究，Bagheri等［1］使用人工免疫算法求解FJSP，Wang 等［2-3］分别使用人工蜂群算法和分布估计算法求解FJSP，在求解过程中平衡了局部搜索和全局搜索过程。其中DE算法由Storn和Price［4］于1997年提出，是最新的基于种群的进化算法之一，其最初的设想是用于解决连续性问题。由于DE 算法具有思路简单、容易实现、收敛速度快和稳定性好等优点，近年来被广泛应用于解决复杂优化问题，如人工神经元网络、化工、电气和经济学等，但对于调度问题这种典型的离散型问题研究得还不多，尤其对于FJSP 问题，少有学者用DE算法进行研究。

实际环境下的FJSP 不但具有计算复杂性，而且有多目标和动态性特征，具体表现为：①生产过程是动态的，各个工件依次进入待加工状态，进入系统接受加工，同时完成加工的工件又不断离开过程；②调度优化决策不仅包括时间、成本等静态指标，还包括鲁棒性和稳定性等动态指标，各个指标之间通常互相冲突和耦合，需要对多个目标同时进行优化与决策。多目标和动态性是当今制造系统必须解决的一个关键问题，经典调度的研究忽略了生产需求的动态性和生产过程的健壮性与稳定性，造成了理论研究距离实际应用有相当的差距。

Nelson等［5］在1977年最早提出了动态调度问题，它将动态调度过程分成多个连续的静态区间，然后对上述调度区间进行优化以达到每个区间内最优，从而适应动态环境；张超勇研究了原材料延期到达、加工时间延误、紧急工件加入等情况下的动态调度；潘全科等［6］研究了待加工工件的选取原则和再调度周期的确定方法；Branke等［7］研究了工件随机到达的动态调度，以合并早期空闲时间的方法来提高调度效率；Chryssolouris等［8］用遗传算法对动态作业车间调度问题（Dynamic Job-shop Scheduling Problem，DJSP）进行了求解，并考虑了两个目标，进而说明多目标调度在动态调度中的可行性；Rangsaritrasamee等9提出了一种同时考虑效率与稳定性的多目标优化策略，其采用加权的方式将两目标合成为单目标问题进行研究；刘爱军等［10］提出一种自适应遗传算法的多目标柔性动态调度算法，基于事件和周期驱动的混合再调度策略来求解实际的调度问题。

群体智能算法可以在一次运行中得到多个Pareto解，非常适合求解多目标优化问题。国内外学者目前在这方面做了大量研究，提出了多种多目标进化算法（Multi-Objective Evolutionary Algorithm，MOGA），如非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm，NSGA-Ⅱ）等，其中多目标差分进化有较好的收敛性和分布性，越来越受到国内外学者的关注。本文运用概率方法模拟各个工件的到达时间，采用周期性再调度的调度策略将各工件划分到对应的调度区间进行求解。在每个调度区间上，以稳定性和效率为优化目标，设计基于Pareto解的多目标差分进化算法进行求解，并研究不同的再调度周期对调度性能的影响，从而有效地指导生产。

1 动态调度问题描述与转化

为了研究不同再调度周期对调度性能的影响，本文采用概率方法模拟了各工件的到达时间，并针对这些先后到达的工件进行动态调度。动态调度采用周期性再调度策略，将各工件依其到达的时间划入相应的调度区间中，进而在各调度区间进行多目标优化。

1.1 工件到达时间模拟

许多研究显示：在一定时间，内车间中工件随机到达的个数服从泊松分布，设泊松分布的参数为λ，表示工件的平均到达率，则任意两个先后到达的工件之间的时间间隔服从参数为λ的指数分布。Karisiti等［11］在研究作业车间调度问题时提出一个关于到达率的计算公式，

式中：λ表示工件的平均到达率；U表示车间利用率（shop utilization）；m表示车间的机器数量；μp表示工序的平均加工时间；μg表示每个工件的平均工序数。

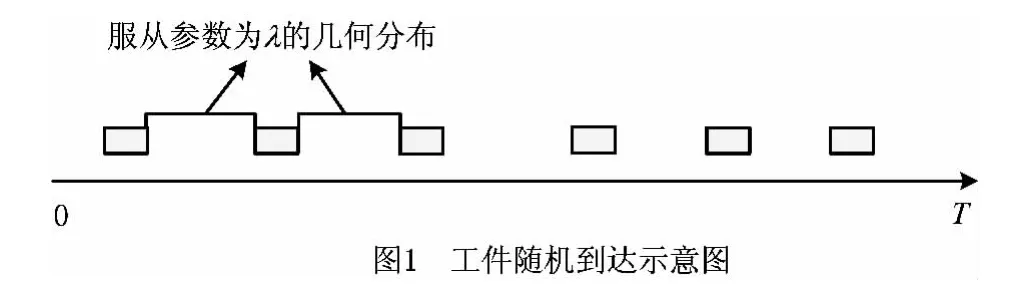
工件随机到达的示意图如图1所示，任意两个先后到达的工件之间的时间差服从参数为λ的几何分布。通过模拟一组服从几何分布的随机数列，将数列中的各值依次作为先后到达的两个工件的到达时间差，然后累计得到各个工件的实际到达时间。设工件Ji的到达时间为ai，数列b1，b2，…，bn为模拟得到的服从几何分布的数列，t0为模拟的第一个工件J1的到达时间，即a1=t0，则工件Jn的到达时间an可由式（2）得到：

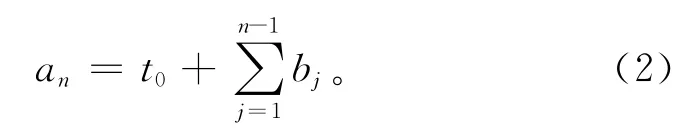
为了方便研究，本文设第一个工件的到达时间t0=0。

1.2 动态调度策略与调度区间划分

对于动态调度问题，通常采用周期和事件驱动再调度的调度策略。本文主要探讨不同再调度周期对调度性能的影响，进而采用周期性再调度的调度策略。在不同的再调度周期下对先后到达的相同数量的工件进行调度，并对最后的性能指标进行比较和分析。

在周期性再调度模型中，将每一次进行再调度的时间称为再调度时刻，每进行一次再调度即产生一个调度区间，该调度区间的长度为上一次再调度时刻与当前再调度时刻之间的长度（在再调度周期ΔT不变时即为一个再调度周期的时间长度）。每个调度区间上需要进行调度的工件包括：①在上一个调度区间中进行了调度但在当前再调度时刻还未加工完成的工件；②在上一个再调度时刻与当前再调度时刻期间到达的新工件。通过这种策略对先后到达的工件进行动态调度时，可以将各个工件依其到达时间划分到对应的调度区间中，进而将动态调度转化为多个连续的调度区间上的静态调度问题进行求解。工件所属的调度区间为

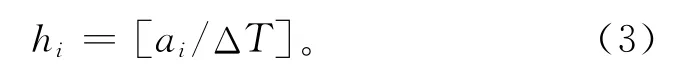
式中：hi表示工件Ji初次进行调度所属的调度区间；ai表示工件Ji的到达时间；ΔT表示再调度的调度周期。因为工件J1在0时刻到达，而它应在第一个调度区间进行调度，所以修改得h1=1。

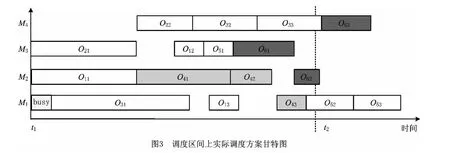
周期性再调度策略以及调度区间的产生过程如图2所示。在图2的示例中，ΔT为再调度的周期，t1，t2和t3为三个连续的再调度时刻，其中t2=t1+ΔT，t3=t2+ΔT。调度区间A和调度区间B为两个相邻的调度区间。调度区间B是在t2再调度时刻产生的，该调度区间中需要进行调度的工件包括调度区间A在当前再调度时刻t2还没有加工完成的工件（去除当前正在加工的工序以后还有未加工工序）和在上一个再调度时刻t1与当前再调度时刻t2之间新到达的工件。调度区间B中各机器的加工状态需要根据调度区间A上的实际调度方案确定。设调度区间A上的实际调度方案甘特图如图3所示，则调度区间B上的各机器状态可按如下方法确定：

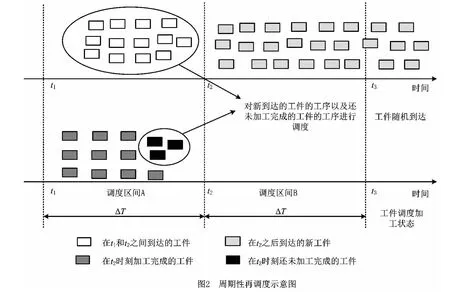
在图3 中，依据调度区间A上的最终调度方案，在再调度时刻t2到达时，工序O33，O52和O62正在进行加工，工序O53和O63还未开始加工，即工件J5和J6在t2时刻还未加工完成，因此要并入下一个调度区间B进行再调度。机器M1，M2和M4正在在加工工序O52，O62和O33，则在调度区间B中，对应的机器只能加工完成上述工序后才能开始加工调度区间B中的工件，在t2时刻处于“忙碌”状态，而机器M3在t2时刻空闲。调度区间B是再调度时刻t2产生的，该调度区间上各机器的最早可用时间为t2（如机器M3，在t2时刻空闲）或为当前正在加工工序的完工时间（如机器M1，M2和M4）。

本文研究了不同再调度周期对相同数量工件进行调度时的性能指标差异。在本文的研究实例中，第一个工件J1的到达时刻a1=0，即在0时刻只有一个工件，为了方便研究，并保证各机器不论调度区间ΔT为多少，第一个调度区间均在当前调度时刻可用，令第一个再调度时刻为ΔT而不是0 时刻。第一个调度区间上的工件包括从0时刻～ΔT时刻到达的新工件，该调度区间中各机器均在ΔT时刻可用，各机器的最早可加工时间均为ΔT。以后每隔ΔT的时刻进行再调度，产生新的调度区间，直到所有的工件都被调度加工完成为止。

按照上述再调度策略和调度区间的划分方法，可以将动态调度问题转化为连续的调度区间上的静态调度问题。在每个调度区间上，根据上一个调度区间的实际调度方案得到各机器在当前再调度时刻的可用状态，合并该调度区间上新到达的工件和需要再调度的工件得到所有待调度工件集合，进而对该调度区间上的调度问题采用优化算法进行求解。

2 调度区间上的多目标调度

2.1 调度区间上的问题描述

调度区间上的调度问题相当于一个静态的FJSP，为了区别调度区间上的第i个工件和按照模拟得到的到达时间第i个到达的工件，用Ji′表示前者，Ji表示后者。进而调度区间上的调度问题描述如下：该调度区间上有n′个工件需要进行调度，对应的待加工集合为J′=｛J1，J2，…，Jn′｝；共有m台机器加工这些工件，对应的机器集合为M=｛M1，M2，…，Mm｝；工件Ji′由ni′道工序构成，各工序按照次序Oi′，1，Oi′，2，…，Oi′，ni′依次加工；工件Ji′的第j道工序Oi′，j可以被其可加工机器集合Mi′，j中的任意机器加工，其中Mi′，j⊆M；工序Oi′，j的加工时间因其加工机器不同而各不相同。为了使研究更具可操作性，本文设定以下假设条件：

（1）各机器在当前再调度时刻的可用状态由上一个调度区间的实际调度方案确定。

（2）该调度区间所有新到达的调度工件均在当前再调度时刻可被加工。

（3）该调度区间上所有需要进行再调度的工件，可被加工的最早时间为当前再调度时刻与该工件已经被加工的最后一道工序的完工时间中的较大值。

（4）一台机器一次只能加工一道工序。

（5）同一工件的同一道工序在同一时刻只能被一台机器加工。

（6）每个工件的每道工序一旦开始加工就不能中断。

（7）不同工件的工序之间没有先后约束，同一工件的工序之间有先后约束。

（8）忽略各机器设备的启动时间和各工序的运输时间。

2.2 优化指标

与传统的静态调度不同，动态调度不仅需要考虑调度效率（Efficiency）指标，还要考虑一个重要的指标——调度的稳定性（Stability），即再调度偏离初始调度的程度。Rangsaritratsamee等［9］最早在作业车间动态调度问题中同时考虑了这两个指标，Fattahi等［12］将前者提出的两个目标进行了扩展，引入柔性作业车间动态调度问题中，但是两者对待双目标问题都是采用加权将双目标问题转化为一个合成的单目标问题进行优化。

本文将上述两个目标引入柔性作业车间动态调度问题中，并在模拟求解过程中采用基于Pareto解的多目标算法进行优化，最后再通过Pareto解决策出每个调度区间中的最优调度方案，作为对应调度区间上的实际调度方案。

2.3 优化算法

DE算法是一种群体进化搜索算法，具有思路简单、容易实现、收敛速度快和稳定性好等优点。它具有记忆个体最优解和种群内信息共享的特点，即通过种群内个体间的合作与竞争实现对优化问题的求解。

Yuan Yuan等［13］在研究FJSP 时，提 出一种 基于实数的编码与解码方法，采用DE 算法进行了求解，并对求解性能与结果进行了比较和分析。结果显示，算法收敛性较好，求解结果也比较理想。考虑到DE算法的优点，本文采用原作者提出的编码解码方案，并同样采用DE算法进行求解。

原作者采用的DE算法仅对完工时间该单目标进行了优化，单目标DE 算法中的变异算子不适用于本文的多目标优化问题。同样在用差分进化算法进行单目标优化时，新种群通过选择操作产生，同样不适用于多目标优化问题。本文针对上述两个操作进行了相应改进，设计了多目标变异算子和新种群的产生策略。

在调度区间上采用基于Pareto解的多目标优化策略，最后得到一个非支配解集D。在本课题的研究中，必须从D中进行Pareto解决策，选出一个调度方案作为该调度区间的实际调度方案，并以此判定哪些工件需要在下一个调度区间进行再调度，以及各机器在下个调度区间再调度时刻的可用状态。

2.3.1 多目标变异操作

对于多目标DE 算法，采用基于Pareto解的方法时，在每一代种群中会得到一个非支配解集DG（non-dominated solutions），G=0，1，…，Gmax，其中G表示种群的代数；同时也可以得到一个进化到当前代数为止的一个全局的非支配解集D。本文针对Xue Feng等［14］提出的多目标变异算子进行相应改进，使得变异操作能够充分利用到全局的非支配解集D，得到式（4）所示的变异操作：

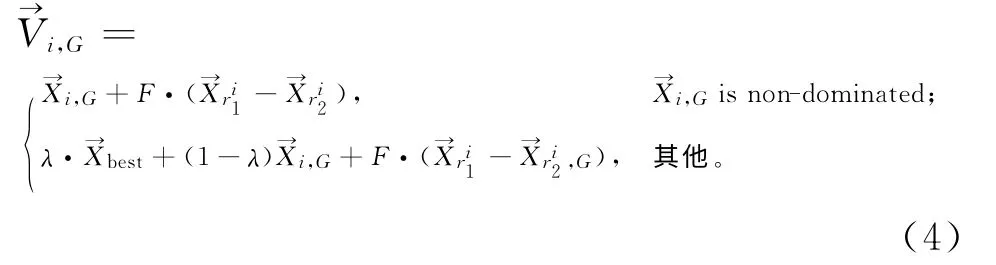
在Xue Feng等［14］提出的算子中，是否被支配以及都是基于当前父代种群中的非支配解集DG考虑的。本文采用全局的非支配解集D进行操作，如果，则说明不能被支配，否则从全局的非支配解集D中随机选择一个作为进行对应操作。

在测试中发现，当前种群的非支配解集DG中的个体往往能被全局的非支配解集D支配。因此用D替换DG进行变异操作可以在一定程度上提高解的质量，也加大找到新的全局非支配集的机会。和是不同于的两个不同的向量，两者之差表示差分向量，F为缩放因子，λ∈［0，1］表示的是贪婪因子。λ越靠近1，差分基向量中所占的比重就越大；λ越靠近0，在差分基向量中所占的所比重就越大。

如果在当前调度区间不存在需要再调度的工件，即待调度工件全是新到达的工件，如第一个调度区间，则该调度区间上将不存在稳定性指标的优化，公式中的变异算子将退化（如式（5）），与Yuan Yuan等［13］采用的单目标变异算子保持一致。

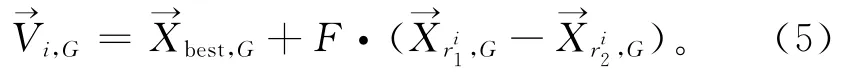
2.3.2 新种群产生策略

父代种群Pt（t表示种群的代数）中的每个个体经过变异、交叉操作后得规模大小同样为Np（Np表示种群规模）的试验向量集合。集合中的每一个试验向量都表示一个可行的调度方案。此时将所有的试验向量并入大小为Np的试验种群Qt，然后将群体Pt和Qt合并到Rt中，针对Rt构造边界集，根据需要计算某个边界集中所有个体的聚集距离，并建立偏序集；然后从偏序集依次选取个体进入Pt+1，直至Pt+1的规模为Np，这样得到的Pt+1即为下一代种群。

2.3.3 Pareto解决策

在调度区间中，采用基于Pareto解的优化算法进行调度后最终会得到一个Pareto非支配解集，而进行加工时只能有一个可行的调度方案，因此必须要从当前的非支配集合中选择出一个满意的调度方案，并以此调度方案作为下个调度区间的基准。在进行Pareto解决策时，本文采用文献［9］的推荐比例，效率（Efficiency）和稳定性（Stability）权重分析设为5和1，依据式（6）计算结果选择满意解，实际操作中可以根据具体情况设定其他合适的决策方案。

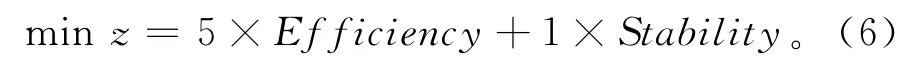
3 实例设置

3.1 工件的加工时间模拟

在柔性作业车间中，各个工序可以在多台机器上加工，且加工时间相互独立。由于可选机器集中的机器加工速率不同等因素，完成同一工序所需要的加工时间也不同。在本文的测试实例中，设工序Oi，j在各机器 上的加 工时间Pi，j，k服从均 匀分布，Pi，j，k～U（0，9）。Pi，j，k=0说明工序Pi，j不能在机器Mk上加工。

3.2 工件到达时间仿真

根据式（1）所示的工件的平均到达率，本文设定实例的相关参数为：加工机器数量m=10，车间利用率U=0.9，每个工件包含15 道工序，即μg=15。平均加工时间μp是一个与加工车间的实际情况相关的经验值，其值往往小于本文设定的对应工序的可加工机器上的加工平均时间5（本文采用的是0～9的均匀分布，期望值为5，由于0表示不能加工，实际可加工时间为1～9）。在本文设定的调度环境中，测试得到当m=10和μg=15时，μp=1.76，其值小于5是因为在实际调度中，各个工件的每道工序通常是在其加工时间比较短的机器上加工。为了方便本课题的研究，使工件的到达更频繁，本文测试实例在μp原值的基础上乘以一个系数，设定μp=1.76×0.7。

3.3 工件交货期模拟

本文采用的效率目标由调度区间上的完工时间和拖期共同确定，为了计算各工件的拖期值，必须要针对其交货期进行设置。很多学者就工件交货期的设定进行了研究，其中Baker等［15］提出的TWK（total work content）规则得到了很多学者的引用。本文针对柔性作业车间调度环境的特殊性，将此模型进行了相应的修改，得到

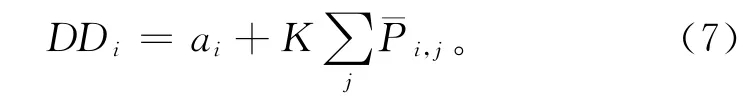
式中：DDi表示工件Ji的交货期；ai表示工 件Ji的到达时间表示工件Ji的第j道工序Oi，j在各个可加工机器上加工时间的均值；K表示松紧因子，在Blocher等［16］给出的推荐值中，该值最小取2，本文取K=2。

4 实验结果与分析

4.1 算法参数设置

在各个调度区间上，本文采用Yuan Yuan等［13］针对FJSP提出的实数编码方案，采用DE 算法进行求解，并针对多目标优化问题就变异算子以及新种群的产生策略进行调整，另外增加了Pareto解决策的操作，但总体上依然采用DE 算法的框架，算法对应的参数也沿袭了Yuan Yuan等［13］测试得出的较好参数，其中包括：缩放因子F=0.1，交叉概率Cr=0.3。对于多目标变异因子中的贪婪因子λ，本文经测试取λ=0.5。另外，在每个调度区间上都要对该调度区间上的待调度工件进行调度优化，而每个调度区间上的待调度工件数均不相同，为了测试方便，文中各个调度区间的种群规模和进化代数都设置为相同值，其中：种群规模Np=500，最大进化代数Gmax=200。

4.2 测试结果与分析

本文在m=10，U=0.9，μg=15，μp=1.76×0.7情况下，对先后到达的500个工件在调度周期ΔT分别为100，200，300，400和500的情况下进行调度加工模拟，分别得到不同调度周期下的总完工时间（500个工件全部加工完成的完工时间）、总拖期（500个工件的拖期值求和）、总效率（由每个调度区间中选择的调度方案对应的效率值求和得到）以及总稳定性（由各个调度区间的稳定性值求和得到）的结果，具体数据如表1所示。

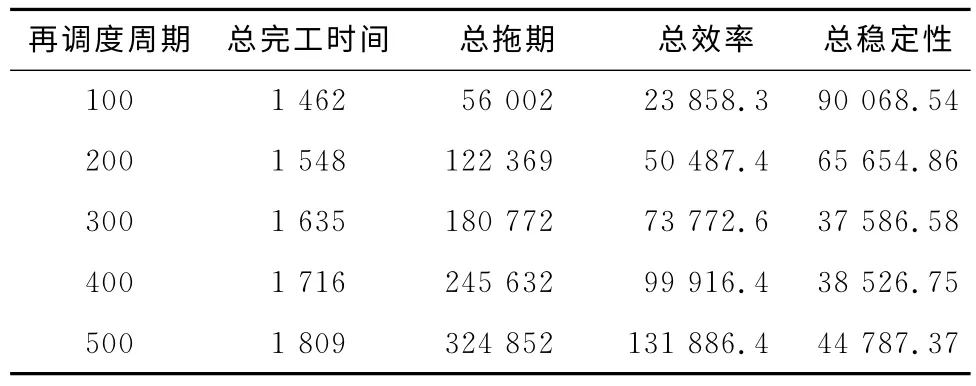
表1 不同再调度周期ΔT 下对500个先后到达的工件进行动态调度得到的各项指标

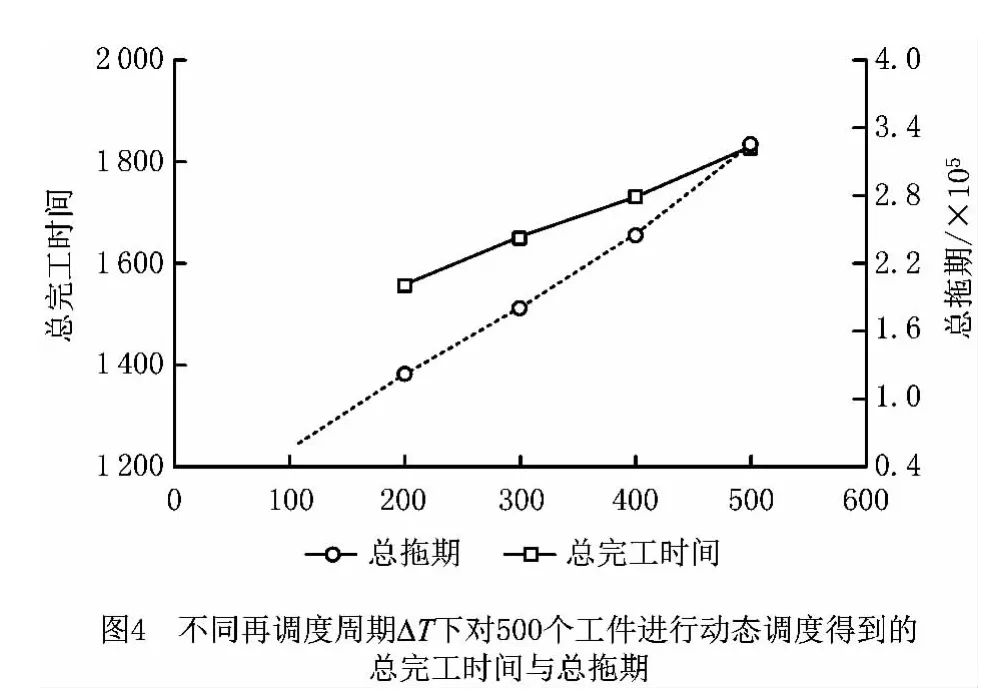
4.2.1 再调度周期ΔT对总完工时间和总拖期的影响

不同再调度周期ΔT下的总完工时间和总拖期如图4所示。从图4中可以看出，随着再调度周期ΔT的增加，总完工时间相应增加，再调度周期ΔT每增加100个时间单位，总完工时间大约增加5%～6%，而总拖期大约增加100%。可见再调度周期ΔT的增加对最后的总完工时间的影响相对较小，但对总拖期有较大影响。增大再调度周期ΔT，则在ΔT的时间内会有更多的新工件到达，从而增加了每个调度区间上的待调度工件总数，也增加了各工件从到达到进行调度的等待时间，进而增大了相应的总拖期。

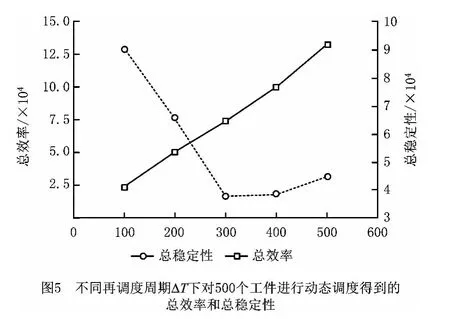
4.2.2 再调度周期ΔT对总效率和总稳定性的影响

不同的再调度周期ΔT对总效率和总稳定性的影响如图5所示。由于效率目标（efficiency）由各个调度区间中的完工时间和拖期加权得到，随着再调度周期ΔT的增加，对拖期的影响非常显著，进而对总效率的影响也非常显著。对于总稳定性，在再调度周期ΔT从100逐渐增加到300的过程中，总稳定性值逐次降低，且降幅比较明显；但再调度周期ΔT从300 增加到400的过程中，总稳定性的变化非常微小，在再调度周期ΔT为300时总稳定性的基础上增加大约2%；再调度周期ΔT从400增加到500时，总稳定性比再调度周期ΔT为400 时有稍大的增加，增幅大约为16%。

4.2.3 再调度周期ΔT对调度区间的影响

由于每个调度区间的长度等于再调度周期ΔT的长度，当对同样数目的先后到达工序进行动态调度时，不同的再调度周期ΔT下需要进行调度的次数不同，每个调度区间上的工件构成也不同。对500个先后到达的工件进行动态调度，再调度周期ΔT=200 的各调度区间上的工件构成情况如表2所示，ΔT=300时再调度周期如表3所示。经简单计算可以得到不同的再调度周期ΔT下，对500个先后到达的工件进行调度加工，调度区间在下一个再调度时刻到达时加工完成的平均工序数，具体如图6所示。从图6中可以看出，每个调度区间内加工完成的工序数和再调度周期ΔT呈正相关。再调度周期ΔT增加，调度区间内的待调度工序数增加，同时调度区间中能够在下次在调度时刻到达时加工完成的工序数也相应增加。

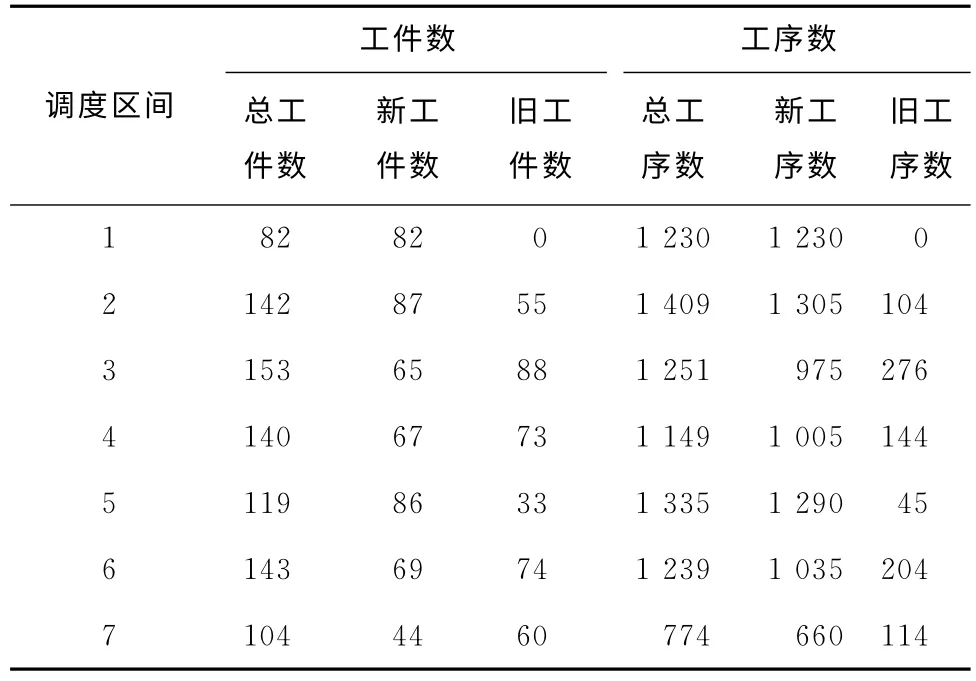
表2 再调度周期ΔT＝200时各调度区间上的工件工序构成

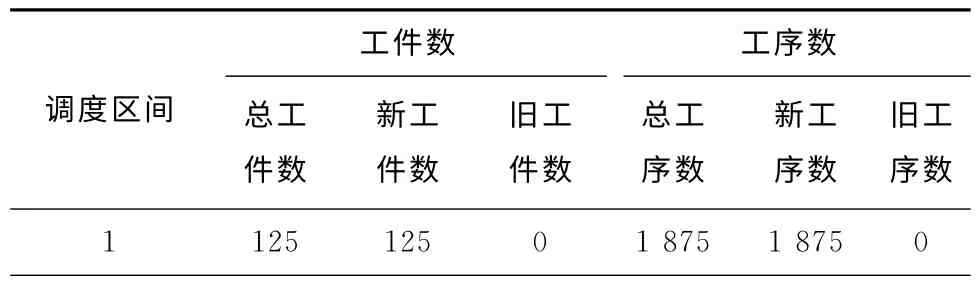
表3 再调度周期ΔT＝300时各调度区间上的工件工序构成

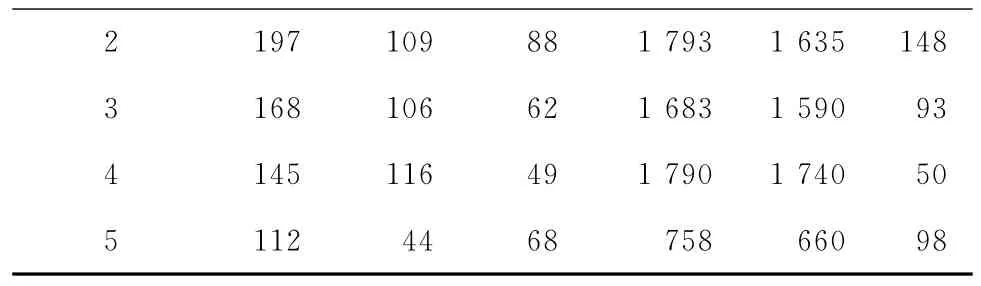
续表3

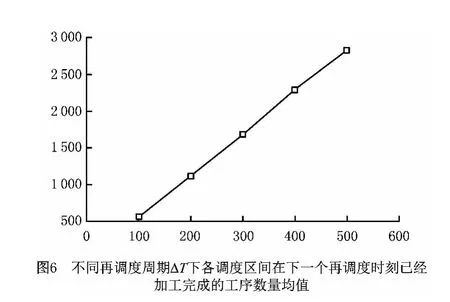
通过在不同再调度周期ΔT下，分析同样数量的先后到达的工件进行调度加工需要进行的调度次数以及各调度区间上的工件工序构成，可以得到总稳定性值随着再调度周期ΔT的增加先减小后增大的原因。对先后到达的同样数量的工件进行动态调度，再调度周期ΔT增加，再调度的次数会相应减少，即对应的调度区间数量会减小，从而使总的稳定性相应减少，因为只有再调度才会产生稳定性值的增加。但是当再调度周期ΔT取值过大时，调度区间中属于再调度类型的工序数增多，两次再调度区间之间的时间间隔（等于）变大，使得需要再调度的工序经常被安排在下一个，甚至下下一个调度区间中才能加工，从而增大了每个被再调度的工序所产生的稳定性值，也相应地提高了总的稳定性。

5 结束语

本文采用概率的方法模拟了各个工件的到达时间，并针对这些先后到达的工件，采用周期性再调度的调度策略进行调度加工，将动态调度问题转化为多个连续的调度区间上的静态调度问题进行求解。在每个调度区间上，采用基于多目标DE 算法，以效率和稳定性为优化目标进行调度优化。采用该方法对先后到达的500个工件在不同的再调度周期ΔT下进行调度加工，并对最后得到的总完工时间、总拖期、总效率和总稳定性进行了分析与比较，得到以下结论：

（1）再调度周期ΔT增大，总完工时间依次增大，但增幅较小，总拖期和总效率依次增大，且增幅较大。考虑到本文的效率指标是通过完工时间和拖期加权得到的，而拖期的变化随着调度周期的变化非常明显，调度周期越长，总拖期越大，总完工时间的变化相对较小。因此在实际生产中当拖期指标很重要时，通常应当减小再调度周期。

（2）再调度周期ΔT逐渐增大时，总稳定性依次减小（稳定性越好），且降幅明显；但当再调度周期ΔT太大时，总稳定性反而增大（稳定性变差）。在实际生产中，应当根据实际的调度加工环境适当设置再调度周期，以满足对稳定性指标的要求。

（3）在实际生产中，效率和稳定性通常会表现出一定的矛盾，即不存在使两个都变优的方案。因此，应当根据实际需要以及对应优化目标的重要程度进行特定优化，以确定最合适的再调度周期ΔT。

柔性作业车间动态调度是生产调度中一个复杂的研究方向，比较符合制造车间中的实际情况，对其开展进一步深入研究显得十分必要，项目组在本文研究的基础上，将在未来开展以下工作：

（1）研究不同调度周期下在每个调度区间中已完成加工的工序数与未开始加工（即需要再调度的工序）的工序数之间的比例关系，并在采用算法求解时针对这一数据进行相应优化。

（2）研究考虑机器故障等动态事件下的柔性作业车间动态调度问题。

［1］BAGHERI A，ZANDIEH M，MAHDAVI I，et al.An artificial immune algorithm for the flexible job-shop scheduling problem［J］.Future Generation Computer Systems，2010，26（4）：533-541.

［2］WANG L，ZHOU G，XU Y，et al.An effective artificial bee colony algorithm for the flexible job-shop scheduling problem［J］.The International Journal of Advanced Manufacturing Technology，2012，60（1-4）：303-315.

［3］WANG L，WANG S，XU Y，et al.A bi-population based estimation of distribution algorithm for the flexible job-shop scheduling problem［J］.Computers &Industrial Engineering，2012，62（4）：917-926.

［4］STORN R，PRICE K.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces［J］.Journal of Global Optimization，1997，11（4）：341-359.

［5］HOLLOWAY C A，NELSON R T.Job shop scheduling with due dates and variable processing times［J］.Management Science，1974，20（9）：1264-1275.

［6］PAN Quanke，ZHU Jianying.Rolling time horizon Job Shop scheduling strategy in dynamic environment［J］.Journal of Nanjing University of Aeronautics &Astronautics，2005，37（2）：262-268（in Chinese）.［潘全科，朱剑英.作业车间动态调度研究［J］.南京航空航天大学学报，2005，37（2）：262-268.］

［7］BRANKE J，MATTFELD D C.Anticipation and flexibility in dynamic scheduling［J］.International Journal of Production Research，2005，43（15）：3103-3129.

［8］CHRYSSOLOURIS G，SUBRAMANIAM V.Dynamic scheduling of manufacturing job shops using genetic algorithms［J］.Journal of Intelligent Manufacturing，2001，12（3）：281-293.

［9］RANGSARITRATSAMEE R，FERRELL J R W G，KURZ M B.Dynamic rescheduling that simultaneously considers efficiency and stability［J］.Computers &Industrial Engineering，2004，46（1）：1-15.

［10］LIU Aijun，YANG Yu，XING Qingsong，et al.Dynamic scheduling on multi-objective flexible Job Shop［J］.Compyter Integrated Manufacturing Systems，2011，17（12）：2629-2637（in Chinese）.［刘爱军，杨 育，邢青松，等.柔性作业车间多目标动态调度［J］.计算机集成制造系统，2011，17（12）：2629-2637.］

［11］KARSITI M N，CRUZ JR J B，MULLINGAN J R J.Simulation studies of multilevel dynamic job shop scheduling using heuristic dispatching rules［J］.Journal of Manufacturing Systems，1992，11（5）：346-358.

［12］FATTAHI P，SAIDI MEHRABAD M，JOLAI F.Mathematical modeling and heuristic approaches to flexible job shop scheduling problems［J］.Journal of Intelligent Manufacturing，2007，18（3）：331-342.

［13］YUAN Y，XU H.Flexible job shop scheduling using hybrid differential evolution algorithms［J］.Computers &Industrial Engineering，2013，65（2）：246-260.

［14］XUE F，SANDERSON A C，GRAVES R J.Pareto-based multi-objective differential evolution［C］／／Proceedings of the 2003Congress on Evolutionary Computation.Washington，D.C.，USA：IEEE，2003：862-869.

［15］BAKER K R.Sequencing rules and due-date assignments in a job shop［J］.Management Science，1984，30（9）：1093-1104.

［16］BLOCHER J D，CHHAJED D，LEUNG M.Customer order scheduling in a general job shop eEnvironment［J］.Decision Sciences，1998，29（4）：951-981.