基于模糊物理规划与互反馈的产品工艺方案绿色性分析

伍晓榕，张树有，裘乐淼，沈铭瑜

（浙江大学 流体动力与机电系统国家重点实验室，浙江 杭州 310027）

0 引言

工艺方案规划是连接产品设计和生产制造的重要桥梁，良好的工艺方案不仅能够为生产节约大量的时间和成本，还能降低制造对环境的污染，提高企业竞争力。由于工艺特征与加工方法的多对多映射关系、工艺设计原则的复杂多态性及制造资源的动态多样性，同一产品往往会有多个可行的备选方案［1］。因此，如何实现多个可行备选方案的有效评价和甄选，是工艺设计面临的困难之一，对于提高产品生产效率与质量具有十分重要的意义。

国内外学者对产品工艺方案决策问题进行了大量研究。文献［2］提出将层次分析法和模糊综合评判相结合，对加工零件的分层方案进行决策，从而有效避免决策的主观性；文献［3］将模糊综合评价与灰色关联分析法相结合，提出一种多工艺方案评价方法，并在某航空发动机叶片零件的工艺设计中得到应用验证；文献［4］运用工艺聚类和关联技术实现多工艺方案提取，采用不确定拓展有序加权平均算子对提取工艺方案进行评估，实现不确定语言评价下的多目标工艺方案决策；文献［5］采用蚁群算法开展多目标工艺方案的优化研究。以上研究在以时间、成本、质量为决策目标的传统工艺方案选择优化方面取得了不少成果。随着资源危机和环境污染问题的日益突出，人们越来越注重可持续发展和环境保护。传统的工艺方案选择未考虑制造的绿色性，已很难适应现代绿色制造模式的需求，工艺方案的绿色评估与选择逐渐成为国内外研究学者关注的热点。文献［6］从能源、回收性、有害性、成本和材料等目标出发，构建考虑环境意识的层次分析决策模型，提出一种绿色模糊多属性决策技术；文献［7］从绿色角度探讨了煤机零件加工工艺过程模型，研究基于绿色的煤机零件加工工艺方案的选择；文献［8］研究开发出一种面向绿色制造的工艺规划支持系统，对工艺过程中的材料消耗、能量消耗和环境排放物等进行优化，改善制造过程的绿色性；文献［9］通过构建绿色制造过程灰色模型，将工艺参数优化过程转化为多属性目标决策过程，采用DEMATEL 与VIKOR相结合的技术，提出一种绿色工艺参数的决策方法，并结合某电火花制造过程绿色工艺参数的决策对所述方法进行了说明和验证；文献［10］引入系统工程中多目标决策的密切值法，开展绿色工艺方案多目标决策。这些方法探讨了工艺与环境的关联性，并提出一些制造环境污染的有效评估技术和方法，由于工艺知识自身的多样性、复杂性、经验性及不确定性，以上方法在实际应用中还存在以下问题：

（1）工艺方案的绿色性分析是一个多目标决策过程，目前涌现了众多的研究方法，如加权和法［11］、逼近理想解法（Technique for Order Preference Similarity to Ideal Solution，TOPSIS）法［12］、层次分析法［13］、ELECTRE 法［14］、物元分析法［15］等，这些方法都需要给出各目标的决策权重，合理的权重选择对决策的准确性意义重大。然而，在决策过程中又很难定义一组恰当的且有实际物理意义的权重来保证决策的有效性和准确性，通过反复迭代的方法来探寻合理的权重又使得计算量过大甚至不可行，因此以上方法在实际应用中的操作难度较大。

（2）制造绿色性是一个较难精确度量的概念，具有一定的模糊性，其评估主要取决于决策者由自身经验知识获得的满意偏好信息，不同偏好的满意信息可能导致甄选的工艺方案差异较大，决策者满意偏好信息的缺乏使以上方法在实际应用中选出的方案不一定满足决策者要求的意愿。

（3）制造工艺评估是一个复杂的决策问题，决策者在评估初期往往无法提供全部参考信息。随着反馈给决策者的信息不断增加，决策者逐步修正工艺方案的绿色决策，从而获得最满意的结果。然而以上方法未考虑决策者与工艺方案间的互反馈，使得实际应用中缺乏决策的灵活性和满意度。

物理规划是由美国学者Messac率先提出的一种解决多目标优化决策问题的新方法［16］，该方法从决策者的主观偏好出发，通过最小化由所有决策目标构成的综合偏好函数来获得多目标决策问题的最优解，具有更大的决策合理性和简易操作性，已成功应用于优化设计、稳健设计和协同设计等方面［17-20］。本文将物理规划理论引入工艺方案的绿色性分析中，通过对用户层、满意偏好捕获层、方案决策层、方案评估层与候选方案层进行分解细化，实现工艺方案绿色性分析的多层架构，运用模糊集理论对决策者不确定、不准确的模糊知识进行处理，通过对捕获的决策者区间偏好信息进行拟合，构建真实反映决策者满意程度的偏好函数，在模糊改进的物理规划模型的基础上，提出一种反映决策者主观偏好的工艺方案互反馈绿色性分析技术，避免了传统决策方法中权重确定不合理性的缺陷，使选定工艺方案更满足决策者的主观意愿，从而提高决策的满意度。最后，结合某汽车零部件绿色工艺方案决策，对所述方法进行了应用验证。

1 工艺方案绿色性分析的多层架构

与单目标决策问题不同，多目标决策问题一般要求各个决策目标都达到最优，然而要保证这一点一般较难，特别是当目标间存在冲突时，能够满足各目标最优的解往往不存在。基于此，诺贝尔奖获得者Simon提出在某些情况下，应当用“令人满意解”来代替理论上的“最优解”，从而提出“令人满意准则”，为多目标决策问题开辟了一条新思路［21］。

定义1 对于一个待求的可行解工程问题，总是存在包含一个或多个可行解的备选解集合，如果能够找到某解或解集达到用户的满意要求，则称该工程问题为满意工程问题，而所获得的使用户满意的解或解集则称为满意解。

对于绿色制造，仅从产品质量、生产时间和成本3个目标方向进行评估决策是不够的，应该把环境影响和资源消耗作为重要因素加以考虑［22］。环境影响包括职业健康影响、生态环境破坏和职业不安全性，而资源消耗指资源种类、资源特征、资源消耗状况等。为此，工艺方案的绿色性分析应从多个目标开展决策。由于环境影响与制造效率在部分制造参数上可能存在相互竞争和矛盾，例如选择较高刀具转速进行铣削，可有效减少加工时间，提升制造效率，但随着铣刀转速的提高，工作噪声加大，切削热释放增多，加剧了环境污染。因此，各个决策目标都要求达到最优一般较难，尤其当目标间存在冲突时，最优方案可能并不存在，即绿色工艺方案决策应该是一个满意工程应用问题。

定义2 对于一个工艺方案集合的多目标决策问题，如果能够找到某个工艺方案解或方案解集，使决策者在时间、质量、成本、环境影响和资源消耗五方面都达到满意，则称使用户满意的工艺方案解或解集为绿色满意工艺方案。

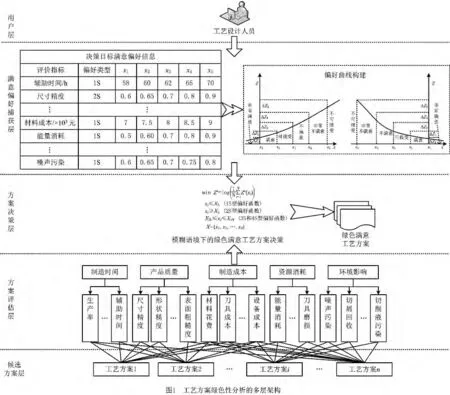
为有效实现工艺方案绿色满意度的决策，本文从满意度和绿色制造两个角度出发，将工艺方案绿色性分析分解为用户层、满意偏好捕获层、方案决策层、方案评估层与候选方案层五个层面，实现工艺方案绿色性分析的多层架构，如图1所示。该多层分析架构一方面从工艺设计人员的满意角度出发，将满意偏好捕获层分解细化为用户偏好信息的捕捉和目标偏好信息曲线的构建，实现决策者满意偏好的提取。另一方面，从绿色制造的角度出发，分解细化制造成本、产品质量、环境影响等绿色制造评估指标，如制造成本分解细化为材料花费、刀具成本和设备成本等方面，从而构建完整的评估指标体系。最后，将方案决策层分解细化为绿色评估表达、满意决策模型构建和绿色满意方案求解等步骤，结合捕获的决策满意偏好信息，开展工艺方案集的绿色满意度决策。

2 满意偏好函数

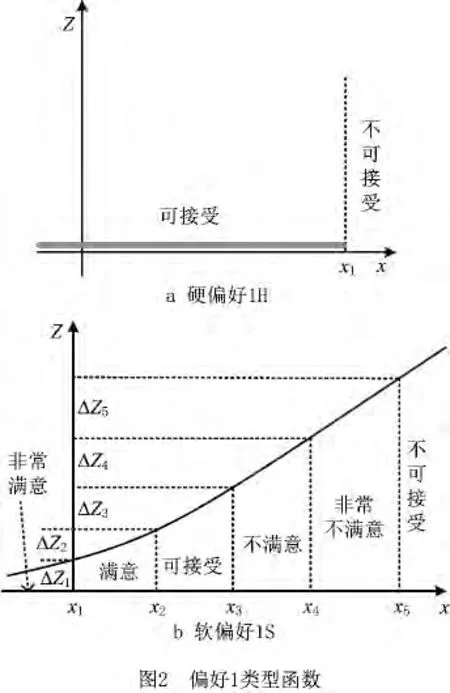
满意偏好指决策者依赖自身事先掌握的知识，对决策问题的某个目标进行主观意愿的折衷表达。如果能够捕获到决策者的主观满意偏好信息，就能对决策问题中无法比较的有效解进行评估，从而获得令决策者满意的可行解。满意偏好函数是决策目标的函数，它以决策目标为自变量，以决策者的满意度为因变量，反映了决策者对于给定目标的满意程度。该函数主要分为4种类型，用数字1～4表示，每种类型根据满意精度的不同又可细分为“软”和“硬”两种情况，分别用S和H 来表示。对于所有类型的偏好函数，都是取值越小表示决策者对设计目标越满意。图2a为硬偏好1H 函数，它将设计目标分为可接受和不可接受两个区间；图2b为常用的软偏好1S函数，它将设计目标划分为不可接受、非常不满意、不满意、可接受、满意和非常满意六个不同的满意程度区间。图2中，xi为决策者根据自身经验和知识认为的各个区间边界值，纵坐标Z为决策者的满意程度，其他偏好函数类型详见文献［23］。

由图2可知，硬偏好函数具有较强的突变跳跃性，由于人类思维和决策是一个渐进的过程，通常采用软偏好函数来定义决策者的偏好，本文在文献［16］与文献［24］研究的基础上，以偏好函数1S为例来叙述其求解过程，其他类型偏好函数的求解可参照类似步骤进行。偏好函数1S的求解步骤为：

步骤1 研究决策指标的性质，确定偏好函数的类型，如对于成本型指标，偏好函数选为1S类型，决策者根据自身经验知识和当前制造状况，给出决策指标满意区间划分的边界判定值Xi。

步骤2 获取决策者满意度的区间增量

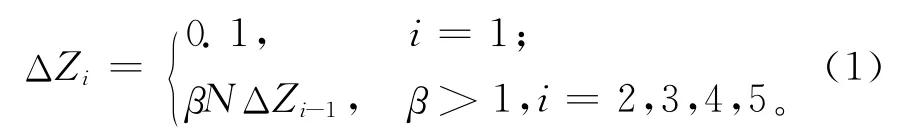
式中：N为决策目标的总数目，β为大于1的满意度参数，选取原则和方法参见文献［16］。

步骤3 求解决策指标不同满意区间边界的偏好函数值

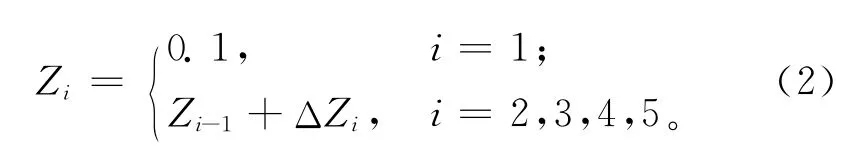
步骤4 求解决策指标不同满意区间边界的偏好函数导数值

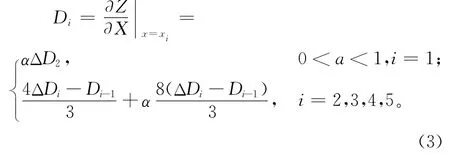
式中：α为小于0.1的常系数，选取原则和方法参见文献［16］；ΔDi为决策指标第i段的平均斜率，

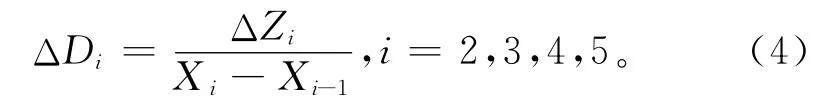
步骤5 对决策指标偏好分段区间边界值及其导数，采用分段函数进行拟合，获得决策者的偏好函数Z=f（x），

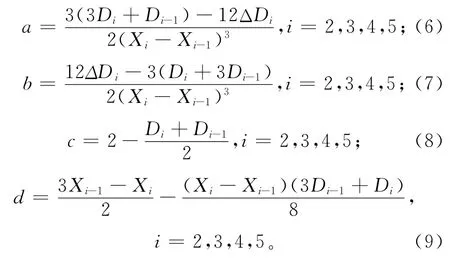
3 工艺方案绿色性分析

3.1 绿色评估的模糊表达

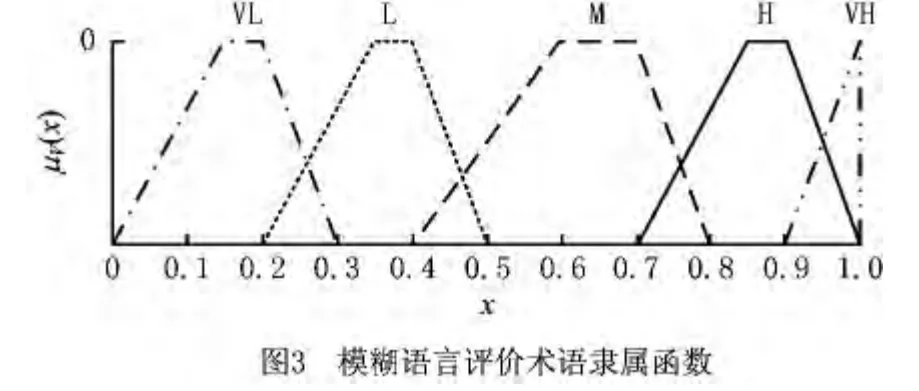
考虑到绿色评估结果的模糊性，将评价因子看作是模糊语言变量，应用模糊集理论，结合专家知识和经验，建立各语言变量的模糊语言评估术语集V=｛v1，v2，v3，v4，v5｝=｛很高（VH），高（H），一般（M），较低（L），极低（VL）｝。因模糊数的形式多样，通常采用三角模糊数和梯形模糊数，由于三角模糊数可视为梯形模糊数的特殊形式，这里采用较为通用的梯形模糊数对模糊语言术语进行量化处理，表示为vi=（a1，a2，a3，a4），i=1，2，…，5，其中a1＜a2＜a3＜a4，隶属度函数表示为

经专家组评定，其模糊语言集的隶属函数如图3所示。这样，当专家对绿色方案采用模糊语言变量进行评估时，就可以通过以上方式将评估语言转换成模糊数。

3.2 模糊物理规划的工艺方案满意决策模型

考虑到绿色工艺评估结果较多地依赖于专家模糊的经验与知识，运用模糊集理论对物理规划模型进行改进，构建基于模糊物理规划的工艺方案满意决策模型。

根据3.1节中的模糊表达方法，对于绿色工艺的模糊语言评估结果，可用梯形模糊数进行量化处理，因此对应的决策偏好信息也是梯形模糊数，可表示为

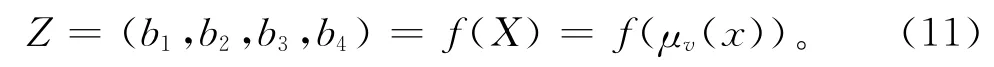
模糊数的反模糊化是对模糊偏好信息进行比较排序的基础，国内外众多学者对该问题进行了深入研究，提出许多有效的方法，本文选择Sugeno提出的重心法［25］，公式如下：

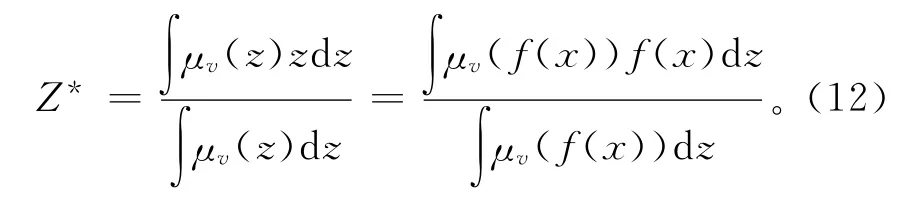
式中Z＊表示与工艺决策目标模糊偏好信息Z相对应的偏好函数值。

将各个设计目标偏好函数综合起来，就可以得到综合模糊偏好函数。综合的方法有许多，一般采用平均值的对数。基于模糊偏好信息表达与反模糊化技术，参考物理规划的决策模型，构建模糊语境下的工艺方案满意决策模型：

求解该决策模型，即可获得最终的满意工艺方案。

3.3 工艺方案满意决策的互反馈机制

产品制造工艺决策经常受到人员、物料、设备等动态因素的影响，即便是同一决策者，对于同一决策问题在不同时期或场合可能会作出重大调整，决策者不同的偏好往往会导致不同的工艺方案排序，这就要求决策者能够参与到决策过程中，通过不断改变和调整形成新的偏好来进行反复决策，直到对方案排序结果满意为止。产品制造工艺决策的实质是以工艺设计人员的决策偏好为输入，以决策者满意工艺方案为输出的互反馈过程，通过交互方式获取工艺设计人员对于工艺方案不同决策目标的偏好信息，构建各决策目标的满意偏好曲线，运用模糊语境下的满意工艺决策模型开展工艺方案的绿色满意度分析，将选定的工艺方案形象化为决策目标满意图，并反馈给工艺设计人员，以便工艺设计人员在结合其他工艺资源信息的基础上修改偏好信息，重新进行方案评估，从而通过满意度判断在决策者与工艺方案之间形成一个互反馈过程，如图4所示。

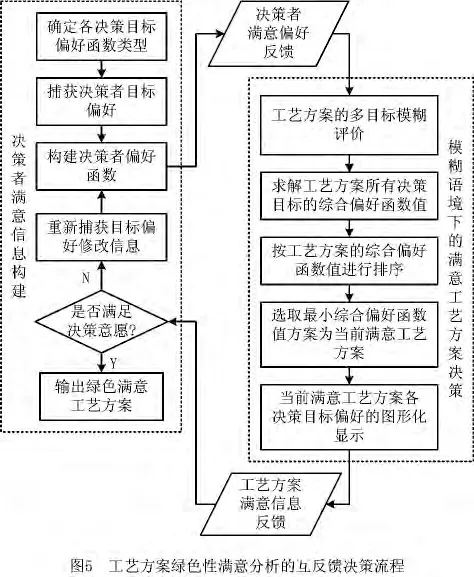
3.4 分析流程

根据绿色方案决策模型，同时考虑决策过程的互反馈机制，获得基于模糊物理规划与互反馈的满意工艺方案绿色性分析流程如图5所示，主要实施步骤如下：

步骤1 决策者针对决策目标，确定偏好函数的类型。

步骤2 通过交互方式捕获工艺设计人员对于工艺方案不同决策目标的偏好信息。

步骤3 根据捕获的决策者偏好信息，采用分段函数进行拟合，通过式（1）～式（9）构建各决策目标的偏好函数。

步骤4 将决策者的满意偏好反馈到工艺方案评估决策过程中。

步骤5 决策者运用模糊语言对工艺方案进行多目标评估，获得不同工艺方案的各决策目标评估值。

步骤6 通过反馈的满意偏好函数，依据式（10）～式（12）求解各决策目标的满意度，并通过式（13）得到综合考虑所有决策目标的综合偏好函数值。

步骤7 对不同工艺方案按照综合偏好函数值进行排序。

步骤8 依据工艺方案满意决策模型，通过式（13）～式（15）求解获得最小综合偏好函数值方案，作为当前满意工艺方案。

步骤9 将当前满意工艺方案各决策目标偏好进行图形化显示。

步骤10 将当前满意工艺方案各决策目标的满意信息反馈给决策者，以便他们对当前满意工艺方案做出决择。

步骤11 如果当前满意工艺方案各决策目标的偏好情况不满足决策者的意愿，则重新捕获决策目标的修改偏好信息，转步骤3。

步骤12 如果当前满意工艺方案各决策目标的偏好情况满足决策者的满意偏好意愿，则输出当前选定的工艺方案，作为最满意的绿色工艺方案，结束决策过程。

4 实例应用

汽车工业作为一个重大的制造领域，其绿色制造的程度对于减少整个制造业污染排放、保护生态环境具有极其重要的意义，而工艺的选择与实施是实现绿色制造的关键。本文从决策者的主观偏好优化角度，考虑制造加工的环境影响，利用所提出的理论和方法，开展某汽车零配件××型后门门框产品的绿色工艺方案决策。该产品的3D 数模如图6所示。根据制造经验及工艺原理，可拟定以下四种核心工艺路线，如表1所示。采用图1工艺方案绿色性分析多层架构中的方案评估指标对有效工艺方案集S=｛s1，s2，s3，s4｝开展绿色性评估，所得模糊性能评估结果如表2所示。

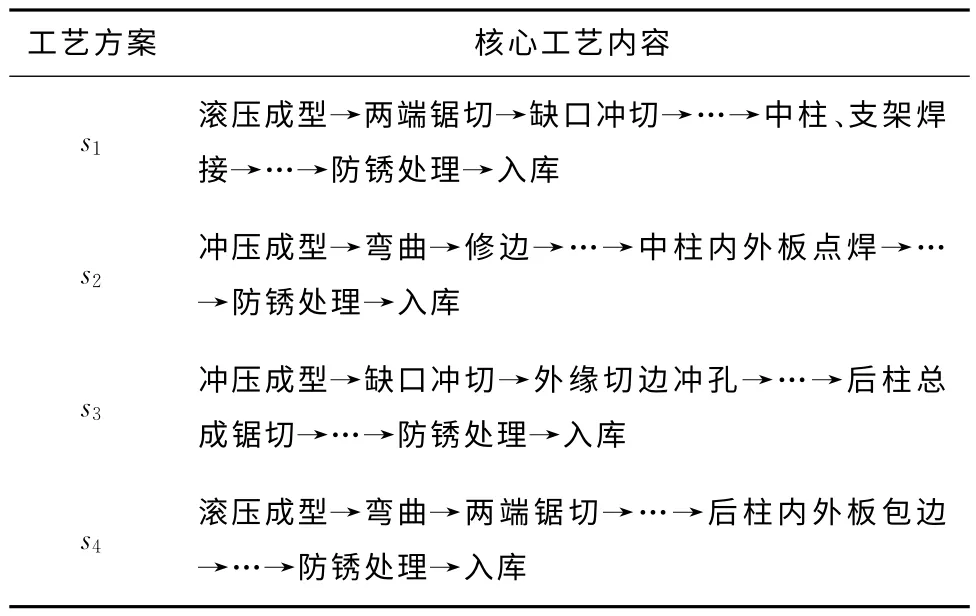
表1 后门门框核心工艺方案

表2 ××型号后门门框工艺方案的绿色性评估

决策者根据自身经验与知识，给出工艺方案各绿色评价指标的偏好信息，如表3中决策1的数据。根据捕获到的决策者满意偏好信息，按照式（1）～式（9）构建出评估指标的偏好函数。如对于制造成本目标，在参数α=0.09，β=1.5的条件下构建的偏好函数为

式中zi表示x∈（xi-1，xi］的分段函数表达式。

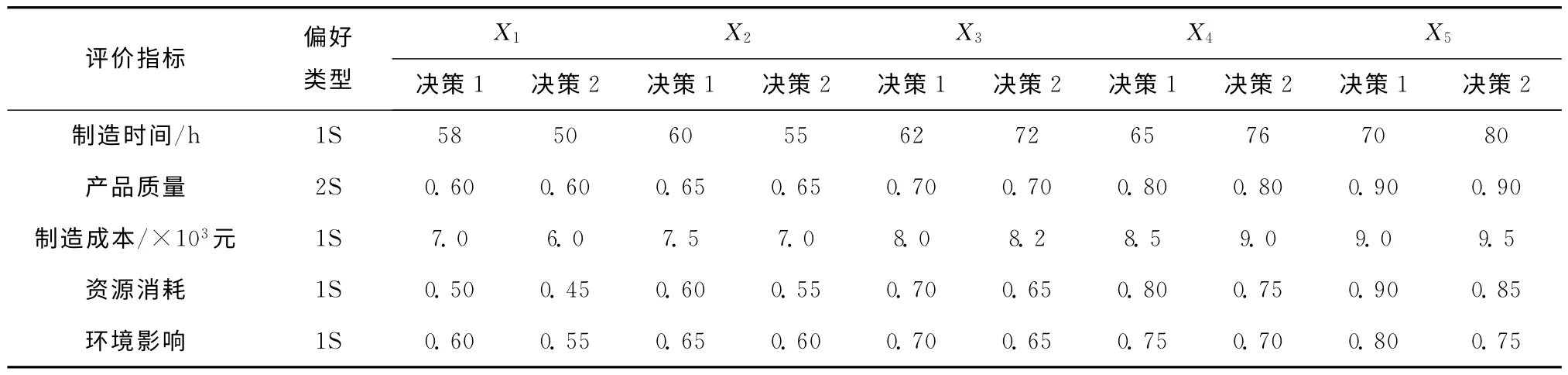
表3 工艺方案绿色性评估指标的偏好信息

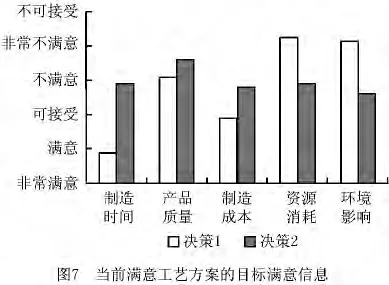
将工艺方案si的预测目标值代入相应决策目标的偏好函数，求解出相应的偏好值，并根据式（13）～式（15）进行综合，最终获得工艺方案si的综合偏好值，如表4中的决策1所示。由表4可知，工艺方案s3的综合偏好函数值最小，因此为当前绿色满意工艺方案，它在当前决策者满意偏好下的满意程度如图7中的决策1所示。

表4 工艺方案绿色性分析

将当前工艺方案各决策目标的满意信息（如图7中的决策1）反馈给决策者，以便其对当前的满意工艺方案做出决择。如图7所示，在决策1中，方案s3的资源消耗和环境影响较高，如果决策者对该结果不满意，则可以适当牺牲其他目标（如制造时间和制造成本），以换取更好的能源消耗满意。为此，决策者重新修改偏好信息（表3 中决策2 对应的数据），并将新的决策满意偏好反馈到工艺方案评估决策过程中，开展第2次工艺方案决策。按表3中的决策2偏好信息进行捕获后，再对所有的工艺方案进行评估，这时得到的结果如表4中的决策2所示。该情况下，工艺方案的决策偏好如图7中的决策2条纹线所示。由表4和图7可知，此时最满意的工艺方案为s4，从而在决策者与工艺方案间的满意信息互反馈的基础上，实现了工艺方案绿色满意度的决策。

目前，本文所述的产品工艺方案绿色性分析技术已初步应用于某汽车零部件生产企业的智能计算机辅助工艺设计系统中，可视化操作界面如图8所示，图中：①通过对决策目标偏好信息边界值的获取来构建决策者的偏好曲线，捕获到决策者的目标偏好信息；②对多个可行工艺方案开展绿色性评估，运用模糊物理规划的工艺方案满意决策模型获得不同工艺方案的绿色性优先次序；③将工艺方案绿色性分析结果以图形化的形式反馈给决策者，对于当前工艺方案中非常不满意的决策目标会以红色进行警示，决策者可根据方案反馈信息对决策偏好信息进行调整，从而为工艺方案绿色满意度决策提供科学实际的指导。

5 结束语

绿色制造是当前制造业的一种全新可持续制造模式，工艺方案的绿色性分析是实现绿色制造的关键。本文提出一种面向绿色制造的满意工艺方案分析技术，其主要工作与特点包括：

（1）通过分解细化用户层、满意偏好捕获层、方案决策层、方案评估层与候选方案层，实现工艺方案绿色性分析的多层架构，提出一种工艺方案满意决策的规划思路。

（2）通过偏好函数表达决策者依赖于自身经验知识产生的主观偏好信息，避免多目标决策中各目标权重难定义的问题，提出绿色满意工艺方案的概念，使选出的方案更加满足决策者的意愿，从而提高方案的满意度。

（3）通过在决策者与工艺方案间构建满意信息的互反馈，使决策者主动参与到决策过程中，实现工艺方案的绿色互反馈决策，提高决策灵活性。以××型号后门门框工艺方案决策为例，对所提方法进行验证，获得了满意的绿色工艺方案，提高了决策的满意度。

基于文中所提出的产品工艺方案绿色性分析方法，下一步将研究复杂产品工艺方案的绿色优化技术，为面向绿色制造的产品工艺设计提供支持。

［1］CHENG Guangyao，SUN Houfang，LEI Hegong，et al.Fuzzy synthetic estimation of multi-process planning schemes in CAPP［J］.Journal of Beijing Institute of Technology，2004，24（3）：197-200（in Chinese）.［程光耀，孙厚芳，雷贺功，等.CAPP多工艺设计方案的模糊综合评价［J］.北京理工大学学报，2004，24（3）：197-200.］

［2］ZHANG Jianfeng，PENG Anhua.Decision-making of slicing scheme in fused deposition modeling process based on analytical hierarchical process［J］.Transactions of Nanjing University of Aeronautics &Astronautics，2010，27（2）：125-130..

［3］WANG Pei，ZHANG Dinghua，CHEN Bing，et al.Evaluation of multi-process plans based on fuzzy comprehensive evaluation and grey relational analysis［J］.Journal of Aerospace Power，2012，27（9）：2075-2085（in Chinese）.［王 佩，张定华，陈 冰，等.基于模糊综合评价与灰色关联分析法的多工艺方案评价［J］.航空动力学报，2012，27（9）：2075-2085.］

［4］FANG Hui，YIN Guofu，GAO Wei，et al.Uncertain language multi-attribute decision-making method for process scheme evaluation［J］.Computer Integrated Manufacturing Systems，2006，12（11）：1894-1898，1915（in Chinese）.［方 辉，殷国富，高 伟，等.工艺方案评价的不确定语言多属性决策研究［J］.计算机集成制造系统，2006，12（11）：1894-1898，1915.］

［5］LIU X，YI H，NI Z.Application of ant colony optimization algorithm in process planning optimization［J］.Journal of Intelligent Manufacturing，2013，24（1）：1-13.

［6］KUO T C，CHANG S H，HUANG S H.Environmentally conscious design by using fuzzy multi-attribute decision-making［J］.The International Journal of Advanced Manufacturing Technology，2006，29（5）：419-425.

［7］LIU Yu.Selection of process parts of mining machinery based on green［J］.Coal Mine Machinery，2007，28（7）：107-108（in Chinese）.［刘 羽.基于绿色的煤机零件加工工艺方案的选择［J］.煤矿机械，2007，28（7）：107-108.］

［8］HE Y，LIU F，CAO H J.Process planning support system for green manufacturing and its application［J］.Frontiers of Mechanical Engineering in China，2007，2（1）：104-109.

［9］WU Xiaorong，ZHANG Shuyou，QIU Lemiao，et al.Decision making method of process parameter selection for green manufacturing based on a DEMATEL-VIKOR algorithm［J］.Journal of Mechanical Engineering，2013，49（7）：91-100（in Chinese）.［伍晓榕，张树有，裘乐淼，等.面向绿色制造的加工工艺参数决策方 法及应 用［J］.机械工程学报，2013，49（7）：91-100.］

［10］HAN Ziqiang，YUE Wenhui，WANG Xiaojun.An application researching of osculating value method in decision-making of green processes schemas［J］.Equipment Manufacturing Technology，2012（9）：63-65（in Chinese）.［韩自强，岳文辉，王晓俊.密切值法在绿色工艺方案决策中的应用［J］.装备制造技术，2012（9）：63-65.］

［11］HWANG C L，YOON K.Multiple attribute decision making［M］.Berlin，Germany：Springer-Verlag，1981.

［12］LAI Y J，LIU T Y，HWANG C L.Topsis for MODM［J］.European Journal of Operational Research，1994，76（3）：486-500.

［13］CHOWDARY V M，CHAKRABORTHY D，JEYARAM A，et al.Multi-criteria decision making approach for watershed prioritization using analytic hierarchy process technique and GIS［J］.Water Resources Management，2013，27（10）：3555-3571.

［14］FIGUEIRA J R，GRECO S，ROY B，et al.An overview of ELECTRE methods and their recent extensions［J］.Journal of Multi-Criteria Decision Analysis，2012，20（1）：61-85.

［15］FANG Guohua，HUANG Xianfeng.Multiobjective decision making：theory，methods and applications［M］.Beijing：Science Press，2011（in Chinese）.［方国华，黄显峰.多目标决策理论、方法及其应用［M］.北京：科学出版社，2011.］

［16］MESSAC A.Physical programming-Effective optimization for computational design［J］.AIAA Journal，1996，34（1）：149-158.

［17］HUANG Hongzhong，TIAN Zhigang，GUAN Liwen.Neural networks based interactive physical programming and its application in mechanical design［J］.Chinese Journal of Mechanical Engineering，2002，38（4）：51-57（in Chinese）.［黄 洪钟，田志刚，关立文，等.基于神经网络的交互式物理规划及在机械设计中的应用研究［J］.机械工程学报，2002，38（4）：51-57.］

［18］TAPPETA R V，RENAUD J E，MESSAC A，et al.Interactive physical programming：tradeoff analysis and decision making in multicriteria optimization［J］.AIAA Journal，2000，38（5）：917-926.

［19］MESSAC A，ISMAIL-YAHAYA A.Multiobjective robust design using physical programming［J］.Structural and Multidisciplinary Optimization，2002，23（5）：357-371.

［20］MCALLISTER C D，SIMPSON T W，HACKER K，et al.Integrating linear physical programming within collaborative optimization for multiobjective multidisciplinary design optimization［J］.Structural and Multidisciplinary Optimization，2005，29（3）：178-189.

［21］ZHANG Xu.Study on models and methods of fuzzy multiobjective optimization with indeterminacy of DM［D］.Dalian：Dalian University of Technology，2009（in Chinese）.［张 旭.决策信息不明确的多目标模糊优化模型与方法［D］.大连：大连理工大学，2009.］

［22］LIU Fei，ZHANG Hua，CHEN Xiaohui，et al.A decision making framework model of green manufacturing［J］.Chinese Journal of Mechanical Engineering，1999，35（5）：11-15（in Chinese）.［刘 飞，张 华，陈晓慧，等.绿色制造的决策框架模型及其应用［J］.机械工程学报，1999，35（5）：11-15.］

［23］MESSAC A，WILSONT B.Physical programming for computational control［J］.AIAA Journal，1998，36（2）：219-226.

［24］DONG Shuge，RAO Qilin.Physical programming theory based on preference design［J］.Journal of University of Science and Technology Beijing，2009，31（2）：250-255（in Chinese）.［董书革，饶绮麟.基于偏好设计的物理规划理论［J］.北京科技大学学报，2009，31（2）：250-255.］

［25］SUGENO M.An introductory survey of fuzzy control［J］.Information Sciences，1985，36（1）：59-83.