雷达组网多传感器选择快速启发式算法
2014-12-02
(杭州电子科技大学信息与控制研究所,浙江 杭州310018)
0 引 言
随着现代战争环境日益复杂,防空预警体系通过配置多个传感器组网进行协同探测,可提高对目标的探测和跟踪效果[1]。在跟踪系统中引入传感器管理是在跟踪性能和系统资源之间建立一种平衡,以达到系统整体性能最优[2]。传感器管理技术的核心问题是依据一定的准则,对传感器资源进行优化分配[3]。目前主要有基于线性规划论[4]、基于信息论和基于协方差控制[5-7]的传感器管理方法。但是由于组网中传感器数目的增加,带来传感器选择算法计算量过大的问题。于是便有了贪婪算法[5]的提出,但是该算法对传感器的选取过于保守,导致频繁选择了精度过高的传感器。本文提出了一种快速多传感器选择算法。本方法以控制协方差水平的思想对传感器进行管理,在线通过每次选取期望最接近期望增益的传感器形成探测某目标的传感器组合,在满足目标跟踪精度的前提下,减少了算法的计算量。
1 系统模型
目标的运动方程和量测方程为X(k)=FX(k-1)+Gw(k-1)和Zi(k)=HiX(k)+vi(k)。其中i=1,…,N,X(k)是k时刻的目标状态向量,Zi(k)是k时刻传感器i 对目标的量测值,w(k)是系统噪声,vi(k)是第i个传感器的量测误差,都是高斯噪声且均值为零。Q和Ri是相应的协方差矩阵。F为状态转移矩阵,G为输入分布矩阵,Hi为传感器i的观测矩阵,N为跟踪系统中的传感器个数。对于这样一个系统,传感器的组合数可以达到2N-1种。假设第s个传感器组合用Ds表示,每个组合中的个数用Ns表示,那么对于给定的第s个组合,其序贯卡尔曼滤波的主要过程为:先对第一个传感器做一次卡尔曼滤波,接着从第二个传感器开始依次将前一个传感器的滤波结果,即状态估计值作为下一个传感器滤波的预测值。
在多传感器跟踪融合中,协方差的递推更新表达式如下:
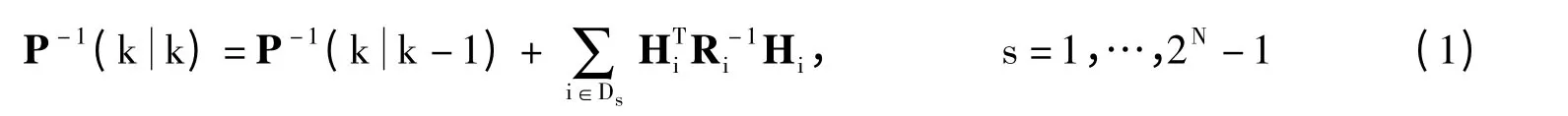
状态估计的更新过程通常采用上述的逆协方差形式,这种形式又称为信息矩阵。定义传感器组合Ds的信息增益Js为:
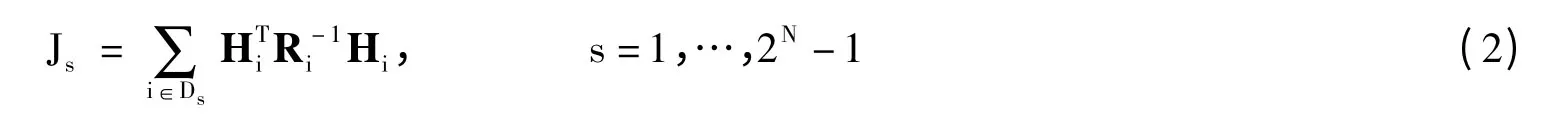
由式(2)可知,在不同的观测噪声下,各传感器的信息增益不同。
2 传感器选择算法
2.1 基于协方差控制的传感器选择算法
在组网系统中,传感器资源相对比较丰富,所以对系统内的传感器资源在跟踪模式下做选择时很有必要的。一方面可以提高组网的跟踪性能,另一方面在满足跟踪精度的要求下,可节省系统资源。

然而使式(3)达到最小的传感器组合并不一定是控制实际协方差逼近期望协方差的最优传感器组合。为此,采用基于协方差控制的策略进行传感器分配传感器资源,其基本思想是对每个目标预先设定一个期望的跟踪精度Pd(k),即期望协方差阵,控制传感器在某种度量及准则下使实际协方差在某种意义上逼近Pd(k)。目标函数为:

2.2 传感器选择快速启发式算法
传感器选择问题可描述为一个组合优化问题。以前对于传感器组合的选择一般都需要遍历组网中所有的传感器组合,假设组网中有N个传感器,那么遍历步长则为2N-1步,其计算复杂度为O(2Nn3)。所以增加组网中的传感器数量,计算量会显著增加,全遍历寻优方式存在组合爆炸问题。为了减少计算量,本文提出一种贪婪启发式算法,算法的主要思想是基于期望信息增益的思想,每次选取一个“最佳”的传感器形成探测某目标的传感器组合,通过一系列的贪婪选择当前状态下的最优选择,逐步逼近给定的目标,直到满足跟踪精度要求。
算法结合协方差控制传感器管理方法的概念,引入“期望信息增益”概念,动态计算各传感器的期望信息增益,根据式(2)可计算出各传感器观测目标时的信息增益:


根据各传感器接近期望信息增益的程度对传感器进行排序,在线通过每次选取期望最接近期望增益的传感器形成探测某目标的传感器组合。排序目标函数如下:

根据每个时刻的排序结果,利用协方差思想可以选出当前时刻使的对角阵的最小值大于零的传感器组合D(k),这便是当前时刻作为滤波跟踪的传感器组合。
与传统协方差控制相比,本方法中待选的传感器组合数为M个,而传统协方差控制中待选传感器组合个数为2M-1。同时本算法无需遍历所有传感器组合,当某种组合下跟踪精度满足时,停止搜索。本算法保证在满足跟踪精度的前提下,大大减小了计算量。克服了基于信息论传感器管理方法片面追求信息量最大的缺点,满足系统对跟踪精度要求的前提下,可以尽可能地节省资源。
3 仿真结果与分析
仿真场景参考文献[8]。将本文提出的快速启发式算法与传统协方差控制算法和贪婪算法进行比较,使用Monte Carlo仿真,仿真测试为50次。经过50次Monte Carlo仿真,贪婪算法和快速启发式算法的平均计算时间为0.001 1 s和0.001 4 s,而传统的协方差控制算法的平均耗时为0.499 5 s,可以发现算法在减少计算量上取得了明显的效果。
3种算法各时刻的雷达选择情况如图1所示。由图1可知传统协方差控制算法在传感器选择上出现明显的切换情况,贪婪算法在稳定后没有出现切换,快速启发式算法在稳定后传感器2和6 之间有切换。而且在前50 s 快速启发式算法比贪婪算法只多选了一个传感器,在后50 s 快速启发式算法虽然与传统协方差控制算法都选择了5个传感器,但是明显稳定了许多。
3种算法的滤波协方差与期望协方差的一个相互比较如图2所示,控制效果最好的自然是传统的协方差控制算法,但是它的耗时大大降低了其实用性。其他两种算法中,都具有耗时短实用性强的特点,但是快速启发式算法的协方差控制效果与期望的差距明显小于贪婪算法,控制效果的提高体现了在选择最好传感器的准则的改变是可行的。
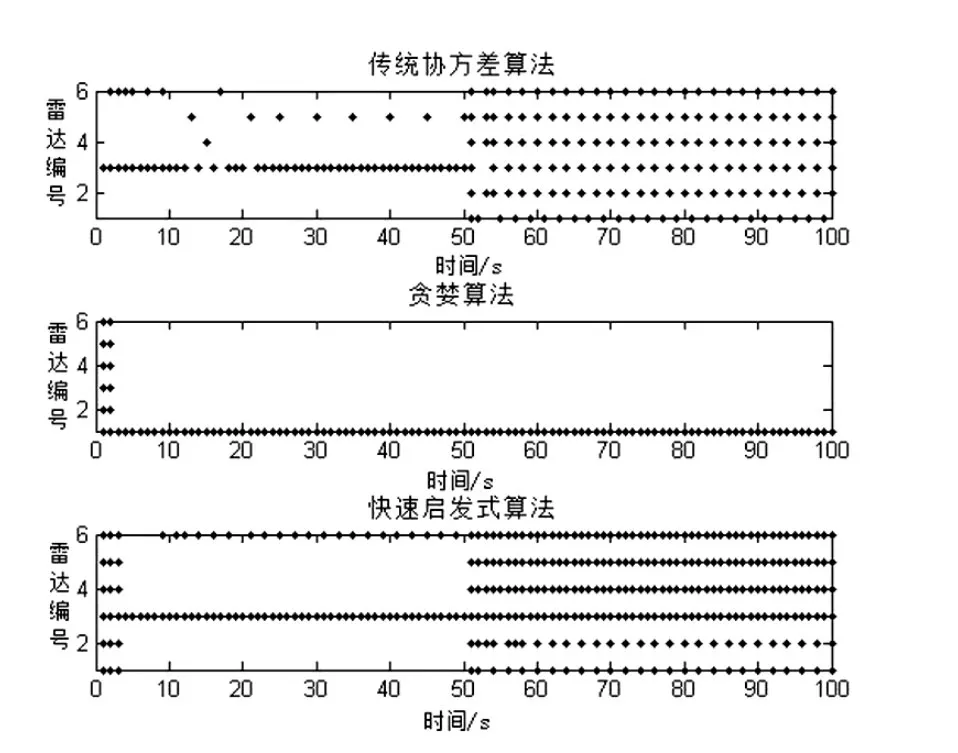
图1 3种算法各时刻的雷达选择情况
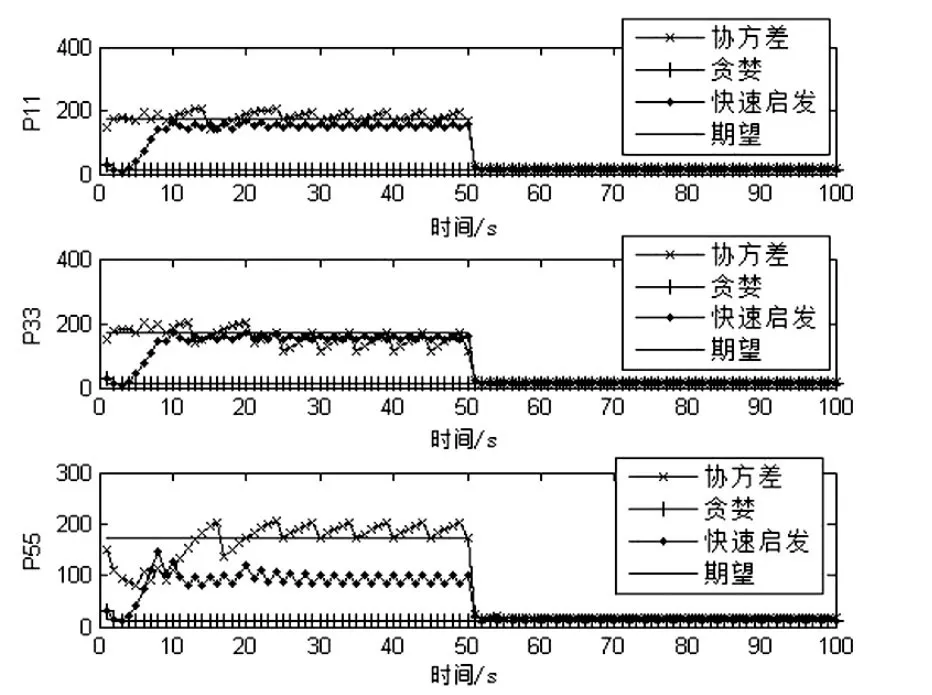
图2 3种算法的位置协方差比较
4 结束语
传统的协方差控制算法由于计算量太大常不能应用于实际系统中,贪婪算法和快速启发式算法降低了传感器选择算法中计算的复杂度,具有很强实用性,这也是降低传感器选择算法的一种趋势。在这个趋势下,可以通过选取某种更好地贪婪准则使其即快速又准确的选择与最优组合更接近的传感器组合。本文讨论的多传感器快速选择算法比贪婪算法增加计算量很少,并且可以找到一个更优的传感器组合,使滤波协方差更接近期望协方差水平。所以它具有贪婪算法的计算效率,同时获得比贪婪算法具有更好性能。
[1]叶朝谋,丁建江,李庭胜,等.雷达探测资源管理技术分析与评估[J].现代雷达,2012,34(3):6-11.
[2]田康生,朱光喜.目标跟踪中的传感器管理[J].传感器技术,2003,22(3):27-29.
[3]何友,王国宏,关欣.信息融合理论及应用[M].北京:电子工业出版社,2010:444-447.
[4]Xiong N,Svensson P.Multi-sensor management for information fusion:issues and approaches[J].Information Fusion,2002,3(2):163-186.
[5]Kalandros M,Pao L Y.Controlling Target Estimate Covariance in Centralized Multisensor Systems[C].Philadelphia:American Automatic Control Council,1998:2 749-2 753.
[6]周文辉,胡卫东,余安喜,等.基于协方差控制的集中式传感器分配算法研究[J].电子学报,2003,31(12):2 158-2 162.
[7]杨秀珍,何友,鞠传文.基于跟踪精度控制的传感器管理方法研究[J].电光与控制,2005,12(1):9-11.
[8]韩海峰,周文辉,陈国海.目标跟踪中期望协方差控制的分布式多传感器管理[J].现代雷达,2007,29(1):47-51.
