美式期权定价模型的高阶紧差分方法*

于国晓，谢树森

（中国海洋大学数学科学学院，山东 青岛 266100）

期权定价理论的创建是近几十年金融领域中最重要的发展之一。相对于欧式期权，美式期权可以提前实施，拥有更多的获利机会，操作具有更大的灵活性，应用更为广泛，研究美式期权定价模型的数值方法更具有实际意义。关于美式期权定价问题数值方法研究已有很多工作，例如二叉树方法［1］，有限元方法［2］、惩罚函数法［3］、移动边界法［4］等。

美式期权定价模型最终归结为一个自由边界问题。本文对支付红利的美式买入期权模型实施Frontfixing变换［5］，将自由边界问题转化为一个非线性的定边界问题，构造三层紧致差分格式对此非线性问题进行离散并进行数值实验。与二叉树方法［1］和一般差分方法［5］的数值结果比较证明本文算法是有效的。

1 美式买入期权定价模型

本文考虑由Black-Scholes方程推广得到的支付红利的美式买入期权模型。用C（S，t）表示美式买入期权价格，由文献［2］可知美式买入期权定价模型如下：

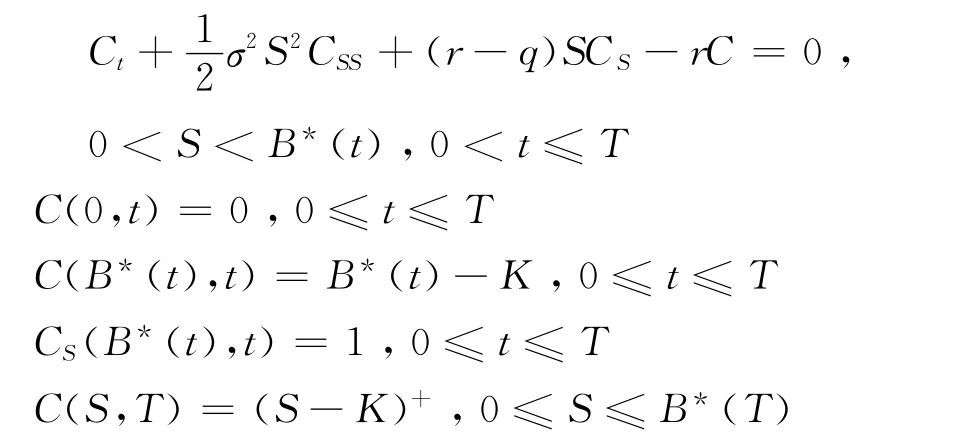
其中：S为标的资产价格，K为期权的执行价格，T为期权的执行时间，r为无风险率，q为期权执行期间的红利率，σ为标的资产价格波动率，z＋＝max（z，0），自由边界B＊（t）是最优执行边界，且B＊（t）是未知的。本文进一步假设世界风险是中性的，即q＞0。当S在t时刻小于B＊（t），期权应该持有，而当S在t时刻大于或等于B＊（t）时，期权应该被执行，即C（S，t）＝SK。

令τ＝T－t，B（τ）＝B＊（T－τ），则上述倒向问题变换为如下正向初边值问题：

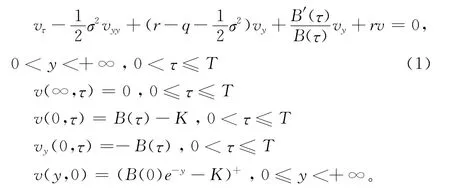
上述变量替换成立，当且仅当B（τ）＞0。文献［6-7］中说明B（τ）是关于τ的非负单调增函数，并给出了B（τ）的取值范围B（0）≤B（τ）≤KX，其中

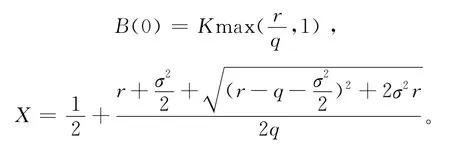
引理1［2］对于给定的正实数ξ∈ （0，1），有

C（S，t）≤ξ，0≤S≤Ke－Y，0≤t≤T

其中：

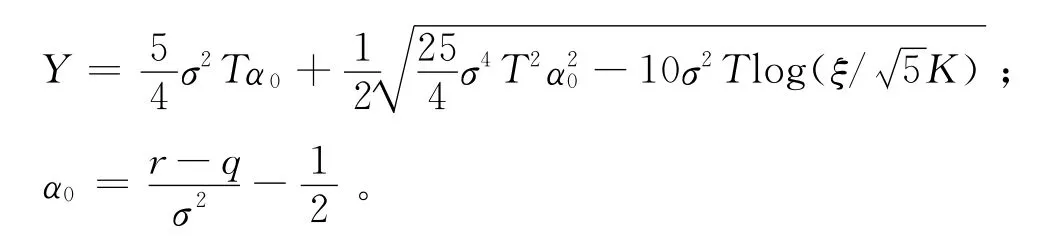
2 高阶紧致差分格式

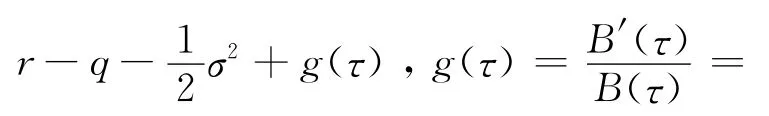
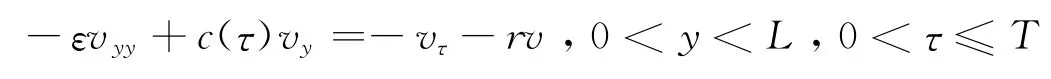
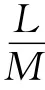
令－εvyy＋c（τ）vy＝f。记为函数v在结点（yj，τn） 处 的 值，。由Taylor展开式得

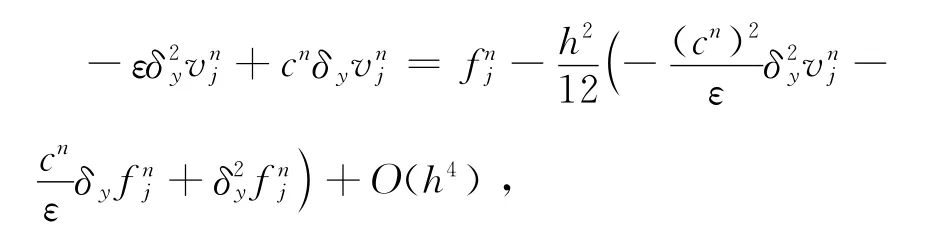
整理

令f＝－vτ－rv，可以得到

记表示的近似值，略去上式中的截断误差得到如下紧致差分方程：

差分格式（7）的截断误差为O（h4＋k2）。（7）式等价记为：

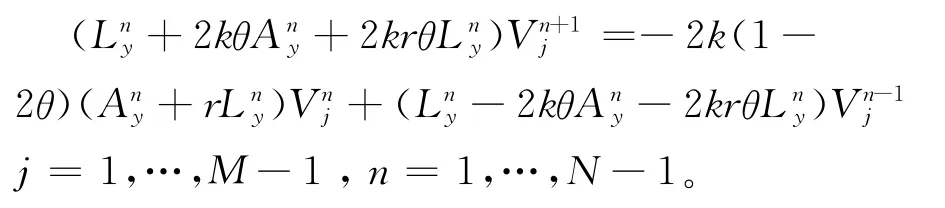
利用Fourier方法，增长矩阵的特征值的模均小于等于1，差分格式是稳定的。

下面讨论边界条件的差分离散。设上述紧致差分方程在j＝0时成立，即

又由边界条件（5）直接四阶差分离散可得：

由式（8）和（9）消去，整理可得

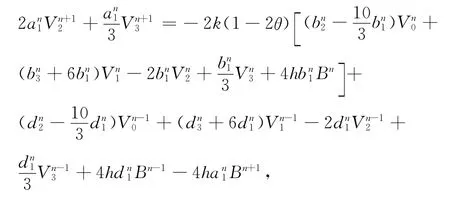
其中：

Bn＋1使用Bn，Bn－1，Bn－23点的插值逼近，即

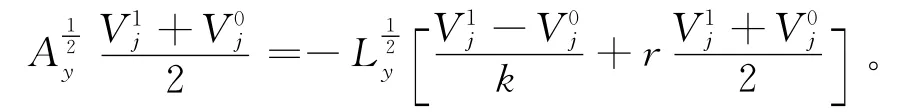
3 数值实验

算例1 取参数K＝10，r＝0.03，q＝0.07，σ＝0.2，T＝1，θ＝0.5。表1给出不同步长期权价格C（S，t）近似解。并与二叉树方法的数值结果［8］进行比较。可以看出紧致差分方法是收敛的。

表1 在t＝0时，不同空间、时间步长下的美式买入期权价格（C）Table 1 Values of an American call option by different mesh size at t＝0

算例2 取参数K＝10，r＝0.1，q＝0.05，σ＝0.2。由于美式买入期权没有精确解，为了比较误差，取文献［5］中差分方法在步数分别取N＝4 096，M＝4 000所到的数值解为精确解v。

图1～6，取θ＝0.5，给出T取不同值时，自由边界B（τ）与B＊（t）数值解曲线，图中exact表示文献［5］中差分方法取N＝4 096，M＝4 000得到的自由边界曲线。

图7、8分别给出取θ＝0.5，T＝1时，函数V（y，T）和美式期权C（S，0）的数值解。

图9、10分别给出θ＝0.5，T＝1，N＝64，M＝80时，函数V（y，τ）和期权价格C（S，t）的数值解。

表2给出T＝1时，紧致差分方法取不同θ值的误差与收敛阶。由数据可以看出θ取不同值时，误差略有差异，紧致差分方法虽然达不到4阶精度，但数值结果都要比文献［5］差分法好得多。

表3给出自由边界B（τ）计算较精确的情况下，紧 致差分法的收敛阶可以达到接近四阶。

图1 T＝0.5时，自由边界B（τ）图像Fig.1 Early exercise price B（τ）at T＝0.5

图2 T＝1时，自由边界B（τ）图像Fig.2 Early exercise price B（τ）at T＝1

图3 T＝3时，自由边界B（τ）图像Fig.3 Early exercise price B（τ）at T＝3

图4 T＝0.5时，自由边界B＊（t）图像Fig.4 Early exercise price B＊（t）at T＝0.5

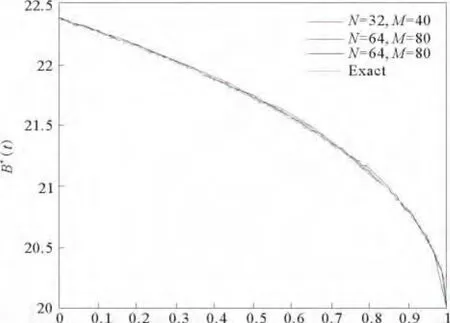
图5 T＝1时，自由边界B＊（t）图像Fig.5 Early exercise price B＊（t）at T＝1

图6 T＝3时，自由边界B＊（t）图像Fig.6 Early exercise price B＊（t）at T＝3

图7 τ＝T时，函数V的数值解Fig.7 Numerical solution of Vatτ＝T

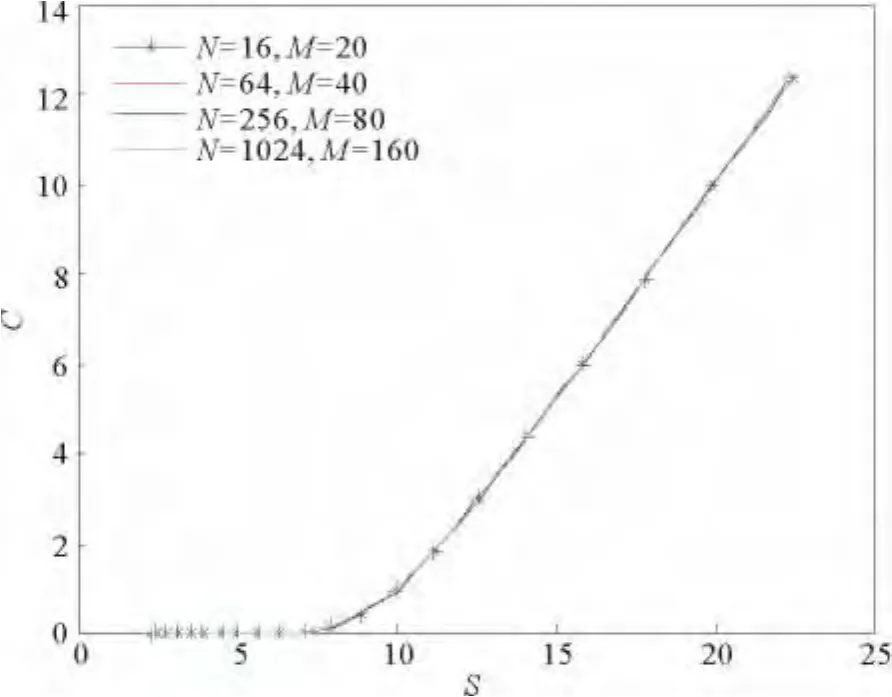
图8 τ＝0时，期权价格C数值解Fig.8 Numerical solution of option price Catτ＝0

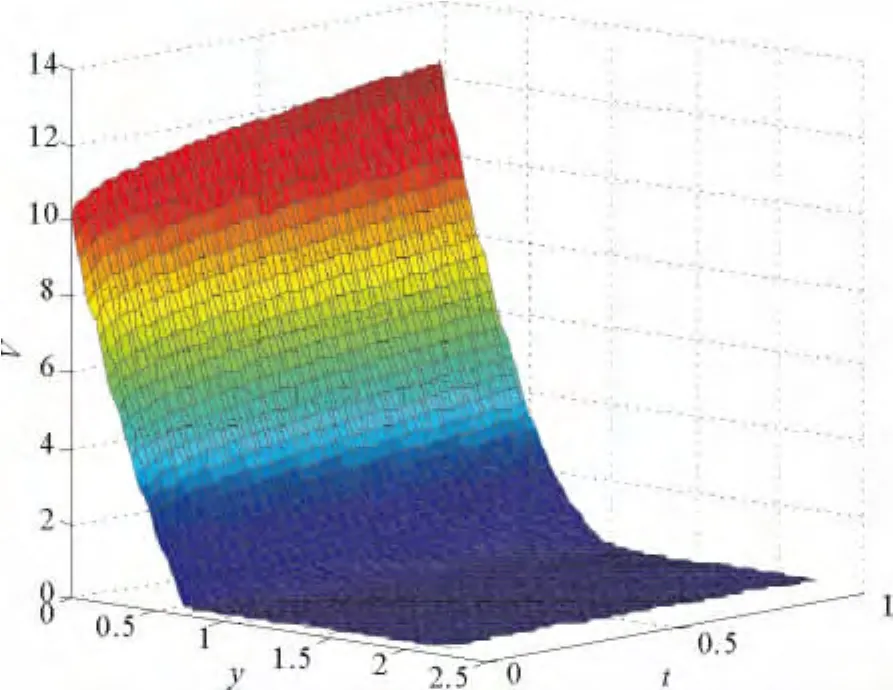
图9 函数V Fig.9 Numerical solution of function V

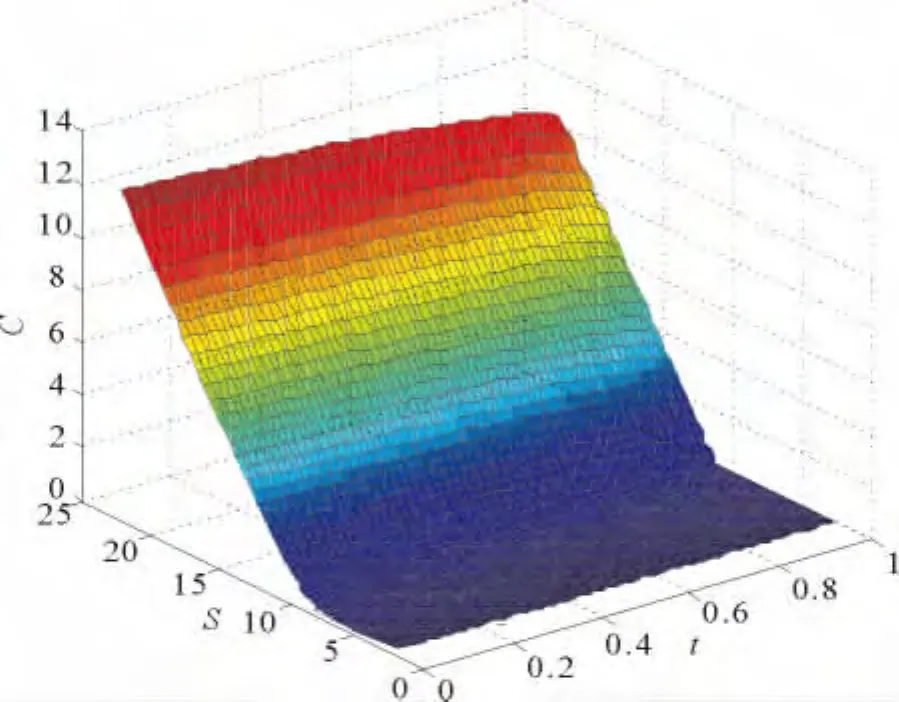
图10 美式买入期权C Fig.10 Numerical solution of American call option C

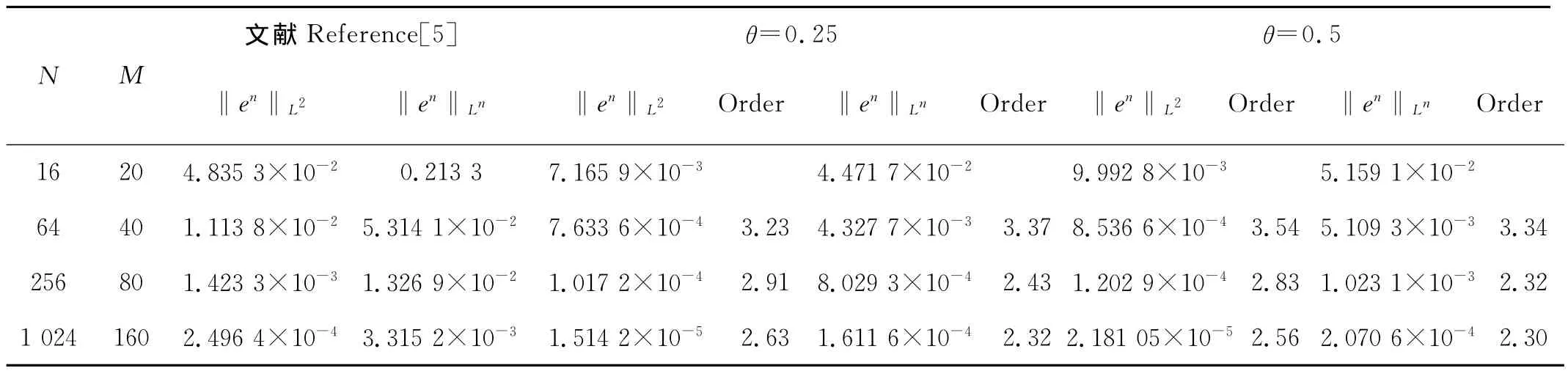
表2 T＝1时，文献［5］差分方法与紧致差分格式取不同θ值的数值结果比较Table 2 Comparison of errors for the scheme in［5］and the compact scheme with differentθat T＝1

表3 紧致差分格式收敛阶Table 3 The rate of the compact difference scheme atτ＝T

4 结语

本文采用Front-fixing方法，对支付红利的美式买入期权模型实施变量替换，将自由边界问题转化为正向的非线性问题，构造3层紧致差分格式求解美式期权定价问题。通过数值实验证明本文方法可以有效计算美式期权问题。

［1］Shreve S E.Stochastic Calculus for FinanceⅠ：The Binomial Asset Pricing Model［M］.New York：Springer，2007.

［2］Holmes A D，Yang H.A front-fixing finite element method for the valuation of American options［J］.SIAM J SCI Comput，2008，30（4）：2158-2180.

［3］Muthuraman K.A moving boundary approach to American option pricing［J］.Journal of Economic Dynamics and Control，2008，32：3520-3537.

［4］Khaliq A Q M，Voss D A，Kazmi K.Adaptiveθ-methods for pri-cing American options［J］.Journal of Computational and Applied Mathematics，2008，222：210-227.

［5］Wu L，Kwok Y.A front-fixing finite difference method for valuation of American options［J］.Journal of financial Engineering，1997，6（2）：83-97.

［6］Wilmott P，Dewynne J，Howison S.Option Pricing：Mathematical Models and Computation［M］.London：Oxford Financial Press，1993.

［7］Kwok Y K.Mathematical Models of Financial Derivatives［M］，New York：Springer，1998.

［8］刘敏.美式期权定价的几种数值解法 ［D］.山东：中国石油大学，2010.