自适应立方卷积图像插值算法

李春龙 潘海侠 王华峰

(北京航空航天大学 软件学院，北京100191)

近年来随着硬件的快速发展，多处理器设备已普及化，且很多设备支持GPU.因此图像数值计算不再是瓶颈问题，用户开始转变为追求高分辨率图像和高清视频.与低分辨率图像相比，高分辨率图像能提供更丰富的细节信息.目前，大量现存的图像获取设备只能获取低分辨率图像，不能满足人们的需要.更换设备耗费巨大，不易实现，且分辨率也不能无限制提高.一种有效的方式是利用图像插值获取高分辨率图像.传统插值算法［1-2］的主要缺陷是不能很好地保持图像边缘，插值后的图像会产生边缘模糊和锯齿.

为了解决插值后图像边缘模糊或锯齿等缺陷，研究人员提出了多种边缘插值算法.Li等人提出一种基于协方差的边缘导向插值算法［3］，从低分辨率图像中估计局部协方差系数，根据高、低分辨率图像局部协方差之间的几何对偶关系实现高分辨率插值.Zhang等人在Li等人的基础上进行改进，提出软判决的插值算法［4］，通过增加局部窗口内像素点之间的约束条件来得到更精确的插值效果.Cvetkovic等人提出一种在小波域中对图像高频分量进行估计的插值算法［5］，虽然这些算法［3-7］都能得到较满意的效果，但运算复杂度较高且占用内存空间较大.为了使算法得到进一步提高，孙毓敏提出结合数据融合技术的插值算法［8］，每个待插值点均融合2个方向上估计值.该算法的插值效果优于双线性算法，但其只能进行2的整数倍的插值.针对传统图像缩放算法边缘处理效果较差，边缘插值算法复杂度较高的问题，本文提出了一种有效增强边缘的自适应立方卷积插值算法.

1 立方卷积算法简介

最邻近插值算法利用待插值点距离最近的像素进行插值，算法简单、运算量小，但没有考虑其他邻域像素的影响.双线性插值算法在水平和垂直方向上进行两次线性插值，与最邻近插值相比，双线性插值考虑了邻域4个点的影响.立方卷积插值算法利用待插值点邻域4个方向上的16个像素点进行插值.该算法不仅考虑到4个直接相邻像素点的影响，而且考虑到各方向像素变化率的影响.插值算法可用公式［9］表示为

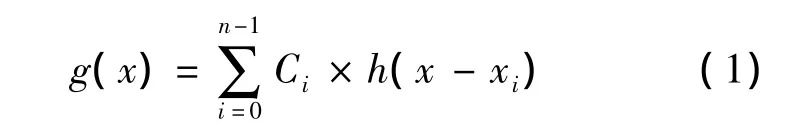
其中，h(x-xi)为插值基函数;Ci为第i个原函数的值.

不同的插值算法只是基函数及选取的插值点个数n不同.大多数三次插值均采用Keys［2］提出的三次插值基函数.

如图1所示 x-1，x0，x1，x2为等间隔的已知像素点，x为待插值点，设h=x1-x0.

Keys［2］的三次插值基函数表达式为

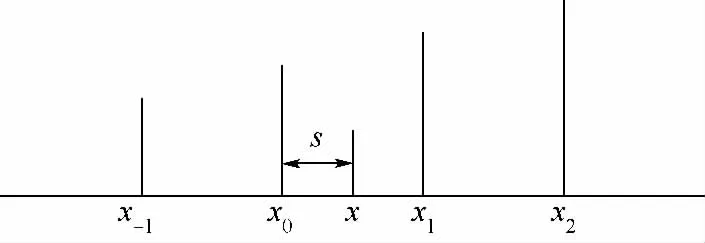
图1 待插值点示意图Fig.1 Diagram of integration point

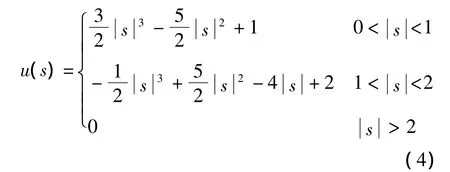
三次运算可以得到更接近高分辨率图像的放大效果，但其没有考虑图像的局部特性.为此，本文提出一种基于边缘检测的自适应立方卷积插值算法:

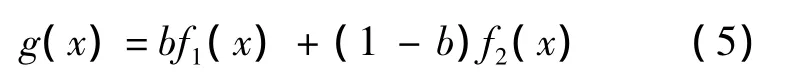
式中，f1(x)为水平方向或45°对角线方向的立方卷积结果;b为权值，在2.2节中将给出权值的计算公式;f2(x)为垂直方向或135°对角线方向的立方卷积结果.

2 自适应立方卷积算法描述

传统插值算法的本质是利用直接邻接点的像素值，或邻接点间像素变化率进行插值.而本文算法首先检测像素点局部特征，根据阈值分为边缘点和非边缘点，然后对两类像素点采用不同的插值策略.具体流程如图2所示.

图2 本文图像插值流程图Fig.2 Flowchart of proposed algorithm

在图2所示的第1步中，选择局部7×7窗口分别沿水平、垂直和两个对角线方向计算像素间差值，与阈值比较.若像素点间差值比预置阈值小，则待插值点归类为非边缘像素点，直接使用立方卷积进行插值;反之，如果像素点间差值比预置阈值大，则待插值点归类为边缘像素点，该类像素点使用本文算法进行插值.

设原图像为 IL，大小为 M×N，将其放大 k倍，放大后图像记为IH，大小为kM×kN.为方便研究，取k=2.

如图3a所示，黑色圆点为原图像像素点，白色圆点、方块点和灰色圆点为放大图像新增像素点，本文插值分两步实现，首先对白色方块点进行插值，插值结果如图3b所示，然后利用第1步结果对白色圆点和灰色圆点进行插值.

图3 插值示意图Fig.3 Diagrams of integration

2.1 边缘检测

为了完成插值，首先进行边缘检测，通常根据梯度变化进行边缘检测.对于模拟图像，其边缘方向是任意的，但对于数字图像，在某一像素的邻域内只有 4 个边缘方向［9-11］，即水平、垂直、45°对角线和135°对角线.

首先以白色方块点为中心点计算梯度，在邻域内4个对角为已知像素点，分别计算45°和135°对角线方向的梯度.如图4所示，在邻域进行梯度计算，则45°对角线梯度计算公式为

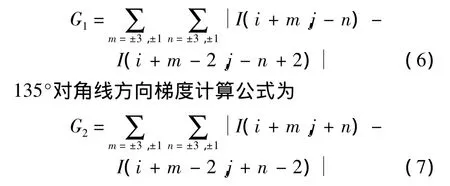
然后以圆点为中心计算梯度，此时方块点为已知，如图5所示，待插值点相邻4像素点为已知点，即水平相邻点和垂直相邻点，且分两种情况;一种情况如图5a水平方向为低分辨率图像实际像素点，垂直方向为第1次已完成插值的点;另一种情况如图5b垂直方向为低分辨率实际像素点，水平方向为第1次已完成插值点.

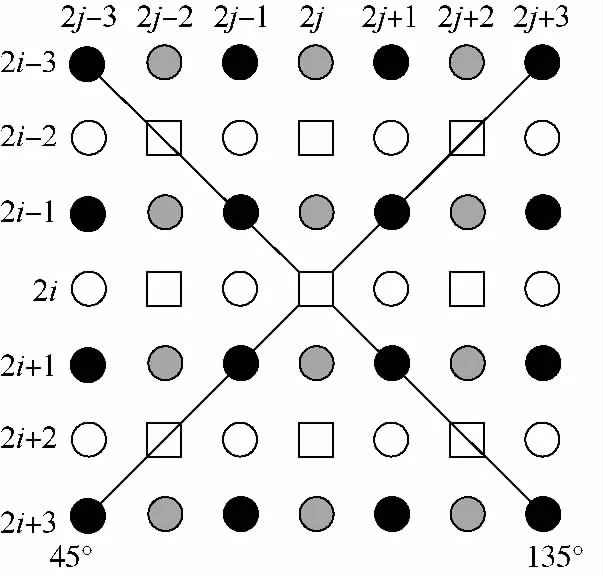
图4 对角线梯度示意图Fig.4 Diagram of diagonal gradient

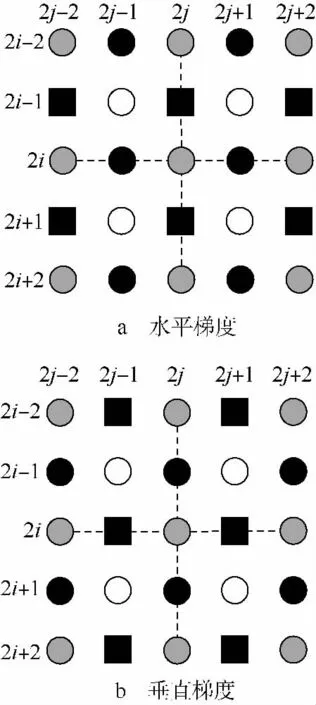
图5 水平与垂直梯度示意图Fig.5 Diagrams of horizontal and vertical gradient

选取5×5邻域进行梯度计算，中心像素点I(x，y)的水平梯度计算公式为

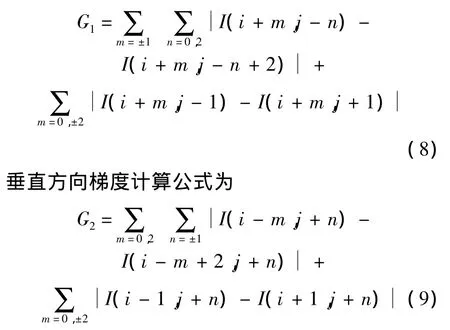
此时，两个正交方向的梯度G1和G2为已知，因此可根据两个梯度的比值(式(10))来确定像素点I(x，y)的强边缘方向.

为防止分母为0，对分子、分母作加1处理，阈值T的选取将在第2.3节进行讨论.

2.2 像素计算

本节讨论如何计算待插值点的像素值.在强边缘方向上缺失的像素点I(x，y)将根据立方卷积算法完成插值.对于弱边缘方向或纹理区域将根据两个正交方向所计算像素加权估计［12-13］.待插值点像素对两正交方向所得像素的相似度与梯度成反比.假设待插值点I(x，y)的两正交方向所得像素分别为p1(45°对角线方向或水平方向)和p2(135°对角线方向或垂直方向)，则p1和p2相结合的权值计算公式为

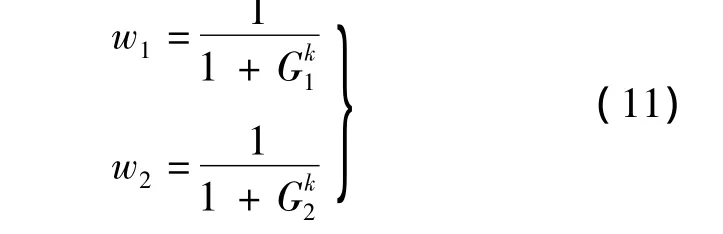
其中k是一个指数参数，用于调整权重的影响，将在第2.3节中讨论k的选取.为防止分母为0作加1处理.在弱边缘方向或纹理区域的待插值点像素计算公式为

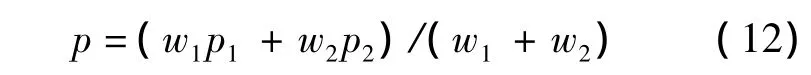
算法描述:

1)初始化:将n×n的低分辨率图像IL放大为(2n-1)×(2n-1)的高分辨率图像IH，两图像对应关系为 IH(2x-1，2y-1)=IL(x，y)，其中 x，y=1，2，…，n.

2)第 1轮插值，对图 3a中的白色方块IH(2x，2y)，x，y=1，2，…，n 进行插值，根据立方卷积计算每一待插值点的45°对角线方向和135°对角线方向的像素p1和p2，根据式(13)确定该点的像素值:

3)第2轮插值，此时方块点为已知像素，对图3b中的灰色圆点IH(2x-1，2y)和白色圆点IH(2x，2y-1)，x，y=1，2，…，n 进行插值，根据立方卷积计算每一待插值点水平方向和垂直方向的像素p1和p2，根据式(13)确定该点的像素值.

2.3 阈值T与指数k的确定

本文算法的关键在于阈值T和指数k的确定，但这两个参数并不能简单地根据所给低分辨率图像计算所得.本文选用24色图像根据机器学习［9］进行计算.首先对样本进行灰度化，并转换为低分辨率图像，然后选取不同的T和k构建高分辨率图像.根据经验值k的选取范围为1～6，步长为1，T的选取范围为1～1.5，步长为0.05.峰值信噪比(PSNR，Peak Signal-to-Noise Ratio)变化趋势如图6所示.

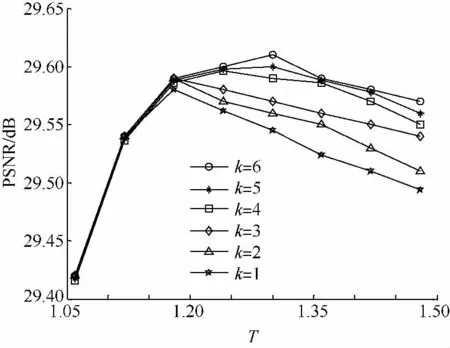
图6 信噪比变化图Fig.6 Curves of PSNR

由图6可知，k=5和k=6的曲线趋于相同，因此增加k并不能进一步提高信噪比，选取k=5.随着T的增加信噪比逐渐增大，但T＞1.25时信噪比开始下降，1.25的T也许是最佳的选择，但是T越大，可能会失去一些强边缘，对比实验结果，本文选择T=1.15.

3 实验结果

针对图像的质量，常用的评价方法［14］有平均平方误差(MSE，Mean Squared Error)、平均绝对误差(MAE，Mean Absolute Error)及 PSNR等.这些方法能较好地反映出图像的质量，但是它们均需要原始图像的参与.图像的平均亮度值(MLV，Mean Luminous Value)直接反映人的主观感受，可以作为其中的一个参考因素.标准差(SD，Standard Deviation)描述了直方图的相对平滑度，熵评价方法(EEM，Entropy Evaluation Method)体现了图像的平均信息量，图像锐利(sharpness)代表了图像的清晰度，高阶统计量(HOS，High Order Statistics)刻画了图像的细节信号对图像质量的贡献.

利用双线性插值、立方卷积，基于边缘特征插值和本文算法进行图像放大，从客观上对放大图像进行质量评估.将琳达和花等原始图像重新取样缩小至1/4，然后分别按双线性插值、立方卷积，基于边缘特征插值和本文算法放大4倍，并与原始图像比较，如图7所示.

图7 各算法插值结果图Fig.7 A set of result images

PSNR值和平均计算时间如表1所示.

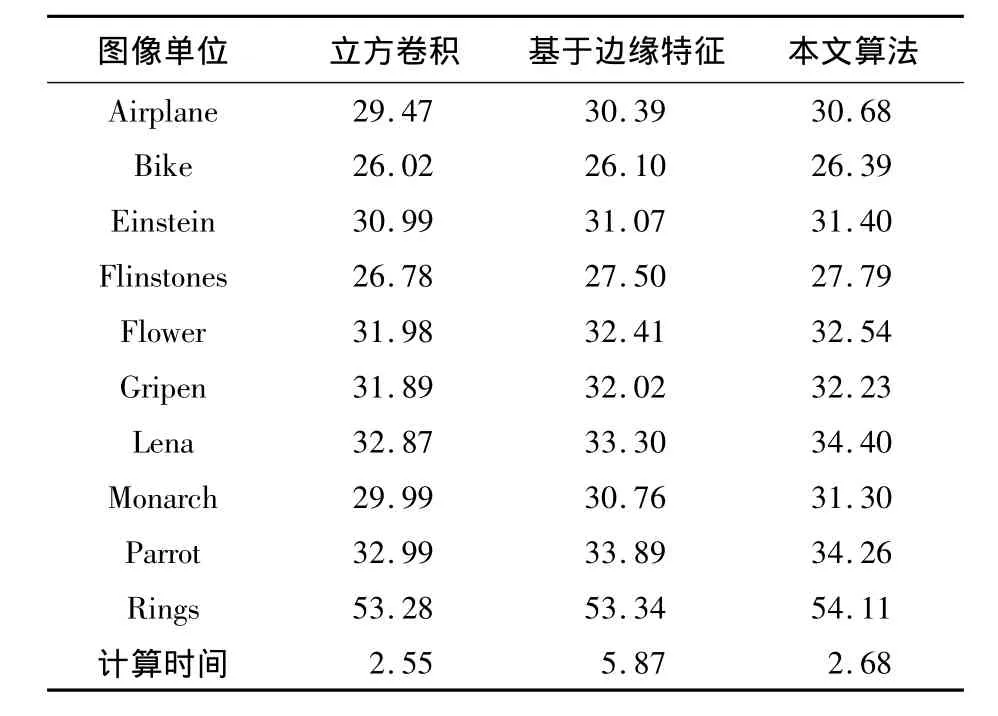
表1 PSNR比较结果和平均计算时间Table 1 PSNR result and average time s

由表1可知，与传统立方卷积插值算法相比，峰值信噪比增加0.89 dB，与基于特征的插值算法相比，平均运行时间降低了3.19 s.

4 结 束 语

使用本文所提的自适应立方卷积插值算法插值后的图像:

1)边缘定向平滑，具有较高的视觉质量，成功消除了传统插值算法存在的边缘锯齿现象;

2)与传统立方卷积插值算法相比，信噪比增加了0.89 dB;

3)与基于特征的插值算法相比，本文所提算法的平均运行时间降低了3.19 s.

References)

［1］ Hou H S，Andrews H C.Cubic splines for image interpolation and digital filtering［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1978，26(6):508-517

［2］ Keys R C.Cubic convolution interpolation for digital image processing［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1981，29(6):1153-1160

［3］ Li X，Orchard M T.New edge-directed interpolation［J］.IEEE Transactions on Image Processing，2001，10(10):1521-1527

［4］ Zhang X J，Wu X L.Image interpolation by adaptive 2-d autoregressive modeling and soft-decision estimation［J］.IEEE Transactions on Image Processing，2008，17(6):887-896

［5］ Chang S G，Cvetkovic Z，Vetterli M.Locally adaptive waveletbased image interpolation［J］.IEEE Transactions on Image Processing，2006，15(7):1471-1485

［6］程光权，成礼智.基于小波的方向自适应图像插值［J］.电子与信息学报，2009，31(3):265-272 Cheng Guangquan，Cheng Lizhi.Direction adaptive image interpolation via wavelet transform［J］.Journal of Electronics＆ Information Technology，2009，31(3):265-272(in Chinese)

［7］ Han J W，Kim J H，Cheon S H，et al.A novel image interpolation method using the bilateral filter［J］.IEEE Transactions on Consumer Electronics，2010，56(1):175-181

［8］孙毓敏.一种基于融合的方向自适应插值算法及其应用［D］.西安:西安电子科技大学，2009 Sun Yumin.A locally orientation-adaptive and fusion-based algorithm for image interpolation［D］.Xi'an:Xidian University，2009(in Chinese)

［9］ Zhou D，Shen X，Dong W.Image zooming using directional cubic convolution interpolation［J］.IET Image Processing，2012，6(6):627-634

［10］杨鹤猛，黄战华.基于梯度的快速图像插值算法［J］.计算机应用，2012，32(10):2821-2826 Yang Hemeng，Huang Zhanhua.Fast image interpolation algorithm based on gradient［J］.Journal of Computer Applications，2012，32(10):2821-2826(in Chinese)

［11］ Feng X J，Allebach J P.Segmented image interpolation using edge direction and texture synthesis［C］//Proceedings of IEEE International Conference on Image Processing.Piscataway，NJ:IEEE，2008:881-884

［12］党向盈，吴锡生，赵勇.基于边缘最大相关性的快速图像插值算法［J］.计算机应用，2006，26(12):2880-2883 Dang Xiangying，Wu Xisheng，Zhao Yong.Fast image interpolation algorithm based on edge-directed max-relativity［J］.Computer Applications，2006，26(12):2880-2883(in Chinese)

［13］ Li M，Nguyen T.Markov random field model-based edge-directed image interpolation［J］.IEEE Transactions on Image Process，2008，17(7):1121-1128

［14］贾小军，喻擎苍，方玫，等.约束点模型的图像放大方法［J］.计算机工程，2008，34(2):232-234 Jia Xiaojun，Yu Qingcang，Fang Mei，et al.Image enlargement method based on constrained points model［J］.Computer Engineering，2008，34(2):232-234(in Chinese)