夹持边界条件下表面裂纹应力强度因子求解

曹淑森 贺小帆 杨博霄 刘文珽

(北京航空航天大学 航空科学与工程学院，北京100191)

航空结构的损伤容限性能主要由含裂纹结构的剩余强度和裂纹扩展性能决定［1］.表面裂纹是飞机结构在使用中可能出现的一种典型裂纹形态，研究表面裂纹的扩展规律、进行裂纹扩展寿命预测对保证飞机结构的使用安全具有十分重要的意义，其中表面裂纹应力强度因子(SIF，Stress Intensity Factor)求解是一个关键的问题［2］.针对有限板的半椭圆形表面裂纹，Newman和Raju利用有限元法给出了拉伸载荷和弯矩作用下应力强度因子的经验公式［3］，Fett估算了任意分布载荷下的表面裂纹应力强度因子［4］，Wang和Lambert等利用权函数法求解了高形状比和低形状比情况下的表面裂纹应力强度因子［5-6］，但这些结果主要针对载荷作用条件，如均匀拉伸、纯弯或线性加载及其线性叠加，没有考虑位移约束.当考虑试件两端固支时，针对表面裂纹应力强度因子，Wang和Lambert等进行了求解［7-8］.

试验是研究表面裂纹扩展的重要手段，通常需要在试验室进行模拟试件的表面裂纹扩展试验，这种条件下有限尺寸的试件往往直接夹持在试验机上，其边界条件为复杂的载荷和位移边界条件，已有的载荷或位移边界条件下的应力强度因子解不适用，必须模拟实际夹持边界条件寻求应力强度因子解.John和Rigling分析了夹持边界条件对矩形板单边穿透裂纹的应力强度因子的影响［9］.John等利用权函数法求解了夹持边界条件下单边穿透裂纹的应力强度因子［10］.针对夹持边界条件下单边裂纹的应力强度因子，Blatt等利用柔度法和有限元法进行了分析［11］，Jones利用权函数法进行了求解［12］.但是针对试验机夹持边界条件下表面裂纹的应力强度因子的求解还鲜有报道.为此，本文拟针对试验室表面裂纹扩展试验这一问题，进行夹持边界条件下的应力强度因子求解，并与有限元计算结果进行对比，在此基础上，讨论了试件几何和裂纹尺寸对应力强度因子的影响.

1 等效模型的建立

1.1 试验机夹持边界条件分析

典型的疲劳试验示意图见图1.特点如下:①与试件相比，夹具的几何尺寸很大，可近似为刚性体;②由于机架的约束，作动筒只能沿轴向运动.与自由均匀拉伸加载条件相比，刚性夹具的轴向运动对试件端部造成位移和转角约束，试件端部只能沿轴向方向运动且转角为0°.

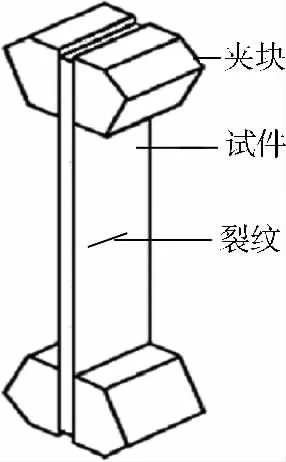
图1 疲劳试验夹持条件Fig.1 Clamped ends condition in fatigue tests

1.2 等效模型

由于夹持边界条件非常复杂，直接对夹持边界条件下表面裂纹应力强度因子进行求解难以实现，虽然有限元方法(FEM)是一种有效的工具，但是计算量太大，并不实用.为此，本文对夹持边界条件进行等效简化，示意图见图2.在夹持条件下，试件除了受到沿轴向的载荷外，由于端部的自由度受到约束，等效为在端部施加了一个yz平面内的弯矩，方向如图2中所示，弯矩使试件端部的转角为0°.从而夹持边界条件可等效为均匀拉力和弯矩作用，两者的共同作用使试件端部的转角为0°.

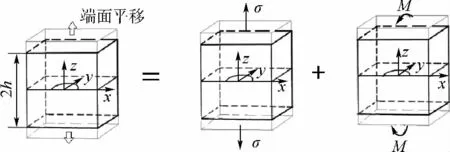
图2 等效模型建立Fig.2 Establishment of the equivalent model

2 基于等效模型的应力强度因子求解

2.1 应力强度因子叠加

在线弹性条件下，应力强度因子等于各载荷作用下应力强度因子之和.显然，一旦均匀拉伸和弯矩作用下的应力强度因子解已知，即可由式(1)得到均匀拉伸和弯矩共同作用下的应力强度因子.

式中，Kσ为均匀拉伸作用下应力强度因子;KM为弯矩作用下应力强度因子.

2.2 均匀拉伸和弯矩作用下应力强度因子解

Newman-Raju公式［2］给出了在均匀拉伸应力和弯矩共同作用下表面裂纹在全范围内应力强度因子解，见下式:

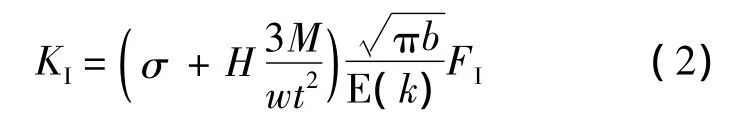
其中，2w为试件宽度;t为试件厚度;b为裂纹深度;E(k)为第二类完全椭圆积分;FI为形状系数;H为与裂纹形状相关的系数［2］.试件几何及裂纹尺寸定义见图3，其中2a为裂纹长轴.

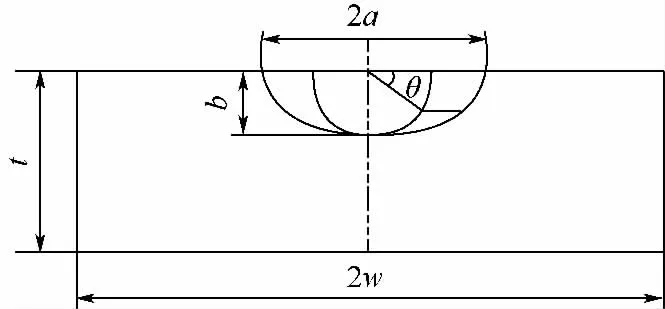
图3 含裂纹截面示意图Fig.3 Schematic diagram of the intersecting surface including the crack

2.3 等效弯矩求解

在试验条件下，试件所受的拉力是已知的，但等效弯矩是未知的.当拉力越大时，端部产生的转角也越大，使端部转角恢复为0的弯矩也越大，反之亦然.所以等效弯矩由拉力大小决定，两者成函数关系.

根据I型裂纹应力强度因子与能量释放率之间的关系可知能量释放率为

式中，G为能量释放率;平面应力状态时E'=E，平面应变状态E'=E/(1-ν2)，其中E为弹性模量，ν为泊松比.

弹性位能Π和能量释放率G之间有如下关系:

式(7)积分与裂纹扩展路径无关［7］，受拉伸载荷和弯曲疲劳载荷下表面裂纹形状近似为椭圆形［14］，为了求解方便，假定在裂纹扩展中，裂纹前缘成比例扩展［15］，裂纹在扩展后仍然为椭圆形，如图4所示.

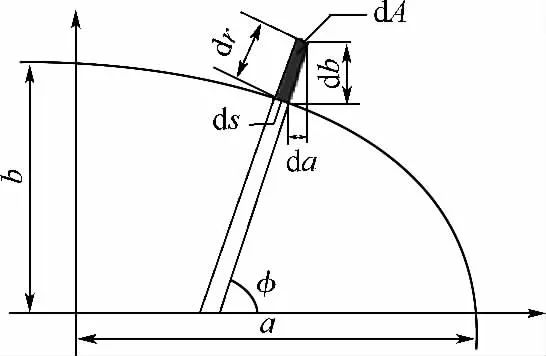
图4 裂纹等比扩展Fig.4 Crack growth in proportion

从而有

其中df为比例常数.根据投影原理，从图4可见，法向位移dr和弧长ds为

考虑到表面裂纹前缘随着角度的变化应力状态不同，所以沿着裂纹前缘E'值是变化的，在沿表面方向(θ=0°)是平面应力状态，E'=E;沿深度方向(θ=90°)是平面应变状态，E'=E/(1-ν2).参考文献［12］取

2.4 基于等效模型的应力强度因子

将式(17)代入式(1)可得夹持条件下表面裂纹应力强度因子为

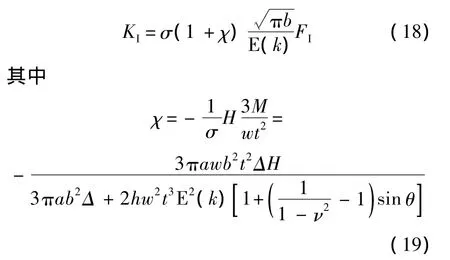
显然，夹持边界条件下的表面裂纹应力强度因子是在Newman-Raju公式的基础上乘上参数1+χ.夹持边界条件下表面裂纹应力强度因子可由自由均匀拉伸条件下的应力强度因子得到，即

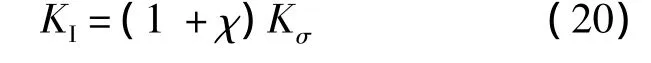
3 等效模型的有限元验证

3.1 有限元验证的目的

在选取E'时采用了文献［15］给出的近似公式，等效模型是否能很好地符合夹持边界条件，能否反映真实的应力应变状态有待验证.

由于上述问题的存在，等效模型的合理性需要验证.有限元方法是一种精度很高的数值方法，因此本文采用Abaqus软件对等效模型进行验证.Abaqus采用三维J积分法计算应力强度因子，计算精度较高［16］.

3.2 有限元建模

建立自由拉伸条件下的有限元模型如图5所示，材料弹性模量为210 GPa，泊松比为0.3.在试验条件下，夹块夹持试件，拉伸载荷施加在夹块上，通过夹块传递给试件.采用刚体来代替试验机的夹块以模拟夹持边界条件，如图6所示.刚体与夹块夹持部位相同;同时约束刚体的横向位移和转动，使之只能沿着载荷施加的方向移动.在刚体的约束下，试件端部只能沿载荷施加方向移动，这样试件与真实试验机夹持条件下的位移边界条件基本一致.

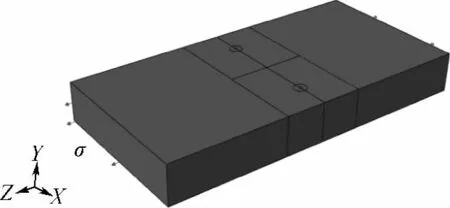
图5 自由拉伸条件下试件模型Fig.5 Specimen model unde free uniform tension

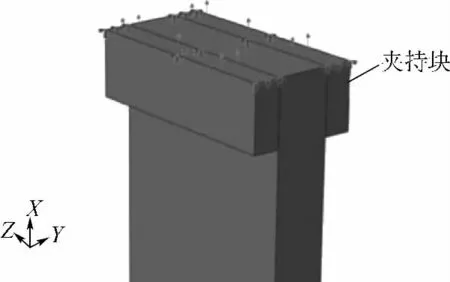
图6 夹持条件的建模Fig.6 Model of the clamped ends conditions

网格划分如图7和图8所示.划分网格时，在裂纹前缘处分为3个部分，如8中区域1，2，3所示.区域1为裂纹前缘所在区域，以裂纹前缘为轴线，横截面沿圆周设置24个种子，沿裂纹前缘设置60个种子，网格形状为楔形，类型为C3D6，网格划分方法采用扫掠;区域2以裂纹前缘为轴线，横截面沿圆周设置24个种子，沿径向设置4个种子，单向等比扩展，最大与最小的比值为2，沿裂纹前缘方向设置60个种子，网格形状为六面体，类型为C3D8R，网格划分方法为扫掠;过渡区域(区域3)采用自由网格划分，网格类型为四面体网格C3D4;剩余部分采用六面体单元C3D8R，自由网格划分.

图7 整体网格划分图Fig.7 Mesh method of the whole model

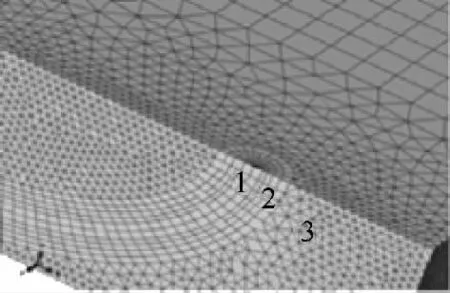
图8 含裂纹处网格划分Fig.8 Mesh mehtod of the part including crack

3.3 夹持边界条件对表面方向和深度方向应力强度因子的影响

对于表面裂纹，裂纹前缘的应力强度因子随着角度不同而不同，在裂纹前缘为半椭圆形的假设下θ=0°和θ=90°的应力强度因子最受关注.式(18)计算夹持条件和均匀拉伸条件下的应力强度因子，结果见表1.结果表明夹持条件对SIF的影响在θ=0°时非常明显，而在θ=90°时则很小.利用有限元法进行计算，结果如图9所示，可以得到同样的结论.因此为了减少计算量，在下一步的讨论中，只研究夹持条件对θ=0°时应力强度因子的影响，来检验本文提出的应力强度因子解的合理性.

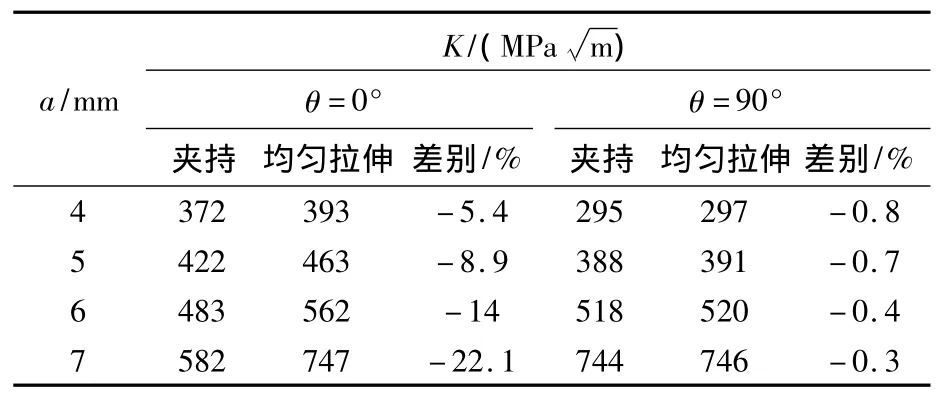
表1 夹持条件与均匀拉伸条件下的应力强度因子KTable 1 Comparison of SIFs under free uniform tension and clamped ends condition

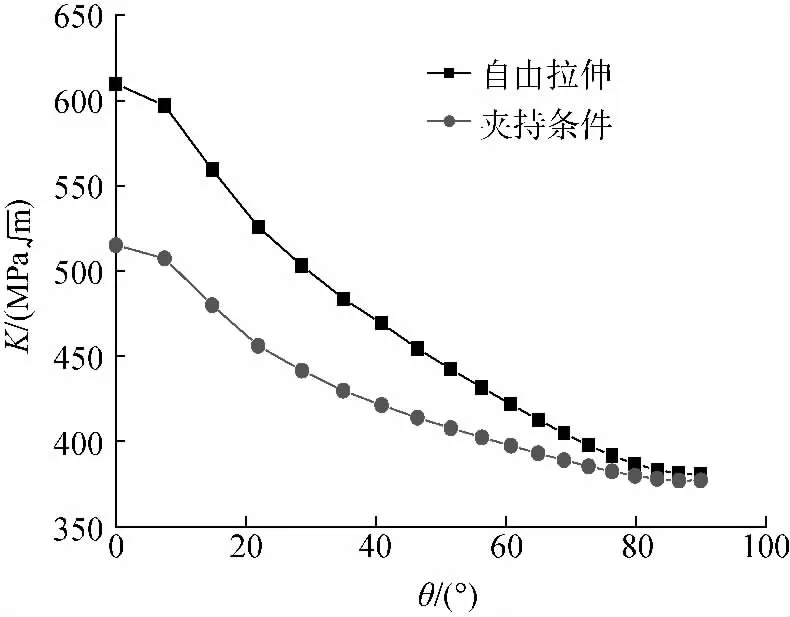
图9 自由拉伸和夹持条件下K-θ曲线(h=20 mm，w=7.5 mm，t=5 mm，a=6 mm，b=4 mm)Fig.9 K-θ curves under free uniform tension and clamped ends condition(h=20 mm，w=7.5 mm，t=5 mm，a=6 mm，b=4 mm)

3.4 夹持边界条件下应力强度因子解的检验

由式(19)可知，试件及裂纹的尺寸都是影响修正因子1+χ的重要参数.为了检验1+χ是否能正确反映应力强度因子的影响，需要检验不同试件及裂纹尺寸下的1+χ的准确性.选取典型尺寸的含表面裂纹试件，利用式(19)求出对应的1+χ值，然后分别建立自由拉伸条件下和夹持边界条件下的有限元模型，求解应力强度因子，得到1+χ;比较两种方法求得的1+χ值，即可检验基于等效模型的应力强度因子公式是否正确.

取试件的尺寸不变，裂纹深度b不变，分别用式(19)和Abaqus软件求解1+χ，计算结果见图10a;取裂纹尺寸不变，改变试件长度h，求解1+χ，计算结果见图10b、图10c.

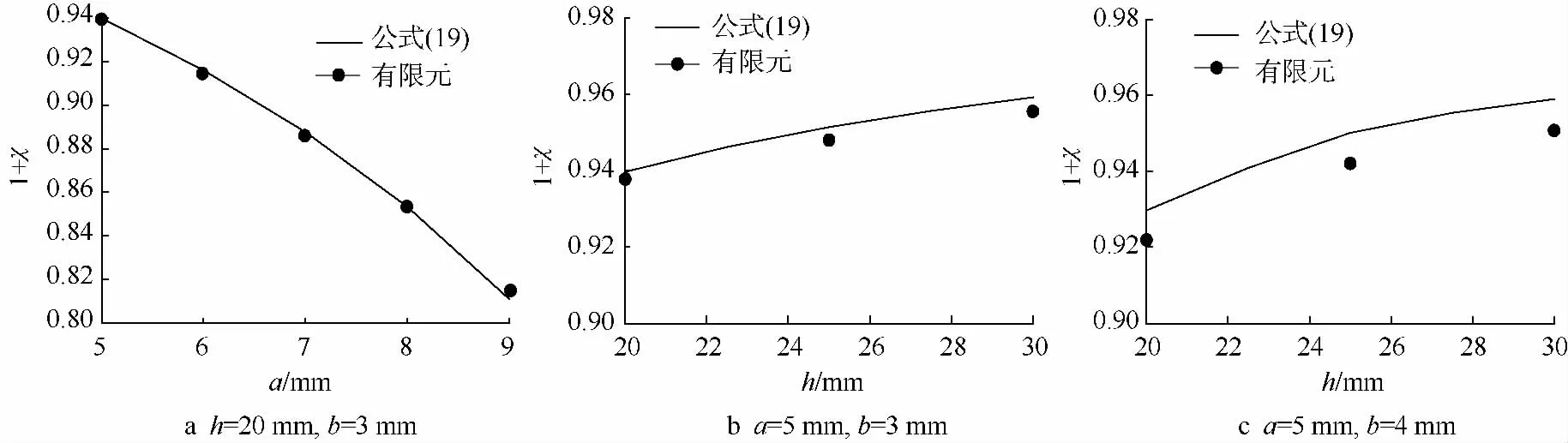
图10 公式(19)与有限元计算所得修正因子结果比较(w=10 mm，t=5 mm，θ=0°)Fig.10 Comparison of the correction factor from equation solutions and finite element solutions(w=10 mm，t=5 mm，θ=0°)

计算结果表明，随着表面裂纹宽度的改变，利用式(19)和有限元法计算的1+χ值差别很小;随着裂纹深度的改变和试件长度的改变，两种方法所求得的1+χ差别均小于2%.

显然，式(19)的精度是满足要求的.

4 影响因素分析

夹持边界条件对表面裂纹应力强度因子的影响反映在参数1+χ上，影响1+χ的因素包括试件长度、宽度、厚度，裂纹尺寸等.为了研究夹持边界条件对不同裂纹及试件尺寸时裂纹应力强度因子的影响，需要分别研究各个参数对1+χ的影响.各种因素的变化对1+χ的影响见图11.

结果表明:a/w和b/t越大，即裂纹尺寸越大，修正因子越小;h/t越大，即试件的尺寸越大，修正因子越大;b/a越大，修正因子越大.

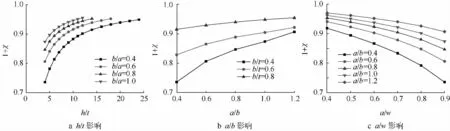
图11 不同参数对修正因子的影响Fig.11 Curves of correction factor under deferent variables

5 结论

1)建立了夹持边界条件下表面裂纹应力强度因子求解的等效模型，即将夹持条件等效为均匀拉伸与弯矩的共同作用，并且试件端部转角为0°，给出了等效弯矩和均匀拉伸应力的关系，采用叠加原理给出了夹持边界条件下应力强度因子解，其形式为自由均匀拉伸载荷作用应力强度因子解乘以一个与试件和裂纹尺寸有关的修正因子;

2)与Abaqus有限元数值解的计算对比表明，基于该等效模型的夹持边界条件下的应力强度因子解是合理的;

3)分析了试件几何和裂纹尺寸对修正因子的影响，当裂纹尺寸较大或者试件长厚比(h/t)较小时，夹持条件会对沿宽度方向的应力强度因子产生比较明显的影响.

References)

［1］郭万林，于培师.构件三维断裂与疲劳力学及其在航空工程中的应用［J］.固体力学学报，2010(5):553-571 Guo Wanlin，Yu Peishi.Three dimensional fracture and fatigue mechanics of structures and its application in aeronautical engineering［J］.Chinese Journal of Aeronautics，2010(5):553-571(in Chinese)

［2］郭万林.复杂环境下的三维疲劳断裂［J］.航空学报，2002，23(3):215-220 Guo Wanlin.Three dimensional fatigue fracture in complex environment［J］.Acta Aeronautica et Astronautica Sinica，2002，23(3):215-220(in Chinese)

［3］ Newman Jr J C，Raju I S.An empirical stress-intensity factor equation for the surface crack［J］.Engineering Fracture Mechanics，1981，15(1):185-192

［4］ Fett T.Estimation of stress intensity factors for semi-elliptical surface cracks［J］.Engineering Fracture Mechanics，2000，66(4):349-356

［5］ Wang X，Lambert S B.Stress intensity factors for low aspect ratio semi-elliptical surface cracks in finite-thickness plates subjected to nonuniform stresses［J］.Engineering Fracture Mechanics，1995，51(4):517-532

［6］ Wang X，Lambert S B.Stress intensity factors and weight functions for high aspect ratio semi-elliptical surface cracks in finitethickness plates［J］.Engineering Fracture Mechanics，1997，57(1):13-24

［7］ Wang X，Lambert S B.Semi-elliptical surface cracks in finitethickness plates with built-in ends.I.Stress intensity factor solutions［J］.Engineering Fracture Mechanics，2001，68(16):1723-1741

［8］ Wang X，Lambert S B.Semi-elliptical surface cracks in finitethickness plates with built-in ends.II.Weight function solutions［J］.Engineering Fracture Mechanics，2001，68(16):1743-1754

［9］ John R，Rigling B.Effect of height to width ratio on K and CMOD solutions for a single edge cracked geometry with clamped ends［J］.Engineering Fracture Mechanics，1998，60(2):147-156

［10］ John R，Kaldon S G，Johnson D A，et al.Weight function for a single edge cracked geometry with clamped ends［J］.International Journal of Fracture，1985，72(2):145-158

［11］ Blatt D，John R，Coker D.Stress intensity factor and compliance solutions for a single edge notched specimen with clamped ends［J］.Engineering Fracture Mechanics，1994，47(4):521-532

［12］ Jones I S.A wide range weight function for a single edge cracked geometry with clamped ends［J］.Ineternational Journal of Fracture，1998，89(1):1-18

［13］单辉祖.材料力学(II)［M］.3版.北京:高等教育出版社，2009:35-71 Shan Huizu.Mechanics of materials(II)［M］.3rd ed.Beijng:Higher Education Press，2009:35-71(in Chinese)

［14］吴志学.表面裂纹疲劳扩展的数值模拟(II)［J］.应用力学学报，2007，24(1):42-46 Wu Zhixue.Numercal simulation to surface crack fatigue growth(II)［J］.Chinese Journal of Applied Mechanics，2007，24(1):42-46(in Chinese)

［15］张行.断裂力学［M］.北京:宇航出版社，1990:164-169 Zhang Xing.Fracture mechanics［M］.Beijing:Aerospace Press，1990:164-169(in Chinese)

［16］林晓斌，Smith R A.应用三维有限单元法计算应力强度因子［J］.中国机械工程，1998，9(11):39-42 Lin Xiaobin，Smith R A.Calculation of stress intensity factors using the 3D finite element method［J］.China Mechanical Engineering，1998，9(11):39-42(in Chinese)