复合材料开孔层压板压缩长期强度预测

康 军 关志东 黎增山 李 星

(北京航空航天大学 航空科学与工程学院，北京100191)

复合材料具有比强度、比刚度高及可设计性等特点，已广泛应用于航空航天结构中，在长期使用过程中的强度预测越来越受到关注.众所周知，聚合物复合材料的性能不仅是时间的函数，还与温度相关，具有时间-温度相关性，即黏弹性［1］.因此，可以利用时间-温度叠加原理，通过提高试验温度来加快试验速度.

加速试验方法(ATM，Accelerated Testing Methodology)基于时间-温度叠加原理，将不同温度、加载速率下的强度-时间曲线段沿时间轴平移，构成参考温度下的强度-时间曲线.Miyano等人［2］研究了碳纤维复合材料的静载强度、蠕变强度和疲劳强度的时间温度相关性，提出了复合材料强度预测加速试验方法.Miyano［3-5］，Nakada［6-7］，Cai［8］，Iwai［9］等人进行了复合材料层压板拉伸、压缩、弯曲、机械连接，以及湿热环境下的静载、蠕变和疲劳试验，验证了加速试验方法的适用性.

应变不变量失效理论(SIFT，Strain Invariant Failure Theory)由 Goose和 Christensen 提出［10］，是一种基于物理失效模式的强度理论，将基体的失效模式分为膨胀失效和扭曲失效.通过代表体积单元将“宏观”应变放大，分析纤维与基体间的相互作用，同时考虑了固化残余应力的影响.Tay和 Sun［11-12］等人用渐进损伤分析方法，将SIFT和单元失效法(EFM，Element Failure Method)相结合，用于预测开孔层压板拉伸载荷下失效过程.

Tsai等人［13］结合应变不变量理论和加速试验方法(SIFT/ATM)，采用经典层压板理论进行宏观应力分析，预测复合材料层压板在不同温度及湿度环境下的疲劳失效寿命，并将该方法在Microsoft Excel中开发了疲劳寿命和剩余强度软件Super Mic-Mac.由于应力分析采用了经典层压板理论，该方法无法分析带应力集中的复合材料结构，如开孔、加筋板、连接件的强度与寿命.Cai等人［14-15］采用三维有限元模型进行宏观应力分析，基于SIFT/ATM方法预测准各向同性开孔层压板匀速加载下长期压缩强度.但是Cai采用孔边单元失效作为开孔板最终失效准则，并未对开孔层压板的失效过程进行分析.

本文对应变不变量失效理论中纤维失效准则进行改进，并结合加速试验方法和渐进损伤分析，模拟了开孔层压板压缩失效过程，分析了纤维和基体失效，预测了复合材料开孔层压板匀速加载下长期压缩强度.计算结果与试验结果吻合很好，证明了该方法的适用性.

1 加速试验方法

黏弹性树脂具有时间-温度相关性的特点，符合时间-温度叠加原理(TTSP，Time-Temperature Superposition Principle)，因此可通过提高试验温度加速试验进程.ATM利用TTSP预测复合材料的长期强度.

Miyano等人［2］在大量试验的基础上，提出加速试验方法.ATM预测复合材料长期强度基于以下假设:

假设A 静载、蠕变、疲劳强度服从相同的时间-温度叠加原理，即3种强度的平移因子相同;

假设B 单调载荷损伤服从线性累积损伤;

假设C 疲劳强度与应力比为线性关系.

根据假设 A，静载强度(CSR，Constant Strain Rate)控制曲线由不同温度下，相同加载速率的试验曲线连接构成;应力比为零的疲劳强度控制曲线由不同温度、相同加载频率的疲劳强度试验曲线段构成.根据假设B，CSR强度控制曲线导出蠕变强度控制曲线.根据假设C，任意应力比的疲劳强度可由蠕变强度控制曲线(R=1)和疲劳强度控制曲线(R=0)插值得到.

加速试验方法的应用流程如图1所示.

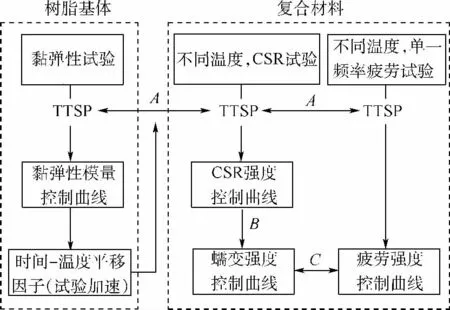
图1 加速试验方法应用流程Fig.1 Procedure of accelerated testing methodology

2 应变不变量失效理论(SIFT)

2.1 纤维和基体失效准则

复合材料由纤维和基体组成，应变不变量失效理论将纤维和基体失效分为膨胀失效和扭曲失效，分别采用材料第一应变不变量 J1和 Von Mises应变来判断.

通过对纤维失效机理分析，本文对纤维失效准则进行了改进.由于纤维为脆性材料，其破坏垂直于纤维方向发生，纤维轴向的应变起主要作用，采用最大应变准则判断失效.

1)纤维拉伸失效:

2)纤维压缩失效:

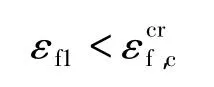
基体由于存在微裂纹，其失效包线在第1象限有截断.基于该象限 Goose等人［10］提出 SIFT，把基体失效分为膨胀失效和扭曲失效，分别采用材料第一应变不变量 J1和 Von Mises应变来判断.

1)基体膨胀失效:

2)基体扭曲失效:

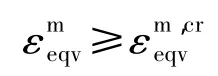
2.2 宏观应变和细观应变关系

应变不变量理论建立在纤维和基体细观应变分析上，需根据宏观应变通过应变放大系数转换得到纤维和基体的细观应变.应变放大系数通过纤维和基体的代表体积单元模型(RVE，Representative Volume Element)分析得到.RVE是基于纤维和基体的典型分布建立的细观模型，用以研究纤维和基体的相互作用.本文采用的RVE分为正方形和六边形，如图2所示.两种模型中在纤维和基体上取出20个具有代表性的位置作为参考点.参考点选取如图2所示，其中11个在基体，9个在纤维.通过对RVE分别在3个方向施加单位正应变、剪切应变和温度载荷，可以得到纤维和树脂在参考点位置的应变，从而计算出相应位置的应变放大系数.

图2 RVE及参考点选取Fig.2 RVE and reference points chosen

复合材料结构单层细观应变和宏观应变之间的关系如下:

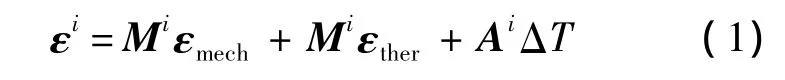
其中，εi为位置i处的纤维或者树脂三维微观应变;εmech为机械载荷作用下的单层三维宏观应变;εther为热载荷作用下的单层三维宏观应变;Mi为位置i处的机械应变放大系数矩阵;Ai为位置i处由于纤维和树脂热不匹配性引起的热应变放大系数向量;ΔT为固化温度和使用温度之间的温差.

2.3 失效模式与失效准则

宏观应变通过应变放大系数得到参考点处的细观应变，根据应变不变量失效准则分别对每个参考点进行失效判断.由于20个参考点分别位于基体、纤维上，不同位置采用不同的失效准则.失效模式及判断准则如表1所示.

表1 失效模式及判断准则Table 1 Failure modes and damage determination

正交各向异性材料的应力应变关系如下:

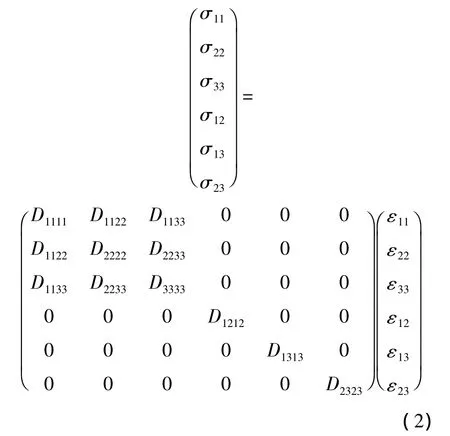
纤维和基体发生损伤时，对刚度矩阵中的相关元素进行折减.刚度矩阵衰减如表2所示.

表2 刚度矩阵衰减Table 2 Stiffness matrix degradation

3 SIFT/ATM方法流程

SIFT/ATM方法预测复合材料结构长期强度如图3所示，具体过程如下:

1)树脂基体在不同温度下DMA(Dynamic Mechanical Analysis)试验，得到基体模量的控制曲线和时间温度平移因子;

2)在不同温度下，测量复合材料单层板的纵向、横向的拉伸和压缩破坏应变，并利用基体的平移因子对不同温度下的破坏应变平移，得到单层板的破坏应变控制曲线;

3)建立试验的单层板有限元模型，加载为试验测得的应变，采用SIFT，计算两种RVE参考点处的等效应变，纤维和基体的SIFT临界值为失效模式对应参考点上SIFT参数的最大值，失效模式定义如表1所示;

图3 SIFT/ATM预测复合材料长期强度Fig.3 Prediction of long-term strength of composite materials with SIFT/ATM

4)对复合材料结构宏观应变分析和细观应变分析，根据SIFT临界值控制曲线和失效判据对复合材料结构进行失效分析，材料失效后对刚度矩阵进行相应衰减，如表2所示，得到对应失效时间的强度.

4 开孔层压板压缩长期强度预测

4.1 加速试验

本文计算所采用的试验数据来自文献［15］，材料为TR30S/epoxy.加速试验内容包括树脂基体、单向层压板和铺层为［45/0/45/90］3s的准各向同性开孔层压板，如表3所示.

表3 加速试验矩阵［15］Table 3 Accelerated test matrix［15］

树脂基体在不同温度和频率下DMA得到树脂基体的储能模量控制曲线和时间温度平移因子;单向层压板在不同温度下，纵向、横向进行拉伸和压缩静载试验得到单向层压板纵向、横向的拉伸和压缩失效应变控制曲线，并通过 SIFT/ATM计算得到纤维和基体的SIFT临界值的控制曲线;开孔层压板不同温度下静载压缩试验得到开孔层压板的压缩强度控制曲线，与预测结果进行比较.开孔压缩试验件尺寸如图4所示，层压板纤维体积含量为0.6.

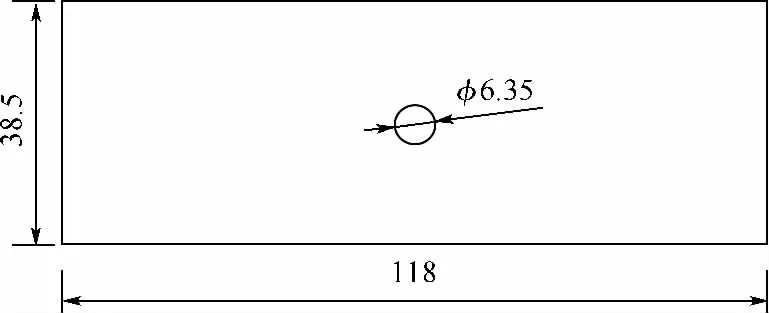
图4 开孔层压板尺寸Fig.4 Specimen size of open-hole compressive(OHC)laminates

4.2 基体储能模量控制曲线和时间温度平移因子

树脂基体在不同温度和频率下进行动态力学试验，得到不同温度下的模量-加载时间(E-t)曲线.加载时间t与加载频率f有如下关系:

以T0=25℃为参考温度，将不同温度下的E-t曲线水平平移，构成光滑的模量-还原时间(E-t')曲线，该曲线为基体储能模量控制曲线.水平方向平移的量定义为该试验温度相对于参考温度T0的时间温度平移因子αT0(T)，可采用两个活化能ΔH1和ΔH2分段表示的Arrhenius方程:

式中G=8.314×10-3kJ/(K·mol)为气体常数.

图5为树脂基体的时间温度平移因子曲线.

图5 时间温度平移因子［15］Fig.5 Time-temperature shift factors［15］

基体DMA试验得到的时间温度平移因子用于计算单层板失效还原时间，构成单向板破坏应变控制曲线和纤维、基体SIFT临界值控制曲线.表达式为

式中，ts为温度T时的层压板失效时间，t's为参考温度T0下的还原时间.

4.3 应变不变量临界值控制曲线

单向层压板在不同温度下进行纵向、横向拉伸和压缩试验得到应力-应变曲线、破坏应变以及试验静载失效时间ts.取T=25℃的储能模量作为基体的杨氏模量，并利用RVE模型反推出常温下纤维的模量和热膨胀系数，如表4所示.

将各组破坏应变按照时间温度平移因子αT0(T)沿水平方向平移，得到纵向、横向拉伸和压缩破坏应变控制曲线，见文献［15］.

构造SIFT临界值的控制曲线可通过对时间进行分割，求得ti时刻的SIFT临界值，并将不同时刻的SIFT临界值连接.ti时刻SIFT临界值的计算过程如下:

1)取树脂基体储能模量控制曲线上ti时刻的模量E(ti)作为两种RVE的基体模量，并计算出两种RVE的应变放大矩阵;

2)建立单向板模型，载荷为单向层压板破坏>应变控制曲线ti时刻的破坏应变;

3)通过宏观应变和微观应变转换公式(1)，得到纤维和基体的微观应变，纤维和基体的SIFT临界值取两种RVE中等效应变的最大值.

表4 TR30S/epoxy纤维和基体性能(T=25℃)Table 4 Fiber and matrix properties of TR30S/epoxy(T=25℃)

图6为TR30S/epoxy的SIFT临界值控制曲线.从图中可以看到，纤维拉伸失效的临界值随着t's的增加变化很小，纤维的拉伸性能受时间的影响很小;纤维的压缩失效临界值随着t's的增加显著下降;基体膨胀失效的临界值随着t's的增加而下降，可见基体的膨胀失效受时间影响明显;但基体扭曲失效的临界值却随着t's的增加而明显上升，这是因为基体的弹性模量 E(t's)，泊松比ν(t's)和体积模量K有如下关系:

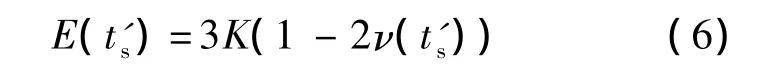
其中，体积模量K为材料常数，随着t's和温度的增加，基体弹性模量E(t's)下降，泊松比ν(t's)却由0.35增大到接近0.5，导致基体更容易产生形状扭曲.

4.4 长期强度预测算例

为了验证SIFT/ATM方法所得到的材料应变不变量临界值控制曲线，对复合材料开孔层压板在静载压缩载荷下长期强度预测和失效过程分析，并与试验结果进行对比.

试验件尺寸见图4，铺层为［45/0/45/90］3s.有限元模型见图7，采用三维实体线性减缩积分单元C3D8R，并采用变密度网格，在孔周围用较密的网格以模拟损伤的过程，单元总数为31678.为了防止开孔压缩实验过程中试件失稳，采用开孔压缩夹具.有限元模型模拟了压缩过程中夹具对试件约束作用，边界条件为一端固支，另一端施加位移载荷，试件表面孔边25.4mm×16.2mm矩形区域未施加面外位移约束(图7孔边深色区)，其他位置约束面外位移.

图8为T=25℃时，开孔压缩层压板损伤起始失效模式，为便于显示，图中仅显示了孔边区域.层压板在初始损伤时，45°和90°层主要是孔边的基体膨胀失效和基体剪扭曲失效，0°层孔边有少量的纤维压缩失效，同时基体也产生了基体膨胀和扭曲失效;各单层的损伤沿-45°方向扩展，最终整体破坏.

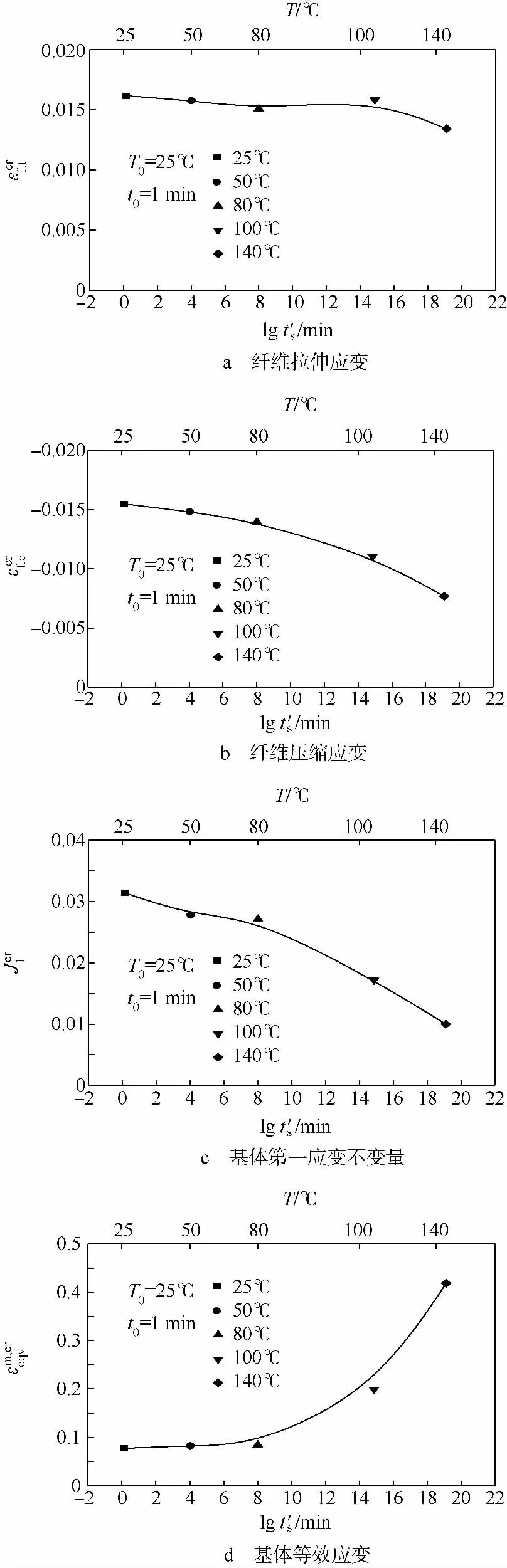
图6 TR30S/epoxy的SIFT临界值控制曲线Fig.6 Master curves of SIFT critical parameters for TR30S/epoxy

图7 开孔压缩有限元模型Fig.7 FE model of OHC laminates

图8 开孔压缩层压板损伤起始失效模式Fig.8 Failure modes of OHC laminates damage initiation

从图9可以看出，开孔板最终失效时，45°和90°层主导失效模式为基体膨胀和扭曲变形失效，0°层为纤维压缩失效，同时有基体膨胀和扭曲变形失效.

图9 开孔压缩层压板断裂失效模式Fig.9 Failure modes of OHC laminates fracture

将不同失效时间SIFT/ATM预测的压缩强度连接，构成开孔压缩强度控制曲线，如图10所示.从图中可以看出，本文预测结果与试验结果吻合很好.

图10 TR30S/epoxy开孔层压板长期压缩强度预测结果与试验结果Fig.10 Predicted and experimental OHC long-term strength of TR30S/epoxy

5 结论

1)本文对纤维的失效机理进行分析，对应变不变量失效理论的纤维失效准则进行了改进，并结合加速试验方法，构建了 SIFT临界值控制曲线.

2)根据SIFT临界值控制曲线可以看出，纤维的拉伸破坏应变基本不受时间影响;纤维压缩和基体膨胀失效应变随着时间增加而减小;基体的扭曲变形失效应变由于泊松比的变化随着时间增加而增大.

3)建立了基于SIFT/ATM和渐进损伤分析相结合的方法，预测了准各向同性开孔层压板的压缩失效过程和压缩强度，预测结果与试验结果吻合较好，验证了SIFT/ATM方法的合理性.

References)

［1］ Miyano Y，Kanemistu M，Kunio T，et al.Role of matrix resin on fracture strengths of unidirectional CFRP［J］.Journal of Composite Materials，1986，18(3):520-538

［2］ Miyano Y，Nakada M，McMurray M K，et al.Prediction of flexural fatigue strength of CFRP composites under arbitrary frequency，stress ratio and temperature［J］.Journal of Composite Materials，1997，31(6):619-638

［3］ Miyano Y，Nakada M，Cai H.Formulation of long-term creep and fatigue strengths of polymer composites based on accelerated testing methodology［J］.Journal of Composite Materials，2008，42(18):1897-1919

［4］ Miyano Y，Nakada M，Sekine N.Life prediction of CFRP/metal bolted joint under water absorption condition［J］.Journal of Composite Materials，2010，44(20):2393-2411

［5］ Miyano Y，Nakada M，Nishigaki K.Prediction long-term fatigue life of quasi-isotropic CFRP laminates for aircraft use［J］.International Journal of Fatigue，2006，28(10):1217-1225

［6］ Nakada M，Miyano Y.Accelerated testing for long-term fatigue strength of various FRP laminates for marine use［J］.Composite Science and Technology，2009，69(6):805-813

［7］ Nadaka M，Miyano Y，Cai H，et al.Prediction of long-term viscoelastic behavior of amorphous resin based on the time-temperature superposition principle［J］.Mechanics of Time Dependent Materials，2011，15(3):309-316

［8］ Cai H，Mizotani T，Nakada M，et al.Time-temperature dependent flexural fatigue behavior of honeycomb sandwich composites［C］//Proceeding of The 14th International Conference on Composite Materials(ICCM-14).San Diego:Society of Manufacturing Engineers，2003:1395-1400

［9］ Iwai K，Cai H，Nakada M，et al.Prediction of long-term fatigue strength of quasi-isotropic CFRP laminates with a hole under compressive loading［J］.Science and Engineering of Composites Materials，2011，17(4):227-242

［10］ Goose J H，Christensen S.Strain invariant failure criteria for polymers in composite materials［C］//19th AIAA Applited Aerodynamics Conference.Seattle:American Institute of Aeronautics ＆ Astronuatics，2001:1-11

［11］ Tay T E，Liu G，Tan V B C.Damage progression in open-hole tension laminates by the SIFT-EFM approach［J］.Journal of Composite Materials，2006，40(11):971-992

［12］ Sun X S，Tan V B C，Tay T E.Micromechanics-based progressive failure analysis of fibre-reinforced composites with non-iterative element-failure method［J］.Computers and Structures，2011，89(11):1103-1116

［13］ Sihn S，Tsai S W.Prediction of fatigue S-N curves of composite laminates by super Mic-Mac［J］.Composites Part A:Applied Science and Manufacturing，2005，36(10):1381-1388

［14］ Cai H，Murase T，Nakada M，et al.Time-temperature dependent strength of CFRP laminate based on strain invariant failure theory［C］//The Sixth China-Japan-US Joint Conference on Composites Proceedings.Beijing:China Academic Journal Electronic Publishing House，2004:12-17

［15］ Cai H，Miyano Y，Nakada M.Long-term open-hole compression strength of CFRP laminates based on strain invariant failure theory［J］.Journal of Thermoplastic Composite Materials，2009，22(1):63-81