几类中立型Lurie系统的稳定性及鲁棒绝对稳定性概述
2014-12-02王玉红包俊东
王玉红,包俊东
1.内蒙古化工职业学院,内蒙古呼和浩特 010070
2.内蒙古师范大学数学科学学院,内蒙古呼和浩特 010022
0 引言
利用数学上的理想模型为许多实际系统建模已成为当今解决问题的方法之一。而中立型Lurie 控制系统就是一类非常重要的数学模型。本文探索了几类时滞中立型Lurie 系统的稳定性和鲁棒绝对稳定性问题,寻找使得系统稳定的条件,这些系统来源于现实生活中广泛存在的问题,很有研究价值。
1 发展概况
首先,在实际的控制系统中,系统状态的变化速度可能会含有时滞,即系统变化速度不仅依赖于当前信息,而且还会依赖于过去的信息。2005 年,徐炳吉、沈轶、廖晓昕巧妙构造Lyapunov 泛函,研究了一般中立型Lurie 控制系统
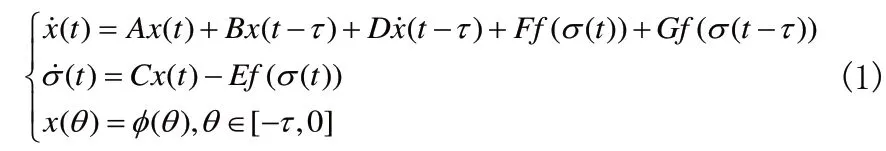
得到系统(1)绝对稳定性的时滞相关、时滞无关的若干充分条件;2006 年,董晓梅、赵峥嵘引用李亚普诺夫方法和线性矩阵不等式,对一类中立型Lurie 系统
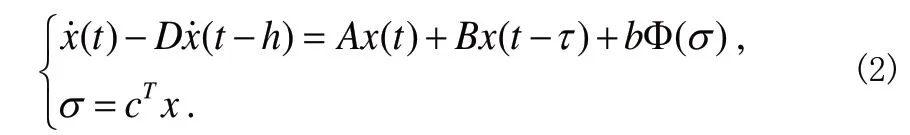
进行讨论,得到系统绝对稳定的又一新的时滞相关准则;2005年,徐炳吉、刘新芝又利用Lyapunov 泛函方法,对中立型Lurie 控制系统

进行了绝对稳定性分析,得到了系统时滞相关条件和时滞无关条件,结果均是用线性矩阵不等式形式表示的。
其次,实际系统的滞后和结构扰动也是系统不稳定的重要因素,尤其是不确定时滞系统的鲁棒控制问题倍受关注。目前,在系统的鲁棒稳定性分析、鲁棒控制器设计、鲁棒性能分析等方面都获得了大量的研究成果[1 -3]。Lurie 控制系统是一类非常重要的控制系统,其相关鲁棒稳定性研究已有大量的研究成果。
2003 年,彭达洲、胥布工针对一类具有范数不确定参数和未知常数时滞的Lurie 型不确定系统
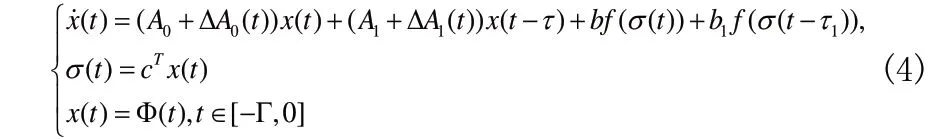
其中 0 ≤τ,τ1≤Γ 为未知常时滞,建立了系统的时滞相关鲁棒绝对稳定性判据,并且所得结果用LMI 形式表示,应用Matlab LMI 工具箱迭代求解可以得到时滞的上界,从而可对系统的允许时滞做出较高的估计。
2004 年,李宏飞、罗学波考虑了系统矩阵具有可加式扰动的不确定中立型Lurie 直接控制系统
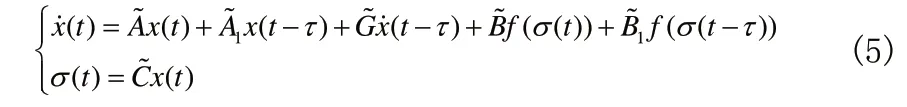
并给出了基于求解线性矩阵不等式的鲁棒绝对稳定性条件,且这些条件是时滞相关的;同年,他们又对如下一类Lurie 间接控制系统
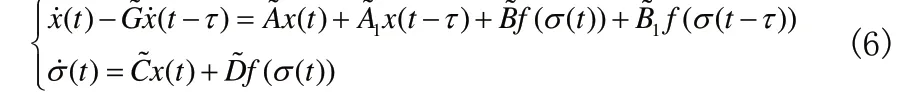
进行了鲁棒稳定性分析,借助于Lyapunov 泛函构造方法,给出了关于Lyapunov 泛函中正定矩阵和积分项参数的线性矩阵不等式的稳定性判别准则,且这些准则是与时滞量的大小无的。

2005 年,徐炳吉、廖晓昕考虑了不确定性中立型Lurie控制系统并应用Lyapunov 泛函方法,对系统(7)的鲁棒绝对稳定性进行了研究,并给出鲁棒绝对稳定的时滞相关充分条件。
2006 年,王海龙又讨论了单时滞不确定Lurie 控制系统
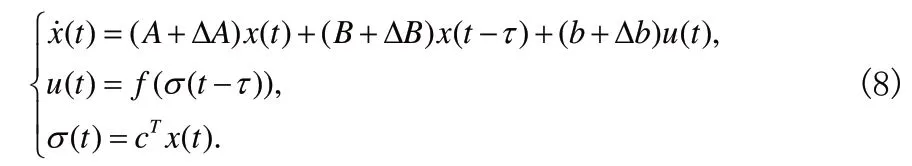
以及多时滞多执行机构的Lurie 系统
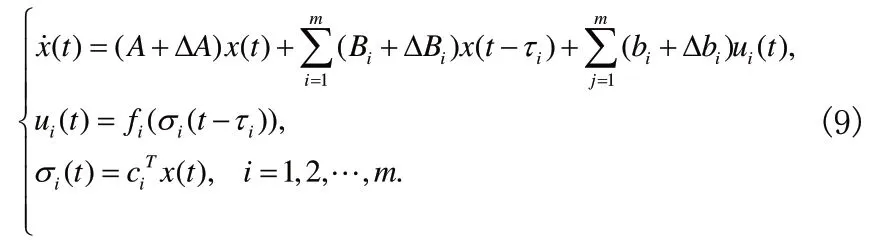
并巧妙构造Lyapunov 泛函,合理引用Razumikhin 定理,推导出系统在非结构不确定性下鲁棒绝对稳定的充分条件。
2 相关研究成果的推广
1)控制项具有时滞的中立型Lurie 控制系统的绝对稳定性
考虑系统

利用M-矩阵的性质[4],并构造出合适的Lyapunov 泛函得到该系统相关结论,相关证明过程相见文[2]。
2)一类一般非线性中立型Lurie 控制系统的稳定性
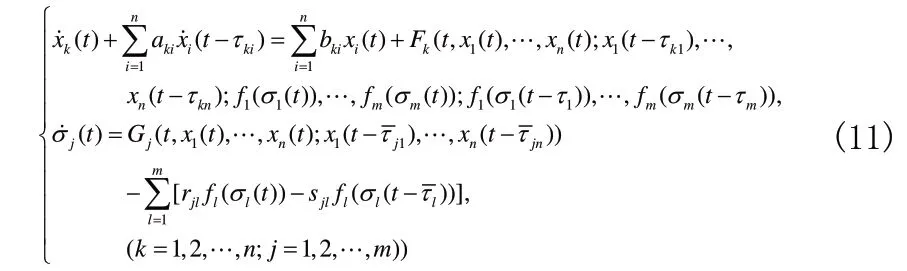
考虑系统利用M-矩阵的性质,并构造出合适的Lyapunov 泛函得到该系统零解是一致渐近稳定的,相关证明过程相见文[2]。
3)一类不确定性中立型Lurie 控制系统的时滞相关鲁棒绝对稳定性
考虑系统
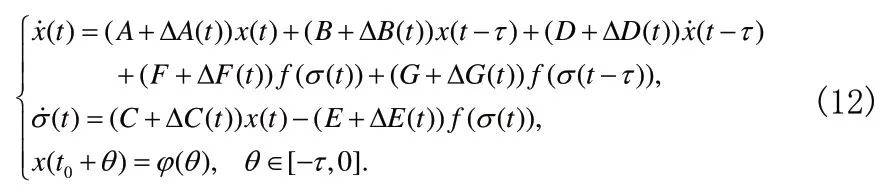
利用Schur 补引理、S-过程方法和相关引理,并基于线性矩阵不等式处理方法给出了系统(12)鲁棒绝对稳定性的判别条件,相关证明过程相见文[3]。
3 研究目的和意义
近年来,Lurie 型控制系统的稳定性问题,倍受专家学者们的关注,这是因为很多控制系统都可以转化为Lurie 型非线性控制系统,因此,对此类控制系统的稳定性理论分析、实际设计等有着实际价值。专家学者们巧妙地引用各种有效的方法,完成了控制系统的分析研究、综合设计,并得到相应控制系统绝对稳定性及鲁棒绝对稳定性的充分条件和在特殊情况下的充要条件。
然而,要么是实际现象过于复杂,要么是理论成果很理想化,这是目前存在的现状。正如我们所研究的实际控制系统一样,有待于解决的问题很多,比如:其一,时滞的存在:现实中的闭环控制系统都存在滞后,滞后现象常常会使系统的性能变差甚至可能会导致系统振动以及不稳定,正因如此,专家学者们开始研究具有时滞的系统。目前,关于Lurie 型时滞系统的研究已经取得了丰硕的成果。然而,无论是系统的状态、状态的变化速度亦或是对系统实际加以控制的控制器都不仅仅依赖于当前的信息,而且还依赖于过去的信息,于是由于在这里引入系统的过去状态信息,若是此信息对滞后系统的影响较小,则系统尚可有效,若是影响较大,则原控制条件的控制效果可能不好,因此探讨滞后型和中立型Lurie 系统的绝对稳定性是有实际意义的;其二,系统模型的不确定性和参数摄动:为了对系统进行综合,要建立起系统的模型,而且系统的综合结果都是相对于所建立的模型而得到的。实际控制系统中的不确定因素、建模过程中的误差,这些都是不可避免地存在着的,而且可能是各种各样。因此,相对于一个实际系统来讲,所导出的模型一般都是比较理想化的模型,但是人们仍然期待,期待实际的控制系统能够具有一定的抗干扰能力。
进入21 世纪后,已有的研究成果已经远不能满足时代的需求了。因此,进一步探索不确定性的Lurie 系统,尤其是探索不确定时滞型Lurie 控制系统的鲁棒稳定性已经是时代需求的事情了。
[1]马新军,胥布工.不确定时滞系统鲁棒稳定性及鲁棒控制研究.华南理工大学博士论文,2005.
[2]王玉红.具有时滞的Lurie型控制系统绝对稳定性和鲁棒稳定性的研究.内蒙古师范大学硕士学位论文,2007.
[3]王玉红,包俊东.不确定性中立型Lurie控制系统的时滞相关鲁棒绝对稳定性[J].内蒙古师范大学学报,2014,43(5):1-6.
[4]George Poole,Thomas Boollon.A surrey on M-matrix,Siam Review,1974,16(4):419-426.
