考虑路径优化和变电站选址的空间电网规划分析

钟 红

国网江西省电力公司鹰潭供电分公司，江西鹰潭 335000

0 引言

随着经济的快速发展，社会对于电力的需求不断增加，电网工程的建设和完善也因此受到了社会各界的广泛关注。作为电力系统的重要组成部分，电网承担着连接发电侧和用户侧，输送电能的重要职能，其规划设计一直是电力系统研究领域的重点。但是在电力体制改革的影响下，电网的规划工作面临着许多新的问题和挑战，需要电力企业和相关管理部门的充分充分重视。

1 电网规划设计现状

在经济发展的带动下，我国社会对于电力的需求不断增加，原有的电力网络已经逐渐无法满足实际供电需求，跳闸、断电、短路等事故频繁发生，严重影响了供电的可靠性和安全性。因此，对电网进行重新规划设计，确保其能够满足社会对于电力的需求，是十分必要的。而随着电力体制改革的深化和人们环保意识的增强，电网的规划工作也开始面临着新的问题和挑战，这些问题主要表现在：1）在市场经济环境中，决策的分散化在很大程度上增加了电网规划协调的难度；2）可再生能源（太阳能、风能、水能等）的大规模接入，使得电网规划工作中存在许多的不确定因素；3）环境因素的多样性和复杂性使得电网规划建模和求解更加困难。对此，国内许多专业技术人员对展开了对于电网规划工作的探索和研究，并取得了相当显著的成果。但是相对来说，这些研究成果多是单独考虑输配电线路路径优化以及电网网架规划，而忽略了两者之间存在的密切关系。由此，本文对这些文献进行了总结，提出建立考虑路径优化的双层非线性空间电网规划模型，由遗传算法和动态规划法结合而成的混合优化方法进行求解，可以有效提高了空间电网规划的求解质量和求解效率。

2 考虑路径优化和变电站选址的空间电网规划

在GIS 技术发展的带动下，相关技术人员在电网线路的路径进行优化选择时，往往会借助GIS 技术，将矢量地图转化为相对规则的栅格地图，然后建立栅格的走向变量，采用动态规划法寻找变电站之间的最优线路径，不仅考虑了环境约束和投资成本，而且计算了地形斜坡对成本的影响。

2.1 栅格化三维地图

地图的栅格化在空间电网的规划中发挥着极其关键的作用，根据地图附带的环境信息，可以将其划分为相应的栅格地图，这里假设在同一个栅格中，同一类型的线路和变电站建设成本相同。结合相应的文献资料，可以得出栅格的线路综合成本矩阵和栅格的高度矩阵，如下式（1）和式（2）。

其中，bij表示栅格Cij上新建线路的单位化综合成本，而hij则表示栅格Cij的单位化高速。当变电站建设在不同的栅格上时，其投资成本也会存在一定的区别，假设综合成本矩阵为E，则与式（1）类似，矩阵中eij表示栅格Cij上新建线路的综合成本。

当栅格数量巨大时，可以采用模式识别法或者神经网络法，对栅格上线路的综合成本进行计算，如果必要，也可以对计算结果进行人工修正。

2.2 空间电网规划模型

1）上层问题

空间电网规划的上层问题，属于一个传统的电网规划问题，其目的主要是为了确定投建的候选路线，以及变电站的建设位置，在满足电网满负荷安全运行的前提下，确保电网投资和运行成本的综合最小。换言之，上层问题的优化目标，就是最小化投资成本和运行成本，由相应的公式表达，则

其中，表示年平均电价，Tmax表示最大负荷损耗小时数，t 代表年度索引，NT指投资回收年限，φ为年收益率，Ploss为有功网损，Nw为新建的变电站数量，w 指新建变电站索引，iw,jw表示变电站的建设位置。

2）下层问题

下层问题主要是线路路径的优化问题，其优化目标是最小化每一条线路的投资成本，用公式表示为

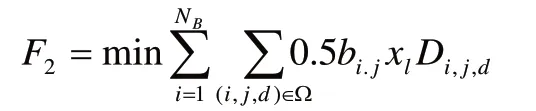
Ω={（i，j，d）|如果线路l 在Ci，j上选择方向d}

式中，Ω 表示线路l 选中栅格及其上方向的集合，Di,j,d表示线路在栅格Ci，j方向d 上的长度。

2.3 模型求解

电网的规划属于一个多决策变量、多约束条件的混合整数非线性规划问题，因此可以采用遗传算法进行求解。将每一跳候选线路的投建状态和变电站建设位置作为个体基因，其构成如图：

针对栅格地图上线路路径优化问题，可以采用动态规划法进行求解。其基本的思路为：对于一个栅格，如果始端栅格到其邻近8 个栅格的最优路径已知，则始端栅格到该栅格的最优路径只与邻近8 个栅格的最优路径有关。在实际计算中，如果邻近栅格的当前最优路径发生改变，则需要对栅格当前的最优路径进行及时更新，以确保路径选择的合理性。

为了充分发挥遗传算法和动态规划法的优势，本文提出了一种以遗传算法为主体的混合优化算法，遗传算法实现网架结构的优化和变电站选址，动态规划法优化线路路径。同时，为了提高求解效率，在算法中增加了一个记忆体，对最近经常用到的路径记录集合进行保存。一个路径记录由记录号、始端点、末端点、线路成本、线路长度和退出计数6 部分构成。当进行求解时，如果某线路的两端点存在与记忆体中，则可以直接从记忆体中得到线路的长度和成本，如果不存在，则利用动态规划法，对优化路径进行构建，从而极大地节约了计算时间。

这里以某省级电网的规划为例，对其进行简单阐述。该电网主网目前存在有402 个节点，502 条支路，结合电网的实际情况，以相应的220×220 栅格地图，对电网进行扩展规划，在电网中新增4 个变电站以及340 条支路线路。

整个求解过程耗时3671s，由于电网规划属于离线分析，因此对于计算的实效性并没有太高的要求，虽然计算耗时较长，但是可以满足实际应用的要求。

3 结论

总而言之，在经济发展的带动下，社会对于电力的需求不断增长，电网的规划问题也引起了社会各界的广泛关注。本文提出了一种考虑路径优化和变电站选址的空间电网规划模型，并采用综合了遗传算法和动态规划法优势的混合优化算法进行求解，保证了电网规划的合理性和可靠性，推动了我国电网建设的顺利进行。

[1]王学良.基于输电线路设计相关问题研究[J].建筑遗产，2013(10):272.