商业银行贷款组合均值——CVaR 优化模型研究

■史永奋

贷款风险对于银行业经营管理有着举足轻重的影响，其带来的信用风险也一直是商业银行经营管理的重点。本文界定的信用风险(又称违约风险)定义为:由于借款人、金融工具的发行人或者交易对手，由于其信用评级变动或者履约能力发生变化而不愿或无力履行合同构成违约，给另一方带来损失的可能性。

信用风险是人们认识最早的一类风险，也是银行业经营管理中面临的固有风险，世界银行对全球银行业危机的研究结果表明，信用风险是银行破产的主要原因。银行业的信用风险一旦发生，会给金融机构乃至整个市场带来重大损失，更有可能引发金融危机。因此《巴塞尔协议》(1988 年)就确定了信用风险设置最低资本充足率的基本框架;《新巴塞尔协议》(2006年)推荐使用内部评级法作为度量信用风险的基本方法，内部评级法中的四个主要参数分别为违约率、违约下的损失率、违约暴露和期限。银行可以根据确定的主要参数计算预期信用损失和未预期信用损失，并利用未预期信用损失确定经济资本和监管资本。王晓博[1]认为内部评级法可以使得银行在风险管理中将风险敏感性和激励相容性结合，为采用组合风险管理模型提供良好的基础。如何利用内部评级法的基本观点控制商业银行的信用风险就成为银行风险管理的主要任务。

一、商业银行贷款组合优化模型研究的必要性

由于银行在经营管理中会受到市场上各种不确定因素的影响，使得银行的实际收益与预期收益目标相比会发生偏离，造成银行资产可能会受到损失，所以商业银行为了控制其资产损失，需要合理配置资源，控制信用风险。

贷款组合风险作为银行业经营管理过程中面临的主要风险，其风险控制问题是全球银行业共同面临的问题，巴塞尔银行监管委员会于1988 年7 月开始就强调了控制信用风险对银行业发展的重要性。随着时间的发展，巴塞尔协议的内容得到不断充实，所体现的监管思想也在进一步深化，但是对于信用风险的监管始终贯穿在协议中。1994 年我国商业银行开始全面实行巴塞尔协议要求，1995 年又颁布《中华人民共和国商业银行法》，通过立法来实现银行贷款业务以及与之有关的资产比例的规定，2003 年中央要求将继续降低不良贷款比例当作金融工作的主要任务之一，而且随着银行业的发展，2012年中国银行业监管管理委员会发布《商业银行资本管理办法(试行)》，自2013 年元旦起开始实施。

随着我国银行业的发展，银行的不良贷款成为我国金融体系中一个非常大的风险隐患。上市银行2013 年年报显示，中国银行业不良贷款大幅攀升，其中五大国有银行不良贷款总额已达3743.15 亿元，同比新增近470 亿元。银行的不良贷款在严重的情况下可能会动摇金融体系，诱发社会的金融危机，影响经济增长。

我国银行业一方面希望通过贷款实现高收益，但是高收益往往对应高风险，因此有些银行为了控制风险，宁愿闲置资金也不愿将资金贷给企业，从而导致企业融资难，影响经济发展;另一方面，由于国有银行不良贷款资产规模比较大，面对银行业实施的“自主经营、自担风险、自负盈亏、自我约束”，迫切需要银行进行科学的贷款组合风险管理，合理配置资产份额，以实现在一定盈利水平下银行贷款损失的风险最小化。

商业银行贷款组合风险管理是银行资产配置与风险管理的主要技术方法，纵观20 世纪90年代以来银行危机案例的发生，其实质都是在于银行资产配置失误，因而提高资产配置效益对于银行的存续和发展是至关重要的。商业银行贷款组合风险管理问题实际上是贷款组合风险与收益的均衡问题，在以往的研究中，既有基于组合收益最大化的资产组合研究，又有基于风险最小化的资产组合研究，还有综合考虑收益和风险的资产组合研究，这些研究成果都为银行贷款组合风险管理提供了有利的工具，但是这些研究较少考虑银行资产的特点和《新巴塞尔协议》对银行风险控制的基本思想，本文结合资产组合理论的研究和银行风险管理的特点，建立贷款组合的均值-CVaR 优化模型。

二、贷款组合均值-CVaR 模型的设定思路

考虑到商业银行资产的特点和《巴塞尔协议》中内部评级法的基本思想，需要注意以下几个方面。

第一，银行资产要进行分类管理。银行的资产从风险性的角度来分析，可以分为风险资产和无风险资产，例如银行的存款准备金以及备付金等资产由于收益是固定的，没有波动风险，因此这些资产都属于无风险资产。而对于银行的各类贷款，由于存在信息不对称，借款人利用信息优势过分追求高收益而忽略风险，从而导致银行贷款出现违约的可能，这类资产归属于风险资产，对于风险资产的处理可以根据银行内部的数据结合这些资产的违约率和违约下的损失率将资产按照不同的信用等级进行分类。

第二，模型的建立要考虑收益和风险的有效统一。商业银行经营中的一个核心问题是风险与收益的权衡，在进行贷款组合选择时，通常会利用组合的收益情况评价该贷款项目的绩效，但是一般情况下收益高的项目通常风险也比较大，因此如何平衡收益和风险就是一个急需解决的问题。本文利用贷款组合收益的均值作为衡量组合收益的指标，而对于组合的风险指标，许多学者采用由摩根、美国银行和瑞士银行等金融机构于1997 年合作推出的Credit Metrics 模型，它是利用VaR 作为衡量信用风险的指标，但现实表明VaR 不是一致性风险度量，无法满足凸性的要求，并且VaR 主要度量了在一定置信度下风险头寸可能遭遇到的最大损失，忽略了后面的尾部信息即极端损失发生的情形。而Mausser 和Rosen[2]的研究表明，CVaR的最小化可以降低难以测度的风险指标VaR，节省银行的监管资本。王亮[3]将CVaR 与VaR 的性质进行比较，发现CVaR 不仅能提高风险管理信息的准确性，而且能够帮助管理者合理配置资源，优化资源配置。因此本文利用CVaR 作为贷款组合风险的衡量指标。

第三，充分考虑贷款企业之间的相关性。由美国的次贷危机可以看出，不同类型的贷款人由于受到宏观经济环境等影响，可能会同时出现大批量违约的情况，因此在建立贷款组合的优化模型时，不仅要考虑贷款人的违约分布，还需要考虑不同贷款损失之间的相关结构。经验表明，Copula 函数不仅可以很好地描述不同损失之间不对称、非线性的相关性，而且还可以捕捉到极端损失事件的尾部相关。Li[4]的研究表明将Copula 函数引入到投资组合的信用风险管理中可以提高模型预测的准确性;吴恒煜[5]的研究结果发现，t-Copula 函数度量投资组合信用风险最合适。因此本文利用Copula 函数来度量不同贷款损失之间的相关结构。

三、贷款组合均值-CVaR 模型的选择

商业银行的资产主要有两大类:一类是国家限定的资产或资金，其相应的收益率是固定的，没有波动性，不存在风险，设其收益率为r1，…，rn。假定这类资产主要有6种，其中现金的利率r1为0;法定存款准备金的利率r2为2.52%;系统内准备金的利率r3为2.52%;银行备付金的利率r4为2.52%;系统内拆借(限额内)的利率r5为3.00% ;系统内拆借(限额外)的利率r6为3.30%。另外一类是企业贷款，由于企业的类型不同，对于商业银行而言不同企业的贷款收益率也不相同，假设有m 个企业，其对应的收益率分别记为R1，…，Rm，其中R1表示第i 类企业的收益率，企业的收益率是随机变量，并且R1，…，Rm是相关的。设商业银行投资在两类资产上的权重分别为w1，…，w6和x1，…，x6，则商业银行的收益函数为:

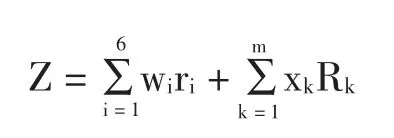
商业银行为了保证其收益，会对其相应的资产组合的收益进行限制，本文以商业银行收益函数的均值作为对收益的约束，假设收益函数的期望不低于给定的常数δ，贷款企业的最高贷款比例不超过80%。对于存贷款、备付金、拆除资金、法定存款准备金、系统内存款准备金、基于流动性的库存现金以及基于盈利性的库存现金的比重约束，可参看许文[6]的限制条件。

由于商业银行的信用风险主要来自于贷款风险，而对于贷款风险主要考虑的是资产组合的损失。因此假设商业银行一年期的贷款收益率为a，则商业银行的损失函数为:

利用上述分析可以建立贷款组合的均值-CVaR 模型为:

wi，xk满足限制条件

结合王秀国、邱菀华[7]的研究，利用蒙特卡洛模拟的方法可以对上述模型进行求解。

四、贷款组合均值-CVaR 优化模型的效果

由于许文[6]文中的数据是由银行的实际贷款数据进行加工处理得到的，比较真实，而且选取的贷款企业有一定的代表性，可以说明要解决的问题，因此下面利用其数据对均值-CVaR优化模型的效果进行分析。

在求解过程中，首先需要确定各企业的贷款损失率的边缘分布，一般认为beta 分布可以很好地拟合，故本文假定七类企业的违约损失率服从beta 分布，且这七类企业贷款损失率的参数α 分别为168.3、179.3、13.1、72.4、330.4、1291.4、176.3，β 分别为14595、14398、1009、3639、11512、33802、12568。

对于这7 类企业贷款损失率的相关结构，本文利用Copula 函数刻画。由于正态Copula 函数适合刻画对称相依、不具有厚尾特征的多维风险因子，t-Copula 函数适用于刻画对称相依、具有一定厚尾特征的多维风险因子，且当t-Copula 的自由度趋向于无穷时，它近似等于正态-Copula，本文分别利用正态Copula 函数和t-Copula 函数分别刻画损失率之间的相关结构。令δ=3.244%，β=95%利用蒙特卡洛模拟的方法求解均值-CVaR 优化模型。

如果采用正态Copula 函数，可以得到w1=0.0006，w2=0.06，w3=0.07，w4=0.1592，w6=0.0569，x1=0.2853，x2=0.3208，x3=0.053，x4=0.042，其余投资权重均为0，对应的VaR 为0.0141，CVaR 为0.0429。如果采用自由度为1的t-Copula 函数，则投资权重w4变为0.1826，w6变为0.055，x1变为0.5683，x2变为0.0362，x3变为0.07，增加x5为0.02，相应的VaR 为0.0140，CVaR 为0.0479。当t-Copula 函数的自由度变为5 时，w4变为0.1907，w6变为0.0543，x1变为0.504，x2变为0.088，x3变为0.066，x4为0.0244，相应的VaR 为0.0140，CVaR 为0.0462。

由所得结果可以看出选择不同的Copula 函数对VaR 值的影响不大，但是CVaR 值的变化比较大，这体现了企业的损失率具有“尖峰厚尾”的特征。对于t 分布而言:自由度越小，曲线越低平，尾部也就越大;自由度越大，曲线越接近于标准正态分布。所以自由度为1 的t-Copula 函数计算得到的CVaR 值最大，这是与t分布的特征相吻合的。从CVaR 值与VaR 值的比较来看，CVaR 比VaR 要大，普遍是VaR 的三倍左右，这说明贷款损失的尾部比较大，因此用均值-CVaR 模型构造的资产配置策略对风险的控制要优于一般的均值-VaR 模型得到的资产配置方案。

上述结果是在组合的平均年收益率不低于3.244%的情况下得到的，其实参数δ 值的改变也会影响到商业银行的各类资产投资比例，从而使得银行面临的风险发生变化，因此本文利用自由度为5 的t-Copula 以及β=95%置信度下在不同的收益率δ 下，计算银行的各类资产的投资比重和相应的CVaR 值，可以得到当δ分别为0.03144 和0.03344 时，w4分别为0.2884 和0.1033，w6分别为0.0465 和0.0613，x1分别为0.3110 和0.4356，x2分别为0.2235和0.2382，x3分别为0 和0.031，相应的CVaR分别为0.0414，0.0487。

由所得结果可以知道，随着收益率δ 的增加，CVaR 值逐渐增大，这是因为银行改变了其投资组合，增加了第3 类企业的贷款比例，减少了无风险资产的持有比例，使得银行所面临的贷款风险越大，相应的收益率δ 越小，银行对各类企业的贷款比例会相应减少，其投资行为会变得比较保守，这与银行在经济萧条时期所做出的决策相符合，当银行面临的外界环境萧条时，银行持有的无风险资产比例增加，并对各类企业的收益率要求提高，使得一部分企业得不到贷款。

本文的数据来自许文[6]，但本文的模型与其不同之处在于，许文的研究是针对银行的收益最大化的，只是利用了各贷款企业的相关系数及其期望与方差，并没有考虑贷款企业之间损失率的分布结构，将其结果与正态-Copula 函数计算出来的权重进行比较，可以发现本文的权重中增加了银行备付金w4的比重，减少了系统内拆借(限额外)w6的比重，对于7 类企业的贷款权重，一年期贷款同样的没有对第5、6、7 类企业进行贷款，与许文相比也相应地减少了第3、4 类企业的贷款比重，增加了第1、2 类企业的贷款比重，本文计算出CVaR 值为0.0429，是VaR 值0.0141的2.94 倍，说明其尾部风险是比较大的，因此CVaR 更能体现投资组合的潜在损失，将CVaR作为约束条件比其他方法更为保守和安全。

[1]王晓博.《新巴塞尔资本协议》与我国商业银行信用风险内部评级制度的国际接轨[J].商业研究，2006，(24).

[2]Mausser H，Rosen D.Applying Scenario Optimization to Portfolio Credit Risk.Algo Research Quarterly，1999，(2).

[3]王亮.基于CVaR 模型的风险度量[J].统计与决策，2011，(8).

[4]Li D X.On default correlation A Copula Function Approach.Journal of Fixed Income，2000，(9).

[5]吴恒煜.随机挽回率马儿可夫链模型下信用差价衍生品定价[J].系统工程，2006，(1).

[6]许文，董贺超，迟国泰.商业银行贷款组合动态优化模型研究[J].管理学报，2006，(6).

[7]王秀国，邱菀华.基于CVaR 和Monte-carlo 仿真的贷款组合决策模型[J].计算机工程与应用，2007，(4).