基于退化数据的微陀螺仪可靠性评估

于丽霞，秦 丽

（中北大学仪器科学与动态测试教育部重点实验室，山西 太原 030051）

0 引言

微机械陀螺仪以其体积小、重量轻、功耗低、全固态和动力学性能好等特点，广泛应用于灵巧弹、制导炮弹、战术武器等领域。随着微陀螺仪应用领域的不断扩大，其使用寿命、可靠性指标的获取日益重要。

传统可靠性评估技术以失效寿命为基础，所以在可靠性试验中仅记录样本的失效时间，而对于高可靠长寿命的产品，利用加速寿命试验或恒定应力试验难以获取准确的失效时间［1－5］。在这样的背景下，研究者开展了基于性能退化的可靠性试验与评估方法研究。北航的晁代宏［6］利用性能退化数据研究了卫星用光纤陀螺空间辐射环境下的可靠性评估方法；国防科技大学的邓爱民［7］对高可靠长寿命产品的可靠性技术做了全面系统的研究。因此，通过对表征样本功能的关键特征量连续测量，得到试验数据随时间的变化规律，并利用统计推断的方法就可以对样本的可靠性进行预测。

本文结合微陀螺仪的应用背景，在不改变失效机理的前提下，研究了温度应力下如何通过退化试验获得微陀螺仪零偏稳定性随时间的退化轨迹，进而建立退化模型，并通过合理的外推方法得到微陀螺仪在正常应力下的可靠度评估结果。

1 微机械陀螺仪的原理及特征参数选取

图1是微机械陀螺仪的模型，外加静电力施加到x方向驱动悬浮质量块做简谐运动，当微陀螺仪z轴方向有输入角速度时，根据哥氏效应原理，悬浮质量块将在y检测方向上产生运动。通过检测质量块与电极板之间位移变化转化的电容变化量获取z方向的输入角速度。

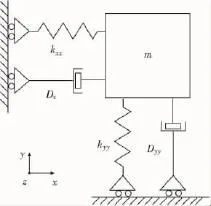
图1 微机械陀螺仪模型Fig.1 Model of the micro mechanical gyroscope

计算得到的稳态解表达式：

从检测模态的位移y（t）表达式知［8］：质量块在y检测方向上运动的振幅与输入角速度大小成正比，经过解调可得到输入角速度信号。

微机械陀螺仪的主要参数有标度因数、零偏、零偏稳定性、零偏重复性、随机游走系数等，其中，零偏和零偏稳定性是描述静态指标的主要特征量。针对微机械陀螺仪的工作特性，选择具有明确物理意义，且易于测量又稳定，并能客观反映样本工作状态的特性参数作为衡量退化性能的关键参数［9］。基于该原则，选取零偏稳定性作为退化试验的特征参数，因零偏稳定性能够反映MEMS陀螺仪的一次通电稳定性，是微机械陀螺的主要精度指标，且能够反映出微陀螺仪的性能退化。零偏稳定性的计算公式：

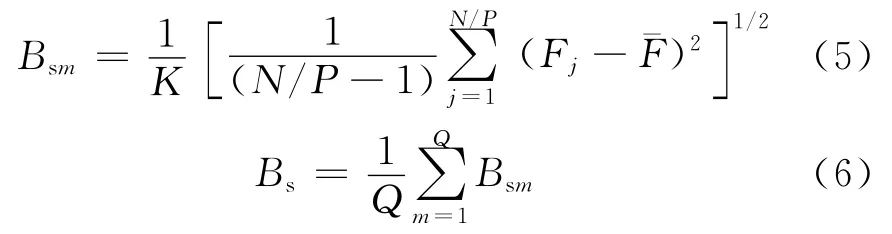
其中：K为标度因数；P为数据平均周期；Bsm为第m次测试得到的陀螺零偏稳定性；Q 为测试次数；Fj是每次采样的电压输出；F－为N次测试得到的输出平均值；Bs陀螺零偏稳定性。

2 基于退化试验的可靠性评估原理

基于退化试验的可靠性预测和评估理论包括三部分［10－11］：一是通过退化试验获取关键特征参数随时间变化的退化轨迹；二是根据退化量的变化规律建立参数退化模型和可靠度评估模型，并确定参数估计方法；三是根据参数确定的可靠性模型，预测样本的寿命和可靠度，基本流程如图2所示。

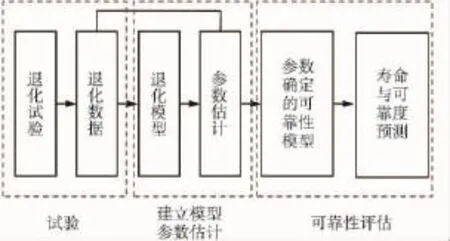
图2 基于退化试验的可靠性评估流程Fig.2 Reliability evaluation diagram based on degradation test

由于同类样本的总体退化趋势基本一致，而不同样本间具有随机波动性，因此可以用具有不同方程系数而形式相同的曲线方程来描述各个样本的退化轨迹。由此得到，不同样本达到失效阈值时的失效寿命在某种程度上也具有一定的随机性，因此可以利用分布假设检验的方法确定失效时间满足某种特定分布。

3 退化试验

针对某型号微机械陀螺仪进行退化试验，以获取陀螺仪零偏稳定性的退化数据［12］。试验样本为5个中精度的微机械陀螺仪，采用型号为CTP705的温度综合试验箱将陀螺仪的工作环境温度保持在45℃，每隔72h通过测试设备对陀螺仪的零偏、零偏稳定性和标度因数分别进行性能测试，总测试次数为25次，试验总时间1 800h，未出现失效。试验系统及样品如图3所示，实验数据结构表如表1所示。

图3 试验系统及样品Fig.3 Products and equipment of measuring

表1 微陀螺仪在45℃环境下退化数据结构表Tab.1Degradation data structure of MEMS gyroscope in 45℃

利用公式（5）和公式（6）对试验测得的数据计算并进行处理，得到微陀螺仪零偏稳定性随时间的变化曲线，如图4所示。

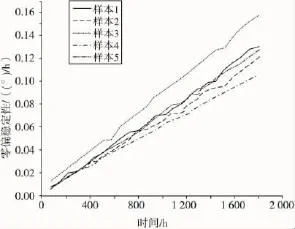
图4 微陀螺仪零偏稳定性的退化轨迹曲线Fig.4 Null bias stability degradation trend of MEMS gyroscope

4 寿命与可靠度评估

根据图4显示的微陀螺仪零偏稳定性随时间变化的实际退化轨迹，选择线性退化模型来讨论陀螺仪的可靠性问题，线性退化模型如下式：

其中，yi为零偏稳定性的退化量，i为试验样本数，t为试验时间，αi，βi是未知参数。

利用最小二乘法估计每个样本退化模型的参数，系数αi和βi的估计值如表2所示，拟合曲线如图5所示。

表2 各样本性能退化模型参数估计与失效寿命Tab.2 Performance degradation model’s parameters estimation and failure life of samples

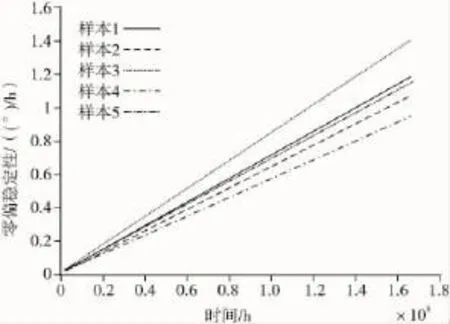
图5 退化轨迹拟合曲线Fig.5 Curve of fitting degradation trajectory

根据微陀螺仪的实际应用要求，将失效判据设定为零偏稳定性数值超过0.6（°）／h。由线性模型，依据图5所示的退化轨迹拟合曲线，当样本的零偏稳定性数值等于失效阈值Df＝0.6时，记录失效寿命时间，如表2所示。对样本的失效寿命进行偏峰度检验法，验证其分布规律，计算峰度值Ce得：

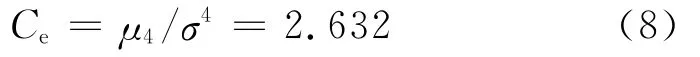
其中，μ4为四阶中心矩。

因峰度值接近于3，则可认为失效时间近似服从正态分布。计算失效时间满足正态分布时的均值与均方差：

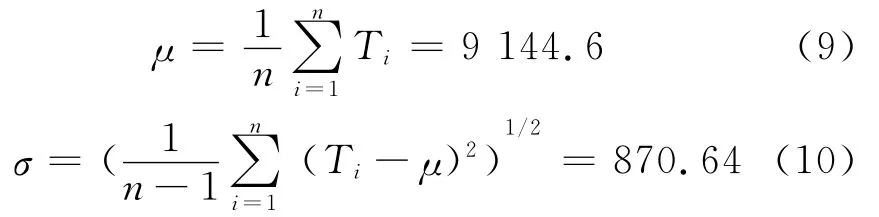
根据可靠性评估理论，在给定的时间t，产品的可靠度R（t）的点估计为：

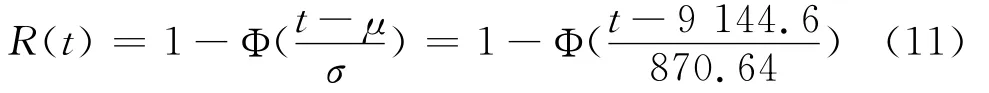
图6中给出失效寿命服从正态分布时的可靠度曲线。由图6可知，微陀螺仪在工作环境温度为45℃的条件下，工作6 133h时，陀螺仪的可靠度R（6 133）＝0.999 7，工作10 000 h可靠度R（10 000）＝0.151 85。

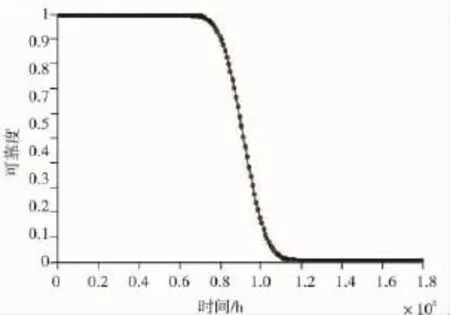
图6 微陀螺仪的可靠度曲线Fig.6 The reliability curve of MEMS gyroscope

5 结论

本文提出一种基于性能退化的微陀螺仪可靠性试验和评估方法。该方法首先根据微陀螺仪的工作特性，选择零偏稳定性作为衡量性能退化的特征参数，然后依据零偏稳定性的理论方程设计退化试验，再通过对试验数据分析获得零偏稳定性随时间的退化模型，设定失效判据进而建立参数退化规律与失效时间的关系以获取样本的寿命和可靠度指标R（t）。对某型号中精度微陀螺仪进行了温度应力下的性能退化试验，数据拟合表明，该陀螺仪零偏稳定性随时间的变化近似呈线性关系，利用统计推断方法估计各样本的退化模型参数。在失效判据设定为零偏稳定性超过0.6（°）／h时，得到了失效寿命服从正态分布时的可靠度曲线，可靠度为0.999 7时的陀螺仪寿命为6 133h。实践表明，基于性能退化的可靠性试验与评估方法过程简捷，计算量小，克服了传统可靠性分析方法依赖寿命数据的缺点，可作为同类产品难于获得失效数据情况下的可靠性评估与寿命预测的参考方法，并为下一步多应力下微陀螺仪的可靠性评估提供了依据。

［1］Luis A.Escobar and William Q.Meeker.A Review of Accelerated Test Models［J］.Statistical Science，2006，21（4）：552－577.

［2］Ying SHI，Luis A.ESCOBAR，William Q.MEEKER.Accelerated Destructive Degradation Test Planning ［J］.Technometrics，2009，51（1）：1－13.

［3］Haitao Liao，Elsayed A.Elsayed.Reliability Inference for Field Conditions from Accelerated Degradation Testing［J］.Inter Science，2006，53：576－586.

［4］Mikko Saukoski.System and Circuit Design for a Capacitive MEMS Gyroscope［D］.Helsinki：Helsinki University of Technology Faculty of Electronics，Commini－cations and Automation Department of Micro and Nanosciences，2008.

［5］刘凤丽.静电驱动微机械梳状陀螺仪中典型结构的可靠性研究［J］.探测与控制学报，2007，29（1）：72－75.

［6］晁代宏.基于性能退化的卫星用光纤陀螺可靠性评估［J］.红外与激光工程，2011，40（9）：1763－1767.

［7］邓爱民.高可靠长寿命产品可靠性技术研究［D］.北京：国防科技大学，2006.

［8］张云福.电容式微机械陀螺仪信号检测电路［J］.传感技术学报，2013，26（6）：878－882.

［9］马静.基于漂移布朗运动的光纤陀螺加速贮存寿命评估［J］.中国惯性技术学报，2010，18（6）：756－760.

［10］万夕干.基于加速退化试验的寿命与可靠性评估技术应用研究［J］.上海航天，2013，30（3）：60－68

［11］Jong in Park，Suk Joo Bae.Direct Prediction Methods on Lifetime Distribution of Organic Light Emitting Diodes From Accelerated Degradation Tests［J］.IEEE TRANSACTIONS ON RELIABILITY，2010，59（1）：74－90.

［12］周鹏斌.弹载惯性仪表的可靠性强化试验［J］.探测与控制学报，2010，32（4）：69－72.