基于CREO和ANSYS的减速器齿轮接触应力分析

武 智

（山西大同大学煤炭工程学院，山西 大同 037003）

减速器在现代机械中应用极为广泛，齿轮作为减速器中的主要部件，它的可靠性显得尤为重要，同时齿轮又是机械中广泛应用的传动零件之一，它具有功率范围大、传动效率高、传动比准确、使用寿命长等特点，但从零件失效的情况来看，齿轮也是最容易出故障的零件之一。据统计，在各种齿轮失效的故障中，齿面损伤是主要失效原因之一，所以在齿轮的设计中，其接触强度是重点研究内容。为此人们对齿面强度及其应力分布进行了大量的试验与仿真研究，但是齿轮工作条件的复杂性势必对试验测试带来困难，而仿真分析中建模的准确性、仿真软件对于非线性接触计算能力的分析等情况，在一定程度上影响了对齿面强度及其应力分布的研究进程。目前，随着大型仿真计算软件出现及运算能力的不断提高，能够得到精确的结果，为齿轮的设计分析和研究提供了较好的评价方法。

1 基于Creo减速器三维模型的建立

1.1 Creo软件简介

Creo是美国PTC公司（ParametricTechnologyCorporation）在整合Pro/E参数化技术、CoCreate直接建模技术和ProductView三维可视化技术后于2010年10月推出的新型CAD软件。它包括的模块主要有参数化设计及数控加工模块CreoParametric、直接建模技术模块CreoDirect、结构分析及热特性模块CreoSimulate、2D草绘模块CreoSketch、2D概念工程设计模块CreoLayout、管道和电缆系统设计模块CreoSchematics、3D技术插图模块CreoIllustrate、可视化CAD设计信息审阅模块CreoViewMCAD、可视化电子产品设计验证模块CreoViewECAD，其中Creo软件包含 Parametric、Direct和 Simulate，CreoView包含 CreoViewMCAD和ECAD，目前最新版本为Creo3.0。

1.2 减速器的虚拟装配

减速器零件主要由箱体、箱盖、齿轮、轴、端盖等常用件和螺栓、轴承、键等标准件组成。按照设计要求，将上述零件逐一进行建模，由于渐开线齿轮的齿形比较复杂，所以要对其进行参数化设计。第一步在工具选项卡中选择参数，并添加齿轮的各项参数；第二步在工具选项卡中选择关系，为圆柱齿轮添加几何尺寸，在FRONT平面上草绘四个圆，最后单击再生；第三步在模型选项卡中选择曲线、来自方程的曲线后在弹出的程序编辑器对话框中输入齿廓曲线方程，单击确定生成一条渐开线齿廓曲线；最后通过创建齿廓中心对称平面、经镜像、拉伸、阵列等命令最后生成的齿轮模型如图1所示。

图1 轮齿三维模型

图2 减速器装配模型

上述零件的三维模型全部生成后，就可以对减速器进行虚拟装配了。在Creo装配模块中使用贴合、平面和基准面对齐、坐标系各个轴相互对齐等约束命令将所有的零部件按使用要求装配在一起，装配好的减速器模型如图2所示。由于Creo采用的是单一数据库，即设计过程中的数据都来自一个库，整个装配体中的零部件保持相互关联性，当某个零件的尺寸需要修改时，则引用它的装配体也会自动更新，实时反应到减速器设计的各个环节上，这使得产品在设计过程中更方便高效，设计更优化。

2 齿轮精确有限元模型的建立

有限元模型不需要像CAD软件一样构造出产品外形和内部结构的每个微小细节，这样可以突出分析主要的影响因素、节省计算时间，例如有限元模型建立时，可以去掉远离关键部位的小孔，用光滑的圆孔代替螺纹孔，用尖角代替小圆角，用直线来代替小的过渡圆弧等。

若要评价有限元计算结果，首先要对计算结果进行解读，并不是每个计算结果值都可取，以齿轮接触应力有限元计算为例，在齿顶尖角与齿根部接触位置会出现应力最大值，这是有限元分析时将模型简化所致。现实中的齿轮都要对齿顶进行修缘，齿顶并不是尖角，但有限元模型将这些小的倒角忽略了，所以最大应力值就产生在单元棱边部位，而实际上这些地方并不是产生应力最大的位置。齿轮工作时节线附近经常发生点蚀，所以计算接触应力计算结果一般选取齿面接触位置的应力值。

网格数量对计算结果影响是必然的，但网格数量到一定值时，再增加已没有意义，所以合适的网格数量比较重要。以齿轮弯曲应力计算为例，分度圆与齿顶圆之间的网格数量对齿根弯曲应力基本没有影响，下面就对齿根过渡曲线不同网格数量的有限元结果进行对比。

以弯曲疲劳试验齿轮为依据，通过CAD建立几何模型，导入有限元软件，根据弯曲疲劳试验加载方式设置边界条件。轮齿采用扫略网格划分，沿齿宽方向固定19层单元，在图3所示的齿廓线固定8个单元，沿齿顶线方向固定8个单元，所以整个模型的网格数量由图4所示的齿根过渡曲线上网格数量决定，这个部位应力也是计算对象。

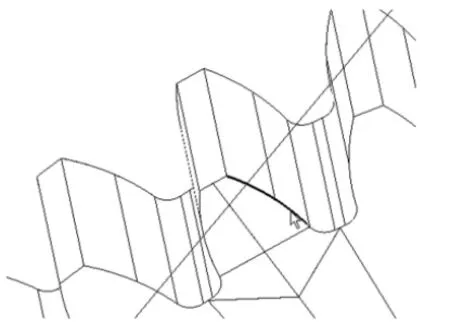
图3 轮齿齿廓线图

由于网格种子位置即是网格节点，齿根过渡曲线处网格数量由网格种子数量控制，分别在齿根过渡曲线处设置网格种子为 4、5、6、8、15、30个，分别对应的齿轮端面网格如图5所示。

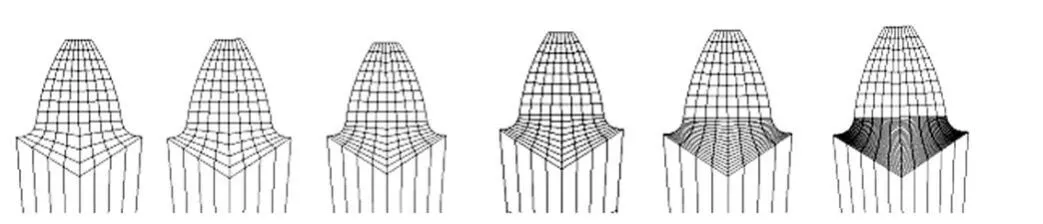
图5 不同网格数量的网格划分

下面就将不同网格的有限元在同一种载荷条件下，齿根应力极值进行对比，如表1所示。

通过表1可以看出随着网格数量增多，齿根应力增大，但齿根过渡曲线处种子数量由8增到30应力计算极值仅提高1%，所以计算时取8就可满足要求。

表1 载荷及对应计算应力

齿轮接触应力的有限元计算比弯曲应力计算复杂，接触处的网格应尽可能多，一般认为接触处单元边长十分之一赫兹半宽即可得到比较精确解。

3 试验齿轮接触应力有限元计算

试验中齿轮采用正反面交错搭接的啮合方式，接触齿宽为11mm，齿轮接触疲劳强度公式的是以节线处啮合位置以赫兹公式推导得出，且点蚀往往出现在节线附近，所以应分析节线的接触应力，其装配位置如图6所示。

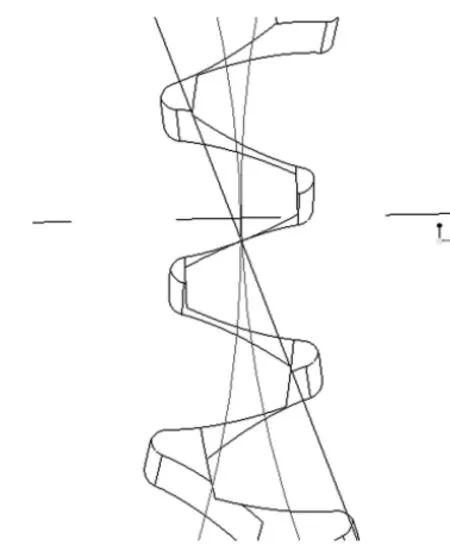
图6 装配位置示意图

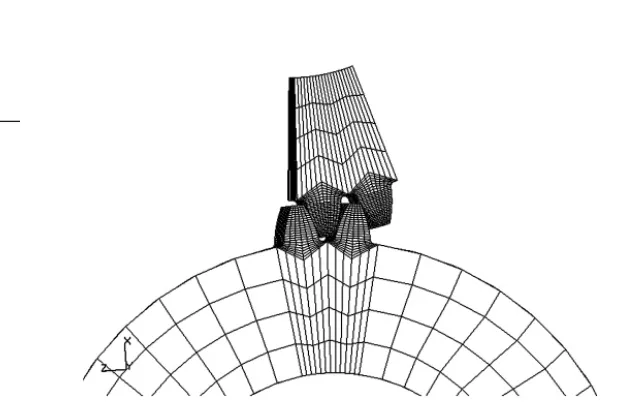
图7 接触应力分析有限元模型

如图7所示为导入有限元软件中划分网格建立有限元模型，依据接触疲劳试验第一级载荷，进行接触应力分析，扭矩为840 N·m，经有限元分析得到的应力云图如图8所示。

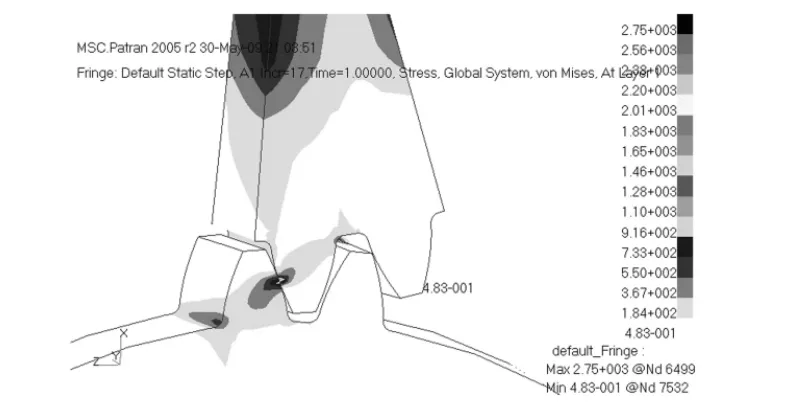
图8 有限元计算结果应力云图

从图9中看到应力最大值达到2 750MPa，公式计算仅1 769MPa，齿轮应力有限元计算结果一般比公式计算小，所以这个计算结果需要解读，单独将主动轮有限元模型提出，图9为主动轮应力云图，从中可以看出应力最大值在齿顶部位，这是因为有限元模型简化齿顶修缘所致，从试验中可知点蚀一般发生在齿轮节线偏下部位，接触应力较大部分应是节线附近，而不是齿顶。所以这个结果不可取。

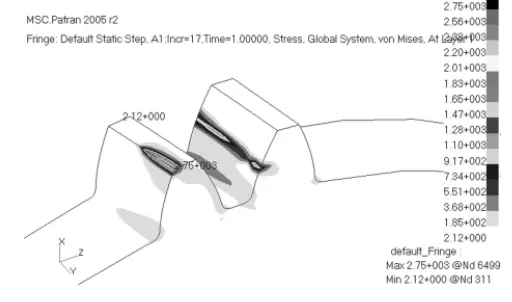
图9 主动轮应力云图

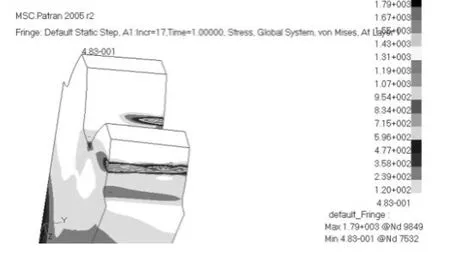
图10 从动轮应力云图

提取从动轮有限元模型，其应力如图10所示，可以看到动轮接触应力最大值为1 790MPa，且位置在节线附近，可以判断这个结果是可信的，后续所有分析结果都是以从动轮接触应力为准。

4 试验齿轮接触应力公式计算与有限元计算结果比较

利用有限元计算试验齿轮在如图6所示装配位置的接触应力，取从动轮接触应力的最大值作为计算结果。表2为不同载荷级别下，试验齿轮接触应力的公式计算结果与有限元计算结果的比较。

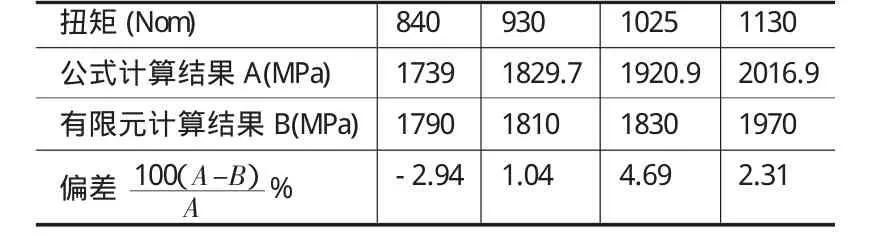
表2 试验齿轮接触应力计算结果对比

从表2可以看出有限元计算结果与公式计算值较为接近，仅存在5%以内的偏差，这是因为接触应力的非线性特性所致，影响公式计算和有限元计算的因素较多。

5 结束语

本文通过对减速器建模并仿真齿轮啮合过程，对在齿轮接触应力计算过程中，有限元模型简化及网格数量对计算结果的影响进行了对比分析，得出了最佳的评价方法；并将分析得到齿轮接触应力计算结果和用理论计算得到的结果进行对比，误差甚小，证明了有限元方法在解决该类问题上的可行性。通过有限元对齿轮进行仿真计算，可以大大减少了试验费用，缩短开发周期，并为齿轮的优化设计奠定了良好的基础。

[1]王 莺，叶 菁.基于SolidWorks的齿轮减速器三维设计及运动仿真[J].煤矿机械，2009，30（9）：234-236.

[2]李碧波，李素有，吴立言.渐开线齿轮接触应力分布规律的研究[J].机械与电子，2010，48（6）：4-7.

[3]黄泽平，马吉胜，吴大林.齿轮轮齿接触力仿真研究[J].机械传动，2007，31（2）：26-28.