炼厂自备码头港口吞吐量预测分析

中国石油大连分公司 李玉猛

一、自备码头港口吞吐量

港口吞吐量是港口最基本的生产指标，是组织港口生产、编制港口发展规划和进行港口建设的依据。同时港口吞吐量的大小可以反映港口所在城市及其腹地范围内的经济状态和发展水平，吞吐量的货物分类可以反映港口所在城市及其腹地范围内的产业结构和经济结构，吞吐量的进出口流向可以反映港口之间、城市之间、地区之间、外贸港口的国家之间等的经济和贸易关系。港口吞吐量发展是受到诸多客观因素影响和制约的,其预测成果的准确度、可靠性受人为主观因素的影响也是明显和直接的。

炼厂自备码头作为货主码头的一种形式，其港口吞吐量是所在城市港区吞吐量的重要组成部分。炼厂自备码头港口吞吐量的发展变化很大程度上取决于炼厂的原油加工能力以及炼厂实际原油加工量的发展变化，集中反映炼厂的运营状态，在一定程度上也反映了所在地区的经济运行状态。同时，随着炼厂本身不断增加从海上进口原油的加工量，港口吞吐量的发展又影响着炼厂的原油加工量。因此，一般的预测方法很难科学合理的对炼厂自备码头港口吞吐量的未来发展趋势进行预测分析，必须同时考虑到炼厂原油加工量和港口吞吐量的相互影响和制约才能做出准确预测。

为了能够准确把握炼厂自备码头港口吞吐量的发展趋势，并为进一步对码头通货能力与炼厂原油加工能力的匹配性进行评价提供基础数据，本文分别运用灰色理论GM(1,1)模型和MGM（1，n）模型对某北方炼厂自备码头的港口吞吐量进行预测，进行比较分析。

二、GM(1,1)模型和MGM（1，n）模型

(一)GM(1,1)模型简介

灰色系统理论是我国学者邓聚龙教授的首创，GM(1,1)模型是最常用的一种灰色系统模型，通过单变量的一阶微分方程模型揭示其内在发展规律，用于单一时间序列的建模和预测。

其解的离散描述形式为：

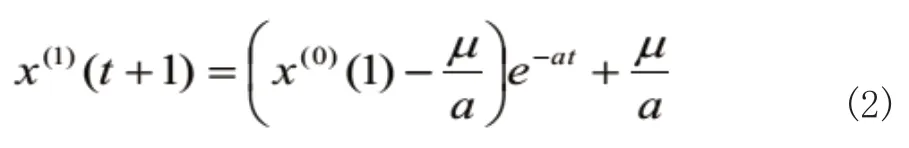
确定了参数a 和µ后，按照此模型类推即可得到预测的累加数列。通过验证后，再累减还原得到预测值。

预测步骤如下：

1.由原始数列x(0)按照下式计算累加生成数列x(1)：

2.采用最小二乘法，按下式确定模型参数

式中：

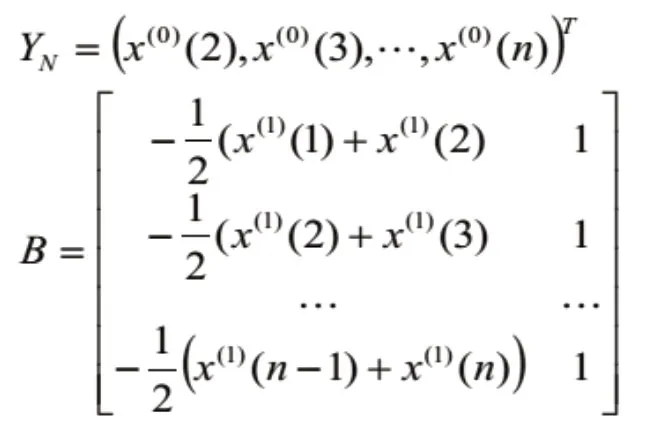
3.建立预测模型，利用(2)式求出累加数列。

4.采用残差分析法进行模型检验，或用计算后验差C和小误差概率P 的办法检验。

模型的精度分四级如表1 所示：

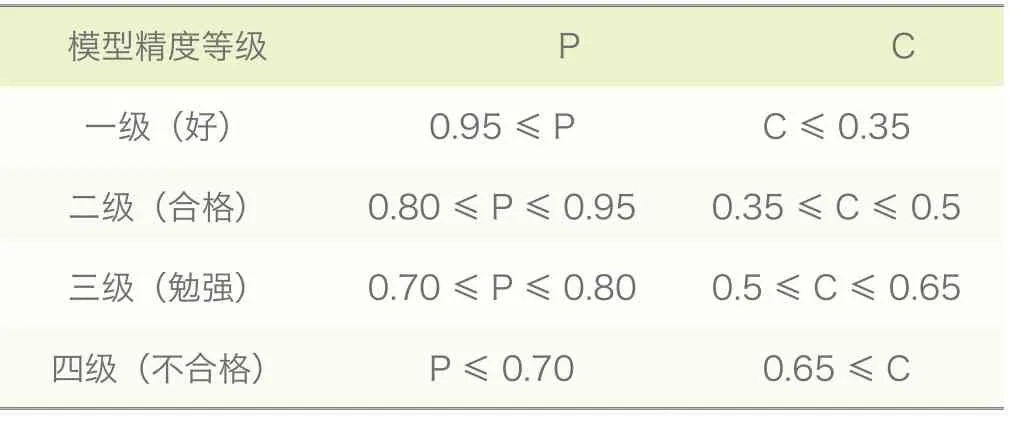
表1 灰色预测精度等级表

表中，

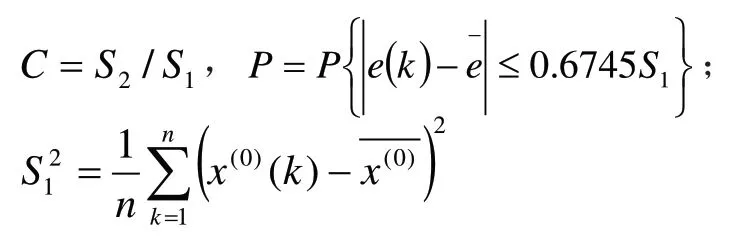
其中:

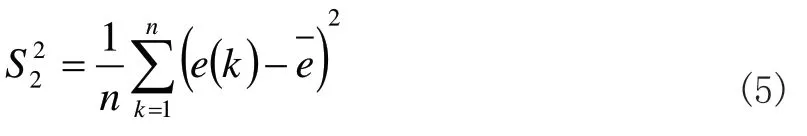
(二)MGM（1，n）模型

GM(1,1)模型是最常用的一种灰色系统模型，它通过单变量的一阶微分方程模型揭示其内在发展规律，用于单一时间序列的建模和预测。然而实际社会、经济系统中往往包括多个变量，各变量相互关联、共同发展。这时，每一个变量的发展变化都不是孤立的，一个变量要受到其他变量的影响，同时也影响着其他变量。为此，本文采用多变量灰色模型——MGM（1，n）模型，旨在从系统的角度对各变量进行统一描述。MGM（1，n）模型的形式是n元一阶常微分方程组，它是GM(1,1)模型在n元变量的情况下的自然推广，不是GM(1,1)模型的简单组合，也不同于GM(1,n)模型。具体原理如下：

其中，k=1, 2,…,m。

MGM（1，n）模型为n元一阶常微分方程组：

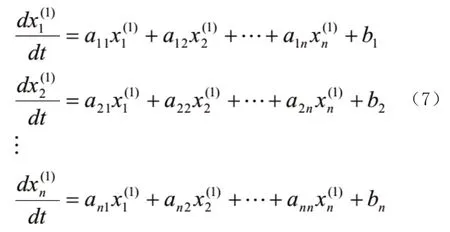
即：

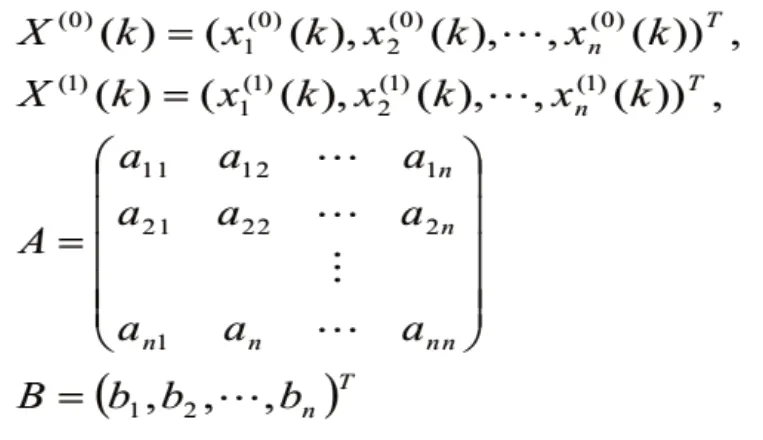
则（7）式可记为：

上式的连续时间响应为：

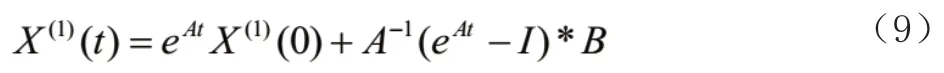
其中：

为了辨识参数A 和B，将（7）式离散化得到：

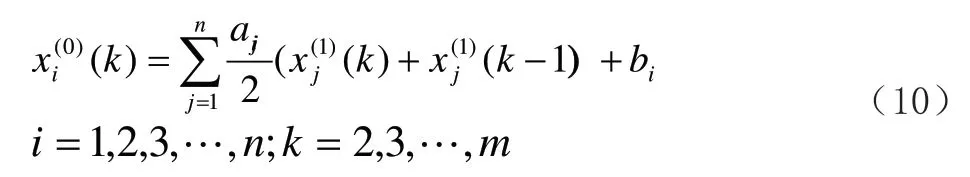
记ai=(ai1,ai2,…,ain,bi)T,i=1,2,…,n.。则由最小二乘法得到ai的辨识值。

其中：

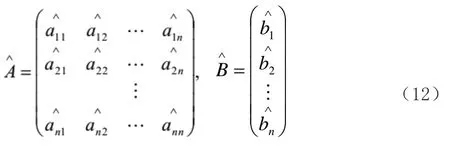
MGM（1，n）模型的计算值为：

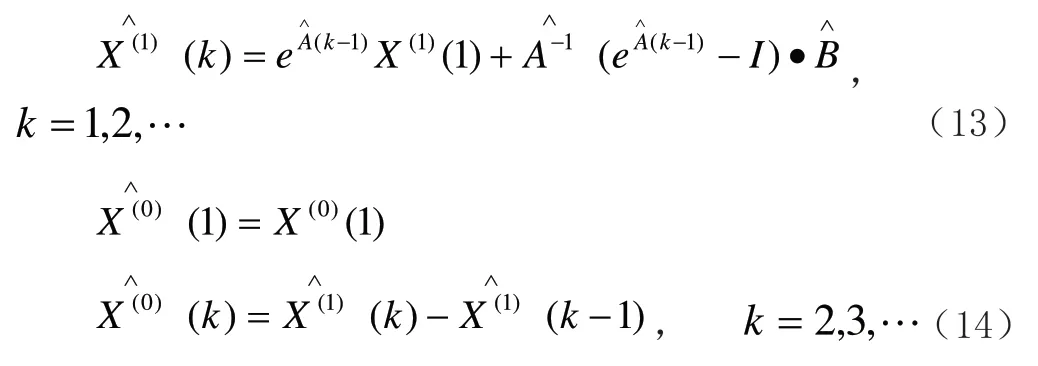
当n=1时，MGM（1，n）模型就退化为GM（1，1）模型；当B=0时，MGM（1，n）模型就是n个GM（1，n）模型的组合。由公式（9），（13）和（14）可知MGM（1，n）模型不仅可以建模还可以进行预测。

三、模型应用和比较

(一)炼厂自备码头的特点

某北方临海炼厂作为国内规模最大的炼油基地之一，不仅具备优越的地理位置和区位优势，而且具备完善的物流体系，如公路、铁路、管道和港口等，其中港口作为物流手段之一却承担着该炼厂绝大部分的物流任务，该炼厂拥有5000 吨级至10 万吨级的码头泊位15个，一直以来，20%以上的原油上岸和80%以上的产成品下海都是通过码头实现的。

某北方临海炼厂2007—2013年的原油加工量和码头吞吐量如表2所示。

通过以上统计数据，实际分析炼厂自备码头的的吞吐量和加工量的发展变化有如下特点：

1.炼厂自备码头港口吞吐量的实现是以炼厂原油加工量的实现为必要条件，也就是说炼厂炼油越多，码头吞吐量越大。然而，炼厂原油加工能力在某一个阶段内是一定的，是有上限的，原油加工量的发展变化不是永远呈递增趋势，最终原油实际加工量将稳定在炼厂最大炼油能力极限值附近浮动，此时炼厂自备码头港口吞吐量最终也将趋于某一定值。因此，炼厂自备码头的发展、建设和未来规划应当与炼厂炼能的扩能相匹配，共同发展。

2.炼厂自备码头港口吞吐量中原油进口量的增加在一定程度上不仅促进了炼厂炼量的增加，而且大大提高了港口自身的吞吐量，这一趋势将随着炼厂陆上原油供应量的逐年减少和海上原油供给量的逐渐增加而变得更加明显。比如，2009—2010年度炼厂原油加工量和吞吐量的逆行变化就是因为当年原油通过海上进口量几乎为零所造成的。

(二)模型计算和精度比较

利用MGM（1，n）模型得出的两序列的MGM（1，2）模型状态方程组为：

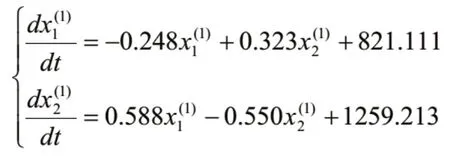
如对上述两个数列分别建立GM（1，1）模型，则可以分别得出原油加工量和港口吞吐量的灰色状态方程。

原油加工量的GM（1，1）模型为：

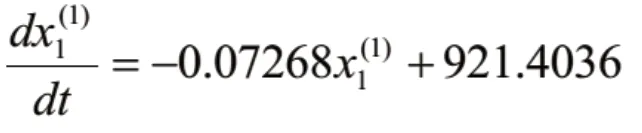
码头吞吐量的GM（1，1）模型为：

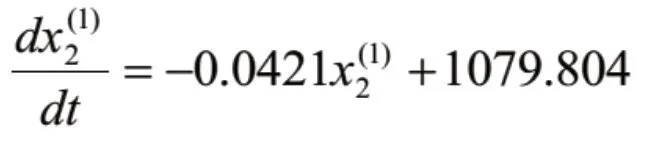
利用Malab 软件龙格库塔法求微分方程组，得出原油加工量和码头吞吐量两个数列的累加数列，然后还原成原始数列就是每个年度原油加工量和码头吞吐量的MGM（1，n）模型预测值。同样对于GM（1，1）模型，分别求解各自微分方程，得出原油加工量和码头吞吐量GM（1，1）模型预测值，比较如表3所示。

MGM（1，2）模型预测拟合图如图1所示：

GM（1，1）模型预测拟合图分别如图2，图3 所示：

表2 某炼厂2007—2013年的原油加工量和码头吞吐量 万吨

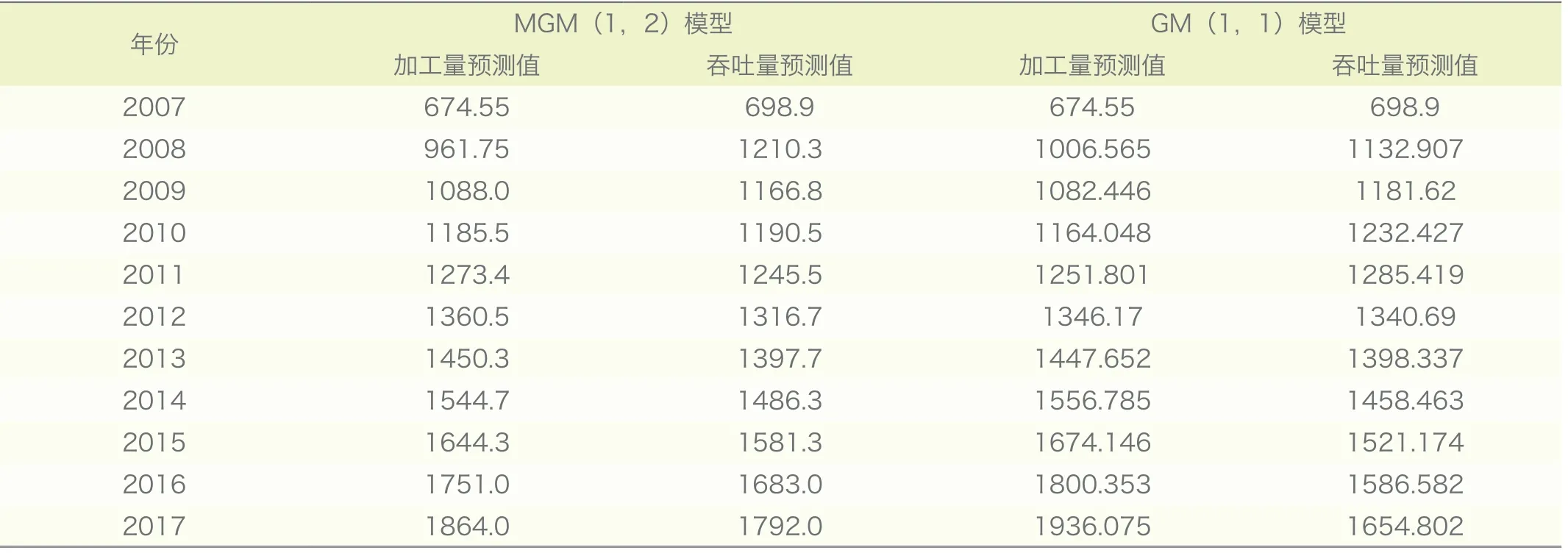
表3 GM（1，1）模型和MGM（1，2）模型预测值比较 万吨

通过用计算后验差C 的办法检验，分别求得C 值参考

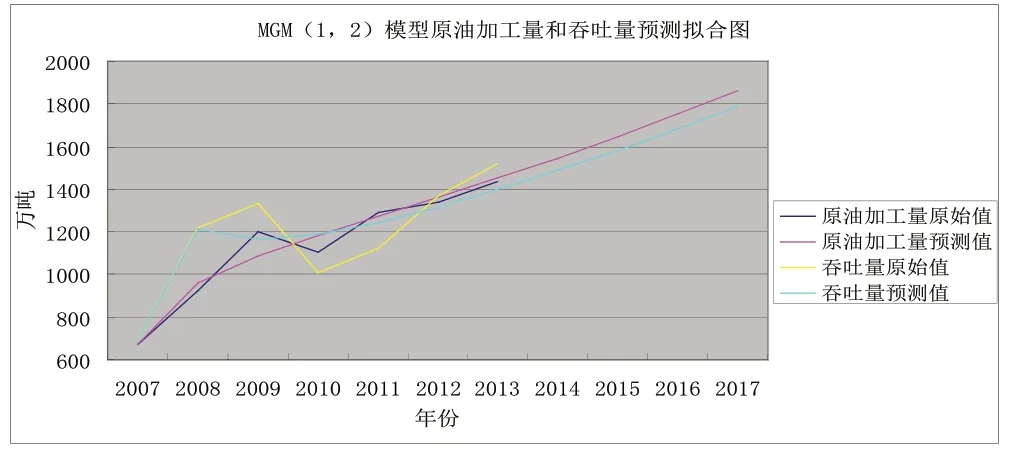
图1 MGM（1，2）模型原油加工量以及港口吞吐量预测拟合图

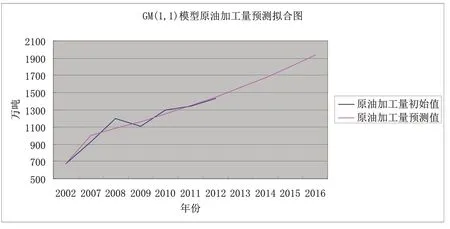
图2 GM（1，1）模型原油加工量预测拟合图

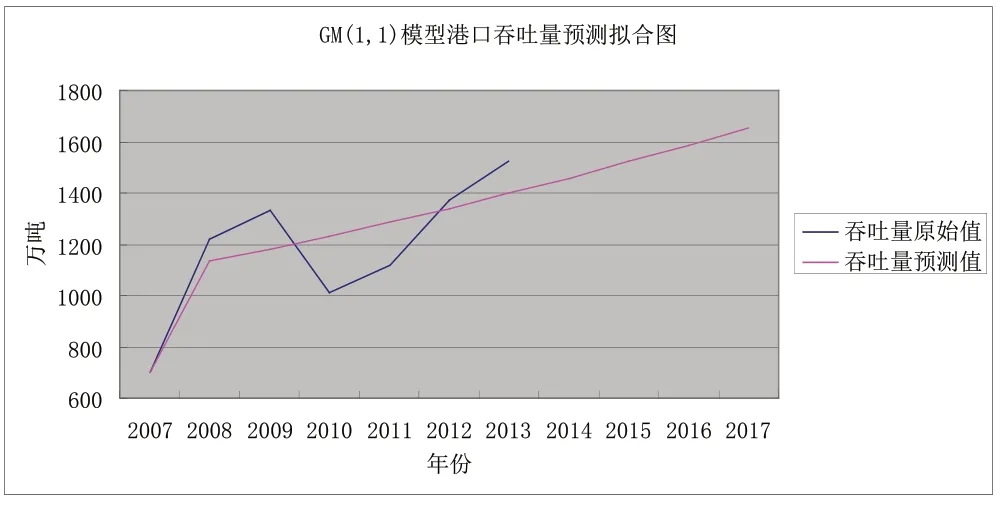
图3 GM（1，1）模型港口吞吐量预测拟合图

灰色预测精度表中的指标来判定原油加工量和码头吞吐量的预测精度，其中，MGM（1，2）模型原油加工量的C 值等于0.225，为一级精度；MGM（1，2）模型码头吞吐量的C 值等于0.459，为二级精度，均符合灰色模型关于预测精度的要求。

GM（1，1）模型原油加工量的验差C 值等于0.247，为一级精度，符合灰色模型关于预测精度的要求，而 GM（1，1）模型码头吞吐量的C 值等于0.527，为三级精度，属于勉强级别，如用于预测误差较大，很难提供参考价值。

另外，从两个模型的拟合图比较来看，MGM（1，2）模型更优。

四、结语

从系统的观点来看，MGM（1，n）模型是一种状态模型，它是单变量GM（1，1）模型在多变量的情况下的自然推广，旨在反映各变量之间相互制约、相互促进的关系。MGM（1，n）模型不能代替GM（1，1）模型，而是GM（1，1）模型的扩展和补充。同时，MGM（1，n）模型不同于GM（1，n）模型，是一种预测模型。

通过某北方临海炼厂的实例，对该炼厂的原油加工量和港口吞吐量两个变量建立MGM（1，2）模型，不仅预测炼厂在未来中长期原油加工量和港口吞吐量的发展变化趋势，而且揭示了炼厂自备码头港口吞吐量和原油加工量的内在联系。鉴于原油能源的稀缺性和不可再生性，世界上大多具有远见的发达国家都不再开采炼制本国的原油资源，我国也深刻认识到这一点，年进口原油过亿吨，并且进口依存度已经超过50%。因此，未来不仅沿海炼厂，甚至内陆炼厂都将可能全面炼制海外原油，那么具有自备码头的沿海炼厂只有在吞吐能力在达到炼油能力2 倍的条件下，方能满足炼厂产能的实现以及原油上岸和产成品下海的双重物流需求，届时甚至会出现炼厂向码头要炼量的局面。基于这一点，炼厂自备码头在规划建设过程中，未雨绸缪地预留一定的通货潜能以待挖掘是合理的。

[1]刘思峰,郭天榜,党耀国.灰色系统理论及其应用[M].北京：科学技术出版社,1999.

[2]邓聚龙.灰色预测与决策[M].武汉：华中工学院出版社,1986.

[3]欧轶.预测港口吞吐量方法的探讨[J].水运工程,2003（1）：22-25.

[4]冯英浚,翟军,盛建明．MGM(1,n)灰色模型及应用[J].系统工程理论及实践,1997（5）：109-113.

[5]顾光炎.对港口吞吐量统计制度改革的思考[J].港口装卸.1995（4）:34-35.