Excel中用Newton迭代法求解土的最优含水率和最大干密度的方法

彭永凯

（中铁隧道集团有限公司 工程试验中心， 洛阳 471009）

土的击实试验是铁路、水利（水库坝体）等工程设计和施工中必须使用的一项基础试验。目前，在击实试验的数据后处理上，用Excel已经非常普遍，不过仍有不少人在计算最优含水率和最大干密度的取值时采用图解或一元二次方程求最大值等方法。这些方法存在一定问题：图解法人为误差较大，一元二次方程求最大值法只有效利用了3个击实结果，误差较大。本文主要介绍在Excel中根据试验数据自动生成击实曲线，趋势线拟合公式，再用Newton迭代法求解高次方程，得出最优含水率和最大干密度的方法。

l 击实曲线与拟合公式的确定

按照《铁路工程土工试验规程》等有关试验规程的规定，同一土样须配制成5份以上不同含水率的试件，并分别测定含水率和相对应的试件重，从而得出不同含水量时土壤的干密度，再以含水率（%）为横坐标、干密度（g/cm3）为纵坐标，在坐标纸上绘出相对应的点，按数据点在图上的走势，绘成圆滑的曲线，曲线峰值对应的含水量与千容重即为最优含水率（ω）与最大干密度（ρd）。而此曲线即为击实曲线。

与击实试验规程的规定相对应的数值分析方法就是插值，常用的插值方法为Lagrange多项式插值。根据Lagrange插值多项式的定义可知其性质为：Lagrange插值多项式的存在是唯一的。也就是说通过已知的数据点只能做出唯一的一条曲线满足Lagrange插值函数的定义。Lagrange插值多项式对应的曲线通过所有的离散数据点，相关系数等于1。用鼠标右键单击图表上的任一数据点，单击弹出的快捷菜单中的“添加趋势线”，再单击“选项”按钮，选择“显示R平方值”可以验证插值多项式的相关系数等于1。对于击实试验数据来说，Lagrange插值多项式的阶数通常为试验数据的个数减去1，即当试验数据个数为5时，相应的Lagrange插值多项式的阶数为4，这时候干密度—含水量的关系表达式为：

其中，f(x)为当含水量为x时的干密度，x为含水量，a、b、c、d、e为插值系数。

2 击实曲线的绘制与拟合公式的生成

在Excel中：（1）采用表1（某土样击实结果）数据,以含水率ω(%)为横坐标、干密度ρd(g/cm3)为纵坐标插入仅带数据标记点的散点图。（2）在散点图中右键点击其中一数据标记点，选择添加趋势线，趋势预测/回归分析类型为多项式，顺序为4，勾选显示公式、显示R平方值。（3）右键点击所生成的公式，设置趋势线标签格式，选择数字，数字的小数位数修改为6。至此，所生成的图1散点图中趋势线为表1试验数据的击实曲线，图1中公式为拟合公式，R为相关系数。

表1 某土样击实结果

击实曲线为一凸曲线，极大值即为最大干密度，所对应含水率为最优含水率，可求解拟合公式（y＝f(x)）的极大值和对应的x取得。

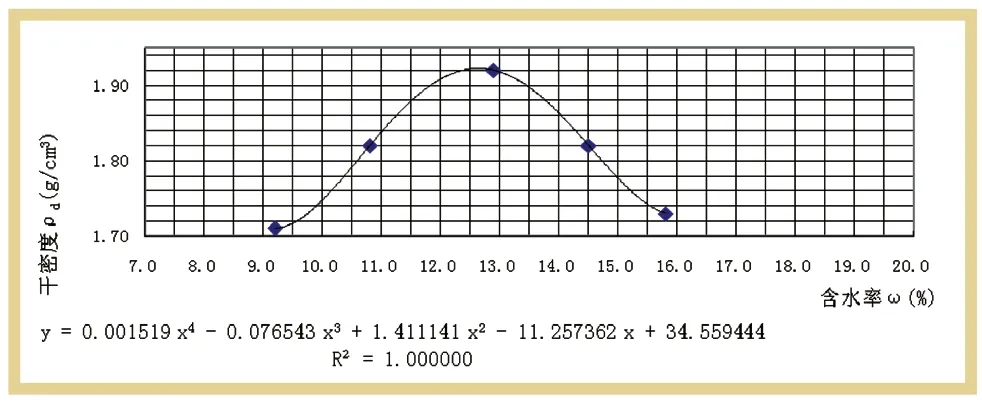
图1 由表1击实数据绘制的ρd-ω关系曲线与拟合结果

3 最优含水率与最大干密度的求解

在试验的含水率区间内，对拟合公式y＝f(x)求导，y为最大干密度值。为一元三次方程，可通过卡尔丹公式求解。卡尔丹公式判别条件较多，不利于Excel自动计算，本文用Newton迭代法求解，通用性强，并适用于更高次方程的求解。

Newton迭代法：设f(x*)=0, f'(x*)≠0,且f(x)在x*的领域N(x*)内有二阶连续导数，则Newton迭代格式：

至少是平方收敛的。

设：f(x) = ax4+bx3+cx2+dx+e= 0.001519x4-0.076543x3+1.411141x2-11.257362x+34.559444

则：f'(x)=4ax3+3bx2+2cx+d=0.006076x3-0.229629x2+2.822282x-11.257362

f"(x)=12ax2+6bx+2c=0.018228x2-0.459258x+2.822282

取x0＝12.9（表1某土样击实结果中最大干密度对应的含水率），用Newton迭代法迭代过程见表2。

表2 Newton迭代法迭代过程

由表2可知，该迭代计算收敛速度非常快，x2=x3=x4=x5=x6, x2即为最终迭代结果，是最优含水率。把最优含水率代进f(x) = ax4+bx3+cx2+dx+e，求得最大干密度f(x)＝1.92。

把计算结果（最优含水率12.6%，最大干密度1.92 g/cm3)与图1比较，可知此计算结果与从图上直接估读值接近，理论上精度更高。

在Excel中完成如上节中所述的步骤（2）和步骤（3）后，以后再有击实数据，则可以输入击实试验数据后自动生成击实曲线，求得最优含水率和最大干密度，省时、省力且精度良好。

4 结束语

土的最大干密度和最优含水率可以用数解法确定。本文重点介绍利用Excel处理击实数据，生成击实曲线并计算最优含水量和最大干密度的方法。文中举例介绍了本方法的核心内容，由于Excel最多可进行6阶多项式拟合，因此，本方法可以处理7个击实数据内的所有击实问题。

[1]黄 英，符必昌. 确定土的最大干密度和最优含水率 [J].岩土工程学报，2002，24（4）.

[2]王兵团，张作泉，赵平福. 数值分析简明教程[M]. 北京：清华大学出版社，北京交通大学出版社，2012，8.