基于复杂网络理论的内河航道网络脆弱性

黄常海， 高德毅,2， 肖英杰， 吴华锋， 彭 宇， 白响恩

(1. 上海海事大学 商船学院, 上海 201306; 2. 上海市教育委员会 办公室， 上海 200003)

基于复杂网络理论的内河航道网络脆弱性

黄常海1， 高德毅1,2， 肖英杰1， 吴华锋1， 彭 宇1， 白响恩1

(1. 上海海事大学 商船学院, 上海 201306; 2. 上海市教育委员会 办公室， 上海 200003)

为掌握内河航道网络特性，提高航道网络维护的针对性和内河航运事故的应急处理能力，缓解突发事件对航道网络造成的不利影响，引入复杂网络理论，对内河航道网络进行研究。基于原始法和对偶法建立内河航道网络模型，对该模型进行网络特性分析，获取航道网的网络特性信息，并对内河航道网络在受到蓄意或随机攻击时网络结构的变化规律进行仿真。以上海市内河航道网为例进行计算，结果表明，基于原始法和基于对偶法的网络模型均具有随机网络特征，基于原始法的航道网络模型在随机攻击情况下，瘫痪前承受攻击的次数约为蓄意攻击下的2倍，蓄意攻击下的脆弱性更为明显；基于对偶法的网络模型在蓄意攻击与随机攻击情况下有更为接近的网络变化性状，两种攻击情况下的脆弱性相似，但蓄意攻击情况下网络变化和瘫痪更为提前。计算结果对上海市航道网络的管理、规划、应急准备具有重要的参考意义。

水路运输； 复杂网络； 内河航道网络； 脆弱性分析； 随机网络

内河水运作为综合运输体系的重要组成部分，在我国的交通运输和国防建设中具有重要地位。对内河航道网络特性进行研究，从内河航道网络的管理和规划角度看，具有重要的现实意义。

在交通运输领域，基于复杂网络理论研究交通运输网络的实例较多，文献[1]基于复杂网络理论对北京市轨道交通运营网络和规划网络进行了对比研究。文献[2]基于复杂网络构建了3种网络模型,以兰州市公交网络为例进行了仿真计算。文献[3]应用复杂网络理论对3座城市公交网络的典型特征进行了分析研究。文献[4]利用复杂网络理论探讨了轨道线网的可靠性,采用Space L方法对广州轨道交通网络进行了拓扑建模,并重点研究了换乘车站故障情况下整个轨道交通网络的受影响程度及可靠性。文献[5]以重庆市轨道交通网络为例，分析了网络的拓扑特征和脆弱性。文献[6]将复杂网络相关理论方法引到了城市燃气输配系统失效因素的分析中。文献[7]以复杂网络理论为基础,分析了海运网络的拓扑结构，验证了海运网络具有小世界和无标度网络特征。文献[8]利用复杂网络理论对班轮航运网络的拓扑特性进行了统计分析。

以上研究主要涉及公交、城市轨道、铁路、管道、海运等交通运输网络，对内河网络的研究并不多。文献[9]把上海内河航运网简化成网络结构图，采用Dijkstra算法计算出各节点到目的港区的最短途径，修正运输途径以得出航运系统比较满意的内河运输集疏运网络方案。可见，尚缺少内河航道网络基本特性、网络脆弱性方面的研究。

在分析上海市内河航道网现状的基础上，分别基于原始法和对偶法构建上海市内河航道网络拓扑模型，对航道网络的平均路径长度、节点度的分布、平均聚类系数等基本特性进行统计分析，并对航道网络遭受随机攻击、蓄意攻击2种不同攻击情况下的脆弱性进行仿真研究。

1 基于复杂网络理论的内河航道网络脆弱性分析

1.1复杂网络基本理论

在网络理论的研究中，复杂网络是由数量巨大的节点和节点之间错综复杂的关系共同构成的网络结构,用数学的语言来说，就是一个有着足够复杂的拓扑结构特征的图。近年来，人们在刻画复杂网络结构的统计特性上提出了许多概念和方法，有3个基本概念：平均路径长度(Average Path Length)、聚类系数(Clustering Coefficient)和度分布(Degree Distribution)[10]。

1.1.1平均路径长度

网络中节点i与j之间的距离dij定义为连接这2个节点的最短路径的边数，网络中任意2个节点之间的距离的最大值称为网络的直径(Diameter)，记为D，即

(1)

网络的平均路径长度L定义为任意2个节点之间的距离的平均值，即

(2)

式(2)中：N为网络节点数。

1.1.2聚类系数

聚类系数用于描述网络中节点的邻点之间也互为邻点的比例，即小集团结构的完美程度。

通常假设网络中的某个节点i有ki条边与邻居节点相连。记这ki个节点之间实际存在的边数Ei与总的可能的边数ki(ki-1)/2的比值为节点i的聚类系数，即

Ci=2Ei/[ki(ki-1)]

(3)

(4)

式(4)中:n为网络的节点总数[5]。

1.1.3度分布

节点i的度ki定义为与该节点连接的其他节点的数目。有向网络中一个节点的度分为出度(out-degree)和入度(in-degree)。节点的出度是指从该节点指向其他节点的边的数目，节点的入度是指从其他节点指向该节点的边的数目。网络中所有节点i的度ki的平均值称为网络的(节点)平均度，记为〈k〉。网络中节点度的分布情况可用分布函数P(k)来描述,P(k)表示一个随机选定的节点的度恰好为k的概率。

1.2内河航道网络模型的构建

描述交通网络主要有2种方法[11]。

1) 原始法(Primal Approach)：将交通网络中的节点(如交叉口、站点等)抽象为图论中的顶点，将节点之间的连接线(如路段、航段等)抽象为图论中的边。

2) 对偶法(Dual Approach)：将交通网络中的线状设施(路段、航段等)抽象为图论中的顶点，将这些线状设施的衔接关系(道路交叉点、公交换乘站、航道交叉口等)抽象为图论中的边。

1.2.1基于原始法的内河航道网络模型构建

在构建内河航道网络模型时，将每条航道与辖区边界的交点及航道间的交叉口视为节点，若节点间可通过航道连接，则将该航道(航段)视为边。

1.2.2基于对偶法的内河航道网络模型构建

水路运输不同于公路运输，运输线路的自我恢复能力较差，跨航道桥梁的坍塌、沉船事故的发生、航道淤积造成的船舶搁浅事故等都可能造成航线崩溃。因此，尝试将各航道(航段)视为航道网络中的节点，将航道之间的交叉或交汇视为航道间的连线，进行内河航道网络模型的构建。

1.3内河航道网络脆弱性分析

网络的脆弱性是指网络中某些节点或边遭受攻击后网络性能下降的程度，可用受攻击后剩余的子网数、最大子网中的节点数或边数进行描述(一般攻击可分为蓄意攻击和随机攻击)。此处所说内河航道网络脆弱性指的是内河航道网络中的节点或边遭受攻击后内河航道网络性能(通航能力)的下降。

对内河航道网络而言，蓄意攻击是指按照航道网络中节点度的大小，从高到低有选择地进行攻击；随机攻击是指随机攻击航道网络中的任一节点。

2 上海市内河航道网络实证研究

2.1上海市内河航道网络结构

2.1.1上海市内河航道现状

上海市内河航道发展的总体框架为“一环十射”,其中:“一环”为黄浦江、大浦线、赵家沟、蕰藻

浜和油墩港组成的环线；“十射”为苏申内港线、龙泉港、苏申外港线、金汇港、太浦河、大芦线、杭申线、川杨河、平申线、罗蕰河。

2.1.2基于原始法的上海航道网络拓扑模型

基于原始法构建上海内河航道网络拓扑模型，见图1。

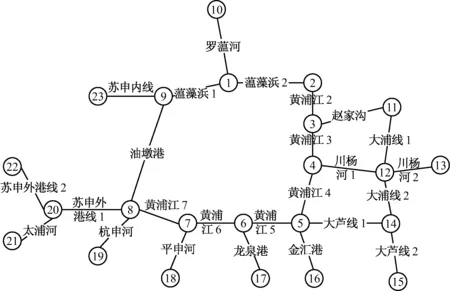
图1 基于原始法的上海航道网络拓扑模型

2.1.3基于对偶法的上海航道网络拓扑模型

基于对偶法构建上海内河航道网络拓扑模型，见图2。

2.2上海市内河航道网络的统计特性及分析

2.2.1基于原始法的上海内河航道网络拓扑模型的统计特性及分析

计算基于原始法的上海内河航道网络拓扑模型

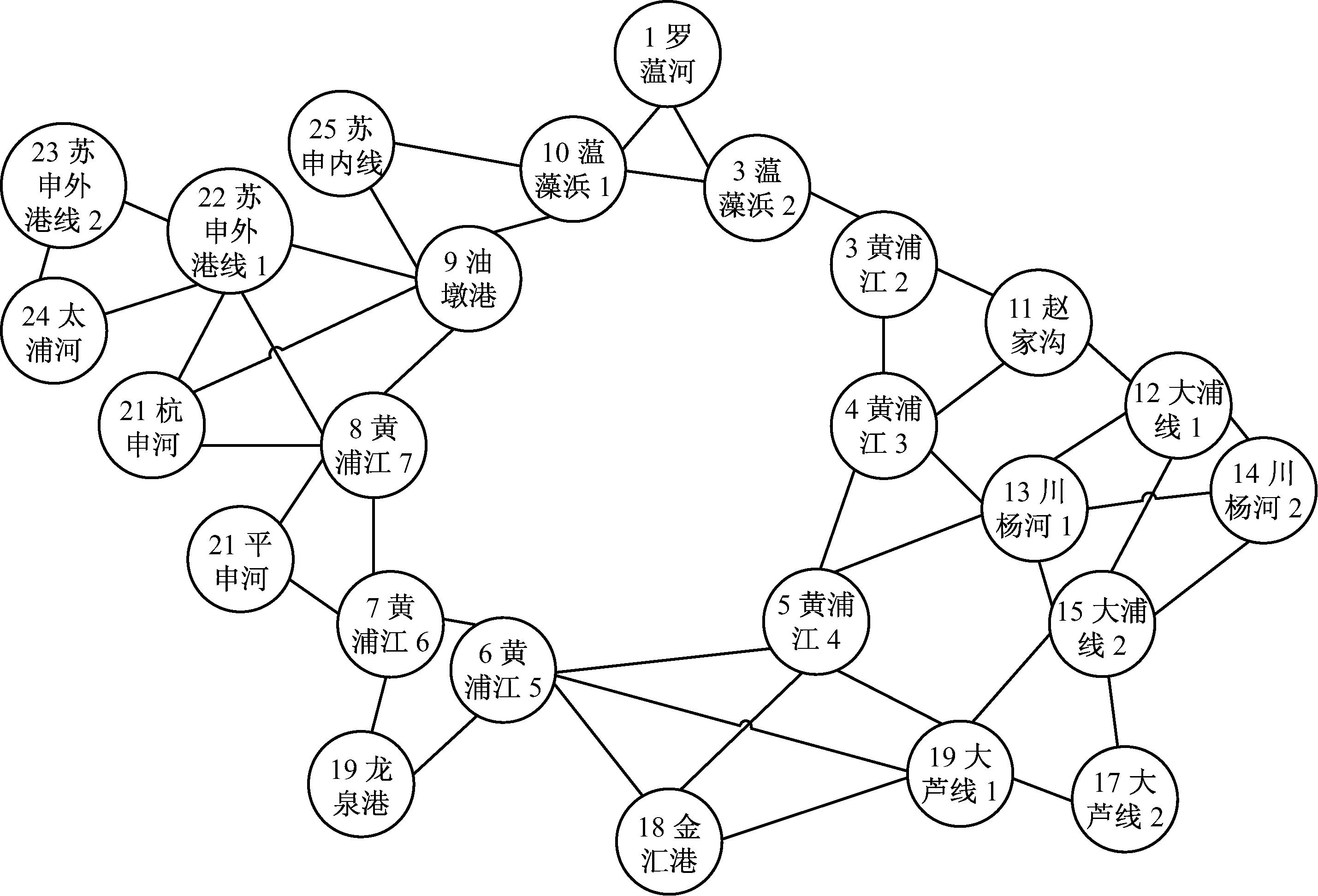
图2 基于对偶法的上海航道网络拓扑模型

的基本统计参数，结果见表1。可以看出，基于原始法的上海内河航道网络拓扑模型共有23个节点和50条边，每节点平均与2.17个节点直接连接，显然上海市内河航道相互间的交叉较少，符合内河航道的特点。平均路径长度为3.74，且聚类系数为0，具有随机网络特征(具有小平均路径长度，但无明显聚类特征)。

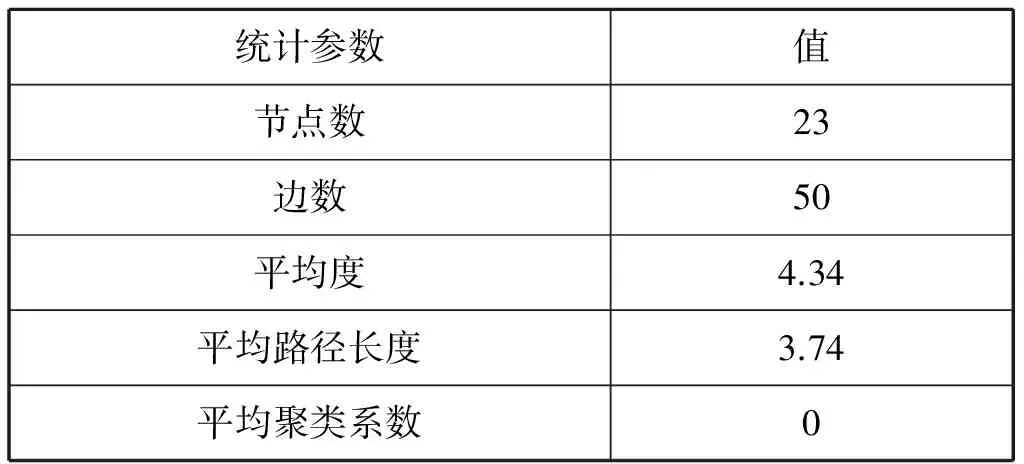
表1 基于原始法的上海市内河航道网络基本统计参数

基于原始法的上海内河航道网络拓扑模型的网络节点度的分布图见图3，部分节点的度统计见表2。

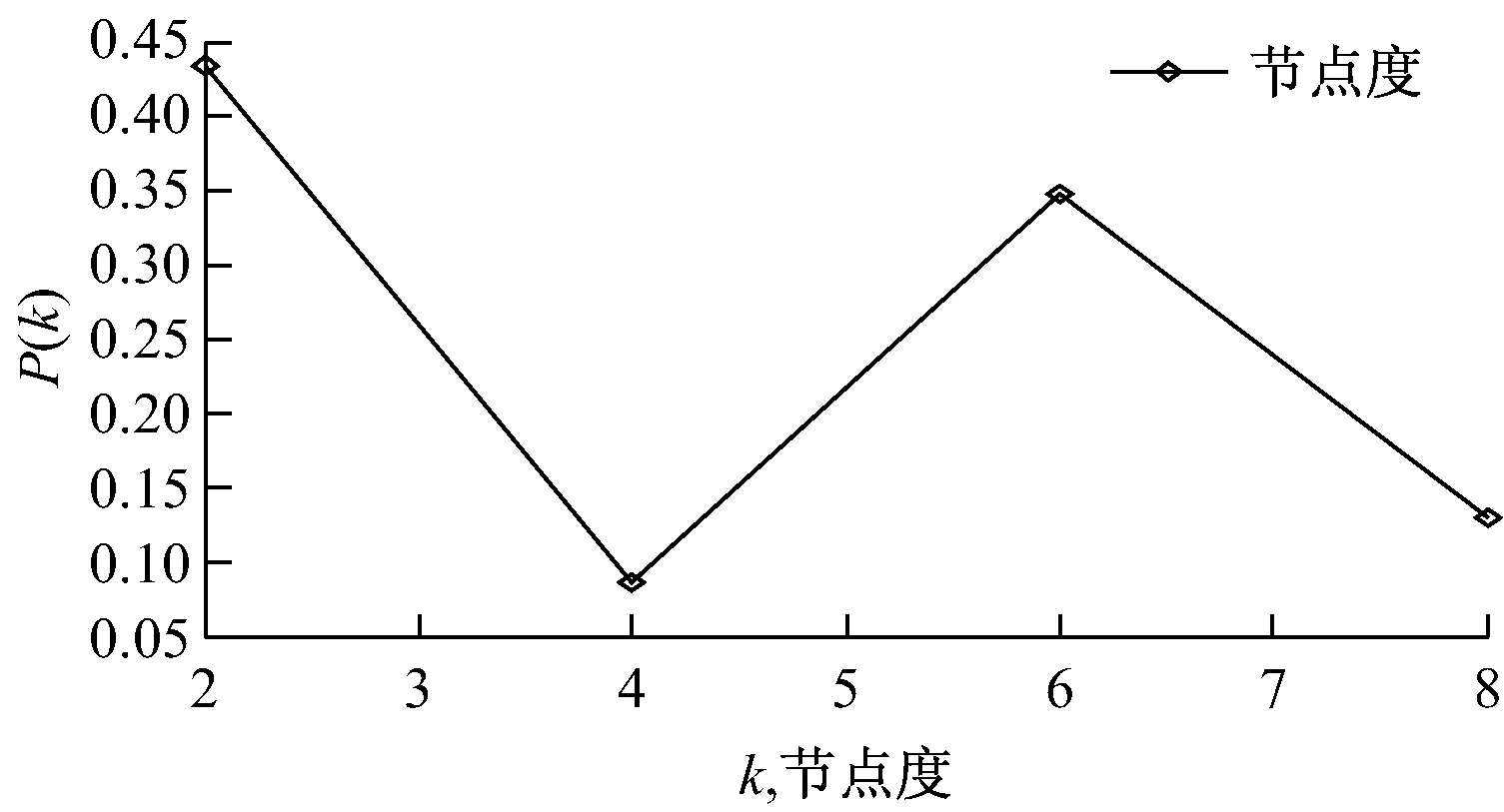
图3 基于原始法的上海市内河航道网络节点度分布

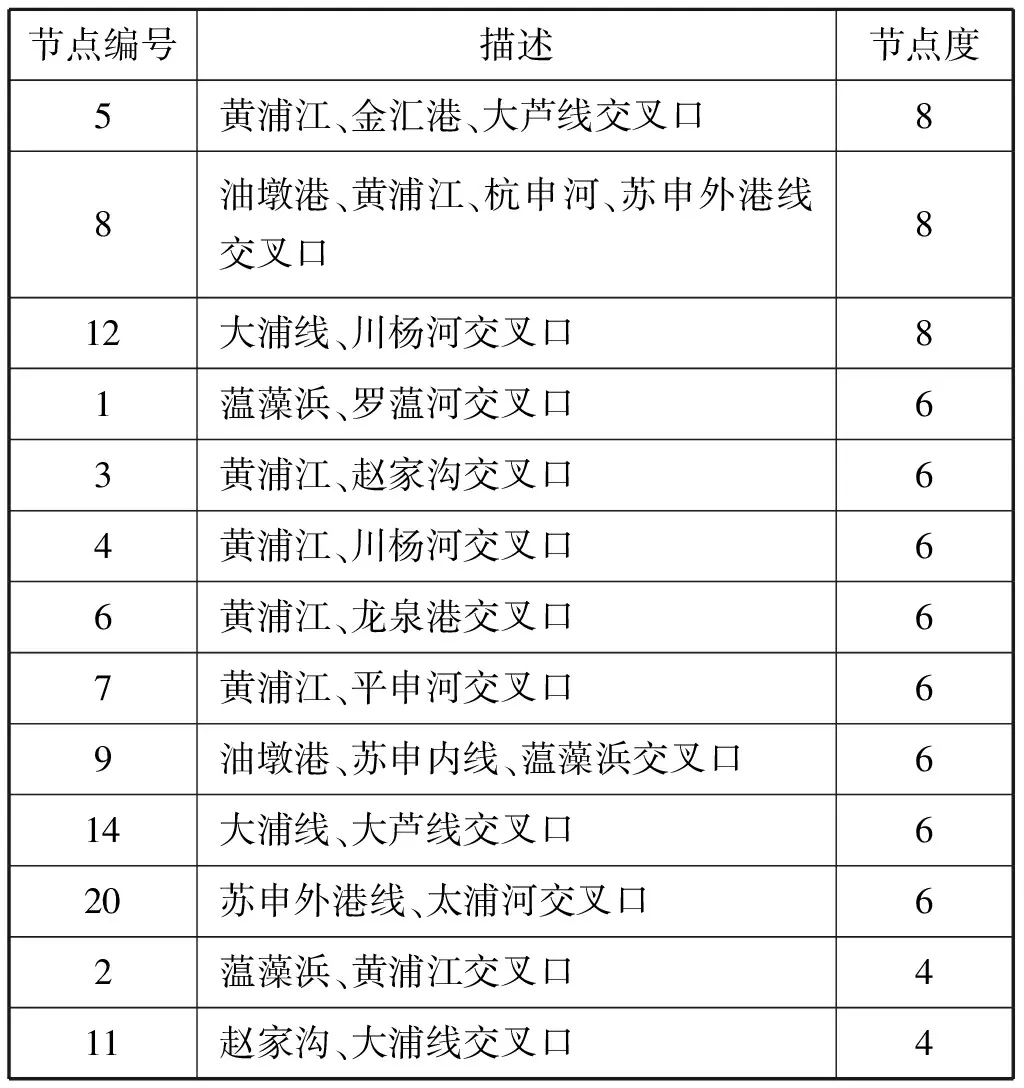
节点编号描述节点度5黄浦江、金汇港、大芦线交叉口88油墩港、黄浦江、杭申河、苏申外港线交叉口812大浦线、川杨河交叉口81蕰藻浜、罗蕰河交叉口63黄浦江、赵家沟交叉口64黄浦江、川杨河交叉口66黄浦江、龙泉港交叉口67黄浦江、平申河交叉口69油墩港、苏申内线、蕰藻浜交叉口614大浦线、大芦线交叉口620苏申外港线、太浦河交叉口62蕰藻浜、黄浦江交叉口411赵家沟、大浦线交叉口4

2.2.2基于对偶法的上海内河航道网络拓扑模型的统计特性及分析

计算基于对偶法的上海内河航道网络拓扑模型的基本统计参数，结果见表3。可以看出，基于对偶法的上海内河航道网络拓扑模型共有25个节点和88条边，每节点平均与3.52个节点直接连接，显然上海市内河航道相互之间的交叉较少，符合内河航道的特点。平均路径长度为3.25，且聚类系数较小，具有随机网络特征。

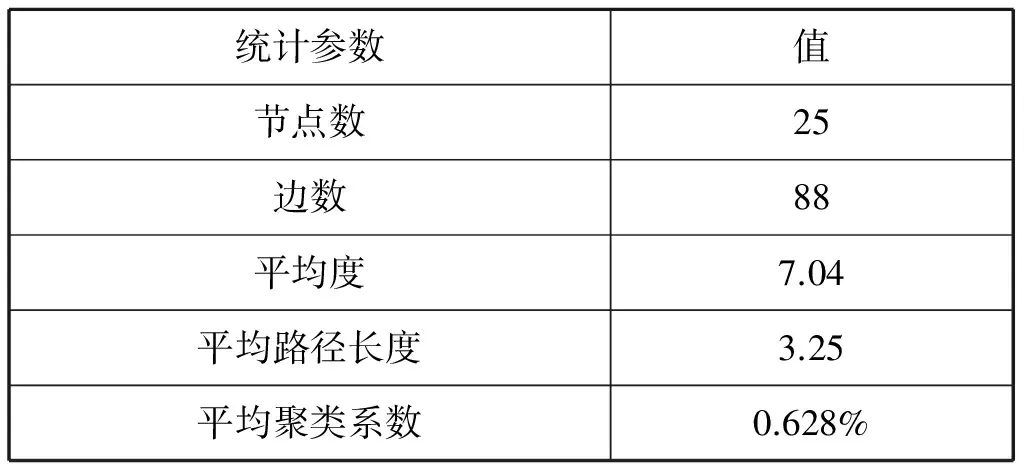
表3 基于对偶法的上海市内河航道网络基本统计参数

基于对偶法的上海内河航道网络拓扑模型的网络节点度分布见图4，部分节点的度统计见表4。

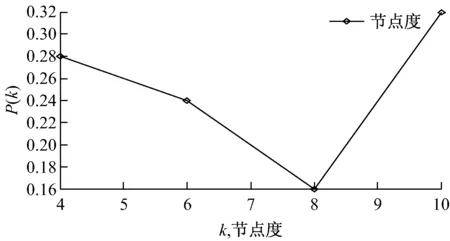
图4 基于对偶法的上海内河航道网络节点度分布

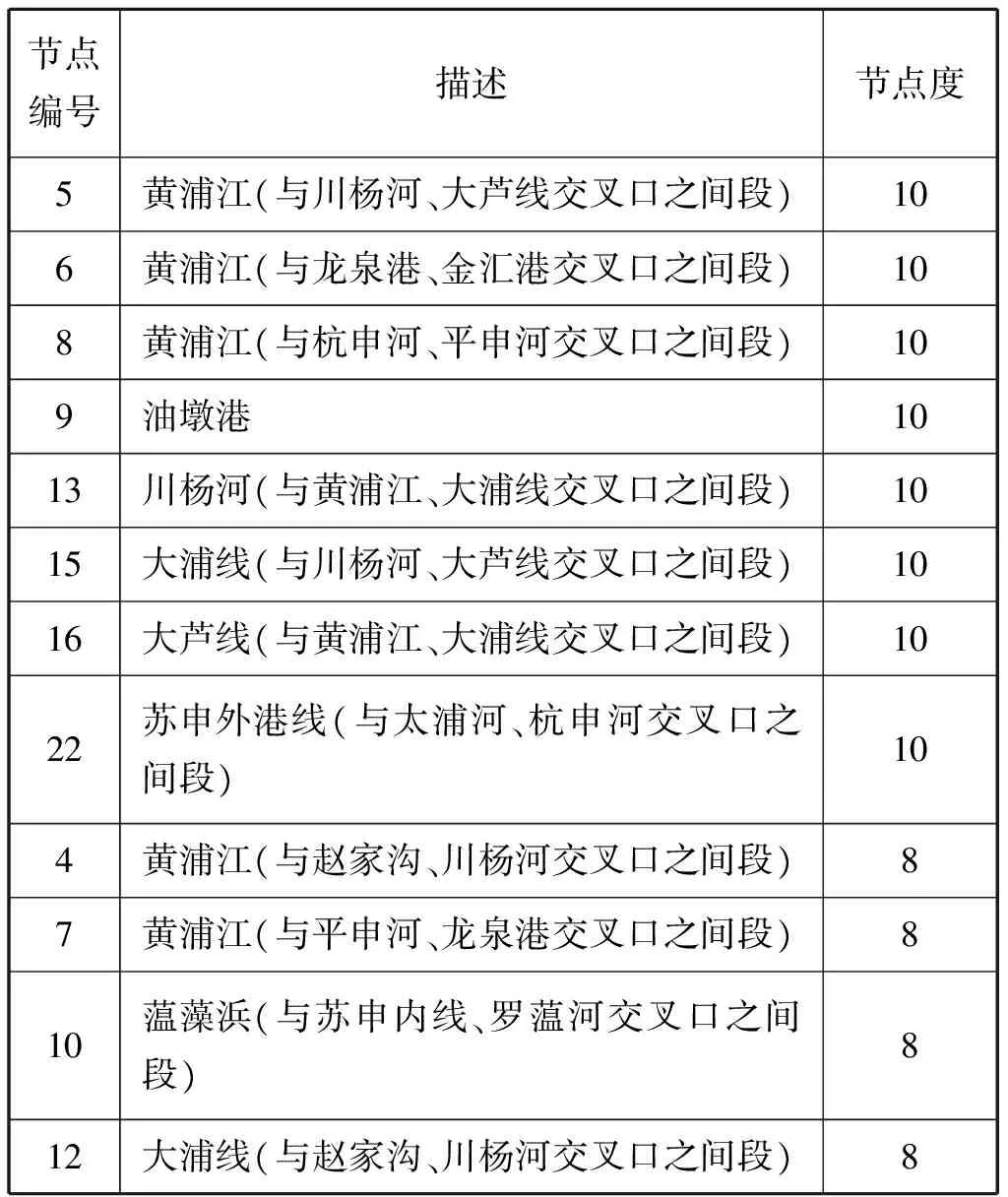
节点编号描述节点度5黄浦江(与川杨河、大芦线交叉口之间段)106黄浦江(与龙泉港、金汇港交叉口之间段)108黄浦江(与杭申河、平申河交叉口之间段)109油墩港1013川杨河(与黄浦江、大浦线交叉口之间段)1015大浦线(与川杨河、大芦线交叉口之间段)1016大芦线(与黄浦江、大浦线交叉口之间段)1022苏申外港线(与太浦河、杭申河交叉口之间段)104黄浦江(与赵家沟、川杨河交叉口之间段)87黄浦江(与平申河、龙泉港交叉口之间段)810蕰藻浜(与苏申内线、罗蕰河交叉口之间段)812大浦线(与赵家沟、川杨河交叉口之间段)8

2.3随机攻击、蓄意攻击情况下上海市内河航道网络脆弱性分析

2.3.1基于原始法的航道网络模型脆弱性分析

2.3.1.1 攻击后网络的节点数和边数

图5和图6中的节点数、边数为整个网络中剩余的节点数与边数，即所有子网的节点数与边数之和。可以看出，蓄意攻击和随机攻击情况下，网络的节点数、边数逐步减少，但蓄意攻击情况下网络节点数、边数减少的速率更快，且很快瘫痪，而随机攻击情况下网络在瘫痪前可经受更多次的攻击。

2.3.1.2 攻击后的子网情况

图7～图9给出了基于原始法的上海市内河航道网络模型在蓄意攻击和随机攻击下剩余子网络特性的变化规律。

从图7中可以看出:蓄意攻击情况下，最大子网的节点数在攻击初始阶段迅速减小;而随机攻击情况下，最大子网的节点数逐步减少。显然，在初始阶段，蓄意攻击情况下最大子网节点数减小的速度大于随机攻击的情况，且蓄意攻击情况下，在不到50%的网络节点被攻击后网络即已崩溃；而随机攻击情况下，在近80%的网络节点被攻击后网络才彻底瘫痪。

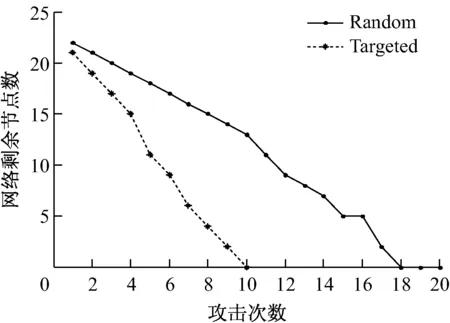
图5 网络剩余节点数

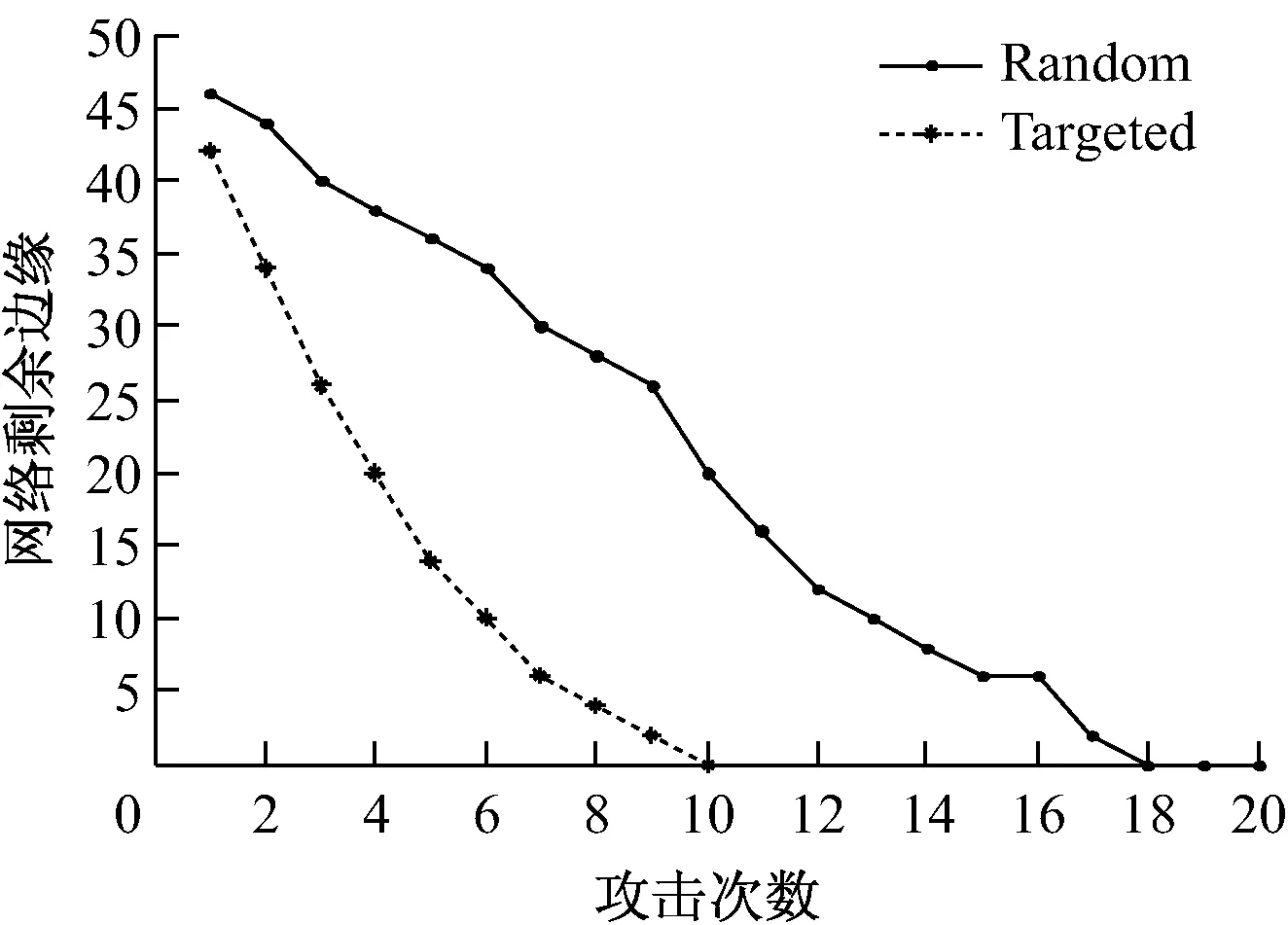
图6 网络剩余边数

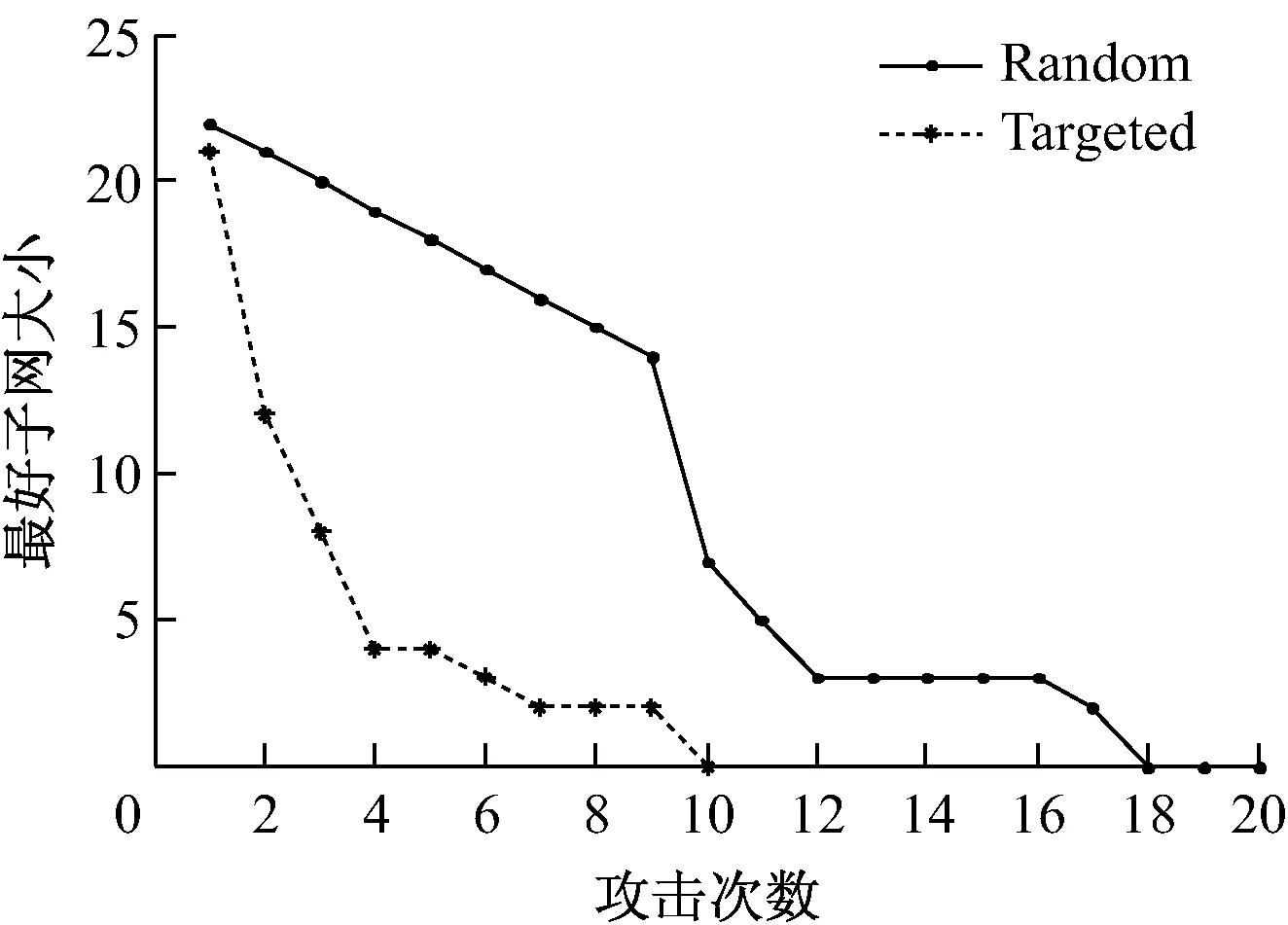
图7 最大子网的大小

图8 剩余子网数目

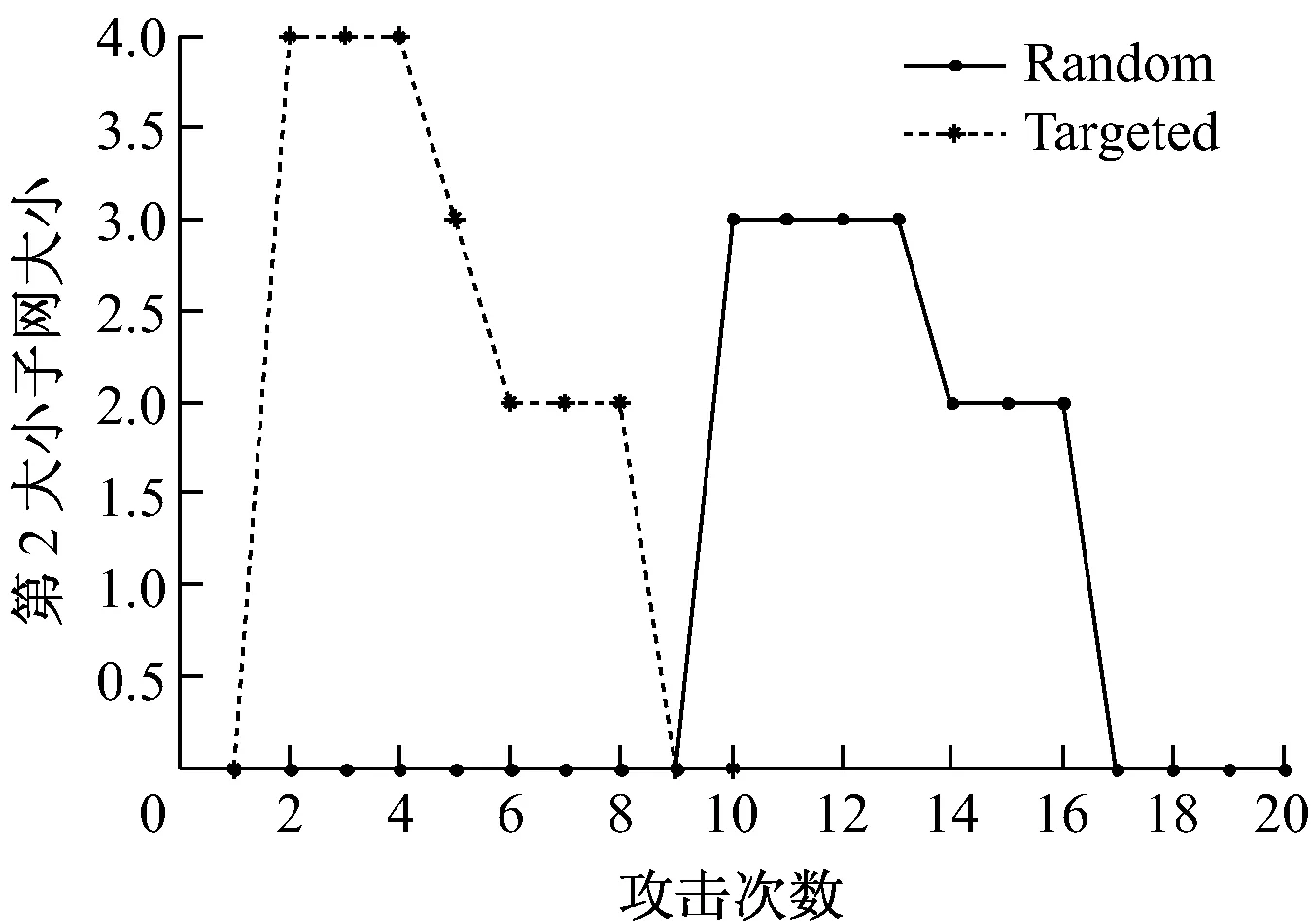
图9 剩余第2大子网大小

从图8中可以看出，在蓄意攻击情况下，剩余子网数随攻击节点的增加而迅速增加，到顶点后又迅速下降。这主要是因为蓄意攻击情况下，整个航道网被分割成多个航道子网络，随着蓄意攻击的进行最后整个网络崩溃。在随机攻击情况下，剩余子网数一度保持为1，也就意味着随机攻击的开始阶段并没有对整个网络构成很大的威胁，随着攻击持续进行，近50%节点瘫痪后，网络也被分割成多个子网，随着各子网的瘫痪，整个网络崩溃。

从图9中可以看出，在蓄意攻击情况下，因整个航道网络被迅速分割，第2大子网迅速形成，但相比整个网络，节点数较少，这意味着第2大子网相对整个网络而言规模较小。而随机攻击情况下，直到近50%节点被攻陷后才出现第2大子网，而后瘫痪。

2.3.2基于对偶法的航道网络模型脆弱性分析

2.3.2.1 攻击后网络的节点数和边数

图10和图11中的节点数、边数为整个网络中剩余的节点数和边数，即所有子网的节点数与边数之和。可以看出，蓄意攻击和随机攻击情况下网络的节点数、边数逐步减少，但蓄意攻击情况下，网络节点数、边数减少的速率更快，而且很快瘫痪；而随机攻击情况下，网络在瘫痪前可经受更多次数的攻击。

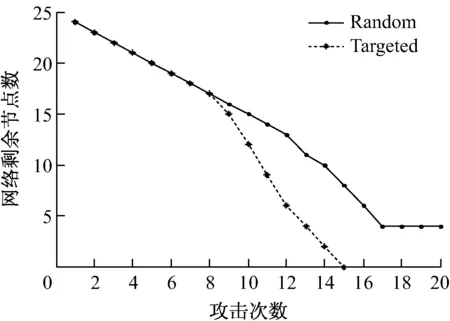
图10 网络剩余节点数

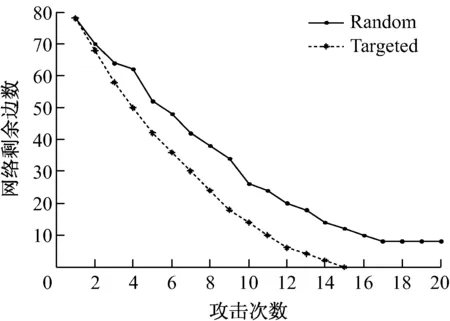
图11 网络剩余边数

2.3.2.2 攻击后的子网情况

图12～图14给出了上海市内河航道网络在蓄意攻击和随机攻击下剩余子网络特性的变化规律。

从图12中可以看出，在蓄意攻击情况下，攻击的初始阶段最大子网的节点数迅速减小，但攻击后期节点数减小的速率趋缓，在网络中近75%的节点被攻击后才瘫痪。在随机攻击情况下，节点数减少速率的波动趋势更明显，且在整个攻击过程中，减小趋势明显大于蓄意攻击情况。

从图13中可以看出，在蓄意攻击情况下，剩余子网数随攻击节点的增加而逐渐增加，到顶点后又逐步下降到0，这是因为在蓄意攻击情况下，整个航道网被分割成多个航道子网络，随着蓄意攻击的进行，最后整个网络崩溃。在随机攻击情况下，剩余子网数攻击开始的前几步保持为1，剩余子网数随攻击节点的增加而增加，到顶点后又逐步下降，攻击后期保持为1。这就意味着随机攻击的开始阶段并没有对整个网络构成很大的威胁，随着攻击持续进行，网络被分割成多个子网，在攻陷60%的网络节点后，各子网随攻击的继续而逐个瘫痪，最后整个网络崩溃。

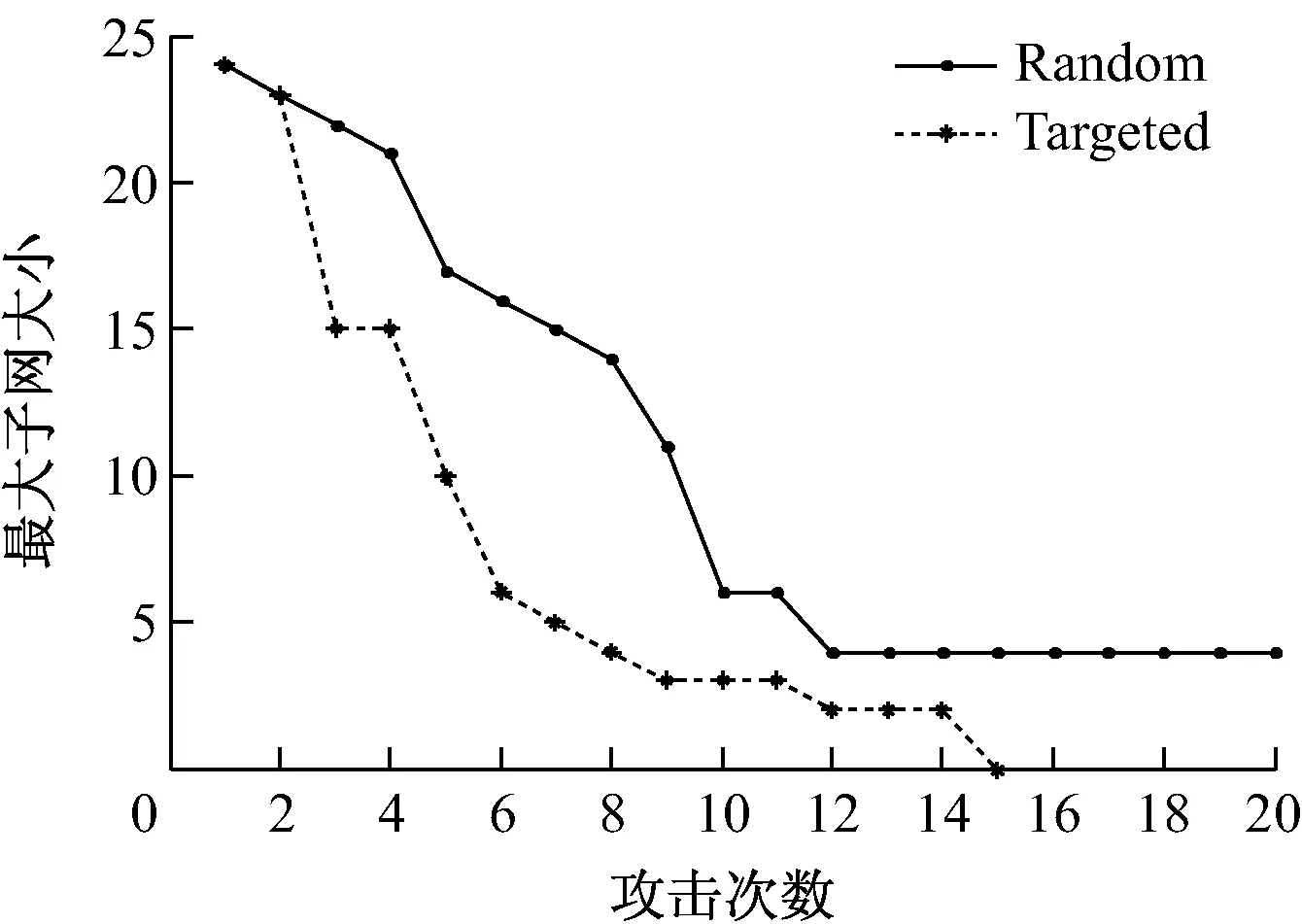
图12 最大子网的大小

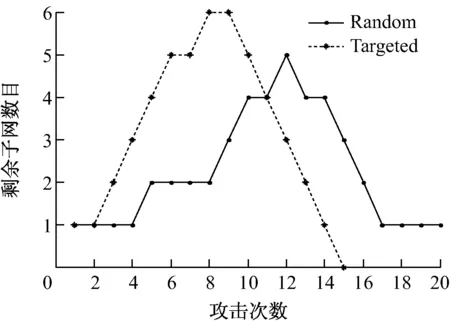
图13 剩余子网数目

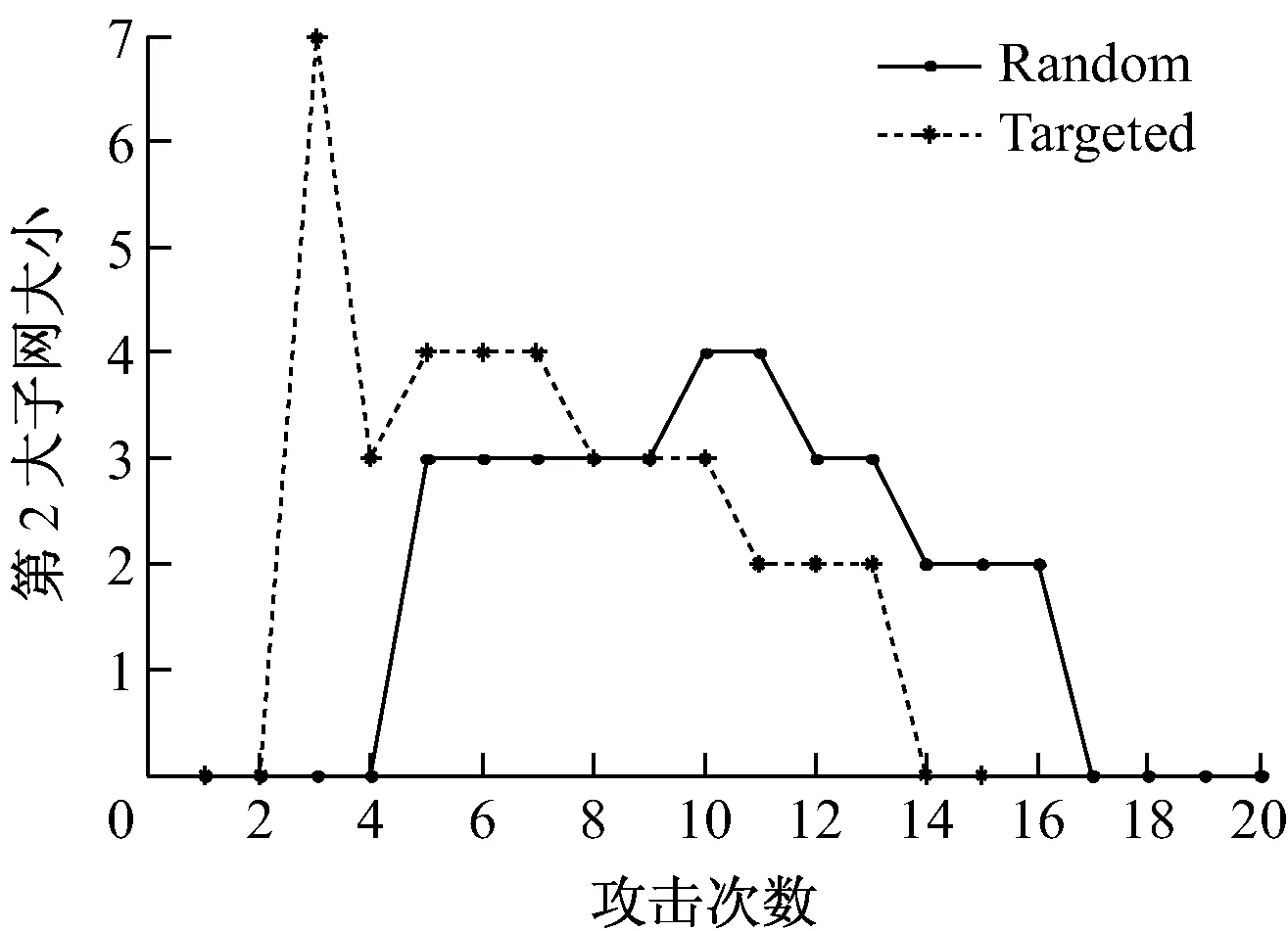
图14 剩余第2大子网大小

从图14中可以看出，在蓄意攻击情况下，10%的网络节点被攻陷后，因整个航道网络即被迅速分割，第2大子网随之形成，规模约为整个航道网络的1/3。随着更多节点被攻陷，第2大子网的规模迅速减小，在减小过程中出现了波动，这主要因为最大子网在攻击中可以被分割成多个子网，第2大子网不是固定的。在整个网络中的70%的节点被攻陷后，第2大子网瘫痪。而在随机攻击情况下，近25%节点被攻陷后也出现第2大子网，规模较小，在80%节点被攻陷后，第2大子网也随之瘫痪。

3 结 语

1. 应用复杂网络理论分析内河航道网络特性，分别建立了基于原始法和对偶法的上海市内河航道网络拓扑模型图。

2. 对基于原始法的上海市内河航道网络拓扑图和基于对偶法的上海市内河航道网络拓扑图的基本特征进行了复杂网络的统计特性分析。基于2种建模方法构建的上海市内河航道网络模型分析结果显示，2种网络模型都有明显的随机网络特征。

3. 对上海市内河航道网络的脆弱性进行了仿真研究，对比了随机攻击、蓄意攻击情况下航道网络的变化情况。基于原始法的网络模型：蓄意攻击情况下，网络表现出明显的脆弱性，网络很快被分割成多个子网，并很快瘫痪；而随机攻击情况下，网络在瘫痪前承受攻击的次数约为蓄意攻击下的2倍。基于对偶法的网络模型：蓄意攻击情况下与随机攻击情况下网络的变化趋势更为接近，网络脆弱性相似，但随机攻击情况下网络的变化比蓄意攻击滞后。

4. 上海市内河航道网络基本特征统计分析、网络脆弱性仿真结果对内河航道的管理和维护、未来内河航道的规划和建设具有重要参考价值。

5. 对于不同通航标准、不同航道里程对内河航道网络的影响,有待做进一步研究。

[1] QIAO Ke, ZHAO Peng, YAO Xiangming. Performance Analysis of Urban Rail Transit Network[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(4):115-121.

[2] 赵山春. 基于复杂网络理论的城市公交网络可靠性研究[J]. 中国安全科学学报,2013,23(4):108-112.

[3] LU Huapu, SHI Ye. Complexity of Public Transport Networks[J]. Tsinghua Science amp; Technology, 2007, 12(2): 204-213.

[4] 刘志谦,宋瑞. 基于复杂网络理论的广州轨道交通网络可靠性研究[J]. 交通运输系统工程与信息,2010,10(5):194-200.

[5] 叶青. 基于复杂网络理论的轨道交通网络脆弱性分析[J]. 中国安全科学学报,2012,22(2):122-126.

[6] 高鲁彬,郭进利. 基于复杂网络的城市燃气输配系统失效因素分析[J]. 中国安全科学学报,2010,22(6):111-115.

[7] 王杰,李雪. 基于改进BA模型的海运复杂网络演化研究[J]. 武汉理工大学学报:交通科学与工程版,2013,37(3):496-500.

[8] 牟向伟,陈燕,杨明,等. 班轮航运网络拓扑特性[J]. 大连海事大学学报,2009,35(2):34-37.

[9] 陈飞儿,张仁颐. 上海港集装箱内河集疏运网络优化[J]. 上海交通大学学报,2006,40(6):1019-1023.

[10] 汪小帆,李翔,陈关荣. 复杂网络理论及其应用[M]. 北京：清华大学出版社,2006:9-46.

[11] PORTA Sergio, CRUCITTI Paolo, LATORA Vito. The Network Analysis of Urban Streets: A Dual Approach[J]. Physica A: Statistical Mechanics and Its Applications, 2006, 369(2): 853-866.

VulnerabilityofInlandWaterwayNetworkfromAngleofComplexNetworkTheory

HUANGChanghai1，GAODeyi1,2，XIAOYingjie1，WUHuafeng1，PENGYu1，BAIXiang'en1

(1. Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China； 2. Administrative Office, Shanghai Municipal Education Commission, Shanghai 200003, China)

The complex network theory is introduced to study the characteristics of the inland waterway network, which is necessary for strengthening the pertinence of maintenance of the waterway network, improving emergency response capabilities and mitigating the adverse impact of unexpected events on the waterway network. The primal approach and the dual approach are used to model the inland waterway network, and the network characteristics of the waterway network is studied with the models. The variations of Shanghai inland waterway network structure under random attacks or intentional attacks are studied through simulation. The simulation indicates that both primal approach and dual approach models of the inland waterway network possess random network characteristics, and the primal approach network model can bear random attack as twice times as intentional attacks before collapse, meaning that it is more vulnerable to intentional attacks. On the other hand, the dual approach network model shows similar response characteristics and similar vulnerability to random attacks and intentional attacks, though intentional attacks makes the network collapses slightly early. The study can be a guide to management, planning, emergency preparedness of Shanghai waterway network.

waterway transportation; complex network; inland waterway network; vulnerability study; random network

2014-08-24

国家自然科学基金(51279099);上海曙光计划(12SG40);上海海事大学研究生创新基金(yc2012067);上海海事大学优秀博士学位论文培育项目(2013bxlp006)

黄常海(1987—)，男，山东滕州人，博士生，主要从事水上交通安全管理、海上搜救无线传感网等方面的研究。

E-mail:changhai406@126.com

高德毅(1958—)，男，浙江绍兴人，教授,博士生导师，主要从事海事政策与法规、安全管理、船员管理、航海教育与管理等领域的研究。E-mail:gaodeyi@shmtu.edu.cn

1000-4653(2014)04-0044-06

U612, X913

A