无刷直流电机单神经元自适应智能调速系统

魏巍WEI Wei

（大庆炼化公司电子商务部，大庆 163310）

（Daqing Refining &Chemical Company E-commerce Department，Daqing 163310，China）

0 引言

目前无刷直流电机（BLDCM）被广泛应用，是因为它有许多优点，像：本身体积较小、功率密度较其他电机高、相对控制要简单、动态性能较好。由于它的控制系统特点是非线性且多变量的，所以利用传统的PID 控制算法达不到电机的高精度要求和运行；而对于像滑膜变结构、神经网络及模糊控制等先进的控制算法实现起来更复杂。

本文在建立无刷直流电机双环调速系统时采用单神经元自适应控制方法，在调节神经网络参数上应用Hebb学习规则，同时此电机的反电势应用分段线性法模拟其变化趋势。由此搭建了双闭环BLDCM 智能调速系统，仿真结果得出了此系统较其他系统抗干扰能力更强，有较强的随动性。

1 无刷直流电机建模策略

全控桥式三相星型无刷直流电动机结构如图1 所示[1][2]。每相的定子绕组与其相对应的电子开关线路中的功率开关器件相连。此结构类似一个“电动机系统”，其系统相当于是由电子开关线路、永磁式同步电机和位置传感器构成的。

图1 三相星型全控桥式BLDCM 结构图

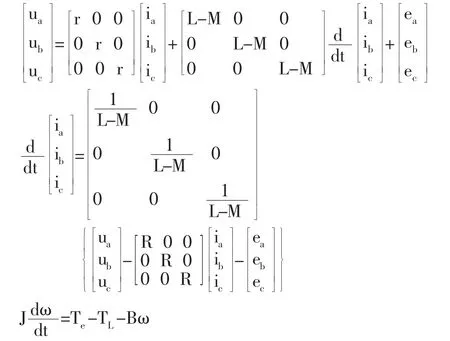
根据BLDCM 三相绕组的电压平衡方程、运动方程和状态方程，建立BLDCM 电机本体仿真模型如图2 所示。

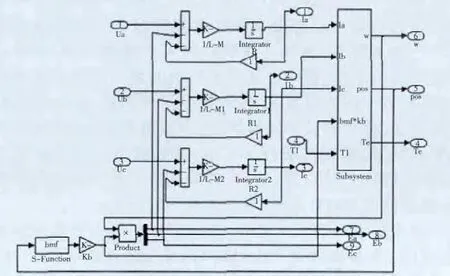
图2 BLDCM 本体结构建模

本文采用工作方式是每一瞬间有两个功率管导通的梯形波电枢驱动电流。再应用分段线性法模拟梯形波的反电势波形趋势，通过将转子的位置信号作为划分运行周期的依据，把周期化为6 个阶段，见图3，以第一阶段（0～π/3）为例：A 相反电势为正向最大值Em，B 相为反向最大值-Em，而C 相则在换相阶段。通过两个信号变量分别是转子位置和转速信号来列出每一相反电势变化趋势的轨迹方程。

图3 星形两相导通六状态BLDCM 反电动势波形

表1 列出了转子位置和反电动势两者之间的线性关系，k 为反电动势系数；pos 为电角度信号；w 为转速信号。

表1 转子位置和反电动势之间的关系表

2 控制策略与控制方法

利用滞环控制调节系统内环的电流，如图4 所示，当系统反馈的瞬时电流值与设定的电流值做减法运算得到的数值等于滞环环宽的正向边界时，VT1导通，VT4关断，此时电动机与直流母线的正端接通，电流升高，相反的电流下降。为了实现实际电流跟踪参考电流波形形成闭环控制，滞环的宽度选择很重要。

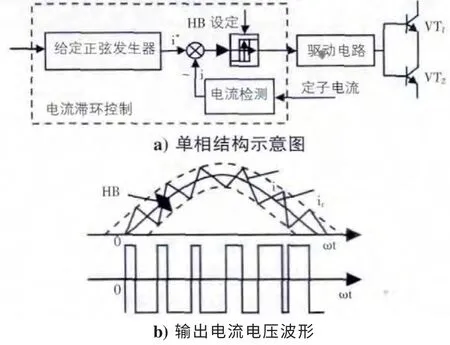
这里用单神经元自适应PID 控制系统外环[3][4]，图5 为其结构图，系统误差、一级差分以及误差累积做为单神经元的输入量。

神经元通过关联搜索，计算产生输出信号u(k)为

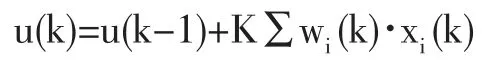
K 为调节环节放大系数，K 值过大会威胁系统的稳定性，而K 值过小，又会使降低系统的快速性，可见，K 值的选择非常重要。本系统K 取值为2。

wi(k)为权系数，用Hebb 学习规则调整权系数，在线实时整定PID 控制的三个参数。

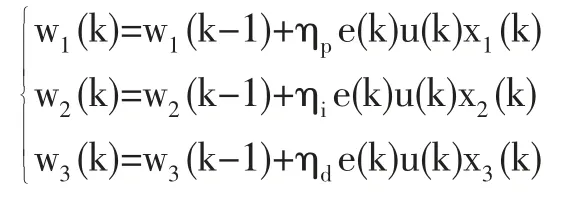
如果要分别调整不同的权系数就要用不同的学习速率，比例、积分、微分的学习速率分别用ηi、ηp、ηd表示。在每次采样的同时都要依据反馈的误差来对神经元的权值进行重新调整，本文ηi、ηp、ηd取为0.35，0.50，0.35；三个初始权值取0～1 之间的随机数。

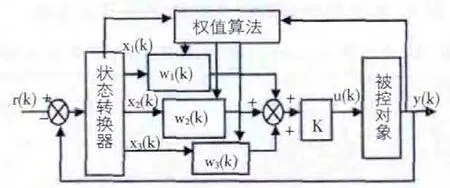
图5 单神经元控制结构图

由于e(k)和Δe(k)决定PID 参数的在线学习修正结果，所以想到了把xi(k)改为e(k)+Δe(k) 代入原来的PID 控制算法中的加权系数的学习修正部分，改进结果如下：

式中，Δe(k)=e(k)-e(k-1)。

3 系统建模

综上所述，BLDCM 的控制系统框图如图6 所示。采用双闭环控制方案，其中PI 调节器构成转速环，电流滞环调节器构成电流环。

图6 BLDCM 控制系统设计框图

图7 为系统总体仿真模型图，由BLDCM 本体模块、速度控制模块、参考电流模块、电流滞环控制模块、转矩计算模块和电压逆变器模块构成。

图7 BLDCM 控制系统建模

图8 为滞环控制模块，三相的参考电流和实际电流作为输入量，PWM 逆变器控制信号作为输出量。从参考电流模块那输出三相的参考电流，表2 列出了转子位置和三相参考电流之间的对应关系。

图8 电流滞环控制模块结构框图及其封装

表2 转子位置和三相参考电流之间的对应关系表

本系统采用常规PID 和单神经元自适应PID 两者分别作为速度环控制器构成速度环控制模块。单神经元自适应PID 控制器模型如图9 示。

图9 单神经元自适应PID 控制器模块及其封装

4 系统仿真及实验验证

选择BLDCM 电机参数为：定子相绕组电阻R＝1Ω，定子相绕组自感L＝0.02H，互感M＝-0.061H，转动惯量J=0.005kg·m2，反电势常数Ke=0.185V·s/rad，阻尼系数B=0.0002N·m·s/rad，额定转速n=1000r/min，极对数p ＝1，220V 直流电源供电，峰值电流35A。

系统进行空载启动，达到稳态后，负载TL＝2.5N·m 在t＝0.7s 时加进系统，又在t＝1.4s 时从系统中撤去负载，最后得到三相电流、三相反电动势、转子位置信号和PWM 脉宽调制信号的仿真波形如图10 所示。

结果分析，空载运行时电流为零，电流在加上负载后迅速增加接近稳态，还可以看出方波电流波形的平顶部分因为换向而引起脉动。三相反电势波形平顶部分约为120°。

采用常规PID 和单神经元自适应PID 两者分别作为速度环控制器构成速度环控制模块，转速设定为1000rpm，系统同样空载启动，负载转矩TL＝2.5N·m 在t=1s时加入系统，对比两种不同算法的速度响应仿真曲线波形如图11 所示。从图可知，系统在常规离散PID 控制下，大约用了0.45s 的时间从系统启动到进入稳态，而且有较大的超调量，约为40%；转速在t＝1s 时发生突降，经过控制器的调节作用，大约经过0.35s 后，系统再次恢复到平衡状态。相比之下，应用单神经元自适应PID 控制，系统在很短的时间内就进入到了稳态，超调量远远小于前者，仅为1.5%；转速在t＝1s 时加入负载时只出现了很小的波动，就迅速恢复到平衡状态。

图11 1000rpm 下转速响应曲线

图12 为系统在常规离散PID 和单神经元自适应PID控制下的转矩输出响应曲线。和常规PID 控制相比，单神经元自适应PID 控制下的转矩波动较小。

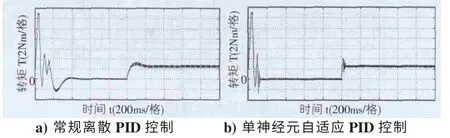
图12 转矩响应曲线

5 结论

本文基于BLDCM 电机建立的单神经元自适应PID智能调速系统具有较强的跟随性、抗扰性和鲁棒性，这些方面都远远优越于常规PID 控制器，单神经元自适应PID控制器之所以具有很强的参数适应性和鲁棒性，动态响应快等优点，是因为它不受系统参数变化的影响，只需要考虑系统的输入和输出的变化就可以。可见，该系统还可以控制一些高性能的调速系统，具有广泛的应用前景。

[1]张琛.直流无刷电动机原理及应用[M].北京:机械工业出版社，2004.

[2]卿启新,叶汉民,杨晓武,时晓霞.基于模糊RBF 神经网络的无刷直流电机调速控制[J].化工自动化及仪表,2010,37（7）：84-86.

[3]付华，冯爱伟，徐耀松等.基于单神经元控制器的异步电动机矢量控制[J].中国电机工程学报，2006，26(1):127-131.

[4]代睿,曹龙汉,何俊强,唐超,刘小丽.基于微粒群算法的无刷直流电机单神经元自适应控制[J].电工技术学报,2011,26(4):57-63,70.