新型可洗井封隔器密封元件受力分析

王岩WANG Yan

（大庆油田有限责任公司第一采油厂生产保障大队，大庆 163311）

（Daqing Oilfield Co.，Ltd.First Oil Production Plant Production Security Team，Daqing 163311，China）

0 引言

众所周知密封元件（即弹性元件）是封隔器的核心部件，密封元件决定着封隔器井下的工作性能。当密封元件井下工作时，其与密封元件材质的好坏、构造的完整程度等因素都有着一定得关系。站在密封元件设计以及使用的角度上，如何使选材合理、设计得当从而操作正确，必须有一个严格的标准来进行约束。由此不难发现，对密封元件进行受力分析是很有必要的，同时还应该对密封元件在井下的工作情况进行全面的分析。近年来，国外等诸多国家在此方面发表了许多不同的学术见解，尤其是前苏联贡献比较大，为封隔器的深远发展提供了一定的理论基础。

本文研究的Y341-114 型封隔器为压缩式封隔器。

1 压缩式密封元件受力分析

1.1 对有“防突”装置的压缩式密封元件进行受力分析“防突”其实就是把某种特定的阻挡环或者其他的限制保护装置放置在密封元件的端部，它的作用是在封隔器坐封时，能够有效地保证密封元件各部件都在正确的位置上，从而得到良好的密封能力。

对接触压力和纵向变形量，关系式为：

1.2 对无“防突”装置的压缩式密封元件受力分析 有的密封元件是没有“防突”装置的，对于这一类的密封元件，式（1）就会存在着一定的局限性。为了消除这个不足，无“防突”结构的胶筒总的接触压力Pk为：

Pkn——工作阶段压差形成的接触压力；

Pkc——初封阶段轴向预压形成的接触压力。

2 对密封元件的参数进行确定

2.1 力学角度分析 要想确定密封元件的参数，对其力学角度的分析是必不可少的一步，首先应该对密封元件进行力学角度分析，然后进行计算操作，我们可以将密封元件外表面与套管壁之间的最大可用间隙以及和密封元件和坐封载荷的高度分两个主要阶段进行分析处理。

2.1.1 从胶筒变形到套管接触 本文假设径向变形是沿着弹性体的整体高度轴对称而又均匀的发生，前提是体积压缩不能够超过弹性限度，对其进行第一近似计算（去掉高阶微分项），如图1 和图2 所示，可以得到微分方程，为：

式中，a=1+εz

解方程（3）得其通解：

值ψ1(z)可以从下列条件求得

r=R0，u=0；则

将ψ1(z)代入方程（4），得

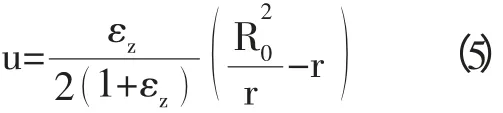
由式（5）就能可以得到弹性元件的外表面与套管壁之间及胶筒经过变形后与当套管壁相互接触时所需要加的轴向载荷之间的最大可用间隙。

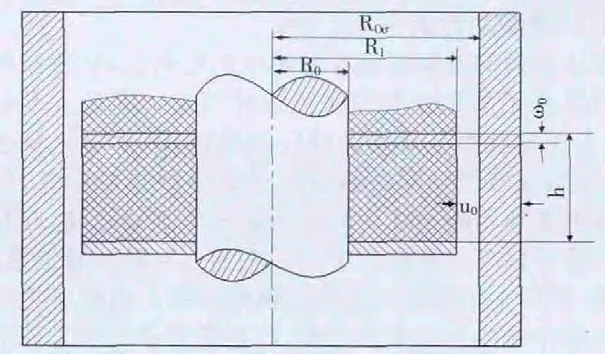
图1 密封元件结构示意图

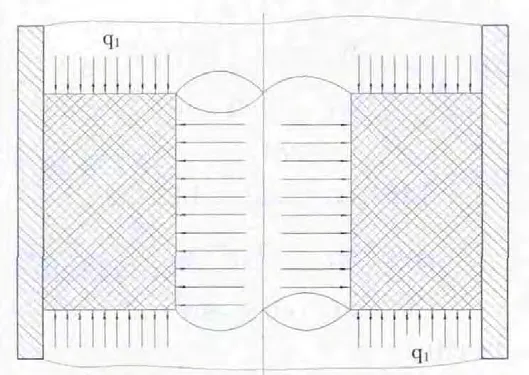
图2 密封元件初封受力图

从边界条件r=R1，u=u0（见图1 和2）得，

为了使密封元件的弹性在给定温度条件下能保持一定时间，必须满足

式中，[ε]——弹性体许用相对轴向变形，用试验方法求得，其大小决定于材质和工作条件。

从（6）和（7）两式求得最大许用间隙为

相应的应力值可按照广义虎克定律求得：

式中，λ——拉梅系数。

从式（3）得，

因为

运用方程（10）-（12）求得，

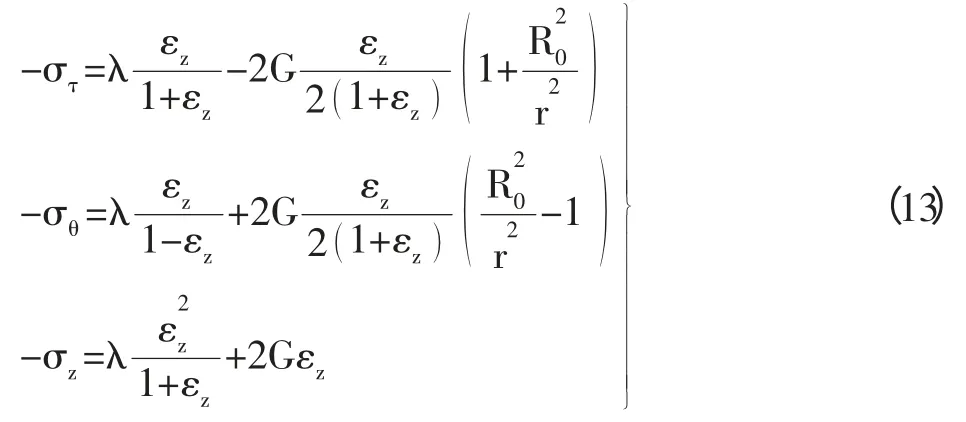
以上所阐述的关于应力的表达式都能够符合弹性力学领域中的平衡联立方程。

2007—2017年世界纸浆进口额排名前5位的国家包括中国、美国、德国、意大利、韩国和日本，2007年依次为中国、美国、德国、意大利和日本，2017年为中国、美国、德国、意大利和韩国。中国始终占据进口额第1位，且世界占比逐渐由2007年的15%上升至2017年的30%;美国和德国分别居第2或第3位，但两者之间差距始终不大而同时在后期与中国差距加大;意大利始终居第4位;除2007和2008年日本占据第5位外，韩国始终位居第5。

我们必须提前确定胶筒与套管之间合适的间隙，因为井下封隔器的起下作业与之密切相关。从而得到这个间隙值，可根据间隙u0=Roσ-R1和弹性体的总体积的绝对不可压缩性求得：

式中，q1——使弹性元件变形到接触套管壁时加在其端面上的比压（单位面积上的载荷）。

2.1.2 元件能够接触套管后 一旦元件可以接触套管后，封隔器中心管和套管的刚度对胶筒变形的情况有着直接的关系，并且由于套管在封隔器坐封阶段是固过水泥的。因此，一般来说，只有胶筒变形的情况没有超过密封元件所能承受的极限，我们可以对胶筒与周向变形以及套管接触后的径向忽略不计。为εr=εθ=0，（见图3）。

图3 密封元件坐封时的受力图

在这种情形时，由式（9）可得

其中q2是在当层间的压差为的情况下，同时若要密封元件达到一定的密封程度，则需要将其加在胶筒端面上的比压（其中Pn和Pk表示为封隔器上、下的压力），胶筒在压差ΔP 作用下为确保密封决定着其大小。我们可以通过试验的方法去进行测得不同尺寸以及结构的胶筒的关系曲线，可表示为：[P]=f(ΔP)。

由公式（15）可知，若要达到密封条件，则必须符合στr=Roσ≥[P]。

由以上分析可知，两个阶段所加的轴向载荷之和构成了单位面积上的轴向坐封载荷（比压）q。根据公式（14）和（15），可得

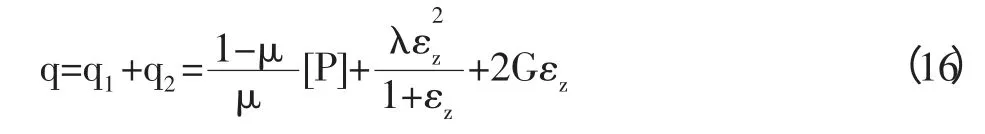
从公式（16）可以看出，压差、胶筒与胶筒的尺寸以及套管的原始间隙决定着密封轴向载荷。

2.2 明确胶筒的高度 若底层在工作时，弹性密封元件会承受着由压差产生一定的剪切效应（见图4 和5）。

图4 剪切效应的示意图（a）

若这种情况发生则会产生一定的剪切应力，我们可以根据下列方程式中求得：

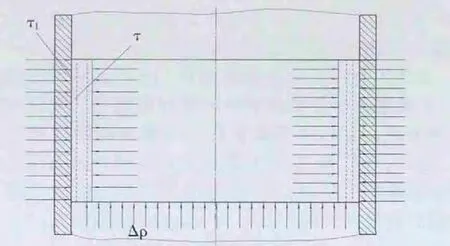
图5 剪切效应的示意图（b）

式中，[τ]——弹性元件可用的剪切应力。

3 Y341-114 型封隔器在井下工作的受力分析

当下我厂所用的Y341-114 型封隔器的具体工作参数如表1 所示。

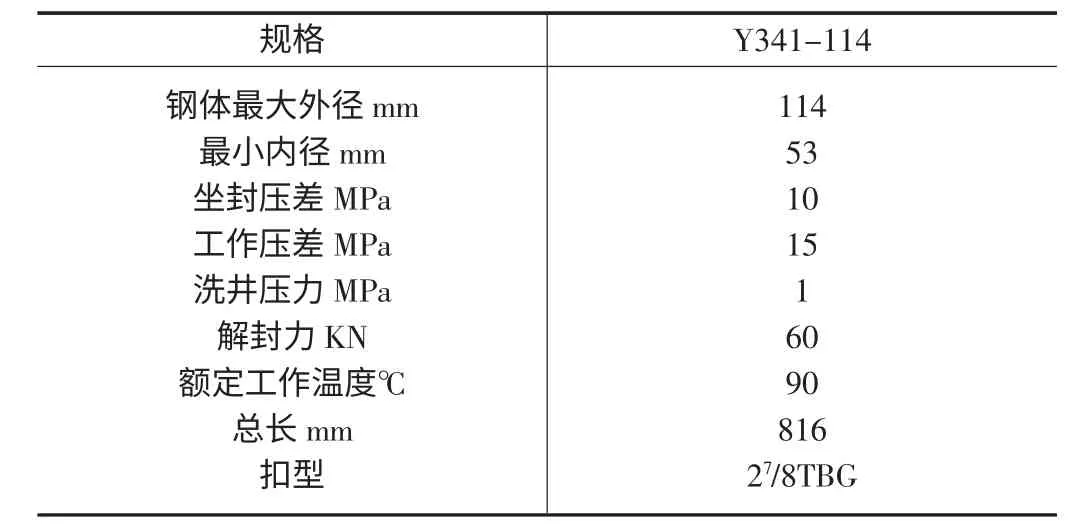
表1 Y341-114 封隔器的具体工作参数表

套管内半径Roσ=60.5mm，密封元件外半径R1=57mm，密封元件内半径Ro=40mm，封隔器中心管外半径rm=40mm，取μ=0.475，G=12.7kg/cm2，橡胶与套管间的摩擦系数f 取0.3。有两个65mm 的胶筒高度，还有一个为55mm。

3.1 坐封力的具体计算情况 首先，坐封力是由结构和工作压差求得，再去参考封隔器的实际工况，要求工作压差不能够应用在中心管界面，所以

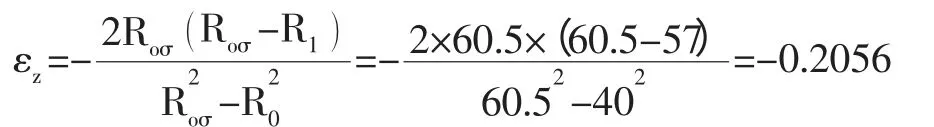
作用于65mm 长胶筒所需坐封力为：

作用于55mm 长胶筒所需坐封力为：

因此，所求得的坐封力总数为7.6 吨。

3.2 接触应力的具体计算情况 当工作压力在15MPa下，当下封隔器在工作过程中产生的接触应力为：

加入我们对此封隔器进行改造，具体表现为增加“防突”型装置，则得到的接触压力为：

由此可知Pk2＜Pk1

综上所述，当处在相同工作压差的情况下，增加“防突”装置具有一定的突破性，能很大的减小胶筒的接触应力，因此我们对当前封隔器进行改进是非常必要的而且很有效果的。

4 结束语

本文主要工作时对封隔器胶筒的坐封整个过程实施有限元分析，从而对有“防突”装置和无“防突”装置这两种情况下胶筒的状态进行了详细的比较。我们分析的结果是若做有限元分析则需要以下两个要点，一是需要用一种典型的非线性材料做胶筒用的橡胶，表现出的特征是弹性和高度非线性，对其进行有限元分析所采用的方法与弹性材料是不一样的，有一定的差异度。二是胶筒与隔环、中心管、套管之间会有一定的接触，对于接触问题来说也是我们常见的典型的非线性问题。由分析可以看出，防突结构有效的降低了胶筒的最大Mises 应力，证明了防突结构设计是合理的。

[1]庄茁，张帆，岑松等.ABAQUS 非线性有限元分析与实例[M].科学出版社，2005.

[2]郑明军，谢基龙.压缩状态下橡胶件大变形有限元分析[J].北方交通大学学报，2001，25（1）：76-77.

[3]李楠.压缩式封隔器胶筒的密封性能研究[D].东北石油大学，2012.