GPS 卫星钟差二次多项式预报模型的总体最小二乘算法

2014-11-28张清鸾ZHANGQingluan魏朋WEIPeng危威WEIWei

价值工程 2014年28期

张清鸾ZHANG Qing-luan；魏朋WEI Peng；危威WEI Wei

（昆明理工大学国土资源工程学院，昆明 650093）

（Faculty of Land Resource Engineering，Kunming University of Science and Technology，Kunming 650093，China）

0 引言

在GPS 精密单点定位技术中，需要提供卫星的精密轨道和钟差。目前，国际GNSS 服务组织（International GNSS Service，IGS）已能提供预报时长仅需3 小时的、精度5cm 的卫星轨道预报，但是在钟差预报方面，IGS 所提供的SP3 精密星历中的钟差数据虽能达到0.1ns 的精度以满足厘米级的定位要求，但有13 天的延时性，无法满足实时定位要求，所以卫星钟差的预报对精密单点定位有着及其重要的意义。目前，对于卫星钟差短期常用二次多项式模型实施预报，它是一类以时间为变量的函数模型，其基本算法是通过最小二乘原则对模型参数进行估计，代入模型对卫星钟差进行预报，文章通过另一种算法即总体最小二乘原则对模型参数进行估计，并比较两类算法的预报精度。

1 数学模型

1.1 基本模型

目前常用的卫星钟差短期短期预报模型为二次多项式模型，该模型的实质是将幂函数作为幂函数对时间间隔均匀的钟差时间序列做拟合，基本模型如下：

卫星钟在时刻t 的钟差一般可表示为

其中a0、a1、a2为待估参数，a0表示t0时刻原子钟的钟差，a1表示t0时刻该原子钟的钟速（频偏），a2表示t0时刻该原子钟的半加速度（频漂项）。其中，若时钟读数秒长均匀，a2应为零。

1.2 模型参数的最小二乘估计

设相对于时刻t1，t2，…，tn的卫星钟差为x1，x2，…，xn，其观测误差为vi，可由式（1）建立误差方程

则（3）可写为

按最小二乘估计原则，有估计值

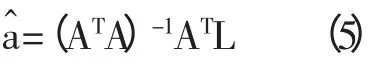
1.3 模型参数的总体最小二乘估计

当观测方程系数阵以及观测值均含有随机误差时，最小二乘解为有偏，此时顾及系数阵随机误差，按总体最小二乘准则估计计算出的总体最小二乘解则是无偏的。该结论已被文献[3]所证明，此时，令观测值随机误差向量

式（4）系数阵随机误差向量为σA，则有如下误差方程：

由该估计原则有

式（7）中的参数估值可由迭代法解得，具体方法如下：

2 算例分析

选取2013 年12 月29 日的事后SP3 精密星历PG01与PG02 两个卫星的钟差数据，依据二次多项式模型按最小二乘估计原则进行计算分析，发现其中t0（2013 年12 月29 日0 时0 分0 秒）时刻两颗卫星原子钟的半加速度a2（频漂项）的估计值分别为-1.3×10-7和0.9×10-7，不为零，说明时钟读数的秒长并不均匀，误差方程的系数阵A 含有误差。所以，对卫星钟差预报的二次多项式模型参数应按照总体最小二乘原则进行估计。

对PG01、PG02 两颗卫星2013 年12 月31 日的钟差依据二次多项式模型分别按最小二乘估计原则和总体最小二乘估计原则，进行短期预报，以该日的事后SP3 精密星历钟差数据作为真值，比较预报精度。

结果如图1、图2。

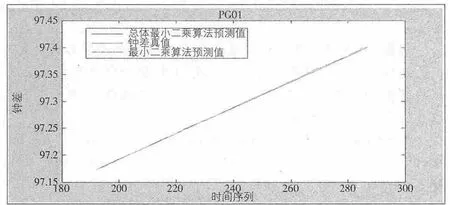
图1

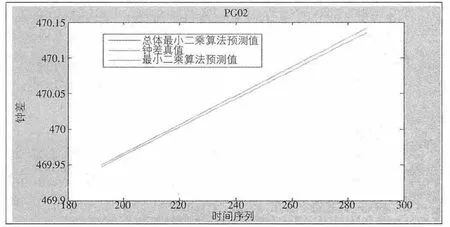
图2

以上结果表明，从第三天短期预测结果上，总体最小二乘算法与最小二乘算法预报结果接近。从预报中误差来看，令σ、σ′分别为总体最小二乘算法与最小二乘算法预报中误差，有σPG01=±1182.4ps，σ′PG01=±1182.8ps；σPG02=±4510.9ps，σ′PG02=±4511.0ps；σPG01＜σ′PG01，σPG02＜σ′PG02。