水泥基材料绝热温升曲线特征及速率表达式

王国杰，郑建岚

（1.福建江夏学院 工程学院，福建 福州 350108；2.福建省环保节能型高性能混凝土协同创新中心，福建 福州 350108）

混凝土绝热温升是结构温度场有限元仿真分析的关键参数.由于绝热温升值和温升速率能反映水泥基材料中胶凝材料水化速率和水化程度，故其也是反映水泥基材料水化性能的重要参数.

进行绝热温升试验，得到不同类型或配合比的水泥基材料绝热温升与龄期之间的关系，并通过数学表达式对试验结果进行拟合，是发展绝热温升预测模型的基础.目前已有一些混凝土绝热温升的经验表达式.水泥基材料绝热温升是绝热条件下胶凝材料水化的一种外在表现，因此绝热温升表达式与胶凝材料水化模型具有相同的函数形式，可以互用.目前常用的水泥基材料绝热温升和水化模型有：（1）单参数指数式［1］；（2）复合指数式［1］；（3）双曲线函数式［2－3］；（4）考虑温度影响的指数式［4］；（5）考虑浓度、温度影响的复合指数表达式［5］；（6）Byfors［6］，McCullough－Rasmussen 模 型［7］；（7）Freiesleben－Pedersen模型［8］；（8）de Schutter－Taerwe模型［9］.

以上模型中，除模型（8）以水化度为自变量外，其余均以时间（或水泥基材料的龄期）为自变量.各模型都能较好地表示较长龄期的绝热温升（水化度），对温升（水化）速率的拟合能力各不相同，但都存在一定的局限.例如模型（1），（2）的表达式，其对时间的导数曲线单调下降，与实际温升速率曲线形状不符，无法描述峰值点以前的温升速率.尽管可以描述速率曲线下降段，但与试验结果在时程上有较大差距.模型（3）的表达式，其对时间的导数曲线也是单调下降的，不能描述峰值点前的温升速率，但能很好地模拟衰减期的绝热温升发展规律，且能较好地预测最终温升，其中的参数也有一定物理意义.模型（4）～（7）的温升速率函数在形状上有类似绝热温升速率曲线的4个阶段，但各参数物理意义不明确，不独立，且相互影响，难以兼顾各阶段的模拟效果.模型（8）可以较好地描述温升速率曲线的各个阶段，但其以水化度而不是以时间为变量，需事先由试验得到水化度与时间的关系.

综上所述，尽管已有模型都能较好地对绝热温升（水化）速率的衰减期阶段进行拟合，但对诱导期、温升速率加速期、减速期的拟合效果往往不够理想，或者难以兼顾各个阶段的模拟效果，导致将其用于早龄期温度场的模拟时，与实际结果有较大差距.

本文基于对不同类型水泥基材料所进行的绝热温升试验，通过分析水泥基材料绝热温升速率的发展规律，提出新的针对水泥基材料绝热温升速率的表达式.

1 试验研究

1.1 原材料和配合比

为了研究不同类型水泥基材料的绝热温升规律并得到具有代表性的温升速率表达式，本文选用了普通泵送混凝土NC－1、单掺粉煤灰的自密实混凝土SCC－1、粉煤灰和矿渣复掺的自密实混凝土SCC－2、高强混凝土灌浆料UGM－1共4种水泥基材料进行试验研究.所用的原材料为：P·O 42.5水泥（C），比表面积360 m2／kg；Ⅰ级粉煤灰（FA），比表面积391m2／kg；S95粒化高炉矿渣微粉（GGBS），比表面积414m2／kg；细度模数为2.8的河砂（S），表观密度2 640kg／m3；花岗岩碎石（G），粒径为5～10mm，堆积密度1 575kg／m3，表观密度2 689kg／m3；硅灰（SF），粒径范围0.113～2.908μm，平均粒径0.963μm；萘系粉状高效减水剂（SP），减水率20%（质量分数）.4种水泥基材料配合比见表1.

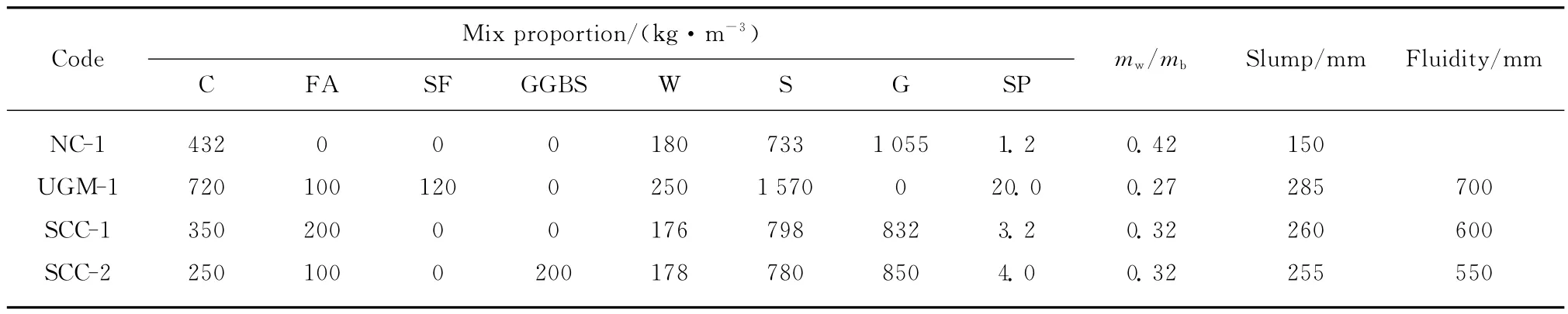
表1 水泥基材料配合比Table 1 Mix proportion of cement－based materials

1.2 绝热温升试验方案

通过HR－2型混凝土热物理参数测定仪测试水泥基材料绝热温升.试样体积50L，从试样制备好入模起通过计算机以30min间隔自动采集试样中心温度.试样入模温度TI见表2.

2 试验结果分析

2.1 绝热温升曲线、温升速率曲线的特点

试验得到水泥基材料绝热温升θ（τ）随龄期τ的变化曲线见图1（其中试样UGM－1在24h后的绝热温升即已超过仪器上限温度）；通过以短而均匀的时间间隔采集试样温度变化数据，求得其绝热温升速率dθ（τ）／dτ随龄期τ 的变化曲线［1］见图2；将试验结果表示为以龄期τ 为横坐标，τ／θ（τ）为纵坐标的曲线，即“时间／温升”曲线，如图3所示.

由图1～3可以看出，尽管不同试样的胶结料用量、水胶比、掺和料种类等配合比因素各不相同，但4种水泥基材料的绝热温升曲线、绝热温升速率曲线、时间／温升曲线却有着相似的形状和特点.即都经历了诱导期（阶段Ⅰ）、温升速率加速期（阶段Ⅱ）、温升速率减速期（阶段Ⅲ）、衰减期（阶段Ⅳ）4个阶段.与水泥水化过程分为5个阶段［6］有所不同，由于搅拌、入模和测试准备时间一般大于0.5h，故混凝土绝热温升试验往往无法捕捉到水泥水化诱导前期阶段，该阶段对混凝土绝热温升的影响体现为入模后其温度比环境温度高1～3℃.

图1 绝热温升曲线Fig.1 Adiabatic temperature rise vs age

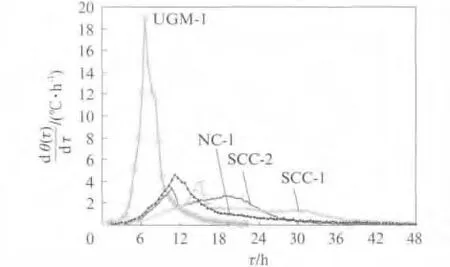
图2 绝热温升速率曲线Fig.2 Adiabatic temperature rise rate vs age

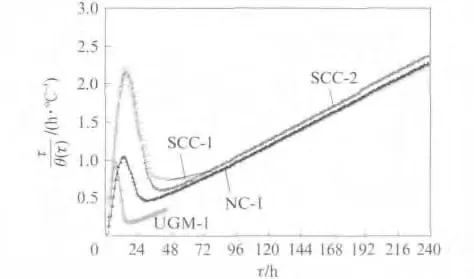
图3 时间／温升曲线Fig.3 Time divided by the temperature rise vs age

2.2 绝热温升各阶段分界点的确定方法

为了更深入地分析水泥基材料绝热温升在不同阶段的特点，有必要对不同阶段分界点进行确切定义，从而对水泥基材料绝热温升的4个阶段进行明确划分.

以试样SCC－2为例，图4给出了其绝热温升速率dθ（τ）／dτ曲线与时间／温升τ／θ（τ）曲线的对应关系.可以发现：τ／θ（τ）曲线在诱导期处于上升阶段，到诱导期末曲线达到向上的峰值；在加速期该曲线显著下降，并在与dθ（τ）／dτ曲线峰值点对应的时刻出现转折；在温升速率减速期CD 段，τ／θ（τ）曲线下降（dθ（τ）／dτ曲线中有第2个温升峰时）或略有上升（dθ（τ）／dτ曲线中只有1个温升峰时）；减速期与衰减期的分界点在τ／θ（τ）曲线和dθ（τ）／dτ 曲线上都不明显，但在τ／θ（τ）曲线上有1个转折点（D 点），该点以后整个衰减期近似1条上升的射线.由图3可见，4种水泥基材料的τ／θ（τ）曲线形状一致，都具有上述分段特征.

图4 温升速率曲线和时间／温升曲线的对应关系Fig.4 Corresponding relation between dθ（τ）／dτandτ／θ（τ）curve

以τ／θ（τ）曲线向上的峰值点发生的时刻作为诱导期末时间，标志着温度开始迅速增长，其增幅从此开始大于时间的增幅，绝热温升进入温升速率加速期.

以τ／θ（τ）曲线经过峰值点后，下降到最低值开始反降为升的时刻作为减速期末点（即衰减期起点D 点）.可以通过对τ／θ（τ）曲线求导的方法得到D点的横坐标，如图5所示.

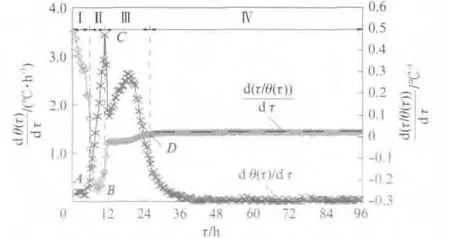
图5 衰减期起点的确定Fig.5 Determination of the starting moment of decay stageⅣ

2.3 最终温升的预测方法

水泥基材料在龄期为无穷大时的最终温升θ∞是大体积混凝土温度场模拟中的重要参数，但由于试验不可能无限期持续，因此无法通过试验直接获得.实践中往往参照文献［1］的做法，将绝热温升曲线近似为1 条双曲线，直接用直线来模拟整条τ／θ（τ）曲线，然后求直线斜率的倒数，即可由试验结果预测最终温升θ∞.但由试验结果可见（见图3，4），在τ／θ（τ）曲线上只有D 点以后的部分才近似为直线.说明只有在衰减期，绝热温升曲线才近似于双曲线，而在诱导期、温升速率加速期和减速期，绝热温升曲线与双曲线都相差甚远.尤其是掺加粉煤灰、矿渣等掺和料的试样，例如SCC－2，其在前面几个阶段所经历的时间往往更长，衰减期推迟，导致用文献［1］的做法求其最终温升时，预测值存在较大误差.

按上节提出的分界点确定方法对τ／θ（τ）曲线分段以后，舍去图3 各曲线中温升速率减速期末点（D 点）以前的曲线，结果如图6所示.以D 点以后直线部分的斜率的倒数求最终温升θ∞，将所得结果与用传统方法（按文献［1］）预测得到的结果对比（见表2最后2列）后发现，两者相差较大.表明最终温升θ∞是由进入扩散阶段（衰减期）后温升曲线的变化趋势决定的，与此前所经历的阶段并无必然联系.本文所提出的先对τ／θ（τ）曲线分段，然后以D 点以后直线部分的斜率的倒数求最终温升θ∞的方法，能较好地反映进入衰减期后绝热温升曲线按照双曲线规律变化的趋势，得到的最终温升预测值更为准确、合理.

图6 用衰减期数据预测最终温升Fig.6 Prediction of final temperature rise through slope of theτ／θ（τ）curve

2.4 不同水泥基材料的水化规律分析

根据本文对绝热温升各阶段分界点的定义，对4种水泥基材料的试验结果进行处理，得到各试样在诱导期末点时间t0，温升速率峰值点时间tp，衰减期起点时间（即减速期末点时间）td时刻的温升速率值dθ／dτ，温升值θ，水化度DH（该值通过该时刻的温升值与最终温升的比值得到），以及温峰宽度td－t0（即温升速率加速期与减速期合起来的持续时间），最终温升预测值θ∞，见表2 所示，其中TI为入模温度.

表2 水泥基材料绝热温升曲线各阶段的特征值Table 2 Characteristic values of each stage in adiabatic temperature rise curve of four samples

由表2可以看出，各水泥基材料进入诱导期、温升速率加速期和减速期、衰减期的时间不同：掺加硅灰且水泥用量高的高强混凝土灌浆料UGM－1水化进程最快，在入模后6.58h 即达到温升速率峰值点，9.10h后进入衰减期；单掺粉煤灰的自密实混凝土SCC－1水化进程最慢，到15h后才达到峰值点，23h后进入衰减期；诱导期的温升速率随入模温度、配合比的不同而不同，但诱导期末的水化度则较为接近，作者通过大量试验发现，诱导期末的平均水化度约为5%（本文4种水泥基材料的平均值为7%）；到达温升速率峰值点的时间和峰值点温升速率差别都较大，达到温升速率峰值点时的水化度为23%～34%；达到减速期末点的时间、减速期末点温升速率相差很大.各特征值主要受入模温度、胶凝材料性能和配合比影响.

3 绝热温升速率表达式

基于上述绝热温升过程分段方法，根据不同阶段绝热温升速率曲线的特点，本文用一个新的函数模型来构建绝热温升速率表达式.

3.1 表达式的建立

根据以上试验结果，温升速率曲线的特点为：有1个明显的主峰，在达到峰值点之前曲线单调上升，之后下降；有明显的4个阶段，诱导期温升在总温升中占比约5%，诱导期结束时间代表了混凝土剧烈升温的开始；温升速率峰值点是曲线中最关键的点，该点的横坐标是达到温升速率峰值点的时间，纵坐标是峰值点温升速率值.此外，温升速率加速期与减速期的曲线并不对称，加速期曲线短而变化迅速，减速期曲线较长且变化缓慢（当掺加粉煤灰、矿渣时，表现得更为明显）.衰减期很长但是温升速率低，该阶段可以用双曲线较好地模拟.当掺加粉煤灰、矿渣等掺和料时，温升速率曲线减速期出现平峰或第2个峰值点.

根据温升速率曲线的特点，本文以名义温升速率峰值点作为关键点，构建一个新的函数模型——4参数表达式：

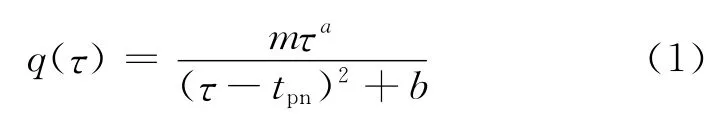
式中：q（τ）为τ时刻的温升速率；tpn，b，a，m 为常数.

式（1）中tpn的意义与表2中tp类似，为到达温升速率名义峰值点的时间，其作用是确定温峰中点的横坐标；b的作用是调整温峰宽度，即代表了加速期与减速期持续时间之和的大小；a 用于调节温升曲线后期的升降（温升速率曲线衰减期的发展趋势），当0＜a＜1时，q（τ）曲线能很好地模拟温升速率曲线，同时曲线形状与绝热温升曲线相似，且曲线存在相当于最终温升θ∞的极限值.确定了以上参数后，最终通过m 值来调节温升速率峰值点高度.实际上m 值与tpn，b，a 这3 个参数有关.tpn越小，m 值越大；a，b值越小，m 值也相应减小.因此m 尽管有一定的物理意义，但并不完全独立.

由此得到本文温升速率表达式中4个参数的物理意义，分别为：tpn是温升速率名义峰值点时间（通常对应于峰值点时间，当掺加掺和料导致温升速率峰明显不对称时，为温升速率峰中点对应的时间）；b是温峰宽度，即温升速率加速期与减速期的持续时间之和；a是衰减期温升程度指标；m 是温升速率峰值大小（最终温升）调节系数.

3.2 表达式计算结果与试验结果对比

图7给出了4种水泥基材料绝热温升速率试验曲线用本文函数模型拟合的结果，图8给出了对本文函数模型拟合的绝热温升速率进行积分所得到的绝热温升曲线的拟合效果.

图7 本文函数模型对绝热温升速率试验曲线的拟合效果Fig.7 Comparison between model results and test results of adiabatic temperature rise rate

由图7，8可以看出，对于本文4种水泥基材料，用本文函数模型所计算的结果与试验结果都很接近，无论是绝热温升曲线还是绝热温升速率曲线，拟合效果都较理想.与已有模型表达式的拟合效果相比，本文函数模型对衰减期以前的绝热温升曲线和绝热温升速率曲线的拟合能力有明显优势.虽然本文提出的绝热温升速率模型曲线只有1个峰，但对于掺加粉煤灰、矿渣试样的实际温升速率曲线有双峰或平台段的情况，也能通过调整温峰中心与温峰宽度而取得较好的拟合效果.

图8 本文函数模型对绝热温升试验曲线的拟合效果Fig.8 Comparison between model results and test results of adiabatic temperature rise

较好的拟合效果归因于本文函数模型中参数的选取：以绝热温升速率峰值点时间、大小以及温峰宽度作为主要参数，能抓住绝热温升速率曲线的主要特点.具有独立意义的参数在确定和调整上具有较大的灵活性.通过专门的参数a 来考虑衰减期的影响，可以对长龄期效果进行独立描述，克服了早龄期和长龄期难以兼顾的问题.

作为对比，图9给出了常用的单参数指数模型（single parameter exponential function，SE）、双参数指数模型（double parameters exponential function，DE）、双曲线模型（hyperbolic function）、Freiesleben等［8］提出的3 参数指数模型（FHP）的表达式对试样SCC－1的绝热温升和绝热温升速率曲线的拟合效果.

图9 已有模型对绝热温升试验曲线和温升速率试验曲线的拟合效果Fig.9 Comparison of results calculated by different existing models

由图9可见，已有的模型能较好地拟合绝热温升曲线的总体趋势，但由于表达式的局限，导致它们并不能很好地拟合绝热温升速率曲线的形状和进程.与图7，8相比，显然本文提出的4参数表达式在水泥基材料早龄期的绝热温升与温升速率方面具有更好的拟合效果.

4 结论

（1）通过以短时间间隔自动采集到的绝热温升试验数据，可以得到较为完整的水泥基材料绝热温升速率曲线和时间／温升曲线.基于这些曲线可以得到确切的诱导期末点时间和减速期末点时间，从而对水泥基材料绝热温升速率4 个阶段进行明确划分.

（2）不同配合比的水泥基材料绝热温升速率曲线都有4个明显的阶段，但水化进程却有较大差别.水泥基材料水化进程主要受入模温度、胶凝材料种类和配合比的影响.不同入模温度和配合比下，诱导期的绝热温升速率有所不同，但水化度较为接近，平均为5%.

（3）进入衰减期前，绝热温升曲线与双曲线有较大差别；进入衰减期后与双曲线非常近似.在对最终温升进行预测时，有必要舍去τ／θ（τ）曲线衰减期前的数据，仅用衰减期的数据对最终温升进行预测.对于具有大掺量掺和料（或水化进程慢）的水泥基材料，用这种修正方法预测的最终温升精度将大幅提高.

（4）提出通用的水泥基材料4参数表达式，它对绝热温升曲线和绝热温升速率曲线都有较好的拟合效果.该表达式的参数具有相对明确的物理意义并便于调整.

（5）研究结果为建立绝热温升速率表达式参数与水泥基材料配合比参数之间的关系奠定了基础，并有望进一步通过等效龄期来考虑温度对水化过程的影响，发展新的水泥基材料绝热温升（水化）预测模型.

［1］朱伯芳.大体积混凝土温度应力与温度控制［M］.北京：中国电力出版社，1999：19－20.ZHU Bofang.Thermal stresses and temperature control of mass concrete［M］.Beijing：China Electric Power Press，1999：19－20.（in Chinese）

［2］张子明，冯树荣，石青春，等.基于等效时间的混凝土绝热温升［J］.河海大学学报：自然科学版，2004，32（5）：573－577.ZHANG Ziming，FENG Shurong，SHI Qingchun，et al.Adiabatic temperature rise of concrete based on equivalent time［J］.Journal of Hohai University：Natural Science，2004，32（5）：573－577.（in Chinese）

［3］张子明，宋智通，黄海燕.混凝土绝热温升和热传导方程的新理论［J］.河海大学学报：自然科学版，2002，30（3）：1－6.ZHANG Ziming，SONG Zhitong，HUANG Haiyan.New theory on adiabatic temperature rise and heat conduction equation of concrete［J］.Journal of Hohai University：Natural Science，2002，30（3）：1－6.（in Chinese）

［4］朱伯芳.混凝土绝热温升的新计算模型与反分析［J］.水利发电，2003，29（4）：29－32.ZHU Bofang.A new computing model for the adiabatic temperature rise of concrete and the method of back analysis［J］.Water Power，2003，29（4）：29－32.（in Chinese）

［5］凌道盛，许德胜，沈益源.混凝土中水泥水化反应放热模型及其应用［J］.浙江大学学报，2005，39（11）：1695－1698.LING Daosheng，XU Desheng，SHEN Yiyuan.Model for hydration heat of cement in concrete and its application［J］.Journal of Zhejiang University，2005，39（11）：1695－1698.（in Chinese）

［6］BYFORS J.Plain concrete at early ages［D］.Stockholm：Swedish Cement and Concrete Research Institute，1980.

［7］McCULLOUGH B F，RASMUSSEN R O.Fast track paving：Concrete temperature control and traffic opening criteria for bonded concrete overlays［R］.［S.l.］：Department of Transportation，1999.

［8］FREIESLEBEN H P，PEDERSEN E J.Curing of concrete structures，draft DEB－guide to durable concrete structures：Appendix 1 ［R］.Lausanne：Comite Euro－International du Beton，1985.

［9］de SCHUTTER G，TAERWE L.General hydration model for Portland cement and blast furnace slag cement［J］.Cement and Concrete Research，1995，25（3）：593－604.