全球大洋潮汐模式在南海的准确度评估*
2014-11-28高秀敏魏泽勋吕咸青王永刚
高秀敏,魏泽勋*,吕咸青,王永刚,杨 扬
(1.国家海洋局 第一海洋研究所 海洋环境与数值模拟研究室,山东 青岛266061;2.中国海洋大学 物理海洋实验室,山东 青岛266100;3.国家海洋信息中心,天津300171)
潮汐潮流数值模拟中,开边界的选取至关重要。通常情况下,都是将大区域结果插值到区域模式边界上,或利用观测资料进行估计,作为区域模式的开边界条件。目前,国际上有几十种全球大洋潮汐模式,很多区域潮波模式的边界条件都是来自于这些全球模式,因此,对这些全球模式在研究区域进行准确度评估至关重要。
全球大洋潮汐模式的建立开始于20世纪80年代。Schwiderski[1-3]建立了水动力模式,并将验潮站资料同化到模式中,给出了比较精确的全球大洋潮汐模式。Cartwright等[4]根据Geosat卫星高度计资料给出了第一个基于卫星高度计的全球大洋潮汐模型。随着1992年TOPEX/Poseidon(以下简称T/P)卫星的发射,基于T/P及其后续Jason卫星高度计资料的大洋潮汐模式得到了快速发展,且精度有了很大的提高。目前常见的大洋潮汐模式有美国空间飞行研究中心的CSR(Center for Space Research)模式①EANES R J,BETTADPUR S V.The CSR3.0global ocean tide model:Diurnal and semi-diurnal ocean tides from TOPEX/POSEIDON altimetry.Technical Report CRS-TM-96-05,Centre for Space Research,University of Texas,Austin,Texas,1996.,NASA戈达德太空飞行中心的 GOT(Goddard Ocean Tide)模式②RAY R D.A global ocean tide model from TOPEX/POSEIDON altimetry:GOT99.2.NASA/TM-1999-209478,Goddard Space Flight Centre,Greenbelt,MD,USA,1999.,法国潮汐工作组的 FES(Finite Element Solution)模式[5-8],美国俄勒冈大学的 TPXO 模式[9-10]和日本国立天文观测台的 NAO 模式[11]等。这些模式大都基于水动力学方程组,并将卫星高度计资料和验潮站资料同化到模式中。
Andersen等[12]对12种全球大洋潮汐模式进行了比较评估,指出对于 M2和K1分潮,Schrama等[13]与验潮站数据符合最好,对于S2和O1分潮,Egbert等[9]与验潮站数据符合最好。Shum等[14]指出1994年以来新发展了20多种全球大洋潮汐模式,并对其中的10种模式进行了准确度评估,对于M2分潮,SR95.0/.1[13]与验潮站数据符合最好。Penna等[15]对常用的大洋潮汐模式(NAO.99b,FES94.1,GOT00.2,TPXO.6.2,CSR3.0)进行了简单的介绍。汪一航等[16]依据中国近海18个岛屿的调和常数对5个大洋潮汐模式(NAO99,GOT00,FES2002,FES2004,TPXO7)的准确度进行了检验,结果表明,日本国家天文台的潮汐模式NAO99在中国近海的结果相对较准确。Gladkikh等[17]利用新西兰沿岸7个验潮站分析了全球大洋模式 TPXO7.2、GOT00.2、NAO.99b、FES2004和EOT10a[18]的准确度,对比结果表明在新西兰沿岸 TPXO 7.2与验潮站数据符合最好。李大炜等[19]利用传统验潮站数据对 NAO99b、FES2004、GOT4.7、TPXO7.2和EOT10a五个全球大洋潮汐模式进行精度评估,结果表明,在中国近海,NAO99b的精度最高,EOT10a在全球海洋范围综合指标最优。
本研究选取了全球大洋潮汐模式TPXO7.2、GOT00.2、NAO.99b和DTU10[20],分析了它们在南海区域M2、S2、K1、O1分潮的分布特征,并利用验潮站资料和T/P卫星高度计资料对它们的准确度进行了评估。
1 模式介绍
TPXO模式是由美国俄勒冈大学(Oregon State University)建立的反演同化模式,该模式以拉普拉斯潮汐方程组为基础,并同化了T/P、Jason卫星高度计资料和验潮站资料。TPXO7.2为其最新版本,分辨率为0.25°×0.25°,网格数为1440×721,纬度-90°~90°N,经度0.25°~360°E,此模式提供了8个主要分潮 M2,S2,N2,K2,K1,O1,P1和 Q1,2个长周期分潮 Mf,Mm和3个浅水分潮 M4,MS4,MN4共13个分潮的潮汐信息。TPXO7.2模式的下载网址为http://volkov.oce.orst.edu/tides/global.html。
GOT模式是由 NASA戈达德太空飞行中心(Goddard Space Flight Center)研发的,GOT00.2是 GOT99.2b的升级版本,分辨率为0.5°×0.5°,网格数为720×361,纬度-90°~90°N,经度0°~359°30′E。该模式是基于FES94.1动力学模型的,并对FES94.1模型进行修正,它还融合了T/P和ERS 1/2卫星数据。GOT00.2模式的下载网址为http://www.mmnt.net/db/0/0/falcon.grdl.noaa.gov/pub/dave/GOT00.2。
NAO.99b模式是日本国立天文观测台(National Astronomical Observatory)开发的,分辨率为0.5°×0.5°,网格数为720×360,纬度-89°45′~89°45′N,经度0.25°~359°45′E。该模型将大约5a的T/P卫星测高数据同化到动力学模型,给出了16个短周期分潮(M2,S2,K1,O1,N2,P1,K2,Q1,M1,J1,OO1,2N2,Mu2,Nu2,L2和T2)和7个长周期分潮(Mtm,Mf,MSf,Mm,MSm,Ssa和Sa)的结果。NAO.99Jb为区域模式,范围为纬度20°~65°N,经度110°~155°E,分辨率为1/12°×1/12°,另外还同化了沿岸验潮站数据。NAO.99b模式的下载网址为http://www.miz.nao.ac.jp/staffs/nao99/index_En.html。
DTU10模式是近期出现的全球大洋潮汐模式,是丹麦科技大学(Technical University of Denmark)开发的,分辨率为0.125°×0.125°,网格数为2881×1441,纬度-90°~90°N,经度0°~360°E。该模式是基于FES2004[8]和响应法[21],并利用从1992-09-2009-09的17a的 T/P、Jason-1和Jason-2卫星高度计资料发展起来的一个新的全球大洋潮汐模型,包含8个主要分潮 M2,S2,N2,K2,K1,O1,P1,Q1,此外,还包含2个来自于GOT4.7模式的 S1,M4分潮。DTU10模式的下载网址为http://www.space.dtu.dk/English/Research/Scientific_data_and_models/Global_Ocean_Tide_Model.aspx。
2 准确度评估方法
用振幅绝均差和迟角绝均差来表示计算值和观测值之间的偏差,这种方法比较直观。其计算公式为:
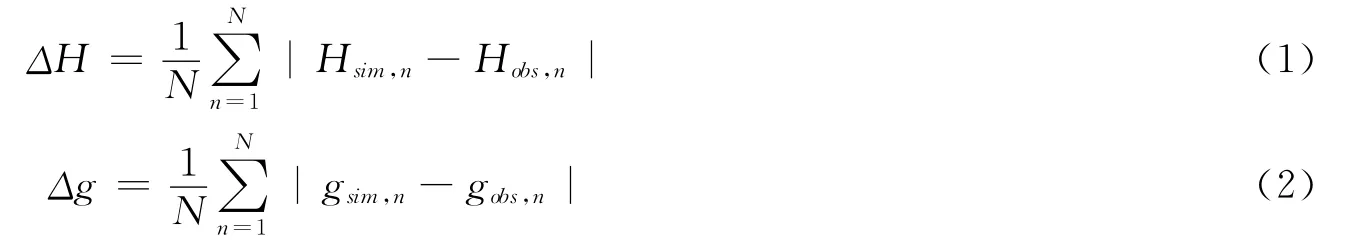
式中,H为振幅;g为迟角;下标sim和obs分别代表计算值和观测值;N为观测值个数,n=1,2,…,N。当振幅较小时,计算和观测的迟角都不太稳定,同时振幅较小时的误差对潮高计算误差影响也较小,故式(2)中不考虑振幅的差别而将所有迟角差进行平均并不十分合理。另一种方法不是很直观,但更合理一些,这种方法取均方根偏差:
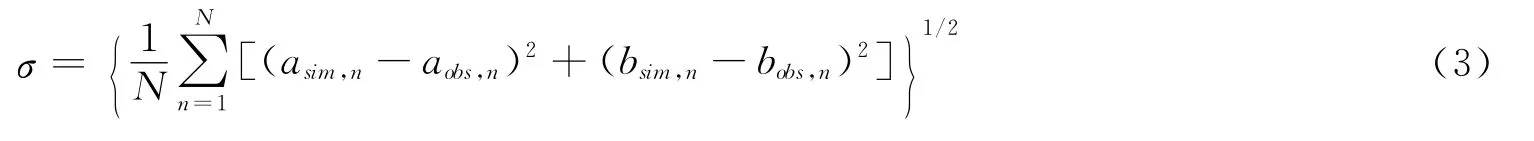
其中,

σ也常常被称为计算值和观测值之间的距离,它表征了计算值和观测值的偏离程度,而它与观测值变化性的相对偏离程度可用相对偏差

来表示,其中,
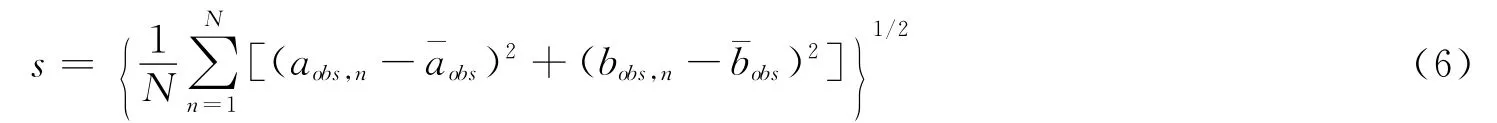

代表了计算值和观测值的拟合程度,r相当于线性回归中的相关系数。
3 大洋潮汐模式在南海的准确度评估
本研究采用60个验潮站和22个T/P卫星高度计轨道交叉点的调和常数资料(站位分布见图1,验潮站资料引自Fang等[22],其站名见表1)作为观测值,将全球大洋潮汐模式和观测资料全都插值到0.125°×0.125°的网格上,采用第2节描述的方法,对大洋潮汐模式TPXO7.2、GOT00.2、NAO.99b和DTU10中 M2,S2,K1和O1四个主要分潮调和常数在南海的准确度进行了评估。
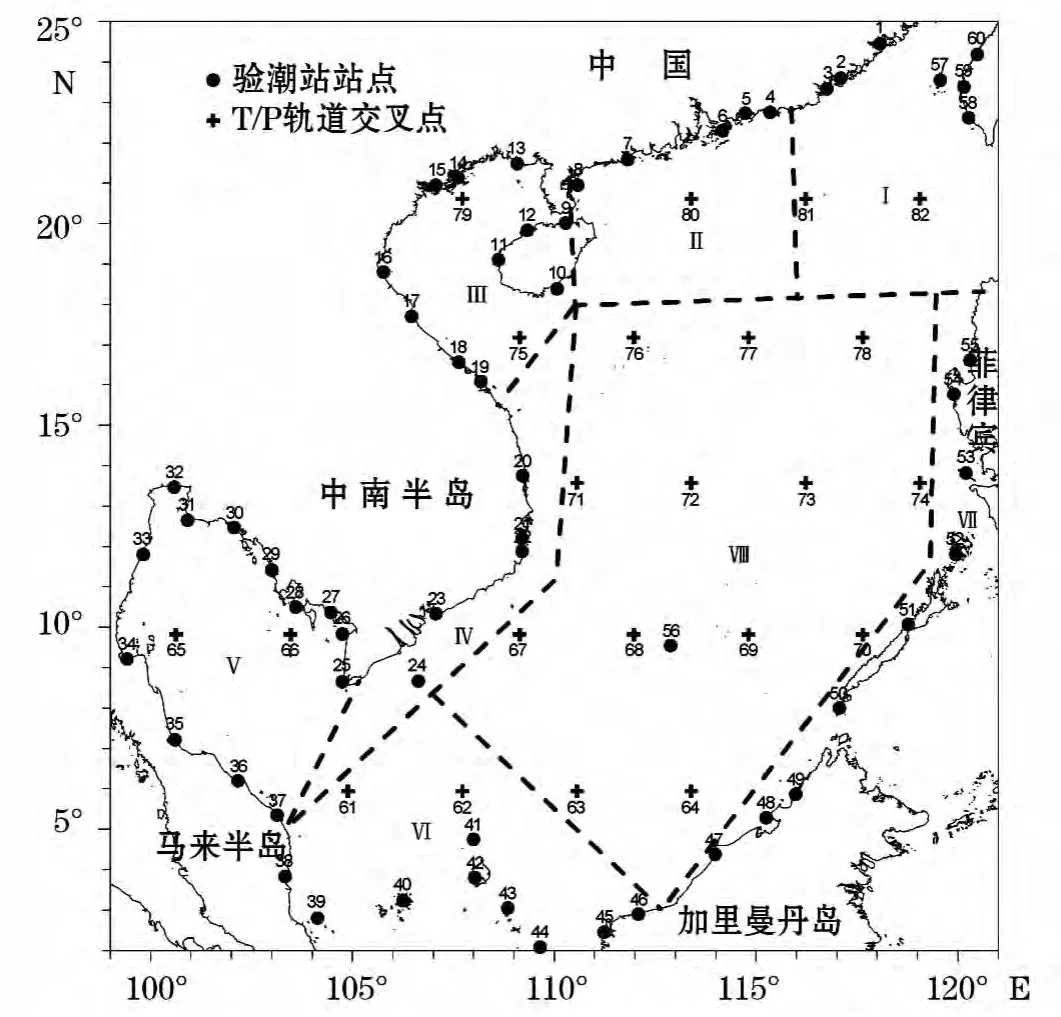
图1 验潮站站位和T/P轨道交叉点位置Fig.1 Locations of tidal gauge stations and T/P crossover points
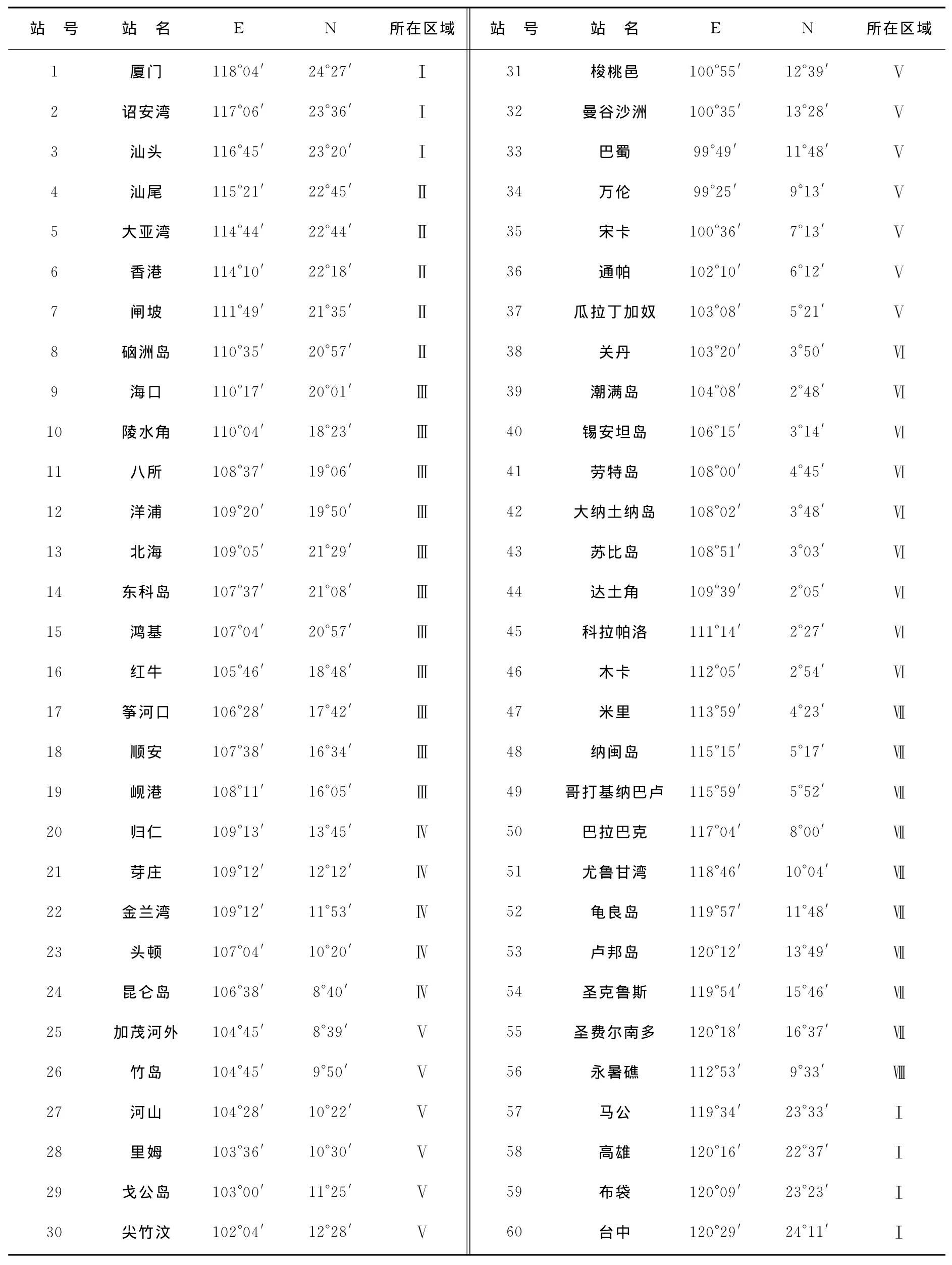
表1 验潮站对应站名Table 1 Names of tidal gauge stations
表2给出了4个大洋潮汐模式与验潮站调和常数的对比,从表中可以看出,对于M2分潮,TPXO7.2、GOT00.2、NAO.99b和DTU10的均方根偏差分别为13.63,11.00,15.37和8.36cm,DTU10结果最好,GOT00.2次之;对于S2分潮,TPXO7.2、GOT00.2、NAO.99b和DTU10的均方根偏差分别为6.28,10.14,8.38和5.22cm,DTU10结果最好,TPXO7.2次之;对于 K1分潮,TPXO7.2、GOT00.2、NAO.99b和DTU10的均方根偏差分别为11.01,6.63,7.42和7.18cm,GOT00.2结果最好,DTU10次之;对于 O1分潮,TPXO7.2、GOT00.2、NAO.99b和 DTU10的均方根偏差分别为10.23,7.32,7.56和7.57cm,GOT00.2结果最好,DTU10和NAO.99b偏差相差不大,TPXO7.2结果最差。
表3给出了4个大洋潮汐模式与T/P卫星轨道交叉点调和常数的对比,从表中可以看出,4个大洋潮汐模式的结果都很好,且相差不大。对于半日分潮,DTU10和NAO.99b的结果要好于GOT00.2和TPXO7.2;对于全日分潮,GOT00.2和DTU10的结果要好于NAO.99b和TPXO7.2。与表2相比,4个大洋潮汐模式与卫星高度计资料的误差明显小于与验潮站比较的误差。
表4给出了4个大洋潮汐模式与验潮站和T/P卫星轨道交叉点调和常数的对比,由于4个大洋潮汐模式在T/P卫星轨道交叉点处的偏差都很小且相差不大,因此表4的结果与表2只与验潮站调和常数对比的结果类似。
为了更精确地给出4个大洋潮汐模式在南海不同区域的准确度,文中将南海分成了8个区,见图1。区域Ⅰ位于台湾海峡和吕宋海峡附近,包括7个验潮站点(站号1~3,57~60)和2个T/P卫星轨道交叉点(站号81和82)。区域Ⅱ位于广东沿岸,包括5个验潮站点(站号4~8)和1个T/P卫星轨道交叉点(站号80)。区域Ⅲ位于北部湾,包括11个验潮站点(站号9~19)和2个T/P卫星轨道交叉点(站号75和79)。区域Ⅳ位于越南东南部,包括5个验潮站点(站号20~24)。区域Ⅴ位于泰国湾,包括13个验潮站点(站号25~37)和2个T/P卫星轨道交叉点(站号65和66)。区域Ⅵ位于巽他陆架上,包括9个验潮站点(站号38~46)和2个T/P卫星轨道交叉点(站号61和62)。区域Ⅶ位于加里曼丹岛和菲律宾群岛沿岸,包括9个验潮站点(站号47~55)。区域Ⅷ位于南海中央海盆,包括1个验潮站点(站号56)和13个T/P卫星轨道交叉点(站号63,64,67~74,76~78)。
表5为分区域的对比结果,这里只给出了均方根偏差。由表5可以看出,在区域Ⅰ,4个分潮均是DTU10的偏差最小;在区域Ⅱ,除了K1分潮GOT00.2的偏差最小外,另外3个分潮均是DTU10的偏差最小;在区域Ⅲ,4个分潮均是DTU10的偏差最小;在区域Ⅳ,M2分潮NAO.99b的偏差最小,S2和O1分潮GOT00.2的偏差最小,K1分潮DTU10的偏差最小;在区域Ⅴ,M2和S2分潮DTU10的偏差最小,K1和O1分潮NAO.99b的偏差最小;在区域Ⅵ,M2和O1分潮GOT00.2的偏差最小,S2和K1分潮DTU10的偏差最小;在区域Ⅶ,除了O1分潮GOT00.2的偏差最小外,另外3个分潮均是TPXO7.2的偏差最小;在区域Ⅷ,M2分潮NAO.99b的偏差最小,S2分潮TPXO7.2的偏差最小,K1和O1分潮GOT00.2的偏差最小。
对南海进行潮汐潮流数值模拟时,开边界主要位于台湾海峡北口的北边界、吕宋海峡处的东边界和卡里马塔海峡附近的南边界。北边界和东边界位于区域Ⅰ,在此区域,4个分潮都是DTU10结果最好。南边界位于区域Ⅵ,M2和O1分潮GOT00.2的偏差最小,S2和K1分潮DTU10的偏差最小。
图2~图5分别给出了4个大洋潮汐模式的南海M2、S2、K1、O1分潮的同潮图,其传播规律基本相同,在北部湾和泰国湾处略有差异。与Fang等[22]的结果相比,对于M2分潮,GOT00.2的结果最接近,对于S2分潮,DTU10的结果最接近;对于K1分潮,DTU10的结果最接近,对于O1分潮,NAO.99b的结果最接近。
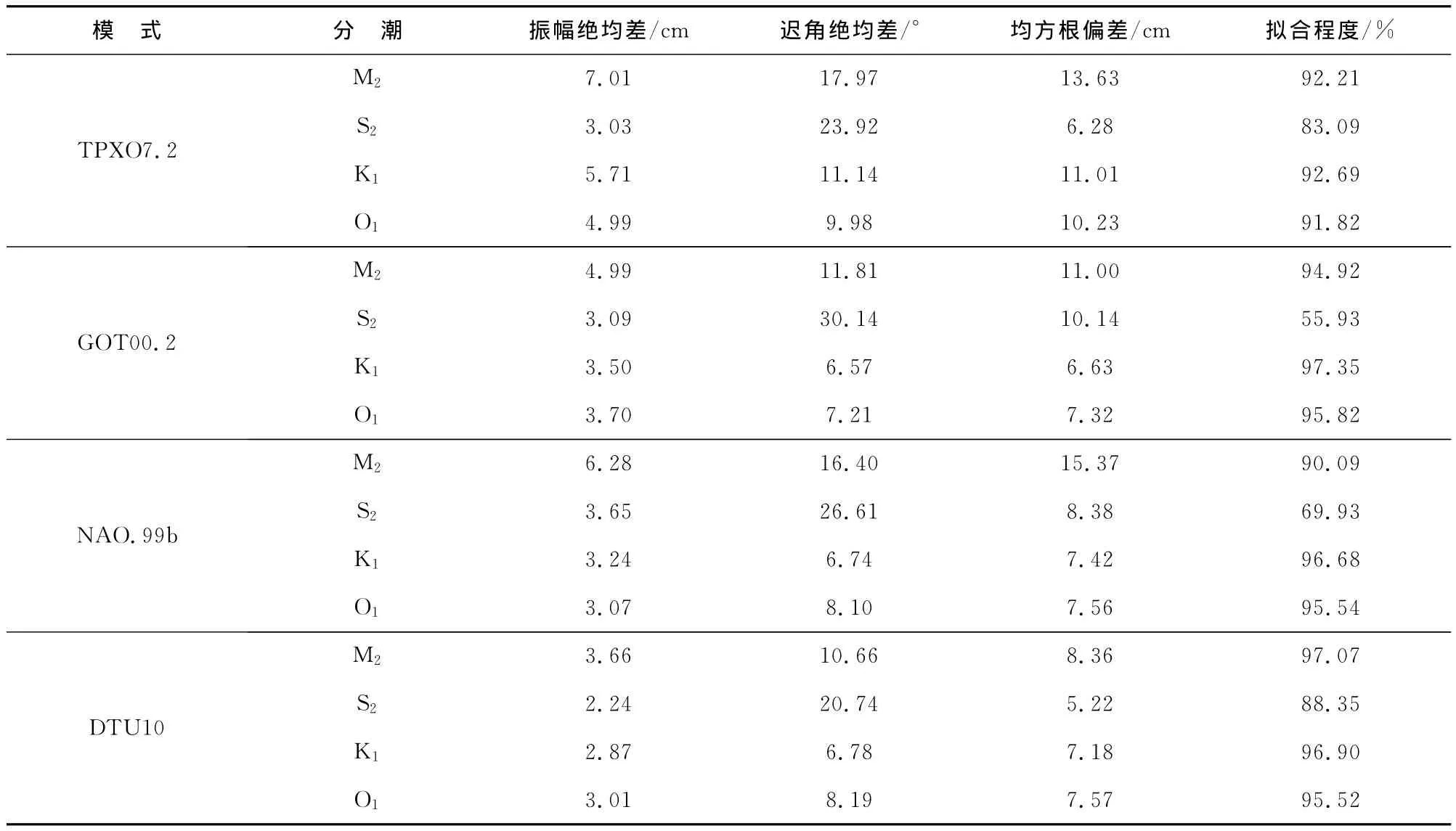
表2 与验潮站调和常数的对比Table 2 Comparison with the harmonic constants observed at the tidal gauge stations
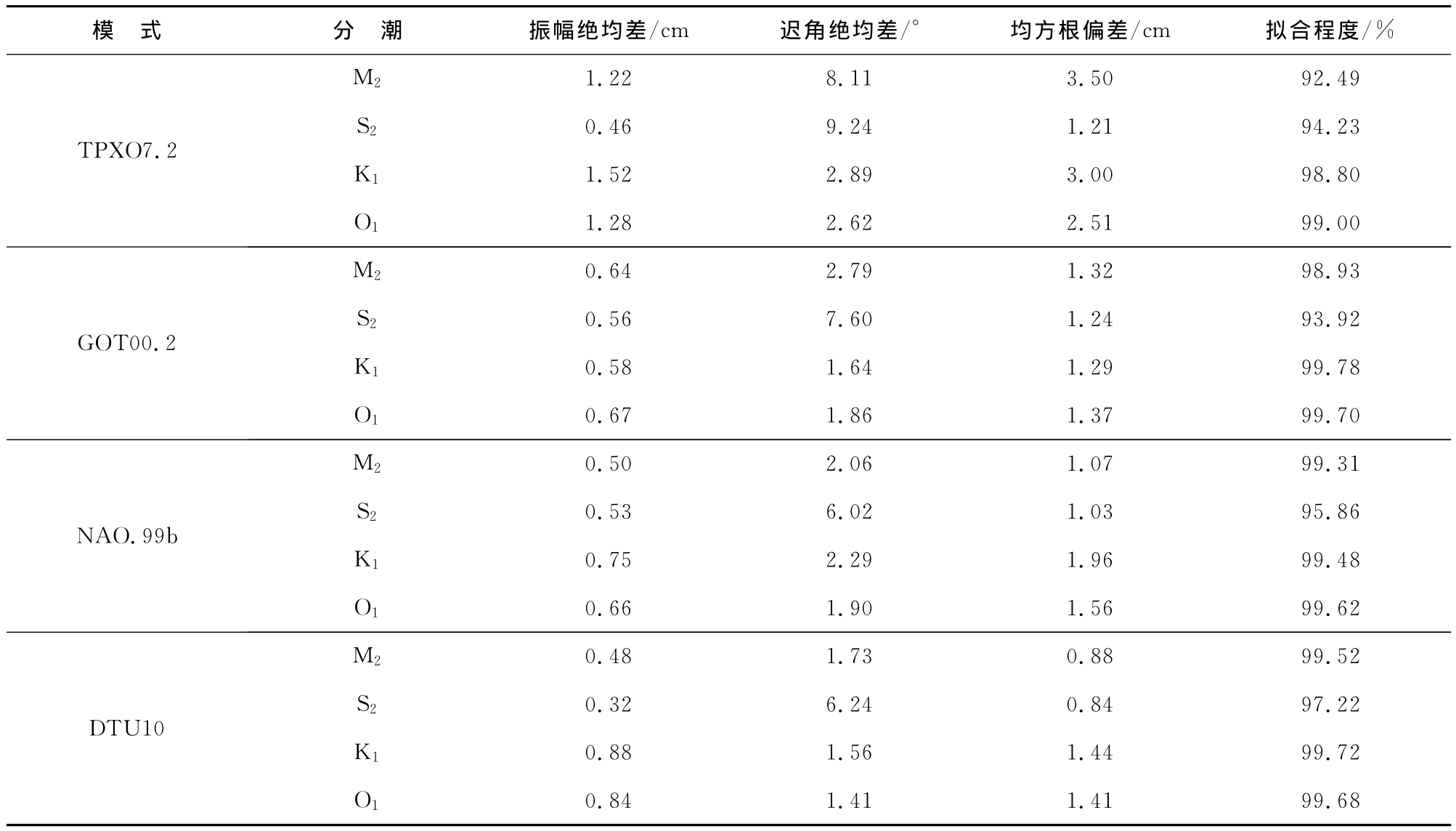
表3 与T/P卫星轨道交叉点调和常数的对比Table 3 Comparison with the harmonic constants observed at the T/P crossover points
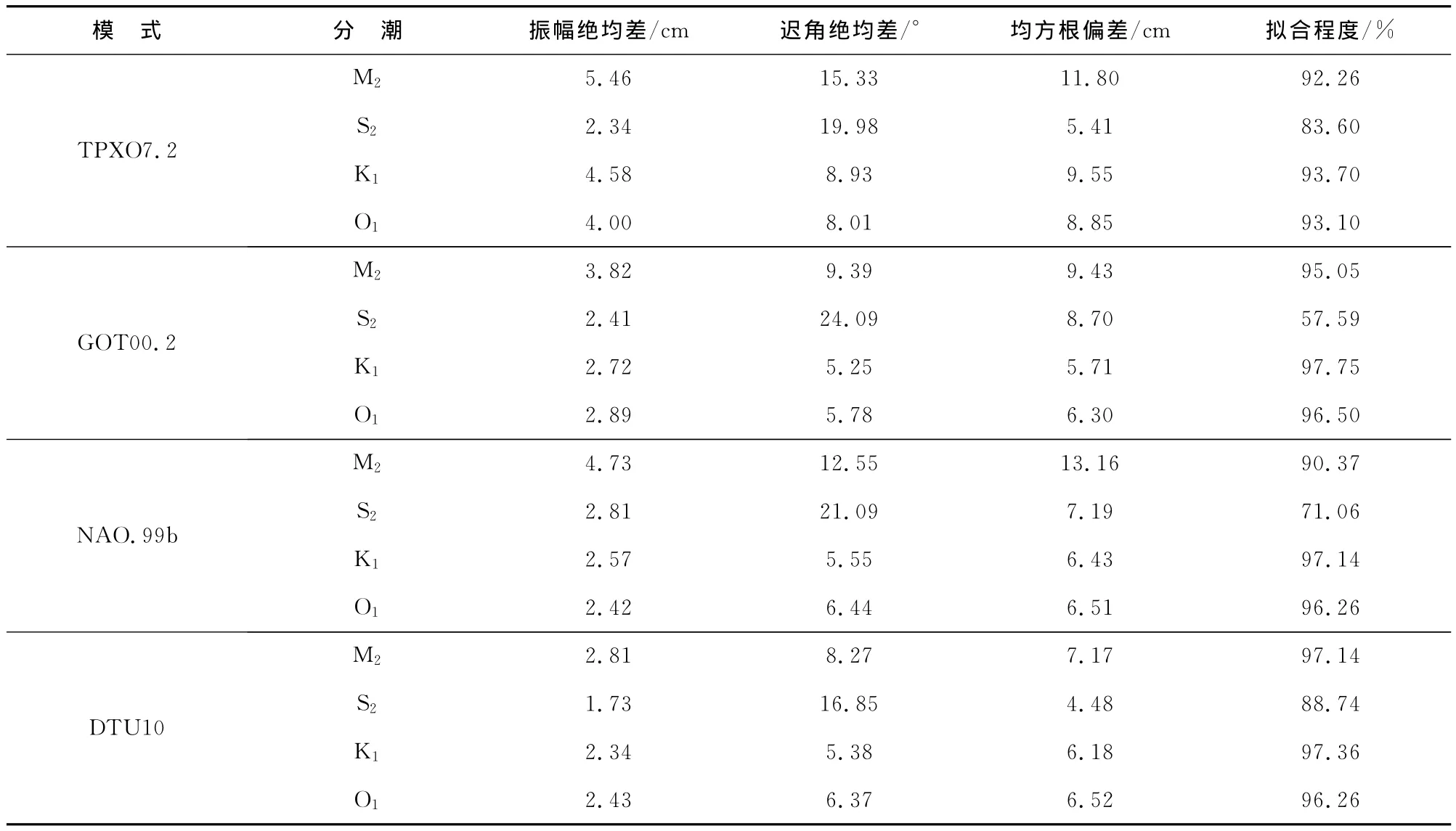
表4 与验潮站和T/P卫星轨道交叉点调和常数的对比Table 4 Comparison with the harmonic constants observed at the tidal gauge stations and the T/P crossover points
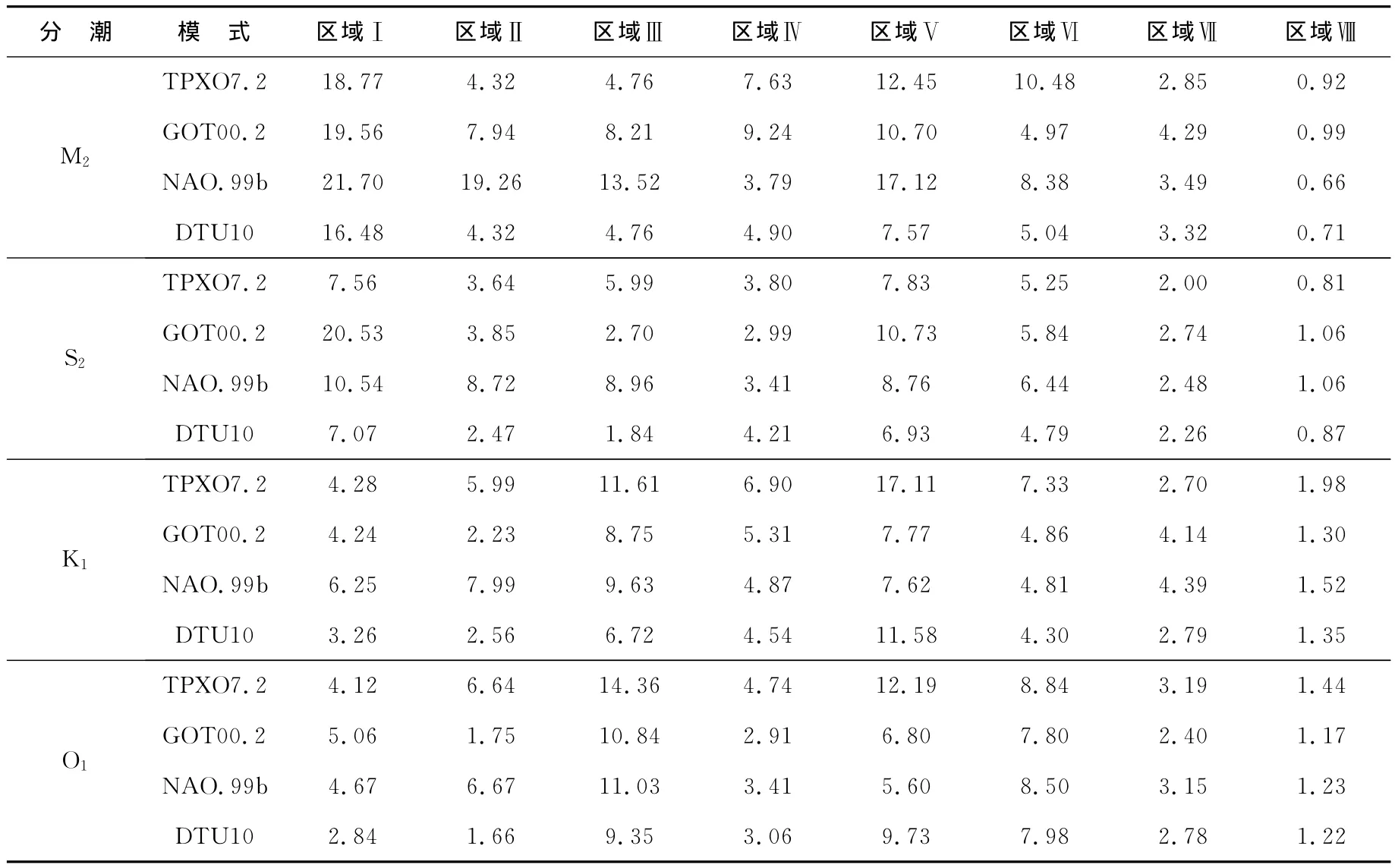
表5 分区域均方根偏差的对比(cm)Table 5 Comparison of root mean square deviations in different subareas(cm)
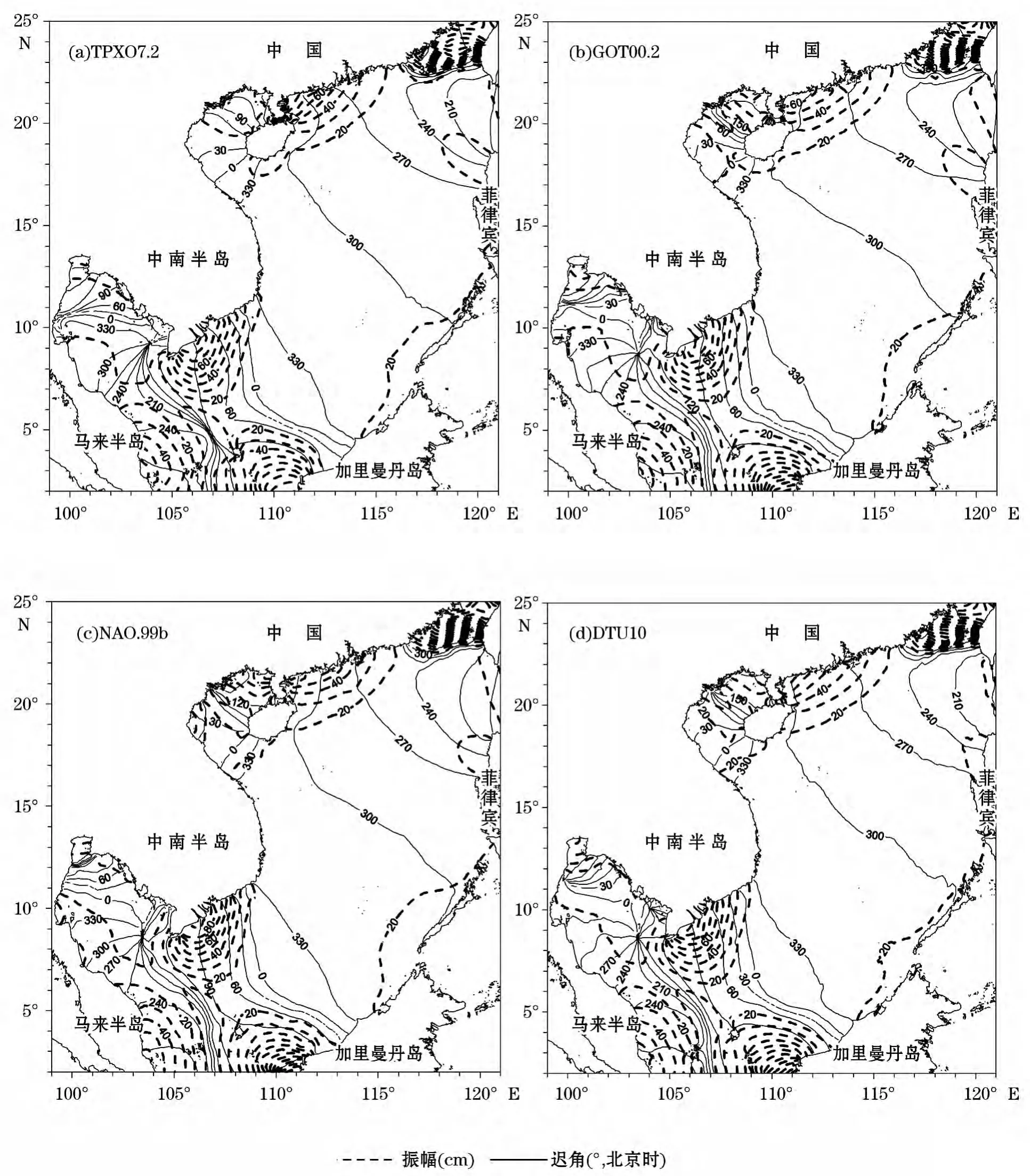
图2 不同全球大洋潮汐模式下的M2分潮同潮图Fig.2 Co-tidal charts of M2for different global ocean tide models
图3 不同全球大洋潮汐模式下的S2分潮同潮图Fig.3 Co-tidal charts of S2for different global ocean tide models
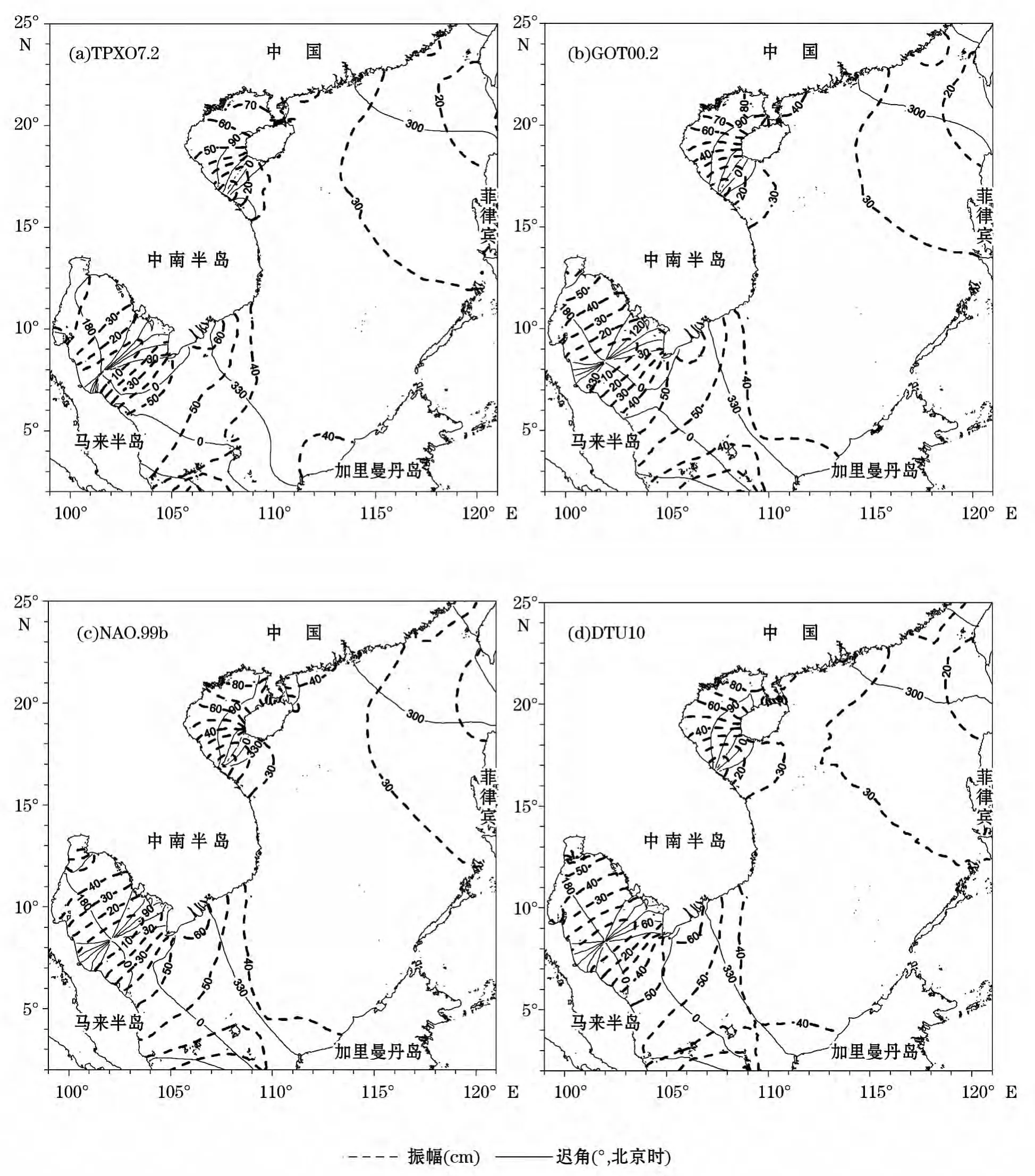
图4 不同全球大洋潮汐模式下的K1分潮同潮图Fig.4 Co-tidal charts of K1for different global ocean tide models
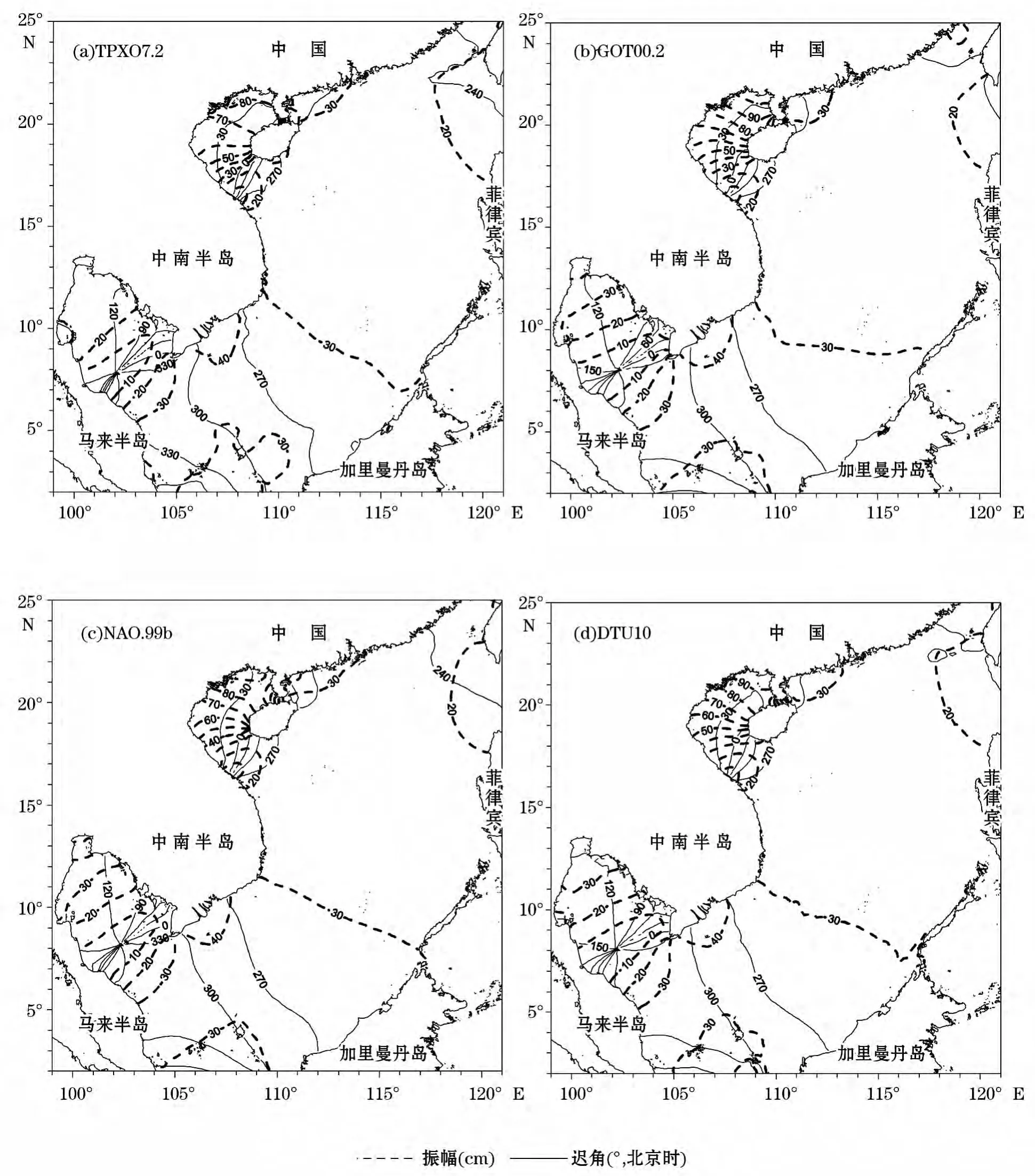
图5 不同全球大洋潮汐模式下的O1分潮同潮图Fig.5 Co-tidal charts of O1for different global ocean tide models
4 南海潮汐分布特征
根据第3节的准确度评估结果,分别利用图2b、3d、4d、5c来分析南海M2、S2、K1、O1四个主要分潮的潮汐分布特征。
由图2b可以看出,M2分潮潮波经吕宋海峡传入南海,部分潮波向北转入台湾海峡,大部向南海内部传播。在传播过程中,又有部分潮波转向西北进入北部湾,其主要部分则继续向西南传播,到达越南西南部附近海域时,部分潮波转向进入泰国湾,其余部分往南向巽他陆架海域传播。M2分潮在进入台湾海峡后与来自东海的潮波相遇,此处的等振幅线非常密集,这是由于来自东海的M2分潮振幅远大于来自南海的M2分潮振幅,在台湾海峡西北口的最大振幅超过了2m。M2分潮在南海北部广东沿岸最大振幅出现在湛江附近,可达0.8m。在北部湾传播过程中,M2分潮同潮时线的走向基本与湾轴垂直,在湾内有一个退化了的无潮点,北部湾内M2分潮的振幅很小,最大在湾顶0.4m左右。M2分潮在南海中部海域表现为驻波,同潮时线稀疏,振幅很小,基本在0.2m以内。M2分潮在泰国湾有两个潮波系统,一个无潮点位于泰国湾的顶端,同潮时线绕无潮点作逆时针方向旋转,另一个无潮点位于泰国湾湾口,呈顺时针旋转。
在南海大部分海区,S2分潮(图3d)的分布与M2分潮大体一致,只是振幅较M2分潮要小很多。
由图4d和5c可以看出,在南海,除了北部湾和泰国湾,K1分潮和O1分潮的潮波均从东北向西南传播。在泰国湾,K1分潮和O1分潮都有一个完整的逆时针方向旋转的潮波系统。在北部湾湾口,K1分潮和O1分潮各有一个退化了的无潮点。K1分潮和O1分潮都是在北部湾湾顶的振幅最大,都超过了0.8m。北部湾是我国近海全日分潮波最大的海区,这在世界上也不多见。对于一般海区,通常K1分潮的振幅大于O1分潮的振幅,而在北部湾恰好相反。这是由于北部湾的自由振荡周期更接近于O1分潮周期,使O1分潮潮波在北部湾产生共振,从而使得O1分潮的振幅增强[23]。
5 结语
本研究利用南海海域60个验潮站和22个T/P卫星高度计轨道交叉点处的调和常数资料,检验了四种全球大洋潮汐模式TPXO7.2、GOT00.2、NAO.99b和DTU10在南海的准确度。对比结果表明,四种全球大洋潮汐模式在南海均有较高的准确度,与卫星高度计资料比较的精度明显高于与沿岸验潮站资料比较的精度。为了更精确地给出四种大洋潮汐模式在南海不同区域的准确度,将南海分成了8个区,分别对比了四种大洋潮汐模式在各区域的准确度。北边界和东边界所在区域4个分潮都是DTU10结果最好,南边界所在区域M2和O1分潮GOT00.2的偏差最小,S2和K1分潮DTU10的偏差最小。在进行南海潮汐数值模拟选择开边界条件时,可以以DTU10模式为主,并利用GOT00.2模式作适当调整。最后简单分析了南海M2、S2、K1、O1四个主要分潮的潮汐分布特征。
(References):
[1]SCHWIDERSKI E W.Ocean tides,part I:Global ocean tidal equations[J].Marine Geodesy,1980,3:161-217.
[2]SCHWIDERSKI E W.Ocean tides,part II:A hydrodynamical interpolation model[J].Marine Geodesy,1980,3(1-4):219-255.
[3]SCHWIDERSKI E W.On charting global ocean tides[J].Reviews of Geophysics,1980,18(1):243-268.
[4]CARTWRIGHT D E,RAY R D.Oceanic tides from Geosat altimetry[J].Journal of Geophysical Research,1990,95(C3):3069-3090.
[5]LE PROVOST C,GENCO M L,LYARD F,et al.Spectroscopy of the world ocean tides from a finite element hydrodynamic model[J].Journal of Geophysical Research,1994,99(C12):24777-24797.
[6]LE PROVOST C,LYARD F,MOLINES J M,et al.A hydrodynamic ocean tide model improved by assimilating a satellite altimeter-derived data set[J].Journal of Geophysical Research,1998,103(C3):5513-5529.
[7]LEFEVRE F,LYARD F H,LE PROVOST C.FES98:A new global tide finite element solution independent of altimetry[J].Geophysical Research Letters,2000,27(17):2717-2720.
[8]LYARD F,LEFEVRE F,LETELLIER T,et al.Modelling the global ocean tides:a modern insight from FES2004[J].Ocean Dynamics,2006,56(5-6):394-415.
[9]EGBERT G D,BENNETT A F,FOREMAN M G G.TOPEX/POSEIDON tides estimated using aglobal inverse model[J].Journal of Geophysical Research,1994,99(C12):24821-24852.
[10]EGBERT G D,EROFEEVA S Y.Efficient inverse modeling of barotropic ocean tides[J].Journal of Atmospheric and Oceanic Technology,2002,19(2):183-204.
[11]MATSUMOTO K,TAKANEZAWA T,OOE M.Ocean tide models developed by assimilating TOPEX/POSEIDON altimeter data into hydrodynamical model:A global model and a regional model around Japan[J].Journal of Oceanography,2000,56(5):567-581.
[12]ANDERSEN O B,WOODWORTH P L,FLATHER R A.Intercomparison of recent ocean tide models[J].Journal of Geophysical Research,1995,100(C12):25261-25282.
[13]SCHRAMA E J O,RAY R D.A preliminary tidal analysis of TOPEX/POSEIDON altimetry[J].Journal of Geophysical Research,1994,99(C12):24799-24808.
[14]SHUM C K,WOODWORTH P L,ANDERSEN O B,et al.Accuracy assessment of recent ocean tide models[J].Journal of Geophysical Research,1997,102(C11):25173-25194.
[15]PENNA N T,BOS M S,BAKER T F,et al.Assessing the accuracy of predicted ocean tide loading displacement[J].J.Geod,2008,82(12):893-907.
[16]WANG Y H,FANG G H,WEI Z X,et al.Accuracy assessment of global ocean tide models base on satellite altimetry[J].Advances in Earth Sciences,2010,25(4):353-359.汪一航,方国洪,魏泽勋,等.基于卫星高度计的全球大洋潮汐模式的准确度评估[J].地球科学进展,2010,25(4):353-359.
[17]GLADKIKH V,TENZER R.A comparison of model estimates of ocean-tide loading displacements in New Zealand[J].Journal of Geodetic Science,2011,1(2):94-113.
[18]SAVCENKO R,BOSCH W.EOT10a-a new global tide model from multi-mission altimetry[J].Geophysical Research Abstracts,EGU General Assembly 2010,Vol.12,EGU2010-9624,2010.
[19]LI D W,LI J C,JIN T Y,et al.Accuracy estimation of recent global ocean tide models using tide gauge data[J].Journal of Geodesy and Geodynamics,2012,32(4):106-110.李大炜,李建成,金涛勇,等.利用验潮站资料评估全球海潮模型的精度[J].大地测量与地球动力学,2012,32(4):106-110.
[20]CHENG Y C,ANDERSEN O B.Multimission empirical ocean tide modeling for shallow waters and polar seas[J].Journal of Geophysical Research,2011,116(C11),C11001,doi:10.1029/2011JC007172.
[21]MUNK W H,CARTWRIGHT D E.Tidal Spectroscopy and Prediction[J].Philosophical Transactions of the Royal Society of London,Series A,Mathematical,Physical & Engineering Sciences,1966,259(1105):533-581.
[22]FANG G H,KWOK Y K,YU K J,et al.Numerical simulation of principal tidal constituents in the South China Sea,Gulf of Tonkin and Gulf of Thailand[J].Continental Shelf Research,1999,19(7):845-869.
[23]QIAO F L.Regional Oceanography of China Seas-Physical Oceanography[M].Beijing:China Ocean Press,2012:358-359.乔方利.中国区域海洋学——物理海洋学[M].北京:海洋出版社,2012:358-359.
