基于前车运动状态的运动学安全距离完善研究

2014-11-28马洪坤杨伟赵佳郝海彬

湖北汽车工业学院学报 2014年4期

马洪坤，杨伟，赵佳，郝海彬

（西华大学交通与汽车工程学院，四川成都610039）

近年来交通安全问题备受关注，资料显示，有70%至90%的交通事故是因为驾驶员操作不当造成的[1]。如果在事故发生前能够及时提醒驾驶员注意并在紧急情况下自动采取措施，对于减少交通事故作用明显，主动避撞系统即可实现这一功能。在汽车行驶过程中实时测量自车与前车的相对距离同时将实测距离与安全距离进行比较，一旦实测距离等于安全距离，立即报警提醒驾驶员注意同时采取相应的措施。

安全距离的确定是主动避撞系统功能实现的基础，目前国内外有大量关于安全距离模型的研究，主要有基于车间时距和基于车辆制动过程运动学分析的安全距离模型[2-4]。一般的安全距离模型通常主要考虑车辆当前的运动状态，往往不考虑车辆运动状态变化趋势对安全距离的影响。

笔者提出根据车辆的加速度大小及其变化率对车辆的运动状态进行判断，据此对基于制动过程运动学分析的安全距离模型进行补充完善，提高了模型的适应性和准确性，最后通过计算机仿真做了进一步验证。

1 车辆动力学模型

为了简化问题，只考虑车辆的纵向特性，假设路面平直，采用双轮车辆模型（图1）进行分析[5]。式（1）为整车运动方程，式（2）～（3）分别是前后车轮运动方程。

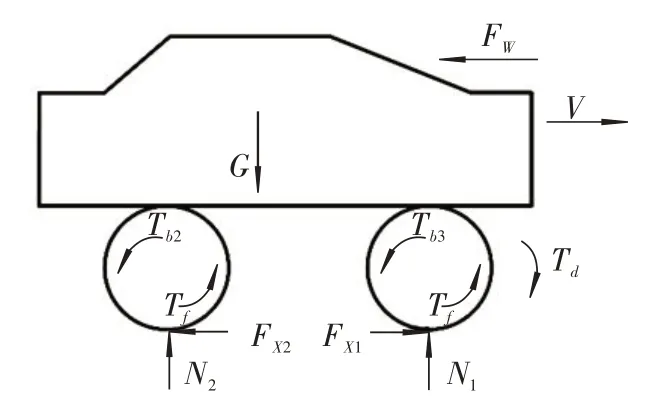
图1 双轮模型

式中：M为整车质量；V为车辆的加速度；μ为路面附着系数；N1，N2分别是前后车轮受到来自地面的法向作用力；J为车轮的转动惯量；R为车轮的滚动半径；12分别为前后车轮的角加速度；Tb1，Tb2分别是前后车轮的制动力矩；FW为空气阻力[6]。

2 传统运动学安全距离模型的不足

现阶段的安全距离模型大都是根据牛顿运动学原理衍生而来的，其模型的物理意义是前车和自车同时开始制动到停车，两车没有发生相撞。表达式[3]：

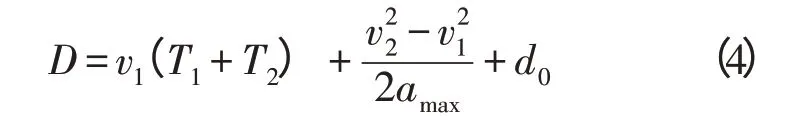
式中：D为安全报警距离；v1，v2分别为前车和自车的速度；T1为驾驶员反映时间；T2为制动器起作用时间；amax为车辆最大制动减速度；d0为停车后需保留的最小车间距离，取4m[3]。

该模型成立的前提条件为前车完全通过自身制动而停止，在计算安全距离时默认前车的最短制动距离为但是实际过程中前车有可能因为撞车而出现非正常停车，此时汽车的制动距离必然小于，因此根据传统的安全距离模型计算出的安全距离过小，不能达到避撞的目的，连环撞车事故就是由于前车出现非正常停车导致的，所以当前车出现非正常停车时，传统的运动学安全距离模型将失效。

如果前车完全通过自身制动停车，传统的运动学安全距离模型能够确保两车不相撞，但是该模型是在默认前车随时都可能采取制动的情况下计算安全距离，如果已经确定前车当前不会采取制动，该模型虽能够确保安全，但会导致安全距离过大，影响道路通过性。

因此，如果前车出现撞车该模型将失效，如果确定前车当前不会采取制动，该模型计算的安全距离过大，影响道路通过性。

3 前车运动状态判断

3.1 前车紧急制动

如果前车发生撞车，撞车前前车驾驶员必然意识到车辆处于危险状态，肯定会采取紧急制动，使车辆获得最大制动减速度amax，因此前车紧急制动是前车撞车的必要条件，可以根据前车的制动强度来判断前车是否会出现非正常停车。如果前车的制动减速度大于0.95amax，即可认为前车处于紧急制动状态，则可判断出前车有可能因为撞车导致非正常停车。

车辆的最大制动减速度

amax=φ0g

式中：φ0为当前路面的峰值附着系数。汽车在行驶过程中实时测量计算出前车的制动减速度，同时将前车制动减速度与0.95φ0g作比较，从而判断出前车是否处于紧急制动状态。考虑到不同路面的峰值附着系数往往不同，需要对汽车当前行驶的路面进行识别，从而得到当前路面的峰值附着系数。

3.2 前车持续加速

如果前车的加速度大于0，同时加速度变化率大于或等于0，则可认为前车驾驶员判断出当前路况良好，同时驾驶员的驾驶意图是要求车辆处于持续加速状态，也就是说前车当前不会采取制动，因此，可根据前车加速度及其变化率可判断出前车当前是否会采取制动。

4 路面识别

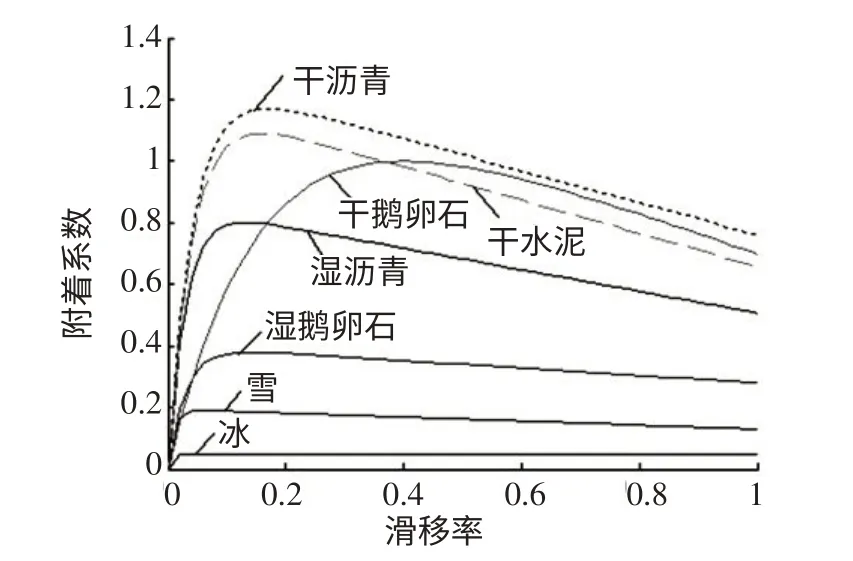
图2 典型路面的μ(s)曲线

如图2所示，当滑移率等于0.1时，除干沥青、干水泥以外的各典型路面的附着系数μ(0.1)差距明显，同时考虑到干沥青、干水泥2种路面附着特性相似，可合二为一。在Burckhardt轮胎模型下计算出各典型路面的μ(0.1)及峰值附着系数φ0，设计出不同路面的识别区间[7]，如表1所示。

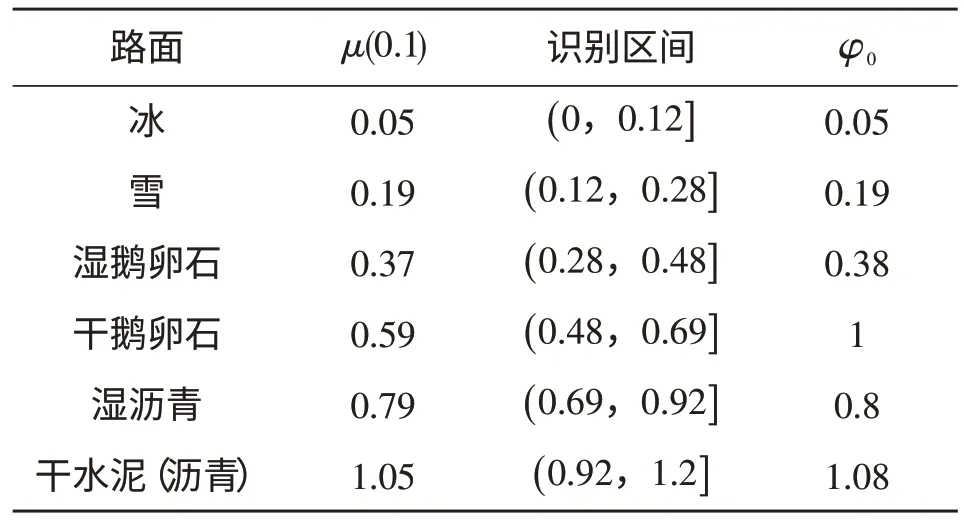
表1 各典型路面识别区间和峰值附着系数

汽车在驱动和制动工况下，车轮的运动学方程如式（6）～（7）所示：

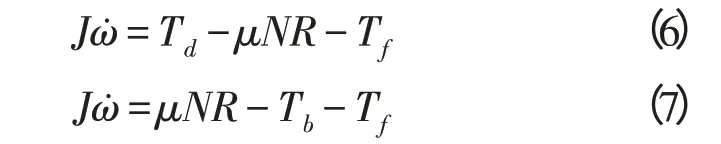
根据式（6）～（7）可估算出，汽车在行驶过程中，当前路面在滑移率等于0.1时的路面附着系数μ，同时判断其落入哪个识别区间[8]，从而完成路面识别，得到当前路面的峰值附着系数φ0，以便判断前车是否处于紧急制动状态。

5 完善后的安全距离模型

当前车紧急制动时，表示前车出现紧急情况，有撞车可能，则前车随时有可能出现非正常停车，为了确保安全，计算安全距离时应当将传统模型中前车的制动距离从调整为0，因此安全距离模型调整为

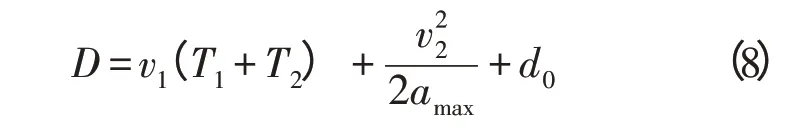
当前车持续加速时，即表示前车当前不会采取制动，因此只要能够确保自车制动到与前车速度相等的过程中两车没有相撞，即达到避撞目的。

自车制动到与前车速度相等所需最短时间：

此过程中前车行驶的最短距离为

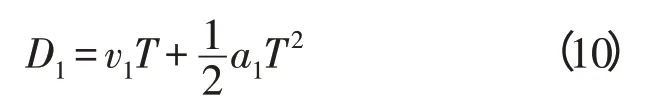
自车行驶的距离为

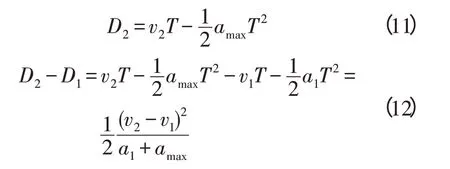
同时考虑到当前车速度v1大于自车速度v2时安全距离模型的适用性，安全距离调整为

式中：a1为前车的加速度。该模型物理意义是自车制动到与前车速度相等的过程中两车没有相撞。

当前车处于其他运动状态时，采用传统的运动学安全距离模型计算安全距离。

6 仿真试验

预设前车和自车分别以20 m·s-1和30 m·s-1的速度匀速行驶，初始车距为70 m，1s 后前车开始制动，当前车速度为7 m·s-1时发生撞车，前车非正常停车。如图3所示，完善前的安全距离模型没有达到避撞效果，5.46 s时实测车距为0，表示自车与前车相撞，由于前车非正常停车，安全距离模型失效。完善后的模型在前车处于紧急制动状态下调整安全距离，虽然前车非正常停车，但达到了避撞目的。

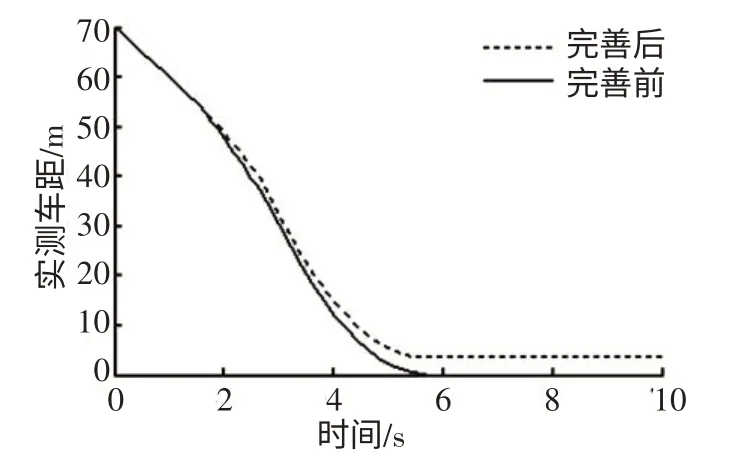
图3 前车紧急制动时实测车距—时间曲线

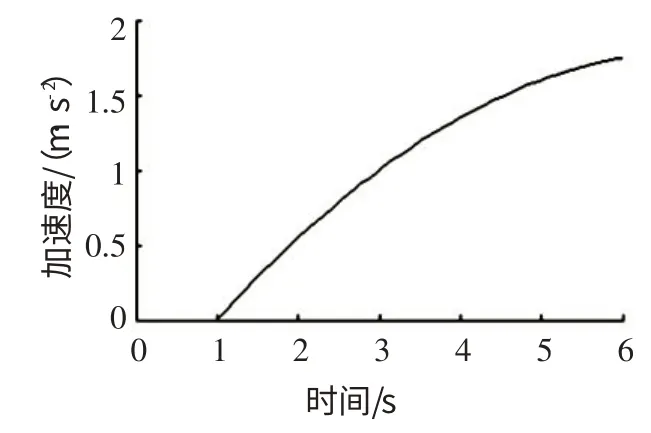
图4 前车加速行驶时加速度—时间曲线

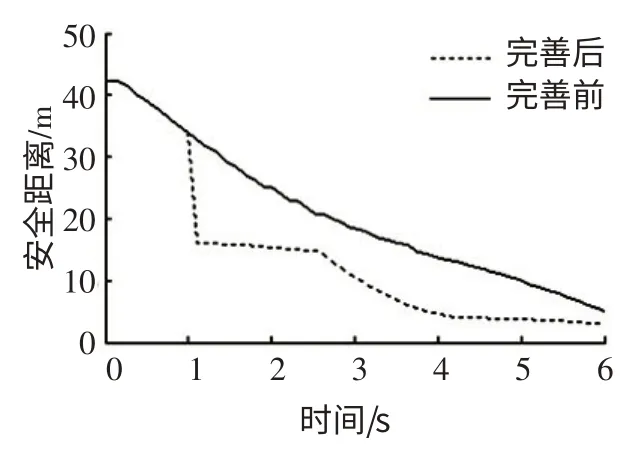
图5 前车加速行驶时安全距离—时间曲线

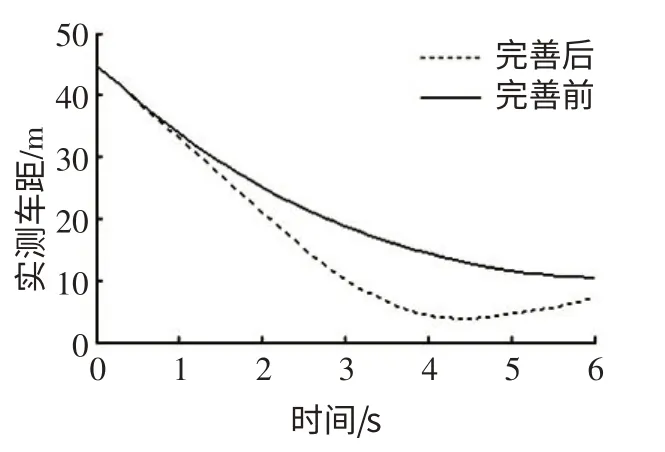
图6 前车持续加速时实测车距—时间曲线

预设自车以22 m·s-1的速度匀速行驶，前车以10 m·s-1的初速度匀速行驶1s 后开始加速行驶，如图4所示，其加速度和加速度变化率均大于0。初始车距为45 m，分别利用完善前和完善后的安全距离模型进行仿真。如图5所示，当前车匀速时，2种模型的安全距离相同，当前车加速行驶且加速度变化率大于0时，完善后模型的安全距离明显减小，在确保安全的同时可提高道路的通过性。如图6所示，完善前的安全距离模型虽能保证安全，但车距过大，道路通过性差，完善后的模型在保证安全的前提下缩短了车距，改善了道路通过性。