注采井间压力梯度计算与顶替段塞长度优化

王硕亮，李 垚，霍俊洲

（1.中国地质大学（北京）能源学院，北京100083；2.中国石油长庆油田分公司第六采油厂，陕西榆林718600；3.中国石油长庆油田分公司长南气田开发项目部，陕西榆林718600）

在调剖堵水过程中，在注入主剂段塞后，还需要注入一定体积的顶替段塞，将主剂顶替到油藏深部，顶替段塞一方面可以保障调剖堵水后油水井仍具有一定的注入采出能力，另一方面，也可以使主剂避开主要的压力降区域，增加主剂的有效作用时间。顶替段塞长度优化主要取决于注采井间压力梯度，然而目前中外关于注采井间压力梯度的计算方法多依靠主观经验，缺乏理论研究。

根据经典渗流理论［1］阐述，在均质储层条件下，大约有90%的压力降发生在油井周围23%的井网面积，这一理论只是一个定性规律，并没有严格的证明过程和定量化的计算方法。

苏延昌等利用人造非均质岩心，测定了注采井间压力梯度的变化规律［2］，由于测压点密度不够，未能准确描述出近井地带压力梯度变化情况。李宜坤等虽建立了顶替段塞长度的计算方法［3-4］，但该方法的假设条件过于理想化，并且没有研究堵剂进入地层后压力梯度的改变情况。为此，笔者从经典渗流理论入手，计算了调剖堵水前注采井间的压力梯度，应用有限元解法，计算了调剖堵水后的注采井间压力梯度，并通过改变地质条件和开发条件，分析了注采井间压力梯度的变化规律，并建立了最佳顶替段塞长度计算方法。

1 均质储层注采井间压力梯度计算

利用经典渗流理论，可计算出均质储层条件下的注采井间压力梯度。流体在水井与油井井底具有不同的流向，油井可以认为是汇，水井可以认为是源。假设流体为平面径向稳定流，其基本渗流方程［5］为

式中：p为地层压力，MPa；r为渗流半径，m。

经过分离变量、积分，在定边界条件下，可以求得

式中：pe为边界处地层压力，MPa；pwf为井底流压，MPa；re为供给半径，m；rw为井筒半径，m。

假设注采井距分别为300和480 m，改变注采压差，根据式（2）可以计算得到均质储层条件下注采井间的压力梯度（图1）。图1中x轴0点处对应的井间压力梯度为水井井底压力梯度，x轴最大处对应的井间压力梯度为油井井底压力梯度。从计算结果可以看出，解析方法与经典渗流理论的定性认识一致，压力梯度曲线呈现两端弯曲，中间平缓的形态，大部分压力降消耗在近井地带，距离井底10 m以内的区域，压力梯度较大；当注采压差分别为16，20和24 MPa时，计算结果曲线的形态变化不大，说明利用解析方法得到的井间压力梯度对注采压差与注采井距的变化不敏感，注采井间压力梯度拐点依然出现在距离井底10 m左右的区域。

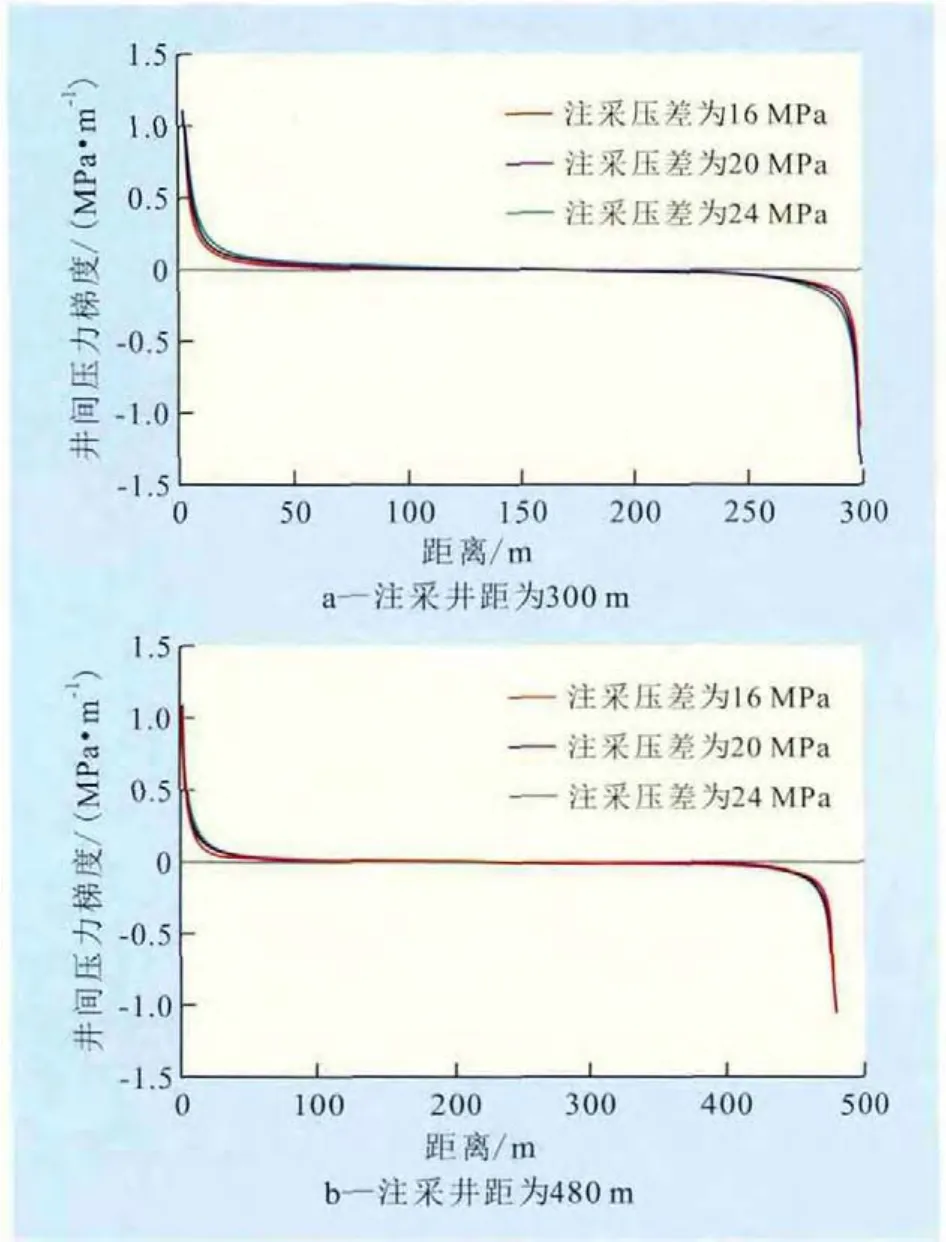
图1 不同注采井距下解析方法计算的注采井间压力梯度

2 存在窜流通道的注采井间压力梯度计算

上述解析方法的假设条件是均质储层，储层若存在注入水优势窜流通道，储层的非均质性很强，则该方法不适用于计算该条件下的压力梯度分布。为研究存在窜流通道情况下的注采井间压力梯度规律，利用有限元解法［6］，根据某油田实际情况，建立了典型数值模拟模型。在水井与油井之间设置1条高渗透条带，通过有限元数值模拟器计算，可以得到存在优势窜流通道情况下的注采井间压力分布（图2），其值为任意一点压力减去原始地层压力。由图2可以看出，注采井间存在窜流通道时的压力梯度与不存在窜流通道时的压力梯度分布规律相同，窜流通道并没有改变注采井间压力分布规律。

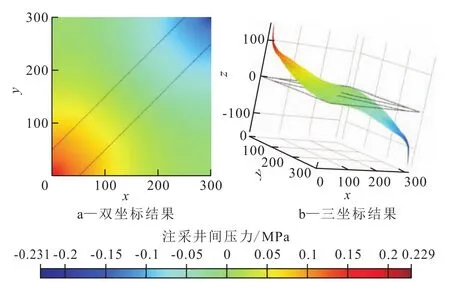
图2 存在优势窜流通道的井间压力分布

为了验证不同级别窜流通道对计算结果的影响，通过改变注采井间窜流通道的渗透率，计算得到不同级别窜流通道影响下的注采井间压力分布结果，以水井与油井连线为研究对象，对水井与油井连线上的压力进行计算并统计（图2），然后计算得到注采井间压力梯度（图3），通过结果可见，水井与油井间窜流通道的渗透率对注采井间压力梯度曲线形态并无明显影响。注采井间压力梯度拐点仍出现在近井地带10 m左右的区域。

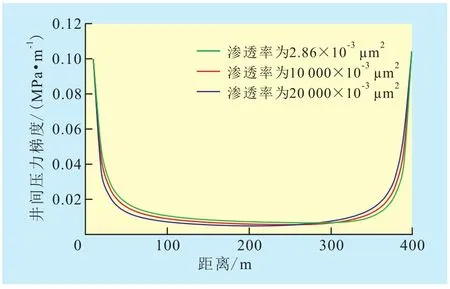
图3 存在优势窜流通道的注采井间压力梯度

3 封堵窜流通道后的井间压力梯度计算

堵剂进入储层后，窜流通道被封堵，储层的非均质性发生变化［7-8］，储层的压力分布和压力梯度分布也必然会发生变化，应用有限元模型，计算得到了水井调剖后的压力分布［9-10］（图4），其值为任意一点压力减去原始地层压力。从图4可以看出，当窜流通道封堵后，区域内的主要压力降不再产生于近井地带，而集中在堵剂两端。从水井到油井作一剖面，统计注采井连线的压力。由计算结果可知，主要的压力降集中在堵剂两端，注采井井底附近的压力不再是主要的压力降区域。这表明将堵剂主体段塞推进到地层深部后，并未降低堵剂主体段塞两端的压差。堵剂的封堵能力将是决定能否封堵窜流通道的重要因素。放大注采井底附近的压力曲线可以看到，对高渗透层进行封堵后，虽然近井地带不是油藏的主要压力消耗区域，但是，近井地带的压力曲线仍然存在拐点，且拐点的位置与前文所得结果一致，均为距离井底10 m左右的区域。

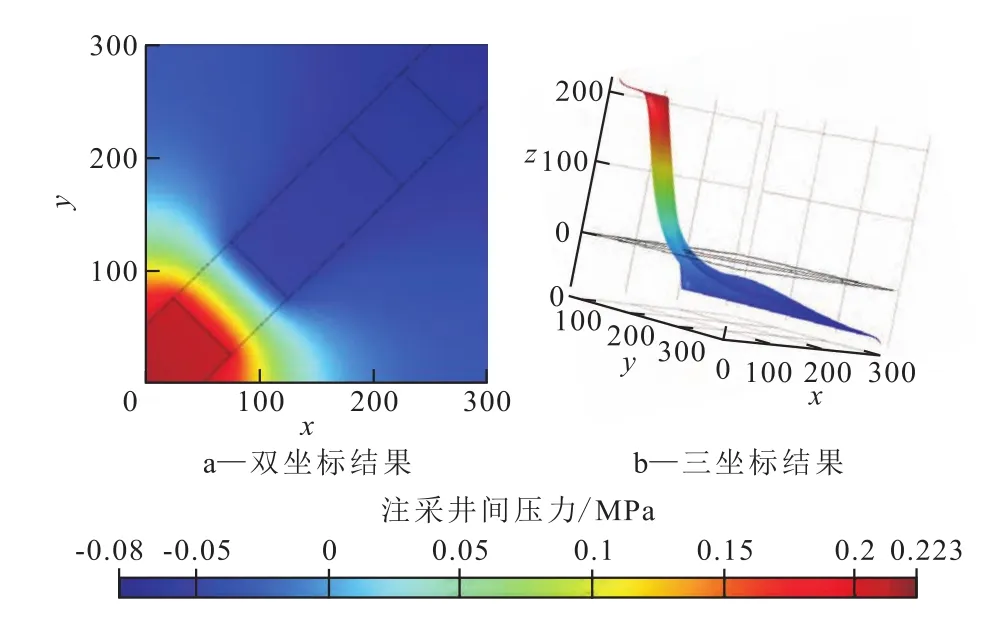
图4 水井调剖后注采井间压力分布

改变封堵方式，包括水井调剖、油井堵水、油水井双向封堵、深部调剖。每种封堵方式采用3种不同强度的堵剂。分析主要压力降区域和近井地带主要压力降区域。由计算结果（表1）可以看到，封堵方式改变后，井间的主要压力降区域仍然集中在堵剂两端，近井地带附近10 m范围内仍然是主要的压力降区域。

综上所述，采用解析方法和数值模拟方法，选用4种封堵方式，研究了调剖前和调剖后的井间压力梯度分布规律，发现调剖前后，近井地带的压力梯度曲线拐点均出现在距离井底10 m左右的位置，因此，为了达到保证封堵后油水井的最大生产能力和保护主力段塞的目的，建议在调剖堵水决策中采用长度为10 m左右的顶替段塞。

4 结论

采用解析方法，计算得到了均质储层条件下的井间压力梯度曲线，发现主要的压力降区域出现在近井地带10 m左右的区域内，且生产压差和注采井距对此结论的影响很小。

采用数值模拟有限元解法，计算得到了存在窜流通道情况下的注采井间压力梯度曲线，发现主要的压力降区域与解析法相同，出现在近井地带10 m左右的区域，并且，不同窜流通道的渗透率不会改变该结果；另外，计算得到了不同封堵方式情况下的注采井间压力梯度曲线，发现井间主要压力降集中在堵剂两端，近井地带的主要压力降区域出现在近井地带10 m左右的区域内。

以封堵后油井和水井生产能力最大化和保护主段塞为最优化原则，根据井间压力梯度计算结果，建议在调剖堵水决策中采用长度为10 m左右的顶替段塞。

［1］ 王晓冬.渗流力学基础［M］.北京：石油工业出版社，2006：31-35.

［2］ 苏延昌，于观宇.井间压力梯度变化规律研究［J］.科学技术与工程，2010，10（23）：5 734-5 737.

［3］ 李宜坤，赵福麟，周新宇，等.计算调剖堵水过顶替量的新方法［J］.油气田地面工程，2003，22（1）：10-15.

［4］ 李宜坤，赵福麟，张永军，等.压力梯度分布图的研究及应用［J］.江汉石油学院学报，2003，25（S2）：92-95.

［5］ 冯其红，王守磊，白军伟，等.层间非均质油藏提液效果数值模拟［J］.油气地质与采收率，2013，20（3）：49-52.

［6］ 廉黎明，秦积舜，杨思玉，等.二氧化碳驱数学模型研究进展及发展方向［J］.油气地质与采收率，2013，20（2）：77-82.

［7］ 姜汉桥，姚军，陈月明.胜二区沙二3封堵大孔道方案优化设计［J］.石油大学学报：自然科学版，1994，18（4）：90-94.

［8］ Murphy R P，Owens W W.The use of special coring and logging procedures for defining reservoir residual oil saturations［C］.SPE 3793，1973：841-850.

［9］ 李兆敏，张东，刘崴桂，等.冻胶泡沫体系选择性控水技术研究与应用［J］.特种油气藏，2012，19（4）：1-6.

［10］ 刘桂玲，张雅玲，李国华，等.变形三重介质低渗透油藏产能分析［J］.特种油气藏，2012，19（4）：61-64.