“熵增值”在试题质量分析中的应用
2014-11-28冯艳宾马洪超
冯艳宾 马洪超
“熵增值”在试题质量分析中的应用
冯艳宾 马洪超
难度和区分度是传统试题质量分析所采用的指标,而依据(难度,区分度)二维向量指标对试题质量进行排序需要主观权衡,从而造成了试题质量评判的不稳定性。基于此,根据信息熵理论,构建一种基于考生得分分布变化的客观试题质量指标“熵增值”。通过HSK阅读分测验的实证分析,“熵增值”的大小有效地反映了试题质量的优劣,其对应的难度和区分度指标符合经典测量理论的分析原则。最后采用模拟仿真的方式论证了“熵增值”和难度、区分度的相互影响关系。
试题质量;熵增值;难度;区分度
1 引言
通过率、区分度常常作为传统的题目分析指标。一般认为在经典理论中难度在0.3~0.7之间为好,难度为0.5最合适(谢小庆,1998)。在大规模考试中,难易试题均应保持在合理范围,例如,汉语水平考试HSK(初中级)试题在难易度分布上是由易逐步过渡到难,呈正态曲线分布。难度系数区间在0.1~0.9之间,难度值为0.4~0.6(<0.6)的中等难度题目最多(李慧,2000)。在经典理论中难度值为通过率,区分度的值则是采用鉴别指数法、积差相关或点二列相关计算获得的。区分度一般理解为题目具有区分不同水平考生的能力,区分度的含义因计算方法的不同而存在差异。理论上区分度取值范围为[-1,1],实际上区分度应为正值才有意义,一般认为区分度大于0.4时,题目才具有良好的鉴别能力。
项目反应理论中题目难度b的取值为项目特征曲线拐点在横坐标上的投影,其值与被试能力被统一在相同的尺度上;拐点处曲线的斜率为题目区分度,a值越大说明题目对被试的区分程度越高(冯艳宾和马洪超,2012)。项目反应理论中的难度值和区分度均依赖项目特征曲线拐点,以拐点的值作为整体指标,无法全面反映不同被试在试题上的作答情况。
在经典理论中,以通过率计算得来的题目难度值可能会掩盖具有一定能力的考生能全部答对,而能力较低的考生答对率低和高猜测的现象。这种“天花板效应”和“地板效应”意味着该题对部分被试失去意义。而用鉴别指数法计算出来的区分度只是区分高分组和低分数的能力,采用相关方法计算的区分度值也只反映题目得分和总体得分之间的相关关系。因此,以经典理论的难度值和区分度值来判定试题质量的好坏,可能会出现误断的情况,也即是说即使0.5难度值的试题,其质量也未必很好。
两种理论中的难度均为中间点的值来度量,而且难度和区分度因计算方法不同其含义完全不同,简单的难度值无法全面反映被试的整体反应状况。此外,经典理论的区分度和项目反应理论的区分度均无法全面体现试题对考生的鉴别功能。通过(难度,区分度)二维向量项指标来判定试题质量的优劣,需要依赖主观权衡,从而影响试题质量评判的效率,增加了评判结果的不稳定性。基于此,本研究以HSK数据为研究对象,采用“熵增值”来分析阅读测试中题目的质量,将传统的试题分析指标与熵增值进行比较,探讨“熵增值”在题目分析中的应用。
2 熵增值的原理
2.1 自信息和熵
在信息论中,熵表示的是不确定性的量度。信息论的创始人香农在其著作《通信的数学理论》中提出了建立在概率统计模型上的信息度量。其中自信息和熵是信息论中两个最基本的度量单位。在一个离散事件集合X,它含有N个事件:X={x1,x2,…,xn},事件xi出现的概率为pi,则事件xi的自信息为I(xi)=-logpi。自信息给出了一个随机事件未出现时所呈现的不确定性,同时它也度量了该事件出现后所给出的信息量。因此,事件自信息的大小也表明了它在该集合中所占的比重。即事件对集合X的自信息越大,它隶属于该集合的程度也就越高(Thomas M.Cover&Joy A.Thomas,2007)。

熵给出了集合X中各个事件未出现时所呈现的平均不确定性,也度量了集合X中一个事件出现时所给出的平均信息量。
2.2 熵增值
对于一个由n道0、1得分的试题构成的大规模考试来说,总成绩的所有可能分数为0~n分,总成绩分数的概率分布为P(X=i)=pi(i=0,1,…,n),总成绩分数的熵记为Hn;当增加一第n+1道0、1得分的试题时,总成绩的所有可能得分变成了0~n+1分,这时总成绩分数的概率分布为P(X=i)=(i=0,1,…,n+1),该分数集合的熵记为Hn+1,根据熵理论知Hn+1≥Hn。我们将熵的增加值Hn+1-Hn称作第n+1题相对于前n道试题的熵增值,简称第n+1题的熵增值。
3 熵增值的比较分析
3.1 熵增值与难度区分度的比较

由表1可知,第33题的熵增值最小,41题的熵增值最大。因为熵增值是一种动态的相对值,因而不同试题具有相同的熵增值。现根据熵增值的大小,选择两组试题,将试题的熵增值与经典理论和项目反应理论中试题参数进行比较。如表2、表3所示。
表2中的6道试题均为熵增值较低的题目,其中1、3、46题难度偏易且区分度低,27、49题难度偏难且区分度也低。根据经典测量理论的分析原则,偏难和偏易的题目都不是理想的试题。而33题难度虽然是中等,但区分度极低,依然不是理想试题。由以上数据我们看到,熵增值较小的试题在经典测量理论中的参数指标均不理想。同样,这几道试题在项目反应理论中的参数指标也均不理想。
表3中的题目在两种理论下的参数指标都很理想,其熵增值较大。综合表2和表3的数据可以看到,熵增值大时,试题质量较好,熵增值小时,试题质量较差。为展现不同熵增值试题的特征,给出熵增值最大的44题和熵增值最小的33题的考察熵增值较小试题的累计概率曲线,如图1所示。

表1 阅读测试试题熵增值(从小到大排序)
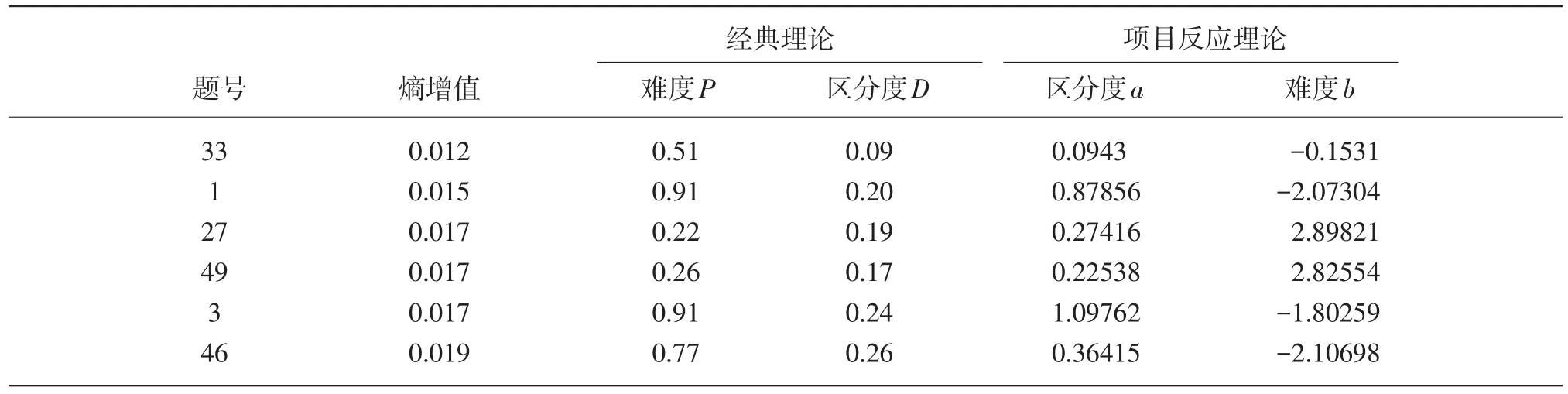
表2 熵增值较小试题的题目参数

表3 熵增值较大试题的题目参数

图1 熵增值最小最大试题累积概率曲线比较
图1中,33题熵增值最小,累积概率曲线在0分到25分的考生群体中呈增长趋势,但在25分到50分之间的考生群体中却没有继续增长,曲线趋于水平,这说明33题在25分到50分之间的考生群体,没有随着能力的提高而增加答对率,表明33题对水平比较高的考生没有鉴别力。而第41题,曲线渐进上升,说明随着考生能力的提高,答对率也逐步提高,在25分到30分之间的中等能力的考生群体上,答对率有显著提高,这与项目反应理论中的假设相一致,也符合我们直观的理解和常识。
3.2 熵增值与难度、区分度的关系
熵增值是一种相对值,是在总体分布的基础上,减少某一试题,形成新的分数分布。由于减少的某一试题与其他试题并不同质,因而对得分分布产生不同影响,使得不同得分分布的熵值发生变化,这种熵值的差称为某一试题的熵增值。
以下采用模拟仿真,对熵值与难度、区分度之间的关系进行分析。首先假定考试群体的能力分布为标准正态分布,考试试卷由6道0、1计分的试题构成,其中难度均为bi=0,区分度取ai=1(i=1,2,…,6,采用IRT中难度、区分度定义)。分三种情况来添加第7道题目:第一种情况,区分度和难度和前6道题一致,即b7=0,a7=1。第二种情况,区分度不变,而难度为2,即b7=2,a7=1。经计算,第一种情况下,总分分布的偏度SK=0,第7题的熵增值为ΔH(a=1,b=0)=0.2073。属于较难的试题。第二种情况下,总分分布出现右偏,该第7题的熵增值为ΔH(a=1,b=2)=0.137。看到ΔH(a=1,b=2)小于ΔH(a=1,b=0),这种熵增值差异是由试题的难度造成的(见图2)。

图2 试题难度对得分分布的影响
第三种情况,增加第7道题的难度为b6=0,区分度a6=0.5,这时总分的分布的峰度值增大,得分更加集中,计算得到第7题的熵增值为ΔH(a=0.5,b=0)=0.1732,小于ΔH(a=1,b=0)=0.2073。这种熵增值差异是由区分度不同造成的(见图3)。

图3 试题区分度对得分分布的影响
由图3可知,熵增值与试题自身的难度和区分度紧密相关,因为不同难度和区分度的试题会影响考生得分分布,从而导致熵的变化,它是参数指标的综合反映。在信息论中,熵是整个系统的平均信息量,是概率分布的函数。在能力考试中,考试分数的分布是研究试卷质量的基本指针之一,而考试分数分布的熵是反映考生能力和试题参数的一个综合指标。当试题的参数指标异常时,熵增值也会有相应的体现,能够体现考生群体对试题的全面反应。
4 小结
在经典测量理论和项目反应理论中,评判试题质量主要依靠难度和区分度。难度体现了考生总体对题目的作答的整体反映。区分度体现了考生不同能力部分考生作答差异的反映。传统的题目质量分析主要通过难度和区分度来进行评判,而在实践中要对题目质量优劣进行排序时,评判者需要综合考虑难度和区分度,形成一个主观判断,这在试题取舍时一方面会增大抉择的难度,另一方面也会带来评判结果的不稳定性。熵增值是在考生分数分布的基础上,通过调整某一试题,计算得来的,综合体现了难度和区分度对分数分布的影响,是一个综合指标,便于对考试试题质量进行排序,方便判断试题的优劣。
熵增值综合体现了试题难度和区分度,避免理论模型选择带来的误差,比如项目反应理论单、双、三参数logistic模型的题目参数均有差异,有些计算出来的试题参数与题目特征曲线并不拟合,有的甚至存在较大的偏差。熵增值与试题自身的难度和区分度紧密相关,当试题的难度和区分度异常时,熵增值也会有相应的体现,利用熵增值对试题进行甄别,能快速找出参数异常的试题。
另外,熵增值是基于得分分布计算出来的数值,应该考虑考生群体的代表性和测验的针对性;同时熵增值在大规模测试的试题质量分析效果比较明显,对于小规模考试,尤其是考生人数较少的测试,效果不明显。
[1]谢小庆.心理学讲义[M].武汉:华中师范大学出版社,1998.
[2]李慧.汉语水平考试(初中级)阅读理解命题中的效度考虑[J].汉语学习,2000(5):55-59.
[3]冯艳宾,马洪超.关于经典测量理论和项目反应理论中难度和区分度的探讨[J].中国考试,2012(4):10-14.
[4]Thomas M.Cover&Joy A.Thomas.信息论基础[M].北京:机械工业出版社,2007.
(责任编辑 周黎明)
Quality Analysis of Items Based on Increased Value of Entropy
FENG Yanbin and MA Hongchao
Difficulty and discrimination are traditional index in item analysis.To distinguish the quality of items and sequence the items basing on difficulty and discrimination need subjective weigh,so the instability of the items estimation cannot be avoided.So according to the information entropy theory,increased value of entropy is constructed as the index to measure the quality of items basing on the examinee score distribution.Through the empirical analysis of HSK reading test,the entropy value reflects the quality of items effectively;and they are consistent with the indexes in Classical Test Theory.In the end,It is showed that increased value of entropy is affected by difficulty and discrimination by using analog simulation.
Item quality;Increased Value of Entropy;Difficulty;Discrimination
G405
A
1005-8427(2014)11-0017-5
本课题为北京语言大学青年自主科研支持计划资助项目(中央高校基本科研业务费专项资金)项目批号:11JBB016;北京语言大学院级科研项目(中央高校基本科研业务专项资金资助),项目编号:14YJ030008。
冯艳宾,男,北京语言大学信息科学学院,讲师(北京 100083)
马洪超,男,北京语言大学汉语速成学院,讲师(北京 100083)
