计算机化自适应测验中几种常用能力估计方法的特性与评价
2014-11-28张心涂冬波
张心 涂冬波
计算机化自适应测验中几种常用能力估计方法的特性与评价
张心 涂冬波
该文介绍并比较了计算机化自适应测验(computerized adaptive testing,CAT)环境中的MLE、WLE、MAP、EAP等几种常用能力估计方法的发展演变以及各自的原理与特性,并对这些能力估计方法的发展脉络及其特性做了简要总结与评价,最后展望了未来CAT中能力估计的发展趋势。
计算机化自适应测验;项目反应理论;能力估计;参数估计
1 引言
长期以来在教育测量领域,传统纸笔测验(paper and pencil,P&P)形式简单,出题方便,易大规模实施,一直是测验的主要形式(van der Linden,2010)。20世纪80年代末以来,随着测量理论和计算机技术的发展,为使测验更加高效、公平和个性化,计算机化自适应测验(Computerized Adaptive Testing,CAT)逐渐发展了起来(毛秀珍,辛涛,2011;辛涛,乐美玲,张佳慧,2012)。CAT不再给定每个被试固定的测验,而是被试每做一题,计算机都会重新估计被试能力,并根据所估的新能力选择最适合被试的题目(van der Linden,2000)。CAT的施测项目少,效率高;项目的选择和评分更加灵活;测试结果能够更精确地反映被试的实际水平(罗芬,丁树良,胡小松,万宇文,甘登文,2003)。CAT的这些优点使得CAT成为很多大规模教育评估的首选(陈平,辛涛,2011)。
若要编制一套完整的以IRT为基础的CAT,需要进行以下六个方面的工作:确定采用的模型、建立题库、确定初始项目、确定选题策略、确定估计被试能力的方法以及确定测验终止的规则(Weiss&Kingsbury,1984)。能力估计在CAT中至关重要,能力估计的准确与否不仅影响选题策略的自适应选题,还会由此持续的影响CAT最关注的能力估计的准确性。CAT中的能力估计方法一般是基于IRT的。到目前为止CAT中常用的能力估计方法有极大似然估计(MLE)(Birnbaum,1968),极大后验估计(MAP)(Samejima,1969),期望后验估计(EAP)(Bock&Aitken,1981;Bock&Mislevy,1982),加权似然估计(WLE)(Warm,1989)等。然而,这些方法之间有何不同特性?在一个CAT中什么情况下应该选用何种方法最好?要回答这些问题,必须全面了解各种方法的原理、特性并深刻把握不同方法之间的相似和不同之处。对当前常用能力估计方法发展演变的探究与特性的评价不仅能够从理论上理清各种方法的来龙脉络,而且还能为CAT开发人员选择合适的能力估计方法起到向导的作用,具有重要的理论意义和实际意义。
2 CAT中能力估计方法的原理与特性
2.1 极大似然估计(Maximum Likelihood Estimation,MLE)
MLE广泛用于许多统计应用中的参数估计问题。Birnbaum(1968)采用了极大似然估计(MLE)方法来估计考生能力。不仅提出了2参数和3参数logistic模型下的似然函数作为潜在能力和已知项目参数的函数,而且还介绍了项目和测验信息函数的概念。
理论上,模型参数的似然函数包含了观察数据值所含所能反应的所有信息(Mislevy&Stocking,1989),因此,MLE在充分统计量存在时是一个充分统计量,而且其还拥有一些其他优良特性,例如渐进一致性和渐进正态性(Hambleton,&Swaminathan,1985)。因此,理想条件CAT下,当测验较长时,MLE是一种渐进无偏的能力估计方法(Warm,1989;Wang&Vispoel,1998)。但是,在实际中且测验较短时,MLE的偏差和误差相对较大,而且还可能出现无解的情况(Mislevy,1986)。根据Lord(1983;1986)的MLE偏差(Bias)公式:

由于以IRT为指导的CAT测验大大提高了测验效率,因此其测验大多较短,MLE法在较短测验中表现不佳迫使人们对其进行改进。对MLE的改进思路主要考虑了两个方向,其一是利用更多的先验信息减少误差,二是去除偏差项以减少偏差,根据这两个改进的思路,学者们后来分别开发出贝叶斯方法和加权似然方法。
2.2 极大后验估计(Maximum a Posteriori,MAP)
从利用信息的角度来看,MLE仅考虑了被试的作答数据中的信息。而随着大量测验的实施,人们从大量数据中发现被试的能力参数总是大致服从某种分布f(θ)。Samejima(1969)利用贝叶斯概率论,将这种先验的分布f(θ)引入了估计公式,提出了贝叶斯众数估计法(Bayes Modal estimator,BME)。由于其方法是直接将先验概率密度(一般取标准正态概率密度函数)乘以似然函数构建后验分布并求极大值,为了与期望后验估计区别,又称为极大后验估计(Maximum a Posteriori,MAP)(下文都以MAP代表BME方法)。作为一种替代MLE的方法,它与MLE的区别在于人们可以指定θ的先验分布f(θ)。
Lord(1986)表明MAP(以正态概率密度为先验)的偏差函数与MLE的偏差函数有如下关系:
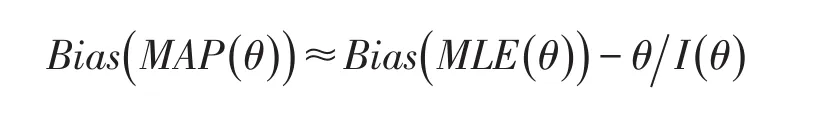
这里I(θ)是测验信息量。我们之前提到,MLE在项目较多时是一个渐进无偏的估计量,但在项目较少时MLE是有偏的(Hambleton&Swaminathan,1985)。Wang(1997)发现,当题库缺乏极端难度水平的题目时(这在真实题库中很常见),MLE也是有偏的,但偏差方向与贝叶斯方法相反。而这个式子表明MAP将一个与能力负相关的项加到了MLE的偏差中,这样会导致MAP在能力量表左端有正偏,右端有负偏,整体估计向先验均值的方向回归(Meijer&Nering,1999)。在题量较少的时候,MLE产生的向外扩张的偏差因此有可能会被MLE的向内收缩的偏差抵消一部分,但整体来看,MLE是一个渐进无偏估计,而MAP确属于有偏估计,在对整体无偏性要求较高的场合MAP并不适用(Eignor&Schaeffer,1995)。但是,实际中由于大量被试都集中于能力量表的中段,两端的人群较少,MAP利用了先验信息将估计的能力往量表中部“聚集”的效应,整体减小了对每个被试的估计误差。在一些更加注重控制随机误差的场合,如一些选拔性测验,MAP比MLE显示出了明显的优点。
由于标准正态分布较为集中,MAP会出现估计向先验均值回归的现象。然而MAP的先验分布并不一定必须是标准正态分布,还可以是均匀分布(在预先指定的θ值范围内)或者非信息先验密度(non-informative prior density),例如 Jeffreys先验(Jeffreys,1946)。Jeffreys先验是一个基于测验信息函数的先验概率,与信息函数的平方根成正比。即这样的估计称为JM估计量(Magis&Raîche,2012)。
从信息利用的角度看,在测验初期,似然函数并不能提供足够的信息,此时仅仅利用似然函数作为信息源的MLE方法无法有效的降低测验误差,而MAP法则将被试能力分布的先验信息引入估计,并将所有这些信息整合到后验分布中去。然后取后验分布概率最大的值作为能力估计值,缓解了测验初期信息不足的尴尬,从而实现了相对有效的控制测验的误差。
MAP作为早期的一种贝叶斯方法,它的最初目的是充分利用被试总体的能力的先验分布信息。对于利用贝叶斯理论构建的后验分布,最初采用后验分布的极大值而非均值,是因为后验分布一般是一个不规律的分布,当时还不了解该分布的均值该如何计算。而这个问题直到1982年Bock和Mislevy才以高斯—厄尔米特积分公式解决,由此他们也开发了一种新的方法——EAP(Bock&Mislevy,1982)。
2.3 期望后验估计(Expected A Posteriori,EAP)
在提出EAP法之前,Owen(1969,1975)曾提出过一种CAT的能力估计方法——Owen法。Owen法也是利用了贝叶斯的思想,该方法假设,每一次估计能力时,都通过将上一题的后验分布的均值和方差构建一个正态分布作为下一题的先验概率密度,由此连续估计,直到最后一题做完,获得一个最终的后验分布,其均值即为Owen连续贝叶斯估计量。由于以正态密度函数构建后验分布,后验分布的均值和方差变得容易计算(Owen,1975)。Owen法在当时由于其直接计算无须迭代在CAT能力估计领域曾一度非常流行(Wang&Vispoel,1998)。然而,节省计算资源的代价就是引入误差。Weiss和McBride(1984),利用理想题库和恒定的a参数模拟,发现OWEN能力估计通常会产生严重的偏差。而且Owen贝叶斯以不同顺序估计相同的题目会得出不同的结果。现在,人们在CAT中较少使用Owen法。然而,Owen法的出现说明在MAP出现后不久,人们已经想到要用后验分布的均值作为估计,只是当时还不知道如何计算一个无规律分布的均值,此外还说明,在多年以前,人们非常注重一个算法是否能够节省计算资源。
Owen法出现后不久,Bock和Aitken(1981)将视线转移到了能够对后验分布的均值和方差进行有效数值计算的积分公式,提出了期望后验估计(Expected A Posteriori,EAP)方 法(Bock&Mislevy,1982)。EAP方法是找到后验分布的均值和方差,直接以其均值作为能力估计值,标准差为误差。通过高斯积分公式,EAP估计变成了求和而不用迭代过程。这将简化繁琐的迭代计算,使得算法效率得到有效提高。
从理论上看,EAP不仅节省了计算资源,而且采用后验分布的均值,充分利用了整个后验分布的信息。这在测验初期非常具有实际意义。一般来说,测验初期由于信息不足,采用似然函数(或后验分布)极大值点处的值作为估计值会有不稳定的缺点。而采用整个后验分布的均值,可以有效地利用整个后验分布的形态提供的信息,稳定性相比MLE或MAP要高。而且从逻辑上看,EAP法直接考察实际的后验分布,这一点也优于Owen法。
EAP也属于贝叶斯方法,与MAP一样构建后验分布,因此对于能力的估计也会受先验分布的影响而产生与MAP类似的偏差,但与MAP不同的是,EAP考虑的是后验分布的均值,而MAP则考虑的是分布中的极大值点(众数)。EAP对后验分布采用数值积分,利用计算机可以直接计算,而MAP对整合了先验信息的似然函数为了求极大值点需要数值迭代。这是两种贝叶斯方法之间的主要区别。
EAP作为一种贝叶斯方法,加入了先验信息,其估计误差在多数情况下比MAP还要小,但对于能力值距离先验均值较远的被试,EAP做出的估计仍然是有偏的,其偏差方向与MAP一致,但相对略小于MAP的偏差。EAP除了不是一个无偏估计,拥有了大多数能力估计方法的优点,如估计值稳定,算法效率高,是目前经常采用的一种方法。例如我国的大型CAT,中国军人医学与心理选拔系统就采用了EAP作为能力估计方法。
针对EAP偏差较高的缺点,Wang(1997)利用四参数的贝塔分布作为先验提出了一种基本上无偏(Essentially Unbiased)的EU—EAP方法,并与MLE、WLE、MAP等方法进行了比较,结果表明该方法在有效降低了EAP偏差的同时,RMSE略有增加,基本上保留了EAP的低误差特性(Wang,et al.,1999)。
目前MAP和EAP是贝叶斯方法中最常见的两种。影响贝叶斯方法表现优劣的重要一点在于先验分布的选择。一般的经验是,被试的能力应该服从正态分布,故一般以正态分布作为先验。但是实际中正态分布往往并非最佳选择,而相对更分散的分布往往表现更好(Lord,1984;Warm,1989)。例如,有人认为贝叶斯方法的先验分布如果取标准正态分布,会对能力位于极端值附近被试的能力估计产生较大偏差,因此提出应该用其他分布作为先验分布,如二项分布,更有人甚至提出了这种经验分布的估计方法,其他的分布统称经验先验分布(Mislevy,1984;Wang.et al.,1999;殷华,宋继华,2005)。但也有人认为CAT能力估计之初应该使用比标准正态分布更加集中的分布,以确保最初的几道题的能力估计相对集中,降低整体估计误差,之后再逐渐使分布分散(简小珠,张敏强,2010)。
2.4 加权似然估计(Weighted Likelihood Estimation,WLE)
贝叶斯方法的考虑角度是引入被试的能力分布的先验信息,会帮助降低估计误差和均方差,但是其代价是提高估计偏差(Warm,1989;Wang.et al.,1999)。Warm(1989)从减少MLE偏差这个角度出发,从理论上探讨了MLE方法对于估计能力与题目难度有差异时的估计偏差,并提出修正这种偏差的加权似然估计方法。
Warm(1989)经过数学推导后认为,为了在似然方程中移除MLE的一阶偏差项,应该对似然函数乘以一个恰当的权函数w(θ)。在1PLM或2PLM中这个权函数就是测验信息函数的开方即而3PLM中,这个w(θ)多乘了一个与测验信息函数相关的指数,即Warm(1989)在文中提到,对于一个估计量来说,做到在局部区间偏差很小并不难,但是估计量更加应该注重在整个全局量表上的无偏性。WLE相比其他估计量在更加宽广的能力量表范围内接近无偏。
测验信息函数由所测题目的题目参数决定,从影响估计的因素看,影响估计准确性的因素不仅包括被试的能力分布,也包括测验题目对某一特定能力的被试所能提供的信息量。对被试信息量大的题目,相对来说应该是被试能力与题目难度相对匹配的题目。这种题目按照MLE的偏差公式误差相对较小,对其赋予较多权重显然有助于减少MLE整体的偏差。
相对于纸笔测验来讲,WLE偏差很低的优良特性在CAT中,尤其是题库完备的CAT中与MLE相比优势并不明显,因为随着CAT的进行,被试的能力很快就会与项目难度匹配,但是对于CAT的能力探查阶段,由于能力的估计还不是很准确,WLE还是有比较广阔的应用前景的。孙珊珊(2008)将WLE方法应用于早期阶段的CAT,并与传统的MLE做了比较,得出结论认为在早期阶段WLE各项指标都优于MLE,因而比MLE更适合用于CAT的早期阶段。
加权的思想可以推广到很多其他的应用上去,例如Tao,Shi,&Chang(2012)利用对不同项目进行不同加权的思想研究了混合测验的项目加权估计方法(Item-Weighted Likelihood Method)并在拓广的分部评分模型(GPCM)下与MLE和WLE做了比较,发现这种加权法相比MLE和WLE能够同时减少偏差和误差。
WLE从降低偏差的角度对MLE乘了一个加权函数,这种形式让人很容易就联想到之前介绍过的JM。这两种方法虽然概念上完全不同,JM是一个基于测验信息函数的有先验分布的贝叶斯估计,而WL是为了消除ML估计的偏差加了一个适当加权似然函数,但二者在形式上非常相似,尤其在单参数和两参数logistic模型下WLE的权函数就是JM的非信息先验。而三参数logistic模型下,先验分布稍有不同,WLE的信息函数多乘了一项与信息函数有关的指数,使得JM的能力估计值一般总是会大于WLE(Warm,1989 ;Magis,&Raîche,2012)。
3 CAT中常用能力估计方法的总结与评价
理论工作和实际研究都已揭示了MLE、EAP、MAP、WLE等估计方法的重要特性,从一般的研究结论来看,在这四种主要能力估计方法中,MLE误差(SE)最大,贝叶斯方法误差较小但却均向着先验均值有偏,WLE偏差最小。在贝叶斯方法中,EAP相比MAP偏差和误差均比较小。EAP的另一个优点就是无须迭代,计算效率高于MLE、WLE和MAP。MAP的主要优势在于变长测验中所需题目相比EAP更少,即测验效率更高。随着测验长度的增加,这些方法之间的误差区别越来越不明显。
对于以上介绍的几种方法,我们可以理出一条主线,即似然函数。上述几种方法都是围绕着似然函数进行。例如有的直接求似然函数的极大值(MLE),有的通过给似然函数加上先验信息(MAP、EAP),有的通过修正极大似然值的偏差(WLE)。虽然MLE,WLE与MAP看似属于不同方法,建立方法的初衷也各不一样,但就数学形式上,他们都能归结为综合权重乘以似然函数并求后验分布极大值的某种特殊形式。符合该形式的非贝叶斯估计量被统称为伪贝叶斯估计量(pseudo Bayes estimators)。由此可以看出,贝叶斯及伪贝叶斯众数估计量在更高的层面上被统一了起来(Ogasawara,2013)。
Warm(1989)指出,在CAT的能力估计领域,除了以上提到的几种基本的CAT能力估计方法,还有一些早期提出但已不太常见的其他方法本文未予 介绍,如 robustified jackknife(Waine&Wright,1980),h估计量(Jones,1982),以及双权估计(Bock&Mislevy,1981)。但总体而言,CAT的能力估计方法不如选题策略那么多。而且方法大多还是基于IRT的能力估计,简单的移植到CAT中来,并未考虑到CAT的特点。因此,基于CAT的特点,对能力估计方法进行革新,或许将成为CAT能力估计领域的新要求。为了实现上述目的,对当前CAT中主要能力估计方法的原理的深入理解,特性的总结归纳,以及对能力估计方法发展脉络的梳理有助于我们深刻把握不同时代CAT能力估计中所关注的问题,为将来方法上的创新扫清障碍。
4 问题与展望
4.1 问题
CAT的能力估计似乎总是无法同时满足偏差和误差的要求。一种方法,如果要想无偏,必然不能加入过多人为信息,但是如果想要误差较低,又不得不加入更多信息。在信息源一定的情况下,这两个要求从理论上形成了一个悖论。因此也导致了目前的方法大多只能求某一个指标表现较好。
4.2 展望之一MCMC方法
近年来计算资源越来越丰富而模型越来越复杂,利用吉布斯抽样理论对后验分布反复抽样的简便而耗时的MCMC也就进入了人们的视野。统计学家Albert(1992)首先将马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法应用到IRT参数估计研究中,大大简化了IRT中参数估计的复杂度,并且估计精度较好。但是MCMC作为一种反复抽样的算法,其算法效率比较低下(王权,2006)。未来的CAT模型越来越复杂,而计算资源越来越丰富,类似于MCMC这种比较耗费计算资源,但简单通用而且精度较高的估计方法可能会是一个流行趋势。
4.3 展望之二基于软计算的方法
基于软计算理论的人工神经网络(Artificial Neural Networks,ANNs)和遗传算法(Genetic Algorithm,GA)最近也被用于能力估计领域(余嘉元,2002;王祖俭,黄国兵,丁树良,2005)。此外,有人提出了遗传算法和神经网络结合起来估计的方法(王华,陈景,马翠琴,周丽娟,2012)。以上算法代表了近年来的能力估计的进展,由于大样本统计理论已经较为完善,因此上述方法在样本量比较小的时候优势较为明显。
4.4 展望之三针对CAT特点的优化
在能力估计方面,CAT与P&P最大的不同就是需要按照题目数量从少到多,对被试能力进行若干次估计。目前学界对CAT的能力估计的讨论大多沿用基于纸笔测验的IRT方法,即简单的将IRT中的能力估计方法移植到CAT中。并未考虑到CAT需要多次估计被试能力,且在CAT初期的题目样本量比较小而中后期样本量比较大的特点。
如果考虑到CAT的这种特点,或者可以尝试在不同的CAT阶段采用不同的方法。目前对各种能力估计方法的研究已经表明在不同的样本量具备不同特性(如MLE的大样本较好而小样本不好),那么研究针对CAT而进行专门优化的方法似乎也是一种可能的趋势。目前已经有一些研究涉及了这方面的问题(简小珠,张敏强,2010),但尚未出现专门论述这种不同阶段采用不同方法文献。
仅靠合理组合运用现有恰当方法并不能给CAT的能力估计的精度以质的突破,MCMC除了耗费大量的计算资源之外,所能获取的精度提升也非常有限,若要在CAT能力估计方法方面同时提高测验的误差与偏差,也许只有获取更多的信息源才能从根本上解决上述问题。
4.5 本研究的不足
本篇仅仅涉及了以IRT为指导的CAT的能力估计,以认知诊断为指导的CAT因篇幅有限而未涉及,此外本篇假设项目参数已知的能力的条件估计,对于项目参数是估计值的情况也未作讨论。本篇的结论是以单维CAT中的logistic模型下的结论为主,其他模型的结论因为篇幅原因也未在此讨论。
[1]陈平,丁树良,林海菁,周婕.等级反应模型下计算机化自适应测验选题策略[J].心理学报,2006,38(3):461-467.
[2]陈平,辛涛.认知诊断计算机化自适应测验中在线校准方法的开发[J].心理学报,2011,43(6):710-724.
[3]简小珠,张敏强.CAT初始阶段被试能力估计方法改进探究[J].心理科学,2010(6):1470-1472.
[4]罗芬,丁树良,胡小松,万宇文,甘登文.基于IRT若干参数估计方式的比较[J].江西师范大学学报(自然科学版),2003,27(1):56-60.
[5]毛秀珍,辛涛.计算机化自适应测验选题策略述评[J].心理科学进展,2011,19(10):1552-1562.
[6]孙珊珊.将WLE应用于早期阶段的计算机自适应测试[D].东北师范大学,2008.
[7]王华,陈景,马翠琴,周丽娟.基于GA-BP算法的IRT模型参数估计方法研究[J].华北电力大学学报(自然科学版),2012,39(5):109-112.
[8]王权.“马尔可夫链蒙特卡洛”(MCMC)方法在估计IRT模型参数中的应用[J].考试研究,2006,2(4):45-63.
[10]王祖俭,黄国兵,丁树良.基于遗传算法的项目反应理论3PLM参数估计[J].江西师范大学学报(自然科学版),2005,29(6):475-477.
[11]辛涛,乐美玲,张佳慧.教育测量理论新进展及发展趋势[J].中国考试,2012(5):3-11.
[12]殷华,宋继华.CAT能力求解算法研究与优化[J].中国人民公安大学学报(自然科学版),2005,44(2):59-61.
[13]余嘉元.基于联结主义的连续记分IRT模型的项目参数和被试能力估计[J].心理学报,2002,34(5):522-528.
[14]Albert,J.H.Bayesian estimation of normal ogive item response curves using Gibbs sampling[J].Journal of Educational Statistics,1992,17(3):251-269.
[15]Birnbaum,A.Some latent ability models and their use in inferring an examinee's ability[M].In F.M.Lord&M.R.Novick,Statistical theories of mental test scores.Reading,MA:Addison-Wesley.1968:392-479.
[16]Bock,R.,&Aitkin,M.Marginal maximum likelihood estimation of item parameters:Application of an EM algorithm[J].Psychometrika,1981,46(4):443-459.
[17]Bock,R.,&Mislevy,R.J.Adaptive EAP estimation of ability in a microcomputer environment[J].Applied Psychological Measurement,1982,6(4):431-444.
[18]Chen,S.,Hou,L.,&Dodd,B.G.A comparison of maximum likelihood estimation and expected a posteriori estimation in CAT using the partial credit model[J].Educational And Psychological Measurement,1998,58(4):569-595.
[19]Eignor,D.R.&Schaeffer,G.A.Comparability studies for the GRE General CAT and the NCLEX using CAT[M].Paper presented at the meeting of the National Council on Measurement in Education,San Francisco,April 1995.
[20]Jeffreys,H.An invariant form for the prior probability in estimation problems[M].Proceedings of the Royal Society of London.Series A,Mathematical and Physical Sciences,1946:186,453-461.
[21]Jones,D.H.,&Educational Testing Service,P.J.Redescending M-Type Estimators of Latent Ability[J].Program Statistics Research,Technical Report No.1982:82-30.
[22]Lord,F.M.Applications of item response theory to practical testing problems[M].Hillsdale,NJ:Lawrence Erlbaum.1980.
[23]Lord,F.M.Unbiased estimators of ability parameters,of their variance,and of their parallel-forms reliability[J].Psychometrika,1983,48(2):233-245.
[24]Lord,F.M.Maximum likelihood and Bayesian parameter estimation in item response theory(Research Rep.No.RR-84-30-ONR)[M].Princeton,NJ:Educational Testing Service.1984.
[25]Lord,F.M.Maximum likelihood and Bayesian parameter estimation in item response theory[J].Journal of Educational Measurement,1986,23(2):157-162.
[26]Magis,D.,&Raîche,G.An iterative maximum a posteriori estimation of proficiency level to detect multiple local likelihood maxima[J].Applied Psychological Measurement,2010,34(2):75-89.
[27]Magis,D.,&Raîche,G.On the relationships between Jeffreys modal and weighted likelihood estimation of ability under logistic IRT models[J].Psychometrika,2012,77(1):163-169.
[28]Meijer,R.R.,&Nering,M.L.Computerized adaptive testing:Overview and introduction[J].Applied Psychological Measurement,1999,23(3):187-194.
[29]Mislevy,R.J.,&Brock,R.Biweight estimates of latent ability[J].Educational And Psychological Measurement,1982,42(3):725-737.
[30]Mislevy,R.J.Estimating latent distributions[J].Psychometrika,1984,49(3):359-381.
[31]Mislevy,R.J.Bayes Modal Estimation in Item Response Models[J].Psychometrika,1986,51(2):177-95.
[32]Mislevy,R.J.,&Stocking,M.L.A consumer's guide to LOGIST and BILOG[J].Applied Psychological Measurement,1989,13(1):57-75.
[33]Mislevy,R.J.Some formulas for use with Bayesian ability estimates[J].Educational and Psychological Measurement,1993:53,315-328.
[34]Ogasawara,H.Asymptotic properties of the Bayes and pseudo Bayes estimators of ability in item response theory[J].Journal of Multivariate Analysis,2013:114,359-377.
[35]Owen,R.J.Tailored Testing[M].Research Bulletin,Princeton,N.J.:Educational Testing Service,1969:69-92.
[36]Owen,R.J.A Bayesian sequential procedure for quantal response in the context of adaptive mental testing[J].Journal of the American Statistical Association,1975(70):351-356.
[37]Samejima,F.Estimation of latent ability using a response pattern of graded scores[J].Psychometrika Monograph Supplement,1969:34(4,Pt.2).
[38]Samejima,F.A comment on Birnbaum's three-parameter logistic model in the latent trait theory[J].Psychometrika,1973,38(2):221-233.
[39]Tao J.,Shi N.-Z.,Chang H.-H.Item-Weighted Likelihood Method for Ability Estimation in Tests Composed of Both Dichotomous and Polytomous Items[J].Journal of Educational and Behavioral Statistics,2012,37(2):298-315.
[40]van der Linden,W.J.&Glas,C.A.W.(Eds.).Computerized adaptive testing:Theory and practice[M].Boston:Kluwer.2000.
[41]van der Linden,W.J.&Glas,C.A.W.(2Eds.).Elements of Adaptive Testing[M].New York,NY:Springer.2010.
[42]Wang,T.Essentially unbiased EAP estimates in computerized adaptive testing[M].Paper presented at the annual meeting of the American Educational Research Association,Chicago IL.1997.
[43]Wang,T.,&Vispoel,W.P.Properties of ability estimation methods in computerized adaptive testing[J].Journal of Educational Measurement,1998,35(2):109-135.
[44]Wang,T.,Hanson,B.A.,&Lau,C.A.Reducing bias in CAT trait estimation:A comparison of approaches[J].Applied Psychological Measurement,1999,23(3):263-278.
[45]Warm,T.A.Weighted likelihood estimation of ability in item response theory[J].Psychometrika,1989,54(3):427-450.
[46]Weiss,D.J.,&Kingsbury,G.Application of computerized adaptive testing to educational problems[J].Journal of Educational Measurement,1984,21(4):361-375.
[47]Weiss,D.J.,&McBride,J.R.Bias and information of Bayesian adaptive testing[J].Applied Psychological Measurement,1984,8(3):273-285.
Properties and Evaluations of Several Ability Estimations Widely Used in Computerized Adaptive Testing
ZHANG Xin and TU Dongbo
This article introduced the principle and properties of several ability estimator widely used in computerized adaptive testing environment,such as MLE,WLE,MAP&EAP etc.And then,we summed up and appraised the developmental features and properties of these methods.Finally,we try to make several outlooks with regard to the tendency of ability estimation used in Computerized adaptive testing.
Computerized Adaptive Testing;Item Response Theory;Ability Estimation;Parameter Estimation
G405
A
1005-8427(2014)05-0018-8
张 心,男,江西师范大学,硕士研究生(南昌 330022)涂冬波,男,江西师范大学,副教授(南昌 330022)
