基于统计推断的电子设备突发故障预测方法研究❋

姚云峰 李绅政

（1.92419部队 兴城 125106）（2.92493部队 葫芦岛 125000）

1 引言

设备的故障通常是由其内在失效机理与外部环境因素综合作用导致的，这是一个复杂的过程，但是从故障的发展进程来看，设备的故障可分为突发故障与退化故障两种［1～6］。突发故障表现为设备监测参数的测试数据在储存过程中一直保持在某一合格范围内，但在某一时刻突然超出规定阈值［7～8］。

对于电子设备的健康状态信息，最为重要的是监测数据，它表征了电子设备的健康状态，且具有一定的规律性［8］，因此对储存状态下的整批电子设备进行突发故障预测时，可在一定置信度的前提下，采用抽样的方法，根据样本的监测数据（主要是故障数据）对总体的分布进行统计推断，确定其分布规律，进而根据监测数据的分布规律研究电子设备的突发故障预测模型。

2 故障数据分布类型

对于储存状态下的整批电子设备，其故障数据可表现为设备出现故障的时间。由于设备在某一时刻可能发生故障也可能不发生故障，其故障时间是一个随机变量，因此对于故障时间t，可以构造一维分布F（t，α）（其中α＝（α1，α2，…，αk），是该分布的参数向量），且其一维密度函数f（t，α）存在，则

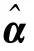
对于电子设备的故障数据，根据工程经验通常假定其服从指数分布，分布密度函数可表示为

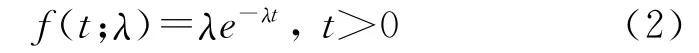
式中λ为设备的平均故障率，此时故障数据分布参数向量α＝（λ）。由指数分布的性质可知，平均故障率λ和平均寿命θ互为倒数。

3 故障数据分布的统计推断

3.1 故障数据分布参数极大似然估计

如果根据工程经验对故障数据的分布类型进行了假设，可以认为故障数据的分布类型是已知的，只是分布的参数未知，这样就可以根据样本的数据对总体的分布参数进行估计，这就是数理统计中的参数估计问题。为了确定分布参数的估计量，可以采用极大似然估计法［9］。

对于抽样的一批电子设备，由于采用修复性维修，因此每次测试时样品的总数是不变的，可看作是有替换的定时截尾试验［10］。假设对抽样的n个设备进行了m 次测试，每次测试时设备的故障数为ri（i＝1，…，n），则设备的总测试时间为n个设备测试m次的时间，可表示为

平均寿命θ的极大似然估计为

如果电子设备的故障时间（平均寿命）服从指数分布，则故障率λ的极大似然估计量可表示为

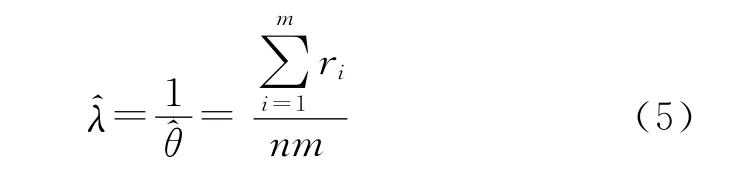
3.2 故障数据分布拟合检验

对于故障数据，根据工程经验假定其可能分布类型后，还需要对其进行假设检验，以验证假设是否成立。假设检验分为参数检验和非参数检验，当总体分布类型已知，只对某些参数的假设进行的检验称作参数检验，对其他假设作出的检验称作非参数检验［9］。由于设备故障数据的分布类型未知，本文根据工程经验对其假设，并利用样本数据进行检验，因此属于非参数假设检验。

判断总体是否为某种分布（如正态分布）的检验，统称为分布的拟合优度检验，简称分布拟合检验。常见的分布拟合检验有χ2分布拟合检验和KS拟合检验。当总体为一维且理论分布完全已知时，Копмогоров检验优于χ2检验［9］，因此本文采用Копмогоров检验法，简称 K检验。

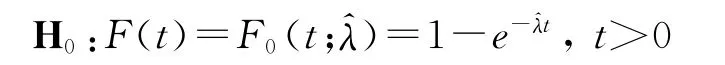
同样可取检验统计量

其中

（T（1），T（2），…，T（p））是（T1，T2，…，Tp）的顺序统计量。当样本中有重复数据时，可参照文献［9］计算。

为提高检验功效，Finklestein和Schafer提出检验H0的统计量

并针对不同的显著性水平α，确定了S＊n的临界值表。

显然，di（i＝1，…，n）的值大，的值也大，此时分布函数的曲线与经验分布函数Fn（t）拟合得不好，应拒绝H0。所以对于显著性水平α，检验的规则是：若时，拒绝H0，否则就接受H0。

4 突发故障预测模型

随着储存时间的增加，电子设备可能会发生突发故障。由于突发故障发生时间短且故障前无明显征兆，无法根据监测参数的历年测试数据对其进行预测［4］，因此可以考虑基于故障数据来统计分析其故障规律。通过对电子设备历年测试信息的整理，发现其故障数据均表现为设备出现突发故障的时间，因此可以根据统计推断得到的故障数据分布函数，对电子设备的突发故障进行预测，此时故障数据的分布参数是一个不随时间变化的常数。根据故障密度函数的定义，电子设备在0～t时间段内发生突发故障的概率即为该时间段内突发故障密度函数下所围的面积，如图1中阴影部分所示。

图1 突发故障密度函数曲线

设电子设备突发故障密度函数为f（t，α），T为设备突发故障前时间，则电子设备在0～t时间段内发生突发故障的概率为

如果要预测电子设备在t～t＋Δt（Δt＞0）时间段内的突发故障概率，则是一个条件概率事件，即在0～t时间段内设备没有发生突发故障的条件下，对t～t＋Δt时间段内设备发生突发故障的概率进行预测，此时电子设备的突发故障概率为

如果电子设备的突发故障时间服从指数分布，则突发故障密度函数可表示为f（t，α）＝λe－λt，t＞0，由式（8）和式（9）可知，电子设备在0～t时间段内发生突发故障的概率为F1（t）＝P（T≤t）＝1－e－λt，在t～t＋Δt时间段内发生突发故障的概率为F1＊（t）＝P（t＜T≤t＋Δt｜T＞t）＝1－e－λΔt，即电子设备在任意Δt时间间隔内发生突发故障的概率等于在0～Δt时间段内发生突发故障的概率，这体现了指数分布的无记忆性。

综上所述，对电子设备进行突发故障预测时，由于基于故障数据得到的分布参数向量为一确定值，不随时间变化，因此只需对设备的故障数据进行统计推断，确定其突发故障密度函数，即可根据式（8）和式（9）对设备的突发故障概率进行预测，电子设备故障预测流程如图2所示。

图2 电子设备突发故障预测流程

5 实例分析

以某单位储存状态下整批电子设备为研究对象，随机抽取10个设备作为样本进行分析。由于该批设备采取定期检测方式，从2006年开始，每年测试一次，测试信息记录到2013年，因此可以根据2006年到2011年的监测数据，对设备2012年和2013年的突发故障概率进行预测，并将预测结果与实际故障情况进行对比，检验突发故障预测模型的适用性。

根据工程经验，可以假定电子设备的故障数据服从指数分布。通过对设备2006年到2011年故障数据进行整理，发现抽取的10个设备在2007年到2011年测试时发生故障且均为突发故障，故障个数分别为1，1，1，2，2。由于对该批设备进行定期测试，每年测试一次，如果以年为时间单位，则设备的突发故障时间可表示为2，3，4，5，5，6，6。设电子设备的故障数据为T，要检验T是否服从指数分布，即检验假设 H0：T～F（t；λ）＝1－e－λt，t＞0是否成立。

由式（5）可得电子设备故障数据分布参数向量λ的极大似然估计量为

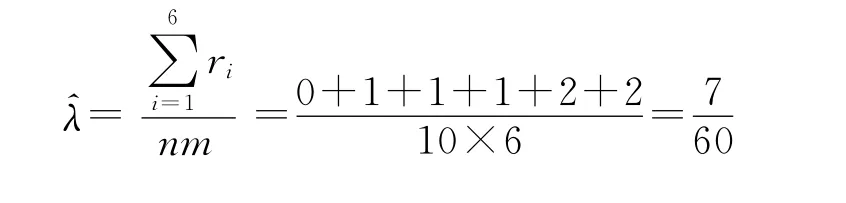
将设备的故障数据按从小到大的顺序排列（重复的数据合并为一个），对其进行 Копмогоров检验，计算过程如表1所示。

表1 设备故障数据的指数分布检验

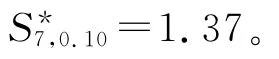
由于λ是一个常数，不随时间变化，因此根据式（9）即可对该批电子设备2012年和2013年的突发故障概率进行预测。由指数分布的无记忆性可知，设备在2012年发生突发故障的概率即为2011年和2012年测试时间间隔（1年）内发生突发故障的概率，即

同理2013年发生突发故障的概率为

查阅该批电子设备2012年和2013年的测试记录，可知2012年和2013年测试时均有一个设备出现突发故障，因此本文建立的电子设备突发故障预测模型是合理的。由于电子设备每年发生突发故障的概率不变，因此需将强对设备的维护保养，尽量减少储存状态下健康状态退化造成的故障。

6 结语

本文在一定置信度的前提下基于故障数据的统计分布规律对电子设备突发故障预测方法进行了研究。由于故障数据的分布参数为一常数，不随时间变化，因此通过统计推断确定故障数据的分布规律后，即可基于故障数据分布函数建立电子设备突发故障预测模型，对设备未来一段时间内的突发故障概率进行预测，并进行实例分析，验证了突发故障预测模型的合理性。

［1］马硕，焦现炜，田柯文，等.故障预测技术发展与分类［J］.四川兵工学报，2012，34（2）：93－95.

［2］刘爱军，金国庆.电子装备故障预测方法研究［J］.舰船电子工程，2012，32（12）：110－111.

［3］李斌，胡雷刚，肖明清.航空电子设备故障预测框架与方法［J］.空军工程大学学报（自然科学版），2011，12（2）：6－7.

［4］许丽佳.电子系统的故障预测与健康管理技术研究［D］.成都：电子科技大学，2009：5－9.

［5］孙旭.故障预测和健康管理（PHM）系统［J］.舰船科学技术，2011，33（9）：133－135.

［6］刘志花.无人机故障预测与健康管理技术研究［D］.北京：北京化工大学，2010：4－5.

［7］王昊天，石健.基于可用度模型的故障预测与健康管理方法［J］.系统工程与电子技术，2010，32（12）：2584－2589.

［8］杨媛媛.电力电子电路参数辨识与故障预测方法研究［D］.南京：南京航空航天大学，2011：58－82.

［9］吴翊，李永乐，胡庆军.应用数理统计［M］.长沙：国防科技大学出版社，2008：33－115.

［10］冯静，孙权，罗鹏程，等.装备可靠性与综合保障［M］.长沙：国防科技大学出版社，2008：200－201.