基于层次熵分析法的舰载雷达抗干扰效能评估❋

郭万海 邵晓方 滕 俊

（1.海军大连舰艇学院信息作战系 大连 116018）（2.海司军训部 北京 100036）

1 引言

无论是从各国军事训练的重点方向上，还是从近几年来几次局部战争中，都可以清楚地看到，在现代信息化战争条件下，舰载雷达都工作在复杂的电磁环境中，这就要求舰载雷达必须具有在复杂干扰条件下正常工作的能力。所以，对在干扰条件下的舰载雷达效能进行评估就显得非常重要。目前，国内外雷达界在雷达抗干扰性能评估方面做了许多分析研究工作，提出了一些评估方法。但是，对舰载雷达抗干扰效能度量尚没有一种较客观准确的方法。

本文介绍基于熵权的多级模糊综合评价对干扰条件下舰载雷达效能进行综合评估，用模糊数学的理论与方法将一些边界不清、不易定量的因素定量化，从而实现综合评价［1］。通常采用主观赋权法对指标进行评价，由于专家的知识、经验及其偏好等一些主观因素的存在，使确定出的权重系数真实性降低。为了尽量避免在确定权重系数时受人为的干扰，因此将层次分析法与决策中的熵技术结合，建立层次熵评价决策模型［2］，用于舰载雷达效能评价。

2 结合熵技术的模糊层次分析法

由于舰载雷达抗干扰系统指标的相对性、模糊性，因此采用模糊数学的理论与方法对舰载雷达系统抗干扰效能进行评估，模糊数学可有效地解决舰载雷达抗干扰系统中定性信息的处理。雷达抗干扰系统是一个复杂的系统，所以要用层次分析法（AHP）将复杂问题分解为若干层次和若干指标［3］。先用模糊数学的方法对各指标进行模糊化处理，再用AHP方法计算各指标对最终评估值的相对权重，再通过熵技术进行权重的修正，此种方法称之为结合熵技术的模糊权重分析法。

3 舰载雷达抗干扰效能模型

舰载雷达抗干扰效能主要由三个指标来衡量。它们是雷达信号、雷达固有抗干扰性能、雷达抗干扰技术［2］，为了计算方便，分别用 X1，X2，X3来表示。这三个指标又与许多因素有关，具体如下［3］：

1）X1：信号时宽X11，信号频宽X12，信号内部结构X13。

2）X2：雷达体制X21，雷达平均功率X22，雷达天线增益X23。

3）X3：频域抗干扰技术X31，天线副瓣增益X32，极化措施X33，抗干扰电路X34，脉冲重复频率X35。

根据以上指标，可建立舰载雷达抗干扰效能多级评估模型［5］，如图1所示。

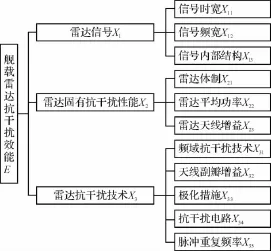
图1 多级评估模型

4 舰载雷达抗干扰效能指标体系及计算

4.1 指标因素分析及模糊化处理

考虑舰载雷达抗干扰系统特点和各因素的基本属性，本文选用逻辑推理法，根据相关分析和数据处理的结果确定各项因素的隶属函数。具体分析如下［6］：

1）X11为信号时宽，增大其值，相当于提高雷达输出信号的信干比，可以提高在频域上的抗干扰能力。它的模糊化处理采用如下隶属函数：

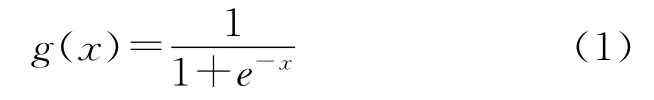
2）X12为信号频宽，增大信号的频宽将迫使敌方施放宽带干扰，干扰功率谱密度下降可提高雷达输出信干比，其隶属函数如下：

3）X13为信号复杂程度，信号内部结构越复杂，抗干扰能力就越强。该指标属于定性指标，无法用精确的数学公式描述。根据舰载雷达信号的特征，咨询专家意见，进行计分评估，其值在0～10之间，采用如下公式确定模糊隶属度：

4）X21为雷达体制，舰载雷达常用的雷达体制有脉冲压缩雷达、全相参雷达、相控阵雷达、多体制雷达等。根据它们抗干扰能力强弱，用模糊数学中二元对比排序法［7］计算指标的隶属度，计算过程如表1所示。

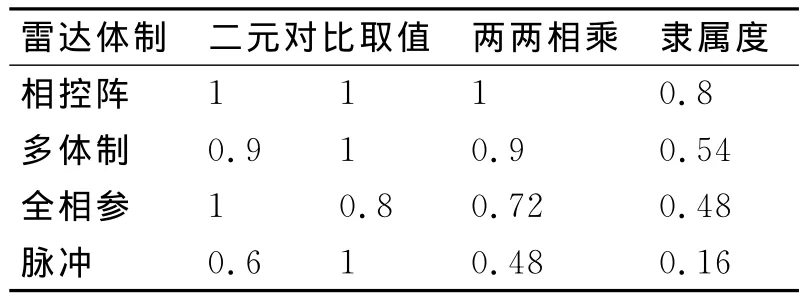
表1 雷达体制抗干扰性能隶属度

5）X22为雷达平均功率，雷达发射功率越大其抗干扰能力越强。舰载雷达发射功率范围在5kW～60kW之间，用模糊数学中的梯型隶属度函数对其进行模糊化处理，函数形式如下：

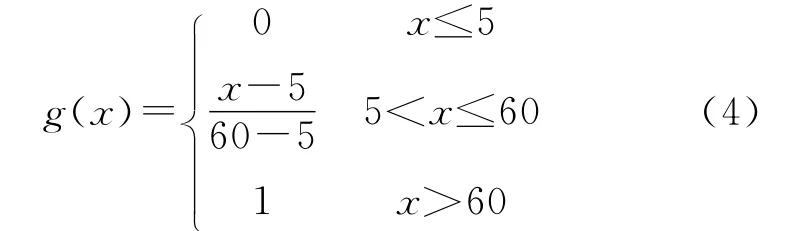
6）X23为雷达天线增益，增大天线增益可提高雷达抗干扰性能。舰载雷达天线增益一般为25dB～40dB之间，根据它的特点选用模糊数学中的S形隶属度函数对其进行模糊化处理，表达式如下：

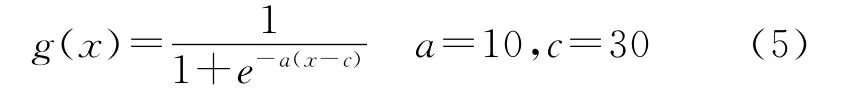
7）X31为频域抗干扰技术，X33为极化措施，X34为抗干扰电路，它们均为定性因素，其值的量化由经验值打分得出，其值在0～10之间，采用式（3）计算其隶属度。

8）X32为天线副瓣增益：副瓣增益越小抗干扰性能越好，故采用降半龄形分布函数确定隶属度，函数形式如式（6）所示：

9）X35为脉冲重复频率，根据脉冲重复频率个数来确定其性能优劣［5］，用式（7）确定脉冲重复频率跳动因子SJ，式（8）将该值归一化处理，确定隶属度，J为脉冲重复频率个数。

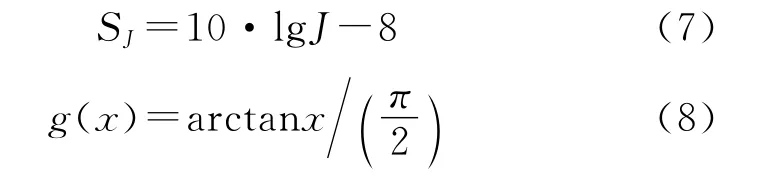
4.2 定量指标权重的确定

为了获取尽量准确的指标权重，本文研究采用层次分析法和熵技术相结合的方法确定指标的权重。所谓层次熵评估模型，是用层次分析法（AHP）决定指标的模糊权重，利用决策矩阵提供的信息，进一步用多目标决策中熵技术修正决策者先前决定的优先权重，以获得相对准确的指标权重［8］。由于层次分析法容易产生循环而不满足传递性公理，导致标度把握不准并丢失部分信息，解决这些问题的有效途径是使用熵技术对其进行修正。将层次分析法与熵技术结合用于干扰条件下舰载雷达效能的评价以往尚未涉及，本文拟在此方面进行探索。

4.2.1 构造判断矩阵

本文采用层次分析法（AHP）确定各评价指标对应于上一层某指标的相对重要性权值［6］。具体方法如下：

对同一层次的各元素关于上一层次中某一准则的重要性进行两两比较，构造判断矩阵A。A中元素aij表示i指标与j指标相对重要度之比，并有下述关系（即反对称矩阵）：

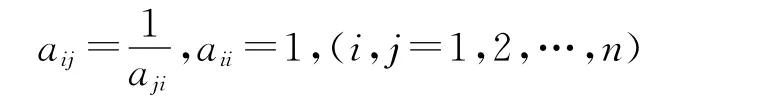
显然aij的比值越大，i相对j的重要度就越高，为了方便一般采用如表2所示尺度。

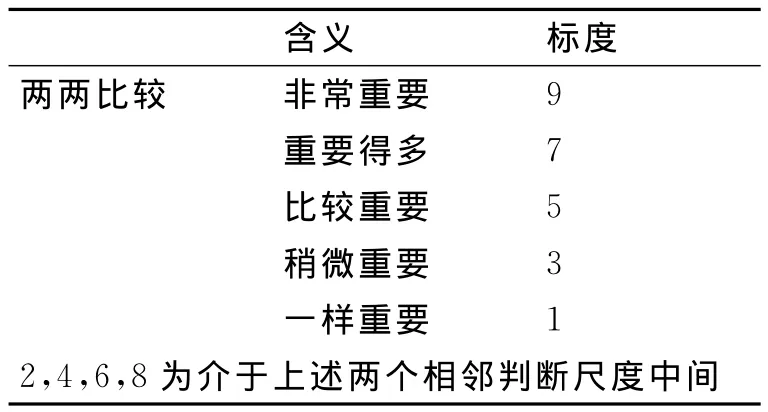
表2 判断尺度

4.2.2 计算权重向量，并进行一致性检验

用特征向量法中的和积法确定w：对矩阵A的各列向量进行归一化，得到标准矩阵B＝（bij）m×m，其中：

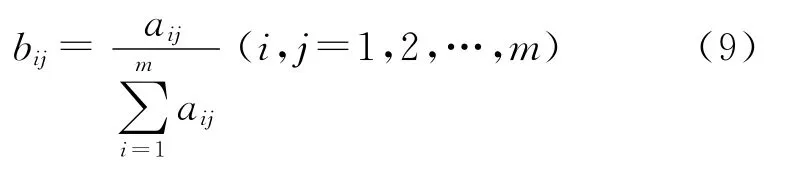
然后按行求和、归一化，所得列向量w＝（w1，w2，…，wm）T即为A 的特征向量，其中：

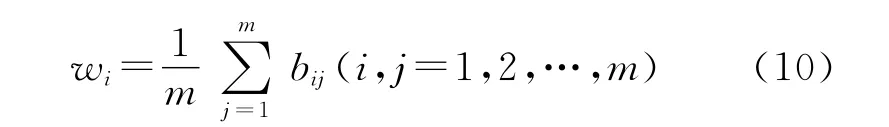
进一步计算矩阵A的最大特征根：

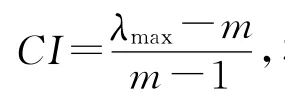
4.2.3 权重向量w的修正

通过熵技术对由层次分析法得到的权重向量进行修正。其具体步骤如下。

步骤1：根据标准矩阵B＝（bij）m×m，计算第j个指标xj的输出熵：

其中k＝（lnm）－1为常数；可证明：0≤E≤1；

步骤2：求指标xj的偏差度dj；

步骤3：计算指标xj的信息权重μj：

步骤4：利用信息权重μj修正由AHP法得到的权重向量w，得：

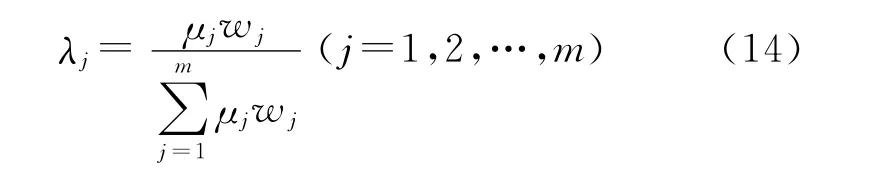
通过上述步骤得到各指标较为合理的权重向量λ＝（λ1，λ2，…，λm）T。

4.3 舰载雷达抗干扰性能计算

根据上述方法得到修正后指标权重，如表3所示。

舰载雷达抗干扰指标X1，X2，X3的隶属度可由下式计算［10］：

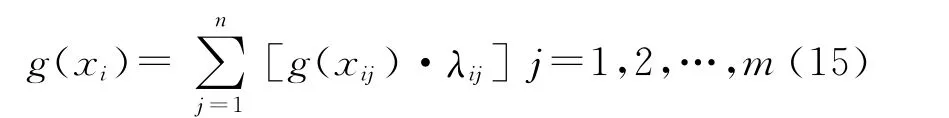
g（xij）为舰载雷达对于xij指标的隶属度，λij为指标xij的权值。舰载雷达抗干扰效能可由下式计算：

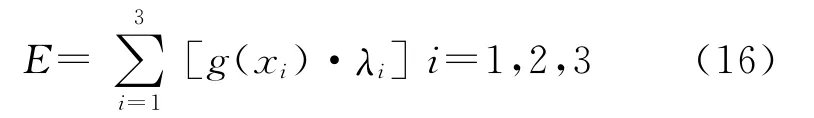
以美国海军两型雷达SPS－49、SPY－1为例，各性能指标的模糊隶属度如表4所示。

表3 修正后的指标权重

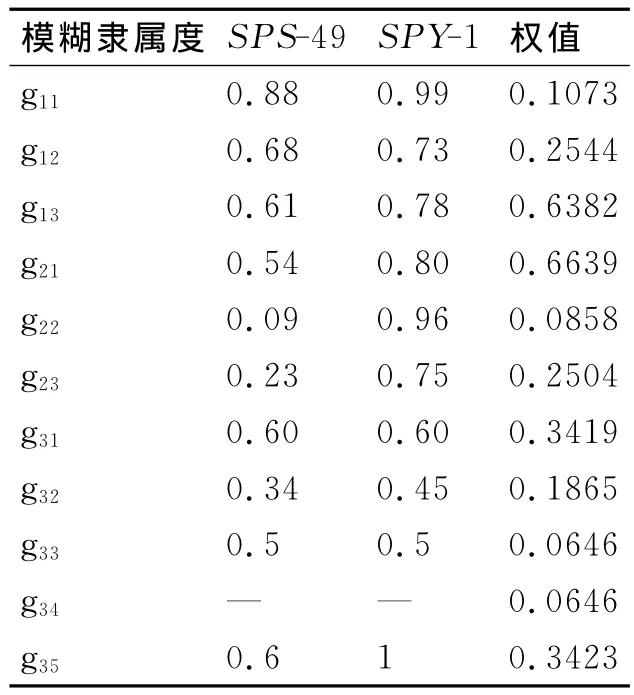
表4 性能指标模糊隶属度

分析这两种雷达的抗干扰效能，根据式（15）和式（16）计算得到，对于SPS－49，E1＝0.496；SPY－1，E2＝0.718。由这两个数据可以看出，SPS－49与SPY－1相比，后者的抗干扰性能占决定优势。

5 结语

本文分析了影响舰载雷达抗干扰性能的指标，利用了模糊数学的方法确定各因素的隶属度，通过层次熵分析法对干扰条件下舰载雷达综合效能进行了评价研究，从而将定性的评价结果转为定量的评价，尽可能地避免了评价中的人为因素，有利于考虑评估过程中的各种不确定性因素和定性因素，为较准确地评估整个雷达系统效能提供了一种新的方法，对整个舰载雷达作战效能分析具有一定的意义。

［1］徐昌文.模糊数学在船舶工程中的应用［M］.北京：国防工业出版社，1992：50－56.

［2］姜晔，储志宇.层次熵评价决策模型在航道网规划综合评价方面的应用［J］.水运工程，2001，32（6）：30－34.

［3］中航雷达与电子设备研究院.雷达系统［M］.北京：国防工业出版社，2005：112－128.

［4］王丕宏，张红.作战效能分析研究［J］.电光与控制，1995，2（4）：15－20.

［5］杨华冰，何清华，李执力.火控系统作战可用度研究［J］.火控雷达技术，2005（3）：32－35.

［6］郭晋媛，黄俊.模糊层次法评估机载雷达抗干扰效能［J］.电光与控制，2007，14（4）：151－153.

［7］胡永宏，贺思群.综合评价方法［M］.北京：科学出版社，2000：208－214.

［8］巫银花，陆勤夫，陈勇，等.干扰条件下舰载雷达效能评价研究［J］.舰船科学技术，2008，30（4）：85－88.

［9］张巨泉，李潮，黄洪旭.航空武器仿真中雷达干扰效果评估模块［J］.现代雷达，2004（4）：1－4.

［10］刘永红.电子对抗系统作战效能模型及其应用［J］.电子对抗技术，2005（5）：30－34.