基于飞行轨迹的捷联惯导系统算法仿真＊

石钊铭 王文革

（海装重庆局 重庆 401100）

1 引言

随着科学技术的进步，惯性导航技术朝着高精度、高可靠性、低成本、小型化的方向不断发展。由于捷联式惯性导航系统［1～4］是将惯性组件（陀螺仪和加速度计）直接固连到载体上，无需另外的固定平台，而是通过导航计算机来实现对载体的精确导航定位，与平台式惯性导航系统相比，具有可靠性好、体积小、重量轻和成本低等优点。虽然捷联式惯性导航系统在精度上稍逊于平台式惯性导航系统，但是通过进行一定的处理，已经可以满足舰船、飞机等载体的导航定位要求。

本文根据载体在空间中的运动特点，利用工程软件Matlab对基于飞行轨迹的捷联惯导系统算法进行了仿真。先是通过建立载体运动模型模拟出载体的运动轨迹，然后进行逆运算计算出陀螺仪和加速度计的模拟输出量（角速度和比力），并加入模拟噪声，最后通过合理的力学编排计算出载体的位置和速度信息；仿真试验证明，整个捷联惯导系统算法仿真是可行的。

2 载体飞行轨迹建模

为了验证仿真的正确性，需要比对捷联惯导算法求出的仿真运动轨迹和事先模拟的载体运动轨迹，通过分析载体每一时刻的导航定位误差来判断。为此需要建立载体的运动轨迹模型，利用计算机仿真载体的运动轨迹［5～8］。

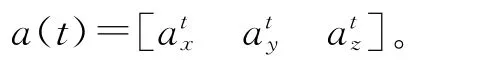
1）静止：载体的姿态角和加速度均为0，即：

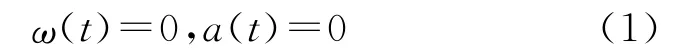
2）匀速直线运动：载体的姿态角为常数并保持恒定，加速度为0，即：

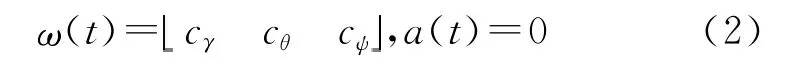
3）匀加速运动：载体的姿态角和航向角均为常数并保持恒定，即：

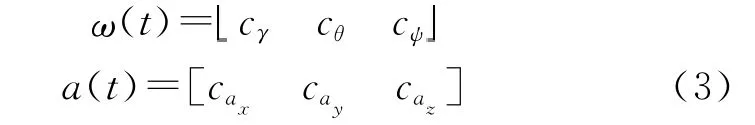
4）转弯运动：假设载体转弯过程没有发生侧滑现象，只在水平面内转弯。

设转弯过程中载体的运动速度为v，转弯半径为r，转弯角速度为ῶ，转弯时的向心力A完全由重力分量作用，横滚角的改变量为θΔ，则有：

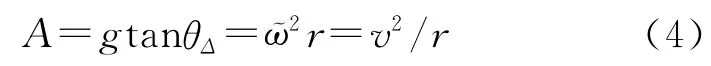
在这里，将转弯过程按照进入转弯阶段、转弯阶段和改平阶段分别进行分析。

（1）进入转弯阶段：

在该阶段，载体以保持角速度¯γ来改变横滚角，加速度不变。设该阶段的初始时刻为t0，则有

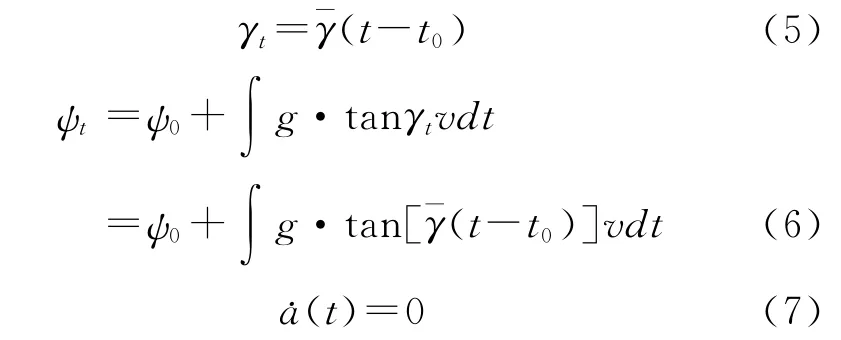
（2）转弯阶段：

在该阶段，载体保持横滚角和加速度不变，角速度为ω0。则有

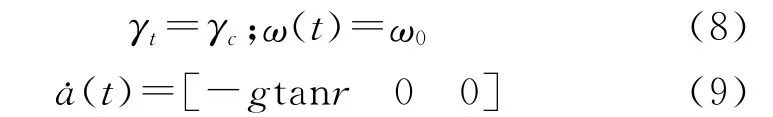
（3）改平阶段：

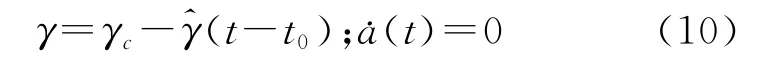
5）爬升或下降运动：由于下降过程刚好与爬升相反，这里只分析载体的爬升运动。假设沿运动轨迹前进的方向载体运动速度保持不变，并将载体的爬升过程分为拉起阶段、爬升阶段和改平阶段等三个过程进行分析。

（1）拉起阶段：

设半径为r，载体的俯仰角保持角速度¯θ逐渐增大，则有：

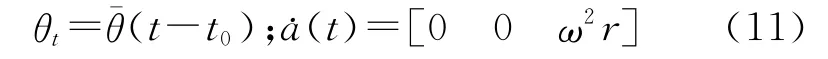
（2）爬升阶段：

在达到要求高度时，载体的俯仰角保持恒定，加速度也保持不变，即：

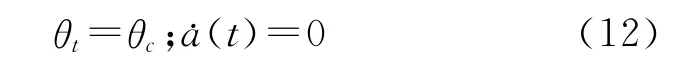
（3）改平阶段：

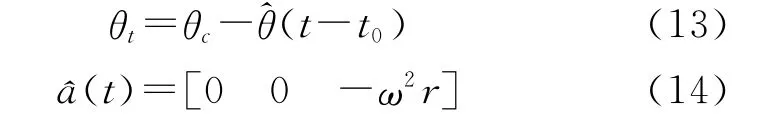
3 惯性器件数学模型

3.1 陀螺仪仿真模型

陀螺仪［9］是测量载体运动角速率的部件，其输出为

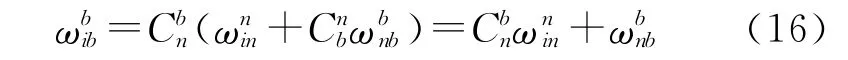
陀螺仪的测量误差ε包括常值漂移误差εb、一阶马尔科夫过程随机误差εr和测量白噪声ωg，即：

式中：

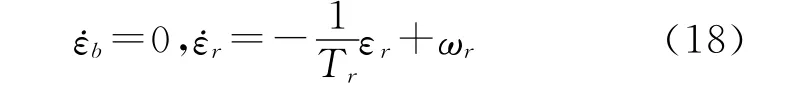
式（18）中，Tr为相关时间，ωr为白噪声。

3.2 加速度计仿真模型

加速度计［9～10］是测量载体在运动过程中的轴向比力的部件，其输出为

式（19）中，fb为加速度计测量的比力为测量误差。

从比力方程可知：

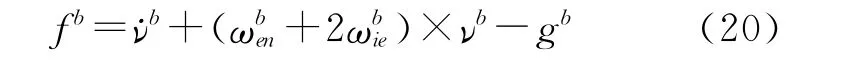
假设加速度计的测量误差是一阶马尔科夫过程，即：

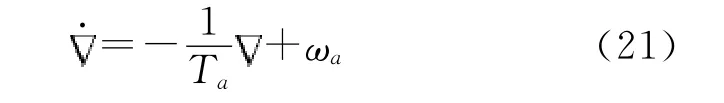
式（21）中，Ta为马尔科夫的相关时间，ωa为测量白噪声。

4 捷联惯导算法仿真力学编排

具体步骤如下：

1）初始对准：给仿真系统设定初始输入量（包括初始速度和位置）；

2）载体运动轨迹模拟，并计算陀螺仪和加速度计的模拟输出量；

3）求解四元数微分方程：

通过毕卡逼近法求得该方程的解为

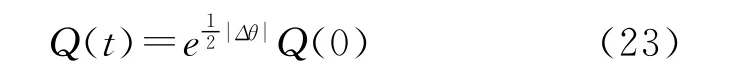
4）四元数最佳归一化处理：

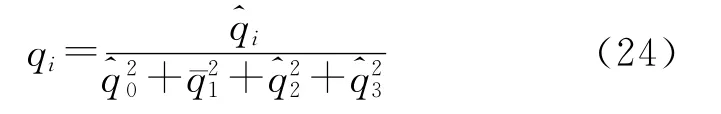
5）计算姿态矩阵：

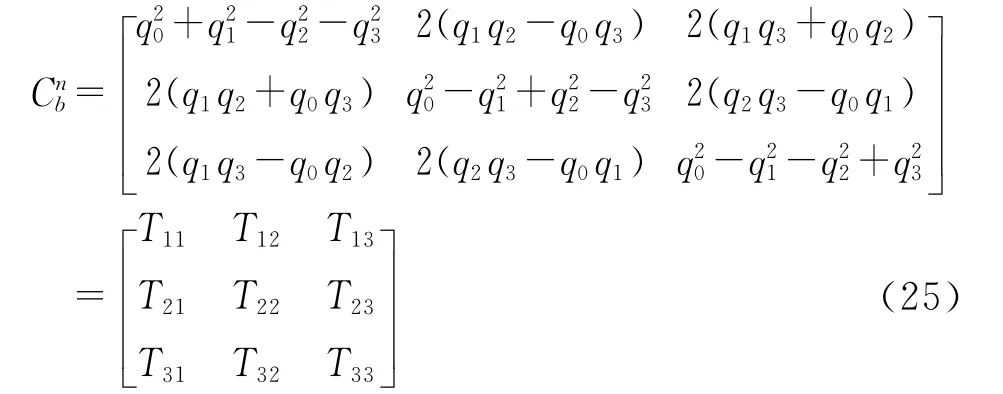
6）提取姿态角：

俯仰角：

横滚角：

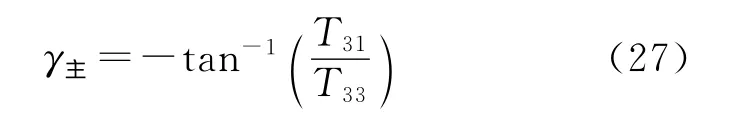
偏航角：

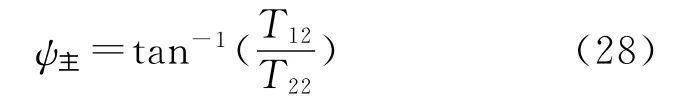
7）比力坐标变换：将比力信息从载体坐标系投影到导航坐标系：

8）运动速度的计算：

惯性导航的基本方程为

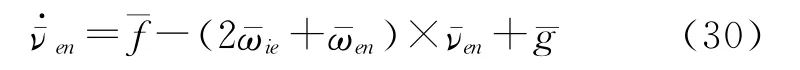
9）姿态角速率计算：

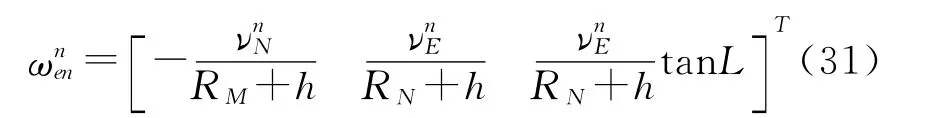
10）地理位置计算：

纬度：

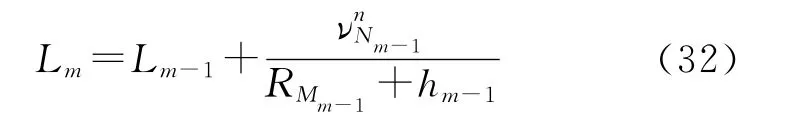
经度：

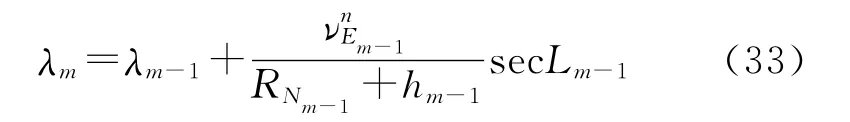
高度：

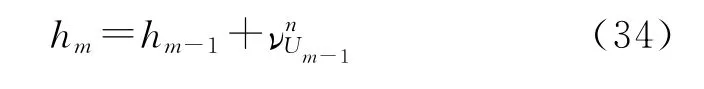
5 仿真试验与分析

为了验证仿真系统的有效性，采用四元数法进行导航计算，设计如图1所示的载体飞行轨迹（从图可知，载体的运动轨迹组合了匀加速，转弯、爬升和下降等状态）。并设定初始参数如表1所示。

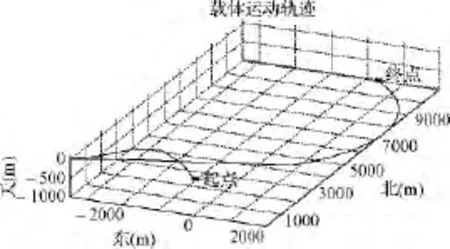
图1 载体飞行轨迹仿真

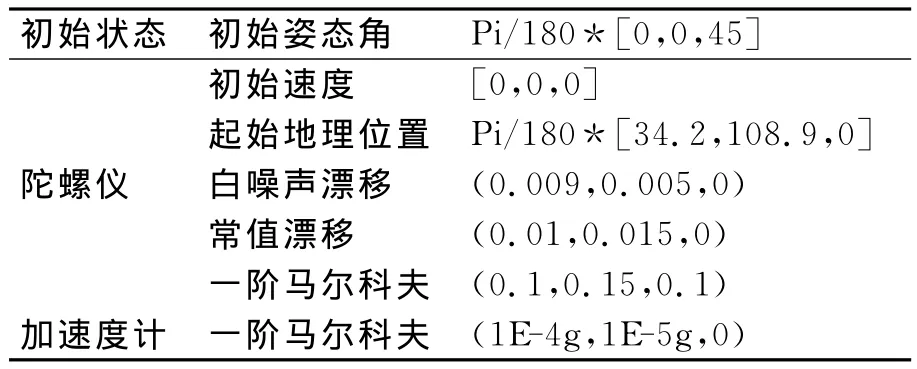
表1 初始参数表

图2为INS仿真的载体飞行轨迹，图3、图4为通过仿真计算求出的载体运动实时的速度误差、位置误差。从图2～图4可知，仿真开始一段时间，载体速度误差和位置误差均偏小，接近于0，随着时间推移，两误差逐渐累积。

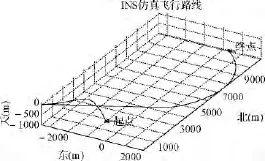
图2 INS仿真飞行轨迹

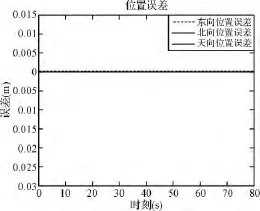
图3 位置误差

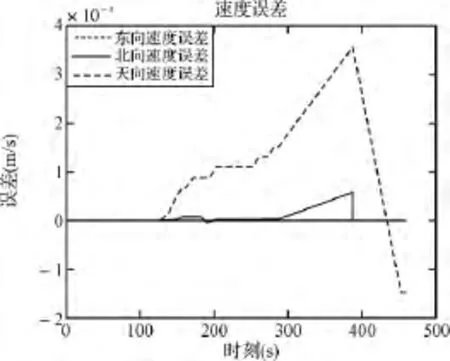
图4 速度误差

6 结语

现代信息化战争对导航的要求越来越高，惯性导航系统由于完全依靠自身设备完成导航定位，既不要求外部信息，也不向外界发送信息，具有隐蔽性好、工作全天候等优点，近年来越来越受各国的重视，尤其是捷联式惯导系统。本文根据捷联式惯导系统的基本原理，利用计算机仿真技术设计了捷联惯导算法仿真系统，仿真结果验证了算法的正确性和系统的可行性，为今后捷联系统的实物设计和开发奠定了基础。

［1］Lee J.G.，Yoon Y.L.，Mark J.G.，et al.Extension of Strapdown Attitude Algorithm for High－Frequency Base Motion［J］.AIAA Journal of Guidance of Control and Dynamics，1999，13（4）：738－743.

［2］李路苹，徐景硕，陈震.基于VS的捷联惯导系统仿真器设计［J］.计算机仿真，2013，30（6）：94－98.

［3］戴邵武，马长里，代海霞.北斗双星／SINS组合导航中的捷联惯导算法研究［J］.计算机与数字工程，2010，38（2）：1－4.

［4］陈银溢，郭圣权，岳凤英.微惯性测量组合算法的优化［J］.科技情报开发与经济，2004，14（8）：176－177.

［5］段小庆，王宏力，郑佳华.高动态下捷联惯导系统姿态算法比较研究［C］／／2007系统仿真技术及其应用学术会议论文集，2007：75－77.

［6］查峰，许江宁，覃方君.旋转捷联惯导系统的轨迹仿真算法［J］.系统仿真学报，2013，25（3）：499－503.

［7］胡鑫，韩崇伟，王玮，等.基于Simulink与 M语言的捷联惯导系统仿真方法研究［J］.科学技术与工程，2010，10（16）：4032－4036.

［8］刘放，陈明，高丽.捷联惯导系统软件测试中的仿真飞行轨迹设计及应用［J］.测控技术，2003（5）：24－29.

［9］蒋黎星.捷联惯性导航算法及半实物仿真系统研究［D］.南京：南京理工大学，2007.

［10］曹岩，赵家胜，王伟，等.弹载捷联惯性导航系统算法及仿真［J］.西安工业大学学报，2011，31（3）：232－235.