航运事故致因机理突变模型的构造与应用

陈蜀喆， 黄立文

(1. 内河航运技术湖北省重点实验室， 武汉 430063； 2. 武汉理工大学 航运学院， 武汉 430063)

航运事故致因机理突变模型的构造与应用

陈蜀喆1,2， 黄立文1,2

(1. 内河航运技术湖北省重点实验室， 武汉 430063； 2. 武汉理工大学 航运学院， 武汉 430063)

利用突变理论对航运事故发生机理进行定量研究。由于该研究是一项系统工程，涉及到控制变量的提取和量化、突变模型和固有特征量的构造以及最终分析等一系列复杂过程，因此基于现有学者在突变模型应用于航运事故发生机理方面的研究，对突变模型的构造和应用过程中存在的具体问题进行深入研究，设计从控制变量提取量化、突变模型构造及拓扑到最终机理分析的整套框架。在取得足够的事故样本后，可利用该框架进一步明确航运事故机理，最终实现事故风险预控。

水路运输； 航运事故； 机理； 突变模型； 构造； 应用

1 航运事故致因机理概述

除搁浅、风灾、浪损等事故类型对通航环境相对敏感，自沉等事故类型对船舶状态相对敏感外,航运事故发生多是复杂因素相互接触、相互作用的结果。从安全角度分析，船舶作为水上运输的载体，其运行过程处于随时间和空间不断变化的连续过程之中。而由人-船-环境形成的安全系统受通航影响因素的扰动，会使船舶安全稳定状态发生变化，如果因素的变化超过了一定的限度，船舶会由一种稳定状态变化到另一种稳定状态，此过程往往代表着航运事故的发生。

2 突变理论模型在航运安全系统中的应用

2.1突变理论

突变理论[1](Catastrophe Theory)用来研究动态系统在连续发展过程中出现的突变现象，解释突然变化与连续变化因素之间的关系。其聚焦在如何描述动态系统在连续发展过程中的突变现象，认为描述动态系统的势函数具有表征系统某种倾向的能力，可描述为

V=V(x，c)

(1)

式(1)中：x为系统状态变量(系统输出变量)；c为系统控制变量(系统外部输入变量)。

2.2系统函数突变形式

系统中，如果控制参数中的元素不超过4个，则系统势函数最多有7种突变形式(见表1)。

表1 基本突变模型

2.3尖点突变函数在航运安全系统中的应用

多数学者认为影响航运安全状态变化的控制变量总体可简化为人的因素和物的因素。[2]选取适合以航运事故系统的二维控制变量(人的因素和物的因素)及一维状态变量(航运系统安全状态)来共同反映航运安全系统势能的尖点突变模型描述事故可能机理较合理。[3]然而，该研究目前基本上还处于理论阶段，仅针对突变模型的特征描述事故的可能机理，并没有提出实际事故机理的量化计算模型。

由于航运安全系统的特殊性，系统的安全状态、人的不安全行为和物的不安全状态均存在与实际相对应的临界平衡点。因此在实际应用中，需对尖点模型(见图1)的一般势函数进行完善。

V(x)=(x-x0)4+(u-u0)(x-x0)2+

(v-v0)(x-x0)

(2)

式(2)中：x为航运系统安全状态；u为人的因素；v为物的因素；x0，u0，v0为系统固有的特征量，分别表示系统安全状态、人为因素和物的因素对应的临界平衡点。此时平衡曲面方程为

4(x-x0)3+2(u-u0)(x-x0)+(v-v0) =0

(3)

令V的Hessen矩阵为0，求出奇点集

12(x-x0)2+2(u-u0) =0

(4)

联立式(3)和式(4)，得到分叉集

8(u-u0)3+27(v-v0)2=0

(5)

求出分叉集后，利用系统平衡面和分叉集绘制出来的尖点突变模型解释航运事故的产生机理。采用该方式对航运事故机理进行解释具有一定的直观性，可解释航运事故的形成机理，但在具体模型构造过程中有以下问题有待解决：

1) 航运安全系统各关键因素的提取和量化。

2) 航运事故的发生在某种程度上可看作是人的因素和物的因素相互接触、相互作用的结果，实际操作过程中应注意如何通过船舶和环境因素的合并构造突变模型中物的因素。

3) 虽然燕尾突变模型在机理分析时较为复杂，但仍可尝试将人-船-环境系统中具有的三维控制变量作为输入进行机理分析。

4) 系统固有的特征量的确定。

5) 突变模型的具体构造方法。

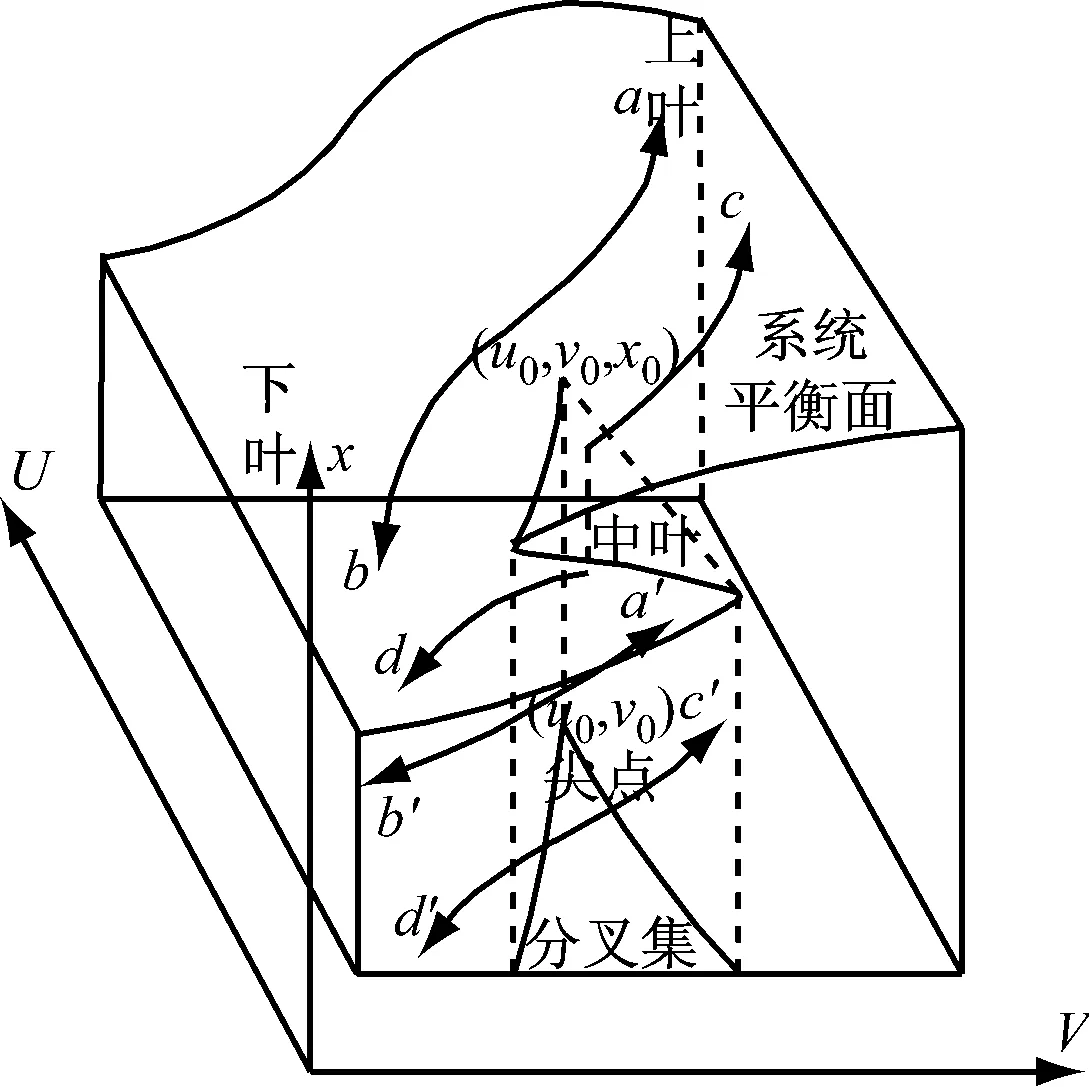
注：(1)上叶为要素之间和谐有序的安全状态；下叶为航运中断的灾害状态。

(2)a′-b′曲线变化过程与分叉集无交点，平稳渐变；c′-d′曲线穿过褶皱曲面从上叶突跳到下叶，系统不稳定发生突变。

图1 航运事故尖点突变模型

3 突变理论模型构造

3.1航运安全系统各关键因素的提取和量化

3.1.1因素提取

在提取航运安全系统中的关键因素时，以事故案例为基础，使用情景分析法，从更深层次挖掘分析事故的发展变化机制。

在实际分析过程中，该流程可简化为4部分(见图2)。

(1) 事故描述及节点划分：对案例中的事故船按时间序列和空间相对位置序列进行描述；

(2) 初步确定情景空间：根据情景准备阶段的事故描述,对事故节点进行划分；

图2 航运事故情景案例分析流程

(3) 关键因素提取及情景确认：对于划分的情景空间，针对其各阶段的特点动态提取关键因素;

(4) 情景发展路径分析：对事故情景的概率、风险进行决策和预测。

对于实际情景分析，关键因素与人-船-环境安全系统随时空变换的途径密切相关，在不同的事故发展阶段，其会随时增减。此外，某些能直接切断事故链的主线因素还会利用数值方法加强其效果。现阶段，实际能提取的关键因素主要存在于通航环境方面，对于船舶和人为的关键因素而言，一般根据船舶主机、辅机和通信设备的失误率以及人的多次行为随不同状态的失误率来模糊确定。

3.1.2因素量化

目前，因素量化仍是困扰研究人员定量描述航运安全的瓶颈。因素量化即对随时空变化的通航安全影响因素进行表述，使其能够反映出当前单一因素或多因素的耦合作用对系统可能发生安全事故的影响程度。因素量化的一般流程见图3。

图3 因素量化流程

量化模型以各因素对航运事故发生的影响概率为基础，是该因素(某种程度)在某时间区间内某种事故统计中的发生次数n与该因素在事故报告统计期间内的发生次数N的比值，即

Pi=n/N

(6)

在此基础上，可对量化模型进行改进，主要利用船舶尺寸加权系数对发生概率进行修正，采用灰色关联分析法对因素相互影响进行分析、对发生概率进行修正。若航运事故样本数较少，可通过数据拟合的方式对量化模型小样本进行适当扩充，在反映现有海事事故报告统计情况的基础上，增加海事管理部门和船舶驾驶人员等的主观评判，并对量化后的数据进行融合。

3.2利用突变级数法构造控制变量

突变级数法以突变理论为基础，是一种对评价目标进行多层次矛盾分解，然后将突变理论与模糊数学相结合产生突变模糊隶属函数，再由归一公式进行综合量化运算，最后归一为一个参数，从而对评价目标进行排序分析的一种综合评价方法。利用该方法求解分叉集之后，可建立归一公式，主要利用一维状态变量的突变模型，具体内容见表2。

表2 一维状态变量的突变级数法参数求解

根据突变级数法，可将人-船-环境系统中各子因素对航运安全事故的影响程度进行综合量化运算，即得到控制变量。因此，实际控制变量即为人-船-环境系统中各子因素的集中和浓缩。对于以人的因素和物的因素为控制变量的尖点模型，还需将船舶因素和环境因素进行二次综合量化运算，归一为物的因素后作为控制变量输入。[4]

3.3系统固有特征量构造

系统固有特征量可理解为控制变量和状态变量对应的临界平衡点。从某种意义上讲，其只是将原有尖点模型中控制变量和状态变量均为“0”的临界平衡状态进行某种意义上的平移，以达到表述实际航运事故中人、物因素与航运系统安全状态的一种平衡关系。引入系统固有特征量后，对式(5)而言，构造控制变量时就不需要按照原有分叉集8u3+27v2=0中u≤0来构造，只需满足u≤u0即可。在实际构造中，一般以尖点模型的“尖点”作为系统固有特征量(即图1中分叉集的尖锐点)。

对于系统固有特征量的构造，应根据实际事故类型、事故时空特征等具体情况进行区分。得到因素量化数值后，可采用突变级数法对这些因素量化数值按人和物进行归类。一般的流程见图4。

图4 因素固有特征量构造流程

3.4突变理论模型的构造

基于航运安全系统的突变理论模型的构造涉及到具体的量化计算过程，相对于现有的理论框架，应具有更加细致的可操作性。[5-6]其构造流程见图5。

图5 航运安全系统的突变模型构造流程

建模过程一般可采用尖点突变模型或燕尾突变模型。[7]

3.4.1尖点突变模型

势函数参见式(2)；平衡曲面方程参见式(3)；奇点集参见式(4)；分叉集参见式(5)。

拓扑：对于式(3)，令x′ =x-x0，u′=u-u0，v′=v-v0，等价为x′3+1/2u′x′+1/4v′ =0;令p=1/2u′，q=1/4v′,则平衡曲面方程为x′3+px′+q=0，可得

当(q/2)2+(p/3)3lt;0时，系统有3个实根，即系统有3个平衡位置，表示的区域称为不稳定区域，对应图1的中叶。

当(q/2)2+(p/3)3gt;0时，系统有1个实根，即系统有1个平衡位置，表示的区域称为稳定区域，此区域内的任一点仅有唯一的1个实数与之对应，对应图1的上叶和下叶。

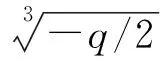
3.4.2燕尾突变模型

势函数：

V(x)=x5+ux3+vx2+wx

(10)

平衡曲面方程：

5x4+3ux2+2vx+w= 0

(11)

奇点集：

20x3+ 6ux+2v= 0

(12)

分叉集：联立式(11)和式(12)，消去x获得。

拓扑：对于燕尾突变模型而言，由于其控制变量较多，势函数及平衡曲面方程均较为复杂，在实际拓扑分析过程中应考虑通过限制某一控制变量来对其余控制变量进行分析。对于实际平衡曲面方程而言，可分别按照各控制变量=0来分析。

(1) 控制变量v= 0，即研究u-w截面的情况。

因此，可根据u-w的具体情况讨论平衡曲面、势函数与奇点稳定性的关系。

(2) 控制变量w= 0，即研究u-v截面的情况。

此时平衡曲面方程化简为5x4+3ux2+2vx= 0，可等价为x(5x3+3u2+2v)= 0，该式可转化为一元三次方程进行分析，具体过程可参照尖点突变模型。

(3) 控制变量u=0，即研究v-w截面的情况。

此时平衡曲面方程化简为5x4+2vx+w= 0，该式为一元四次方程，可结合费拉里公式和盛金公式加以求解和讨论。

基于以上分析，可对燕尾突变的控制参数特点, 势函数形式、平衡曲面方程和奇点稳定性关系有一定认识，可针对具体航运安全系统讨论1个状态变量、 3个控制变量的演变机理并分析其突变特点。

4 基于突变理论的航运事故致因机理分析

利用突变模型对航运事故的发生机理进行分析，其实质是对构造的突变模型的状态变量的多值性进行分析。无论是采用尖点突变还是燕尾突变，其实质都是分析控制变量参数在某个范围内变化时，安全状态函数值是否只有一个极值，若存在多个值与之对应，则系统必然处于不稳定状态。

航运事故可通过调节人-物控制变量进行预防。在可能的情况下，应尽可能避免落入分叉集范围内。

图6 控制变量与突变模型的关系

因此，实际模型与事故机理可由图7来描述。

图7 航运事故致因机理

5 结 语

目前对于航运事故机理的研究多是基于系统控制变量要素的静态和定性方面的分析，难以反映航运系统安全随控制变量变化而发生航运事故的突变过程[8]，对于事故发生控制变量也不能给出定量的描述，因此难以用来对实时情况进行预控。

构造航运事故发生机理突变模型是利用突变模型对航运事故发生机理进行分析的一种量化手段，可对控制变量变化对安全系统的影响进行定量分析[9]，是对航运事故分析的一种新的尝试[10]。在取得足够的事故样本之后，航运事故发生机理可在现有研究基础上进一步细化及量化，最终实现事故风险的预控。

[1] 勒内·托姆.突变论：思想和应用[M].周仲良,译．上海:上海译文出版社,1989．

[2] 郭君,刘清．基于突变理论的航运事故发生机理[J].水运管理,2008,30(4)：25-28.

[3] 林大建,蔡嗣经,周永安．基于蝴蝶型突变理论的安全生产保障系统分析和探讨[J].中国安全科学学报，2007,17(10):28-31.

[4] 刘文远.陶娟．基于突变理论的近海船舶航行安全评价[J].中国安全科学学报2010,20(10):113-118.

[5] 潘岳．突变理论在岩体系统动力失稳中的应用[M]. 北京:科学出版社,2008.

[6] YOU P, MOU R, ZHOU D. Analysis of Safety State of Dangerous Goods Transport System Based on Catastrophe Theory[C]. International Conference on Transportation Engineering, 2009.

[7] 沈斐敏. 交通事故致因分析的突变模型[J]. 福建工程学院学报,2006,4(6):751-754.

[8] 佘廉,王超．水运交通灾害预警管理[M].石家庄:河北科学技术出版社,2004.

[9] GONG Zhimin, ZHOU Xinquan, BO Zhai. The Application of Catastrophe Theory in the Safety Assessment of Construction[C]. 3rd International Symposium on Modern Mining and Safety Technology, 2008.

[10] SWARUP K S. Artificail Neural Network Using Pattern Recognition for Security Assessment and Analysis[J]. Neurocomping, 2008,71(4): 983-998.

ConstructionandApplicationofShippingAccidentCauseMechanismCatastropheTheoryModel

CHENShuzhe1,2，HUANGLiwen1,2

(1. Hubei Key Laboratory of Inland Shipping Technology, Wuhan 430063, China; 2. School of Navigation, Wuhan University of Technology, Wuhan 430063, China)

The mechanism of marine accidents is quantitatively studied by the catastrophe theory. The research involves a series of complex processes, such as identification and quantification of control variables, the construction and analysis of the catastrophe theory model and its inherent characteristic value. Certain achievements of the research in mechanism of marine accidents with the catastrophe theory have been made. Some specific problems in construction and application of the catastrophe theory model are focused on the basis of those achievements. The whole framework of process is designed from extraction of control variables and quantification, construction of the catastrophe theory model and its topology to the final mechanism analysis. The framework allows determination of the mechanism of marine accidents, hence, control of the risks, provided that enough data are collected.

waterway transportation; shipping accident； mechanism； catastrophe theory model； construction； application

2014-05-08

国家自然科学基金(51379170)；交通应用基础研究项目(2012-329-811-140)；中央高校基本科研业务费专项资金(2013-IV-005)

陈蜀喆 (1979—)，男，湖北武汉人，讲师，博士，主要从事交通信息工程及控制研究。E-mail:404816705@qq.com

1000-4653(2014)03-0036-05

U698.6

A