基于现场锤击试验的地铁轨道振动特性分析及参数研究

李克飞，韩志伟，刘维宁，孙京健

(1.北京市轨道交通建设管理有限公司，北京 100037;2.北京交通大学土木建筑工程学院，北京 100044)

城市轨道交通正处在一个高速发展期，快速发展的轨道交通网在方便市民出行的同时，也引发了一定的环境振动和噪声问题。随着北京地铁新线的陆续开通，部分减振轨道区段钢轨出现异常波磨，造成了日趋严重的噪声问题。列车运行下钢轨振动加速度及车内噪声对比测试结果表明:北京地铁减振轨道的异常波磨问题是由地铁轮轨共振造成的［1］。

轨道结构的动力特性分析是开展轮轨耦合振动研究的基础。对于轨道结构动力特性的研究，国内外学者已做了大量工作，文献［2］对轨道结构的竖向动力特性进行了分析，文献［3-4］对轨道结构的横向动力特性进行了研究。

地铁轨道结构的动力特性取决于各组成部分(钢轨、扣件系统、轨枕和道床等)的物理特性及其组合形式。根据频率范围不同，轨道结构动力响应可分为低频振动，中频振动和高频振动［5］，如表1所示。

表1 轨道结构动力响应分类［5］

轨道结构的动力特性可通过有限元法［4］、数值分析法［6］、解析法［7］和试验分析法［8-9］等方法获得。基于现场锤击试验的模态分析法操作简单，容易获得较大的激励力和较高阶的固有频率，是一种比较经济、理想的测试方法。

实测轨道结构具有真实的边界条件、材质和结构内阻，可获得比计算更接近实际的结果;然而其只能针对特定的轨道系统进行测试，较难对不同参数的影响情况进行针对性研究。

基于轨道结构周期性频域解析模型，结合北京地铁在线锤击试验，通过计算轨道结构在固定脉冲荷载下的频响函数，对0～2 000 Hz内轨道结构的动力响应主频进行分析;并通过改变轨道结构参数，分别研究了轨下支撑刚度、阻尼，枕下支撑刚度、阻尼和轨枕支撑间距等对各轨道动力响应主频的影响情况，从而为避开地铁轮轨共振提供一定的理论基础。

1 现场锤击试验

为获得减振器轨道的竖向动力特性，对地铁Ⅲ型减振器扣件轨道(图1)开展在线锤击试验。

图1 Ⅲ型减振器扣件

选取轨道结构上6.25 m的测试范围，其间包含11组扣件，相邻扣件间距为0.625 m，如图2、图3所示。测试中选取21个锤击点和4个测点，均分别位于扣件正上方及相邻扣件的跨中正上方，其中偶数编号点位于相邻扣件中间，奇数编号点位于扣件正上方。

为了避免测试中的误差及随机干扰，对至少6组效果较好的数据进行处理，图4、图5分别为锤击力典型时程与频谱和钢轨振动加速度典型时程与频谱。

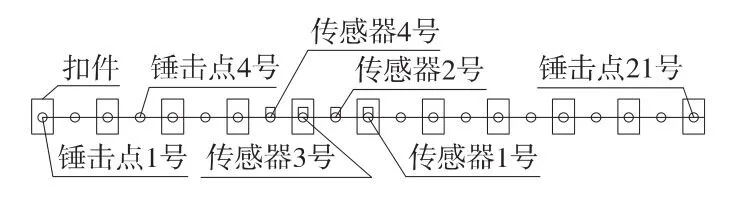
图2 锤击点及测点布置

图3 锤击试验现场照片

图4 锤击力典型时程和频谱

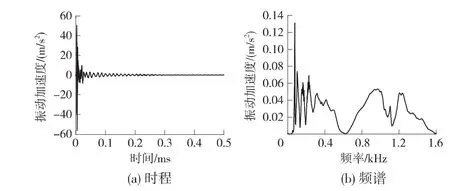
图5 钢轨测点振动加速度典型时程和频谱

为保证数据的可靠性，对测试数据均进行相干函数分析，试验中数据相关系数均大于0.8，图6为典型相干函数曲线。

图6 典型相干函数曲线

利用试验得到的锤击力和振动加速度数据，获得Ⅲ型减振器轨道的振动加速度频响函数，如图7所示。

图7 Ⅲ型减振器扣件轨道频响函数

结合文献［5］中对各轨道结构动力响应主频的定义，可以看出:Ⅲ型减振器扣件轨道的系统振动频率ft在80 Hz左右，钢轨共振频率fr和反共振频率fb－a在200～300 Hz范围内，pinned-pinned共振频率 fpp在1 000 Hz左右。

现场锤击试验相对较为方便、理想，却只能针对特定的轨道结构进行试验，较难对不同轨道结构参数的影响情况进行针对性研究。

2 轨道结构动力响应主频分析

基于轨道结构周期性频域解析模型，结合以上锤击试验结果，通过计算轨道结构的振动频响函数，在0～2 000 Hz范围内，对轨道结构的各振动响应主频进行分析;并通过改变轨道结构参数，分别研究轨下支撑刚度、阻尼，枕下支撑刚度、阻尼和轨枕支撑间距等对各轨道动力响应主频的影响情况。

2.1 轨道结构的周期性频域解析解

采用经典的双层离散支撑轨道模型，将钢轨下部结构模拟为双层离散质量－弹簧－阻尼体系，如图8所示。相邻离散支撑间距为Lcell，将双层支撑单元刚度通过复合刚度来表示，转化为图9所示的单层轨道模型，激振点y和响应点ξ如图9所示。

图8 双层离散支撑轨道模型

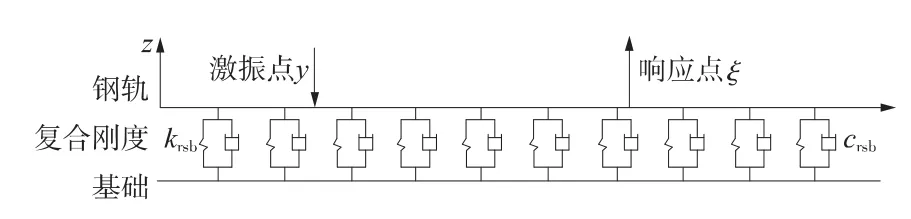
图9 复合刚度下轨道模型

轨下双层支撑单元的复合刚度为ckrsb

其中，ckr为轨下支撑的复合刚度，ckr=kr+icrω，kr为轨下支撑刚度;cr为轨下支撑阻尼;cksb为枕下支撑的复合刚度;cksb=ksb+icsbω，ksb为枕下支撑刚度;csb为枕下支撑阻尼;i是虚数单位，ω为角频率，Ms为等效参振质量，综合考虑了轨枕和道床的参振效应［10］。

建立轨道基本支撑单元Lcell内的局部坐标系～，如图10所示。激振点y在单元局部坐标内的投影为:fb－a。响应点ξ的坐标为ξy，其在单元局部坐标系内的投影=ξy－nξyLcell，ny，nξy分别为激振点 y 和响应点 ξ距整体坐标原点长度中所含有的基本单元Lcell的个数。

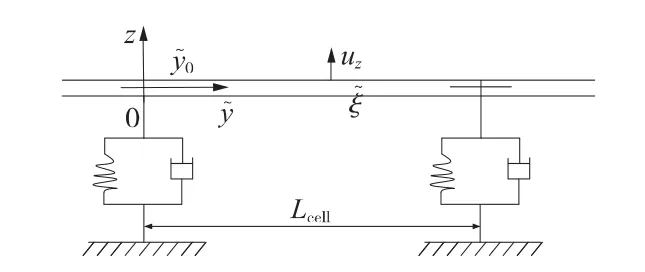
图10 单元局部坐标系

单位脉冲荷载作用在点y时，在ξ点所产生的频响函数F(ξ，ω)，可以通过轨道上两点间的传递函数i(y，ξ，ω)取得［10，11］

根据(2)式可以看出，在轨道结构上观察点ξ与激振点 y 间的频响函数zi+(nξy－ny)Lcell，ω)，采用传递矩阵法［10］，可以表示为激振点y的状态向量S，ω)和(nξy－ny)+1 个单元的传递矩阵的乘积。轨枕支撑单元的传递矩阵Ttrack(Lcell，ω)和激振点y的状态向量 S，ω)见已有研究成果［7，10，11］。

2.2 轨道解析模型验证

利用以上轨道解析模型对Ⅲ型减振器扣件轨道的频响函数进行求解，模拟结果与锤击测试结果进行对比，如图11所示。

图11 轨道结构频响函数测试与模拟结果对比

轨道结构中钢轨采用60 kg/m轨，单位长度质量mr=60 kg/m，弹性模量E=210 GPa，横截面面积A=7.60×10－3m2，截面惯性矩 I=3.04×10－5m4，结构阻尼比 ξr=0.01。

对于离散支撑轨道模型，轨枕单位长度质量ms=50 kg，支撑间距 Lcell=0.625 m，参振质量 Ms=260 kg/m。轨下支撑采用Ⅲ型减振器的刚度及阻尼为:kr=10 MN/m，cr=0.05 MN·s/m;枕下支承的刚度及阻尼为:ksb=100 MN/m，csb=0.05 MN·s/m。

根据图11的对比结果，可以看出:Ⅲ型减振器轨道频响函数的模拟结果和测试结果吻合较好，验证了轨道结构周期性频域解析模型的正确性，证明了该模型可用于研究轨道结构动力特性及其参数优化问题。

2.3 轨道结构参数研究

为了研究不同轨道结构参数对轨道动力特性的影响情况，在保持其他参数不变的情况下，对轨道结构参数进行调整，如表2所示，并将计算结果进行对比。

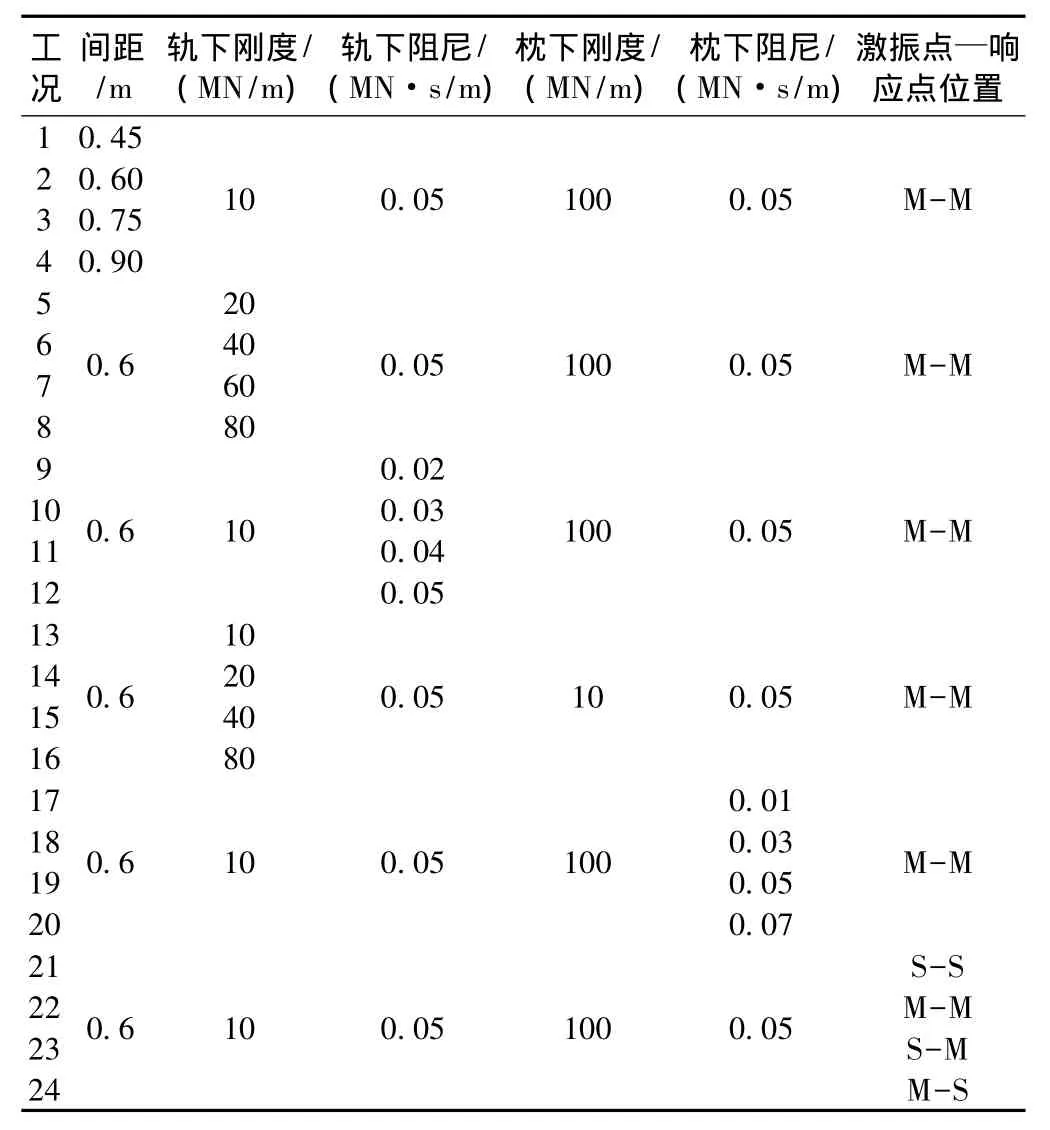
表2 轨道结构参数的取值情况

表2中，“S－S”指激振点与响应点同处于弹性支撑正上方，“M－M”指激振点与响应点同处于相邻支撑跨中，“S－M”指激振点位于弹性轨下支撑上方，响应点处于相邻支撑跨中，“M－S”与“S－M”位置相反。

为便于对比，对不同参数下轨道结构位移频响函数进行计算对比，如图12所示。

由图12得出如下结论。

(1)根据pinned-pinned共振频率fpp计算公式［5］，支撑间距0.9 m轨道结构的一阶pinned-pinned共振频率fpp1=630 Hz，与图12(a)所示一致，再次验证了文中轨道解析模型的正确性。Pinned-pinned共振频率与轨枕支撑间距密切相关，并且成反比例关系;另外，轨枕支撑间距变化引起轨道结构分布刚度发生变化，对其他共振频率略有影响。

图12 轨道结构位移频响函数对比

(2)即使激振点和响应点位置发生变化，轨道系统共振频率ft，钢轨共振频率fr，反共振频率fb－a基本保持不变。Pinned-pinned共振频率点与激振点、响应点位置相关:激振点和响应点分别位于轨下支撑上方和相邻支撑之间时，fpp基本消失;激振点和响应点均位于弹性支撑正上方时，fpp为反共振点;激振点和响应点均位于相邻支撑之间时，fpp为共振点。

(3)轨下支撑刚度对轨道结构钢轨共振频率fr，和反共振频率fb－a影响较大，对轨道系统共振频率ft略有影响，对pinned-pinned共振频率fpp影响不大。

(4)轨下支撑阻尼对轨道结构各响应主频ft，fr，fb－a和fpp都略有影响，但轨下支撑阻尼并不能改变各共振频率点的位置，只能改变其响应幅值。

(5)枕下支撑刚度对轨道系统共振频率ft影响较大，对钢轨共振频率fr和反共振频率fb－a略有影响，对fpp影响不大。随着刚度的减小，ft逐渐减小，ft响应幅值由大变小再变大，而fr，fb－a逐渐减小，响应幅值逐渐增大。

(6)枕下支撑阻尼仅对轨道结构 ft，fr，fb－a的响应幅值有所影响，对其位置没有影响，而对fpp的位置和响应幅值均无影响。

3 结论

基于轨道结构的周期性频域解析模型，结合北京地铁在线锤击试验，通过计算轨道结构在脉冲荷载下的频响函数，对0～2 000 Hz内轨道结构的动力响应主频进行分析;并通过改变轨道结构参数，研究了轨下支撑刚度、阻尼，枕下支撑刚度、阻尼和轨枕支撑间距等对轨道结构各动力响应主频的影响情况。研究结果表明:轨下支撑刚度对钢轨共振频率影响较大，枕下支撑刚度对轨道系统共振频率影响较大，而轨下支撑阻尼和枕下支撑阻尼仅能改变各共振频率点的响应幅值，不能改变其位置;轨枕支撑间距仅对pinned-pinned共振频率影响较大，对其他共振频率点的影响较小。

［1］刘维宁，任静，刘卫丰，等.北京地铁钢轨波磨测试分析［J］.都市快轨交通，2011，24(3):6-9.

［2］Grassie S L，Gregory R W，Harrison D，et al.The Dynamic Response of Railway Track to High Frequency Lateral Excitation［J］.Journal Mechanical Engineering Science，1982，24(2):77-90.

［3］李成辉，万复光.轨道横向动力特性振型叠加法分析［J］.西南交通大学学报，1993(2):65-69.

［4］李德建，曾庆元.直线轨道空间动力特性分析的有限单元法［J］.长沙铁道学院学报，1995，13(1):1-6.

［5］Amnon Pieter DE MAN，A Survey of Dynamic Railway Track Properties and Their Quality［D］.Delft University of technology，2002.

［6］雷晓燕.铁路轨道结构数值分析方法［M］.北京:中国铁道出版社，1998.

［7］刘维宁，张昀青.轨道结构在移动荷载作用下的周期解析解［J］.工程力学，2004，21(5):93，100-102.

［8］苏宇，刘维宁，孙晓静，等.梯形轨道减振性能研究［J］.铁道标准设计，2007(10):71-74.

［9］李克飞，刘维宁，孙晓静，等.北京地铁5号线高架线减振措施现场测试与分析［J］.中国铁道科学，2009，30(4):25-29.

［10］张昀青.地铁列车振动响应及轨道结构参数影响分析［D］.北京:北京交通大学，2004.

［11］李克飞.基于变速及曲线车轨耦合频域解析模型的地铁减振轨道动力特性研究［D］.北京:北京交通大学，2012.