蒙古国及其周边地区地震目录初步分析1
2014-11-26徐伟进高孟潭李宗超
徐伟进 高孟潭 李宗超
(中国地震局地球物理研究所,北京 100081)
前言
地震目录是指按照时间顺序,对地震的时、空、强等参数进行收录,编辑成册的目录资料。地震目录是地震学研究的基础资料,对地震目录的分析研究是地震学研究的基本内容之一。一般来说,地震目录的分析处理主要包括:余震删除、完整性分析、地震的时空特征分析等。
本文通过中蒙两国地震工作者的共同努力,搜集整理得到了蒙古国及其周边地区的地震目录。目前关于对蒙古国地震目录分析处理的工作还比较少见。为了使广大地震科研工作者能够进一步认识蒙古国的地震活动特征,以及使该目录能够方便地应用于蒙古国的地震危险性分析、地震预测等地震学研究中,作者对该目录做了余震删除、时间完整性分析以及时间统计分布特征分析等工作。
当前的地震危险性分析及地震预测模型中,大都将地震时间分布看成是泊松分布(Cornell,1968;高孟潭,1996;胡聿贤等,2001;Kagan等,1994;Frankel,1995)。然而,小区域、短时间内的余震丛集是不符合泊松分布的,这就需要把余震从地震序列中删除。目前的余震删除方法主要有:时空窗法(Utsu,1969;Gardner等,1974)、基于地震事件之间时空距离的链接法(Resenberg,1985)、随机除丛法(Zhuang等,2002)。Wang等(2010)系统比较了几种余震删除方法的差异,结果显示,没有明显的证据表明哪一种方法更有优势。考虑到计算的简便和使用的广泛性,文中作者使用Gardner等(1974)的方法进行余震删除。
地震目录时间完整性分析是地震目录分析的重要工作。在地震预测、地震危险性分析及其它地震活动性研究中,不完整的地震目录会给地震活动性参数的估计带来偏差,因此,在研究一个地区的地震活动性时,分析这一地区地震目录的可靠性是非常有必要的。本文中作者将采用Albarello等(2001)提出的新的统计方法对蒙古国的地震目录进行完整性分析。
地震的时间独立性,即地震发生在时间上是一个泊松过程,是被地震学界广泛接受的假说之一,这一假说是地震危险性分析及其它地震学研究中的最基本理论之一。文中作者采用χ2检验、K-S检验、游程检验(Run-test)对蒙古国地震目录的时间统计分布特征做了初步分析。关于检验方法的详细介绍可参考Gibbons等(2003)的文章。
1 地震目录及研究区
文中采用的地震目录由两套目录合并而成。一套目录是中蒙边境中国一侧的区域台网记录的目录,另一套为蒙古国天文与地球物理研究所记录的目录。由于两套目录中有相同的地震记录,因此在合并前进行了甄选和剔除,并对部分地震进行了重新定位。此外目录中还包含蒙古国根据历史文献记载整理的历史地震目录。目录的起始震级为MS3.5级,记录周期为公元1119—2010年,共计7500条。
图1为蒙古国及周边地区地震目录空间分布图。从图中可以看出,蒙古国地震活动主要集中在中部和西部地区,东部地区地震活动较弱且较为分散。图中灰色粗边框以内的地区为文中的研究区域,作者将选取这一区域内的地震目录进行分析。
由于地震台网监测能力的差异,地震目录的完整性在空间上往往是有差异的,因此在进行地震目录的完整性分析时,可采用空间网格划分的方法进行计算。然而蒙古国地震目录样本较少,不适合采用空间网格划分的方法进行计算。因此,文中为了表示地震完整性的空间差异,根据蒙古国的地质构造及地震活动性分布划分了10个研究区域进行地震目录的完整性计算(见图1灰色区域)。图中用编号表示研究区域的名称,如An表示第n个研究区域。其中A0表示整个研究区域。
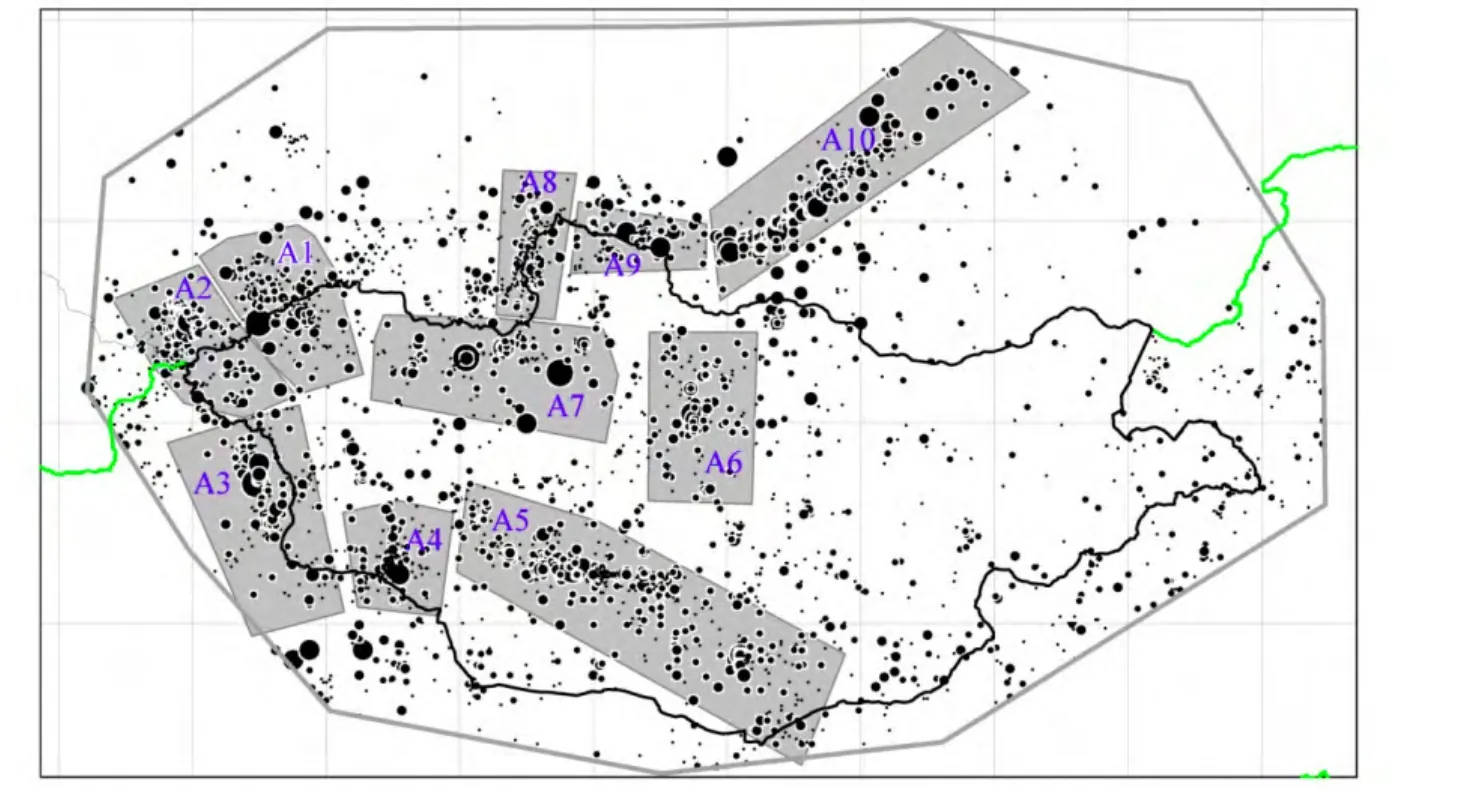
图1 蒙古国地震目录空间分布及研究区示意图Fig. 1 Epicentral distribution of earthquakes(M≥3.5)reported in the Mongolian seismic catalog and study areas(gray areas)
2 地震目录余震删除
在前言中已经简单介绍了地震目录的余震删除方法。在目前的地震活动性研究中,特别是概率地震危险性分析及概率地震预测中,人们普遍采用Gardner等(1974)提出的时空窗余震删除方法,其主要原因是该方法简单易操作,并且具有扎实的数学、物理基础。因此作者也采用这一方法进行余震删除。在该方法中,空间窗口是根据下式确定的(Knopoff等,1972):
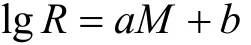
式中,a、b为固定参数值,a、b的取值分别为0.5和-1.78(刘杰等,1996)。时间窗口根据表1给出,震级不在表中的根据线性插值得出。

表1 不同震级地震的余震时间窗(Gardner等,1974)Table 1 Time window algorithm for aftershocks with different magnitudes(Gardner et al.,1974)
图2为删除余震前后地震活动率的对比曲线,可以看出在未删除余震前地震活动率出现几个峰值,这是由于在这一时间有震级较大的地震发生,从而在短时间内产生大量余震事件。而在删除余震后,地震活动率不再有明显的峰值,背景地震活动随时间变化基本平稳。
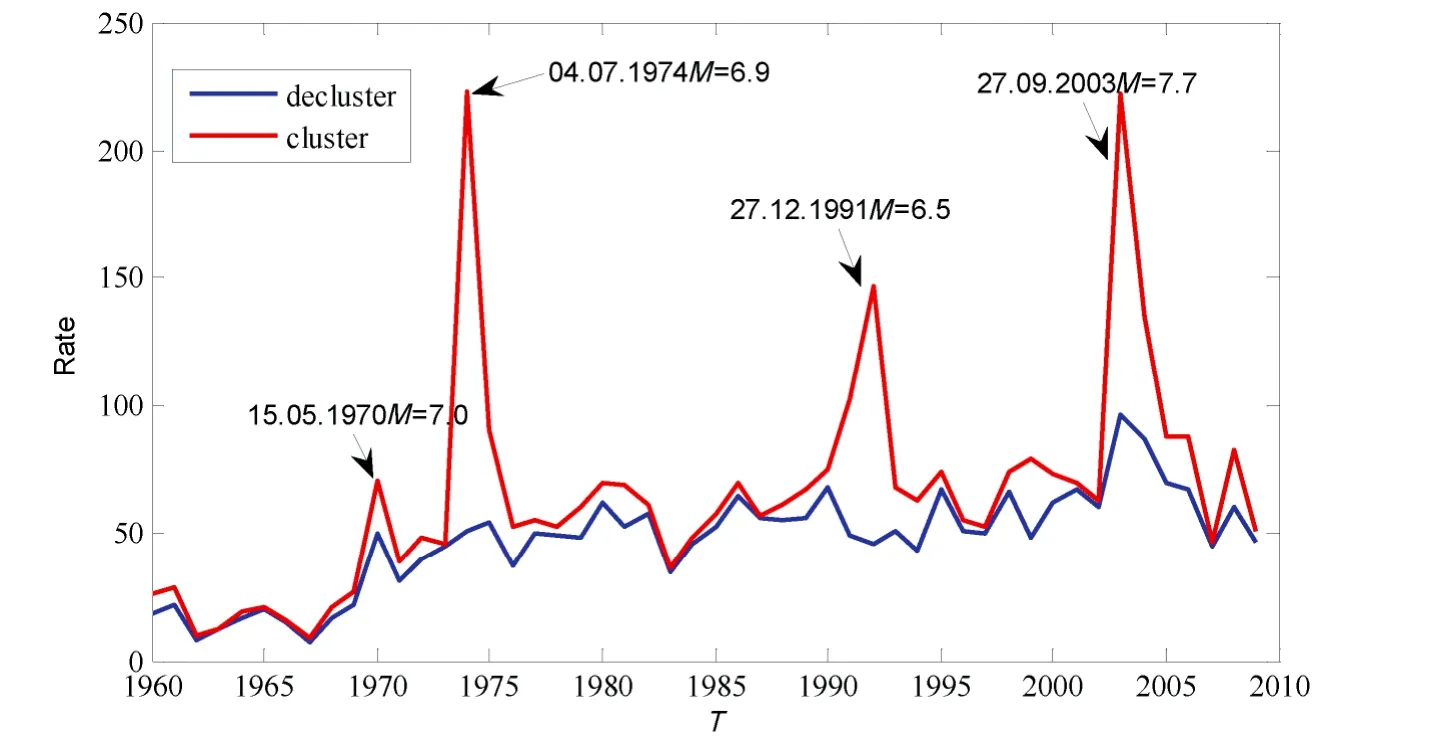
图2 余震删除前后地震活动率比较(M≥3.5)Fig. 2 Seismic rate as a function of time for cluster(red line)and decluster(blue line)catalogs(M≥3.5)
3 地震目录完整性分析
3.1 方法简介
首先采用Albarello等(2001)提出的新的统计方法,分析蒙古国及其周边地区地震目录的完整起始时间。其方法为:
假设一套地震目录是完整的(假设C)、具有代表性的(假设R),则可将计算每年的平均年发生频次作为地震活动率,将其称为样本估计。一般来说,这里计算的地震活动率是符合泊松分布的,但是根据中心极限定理,可以近似将其看作是符合高斯分布的。由于高斯分布的对称性,在两个不同时间段itΔ和jtΔ内观测到的地震活动率in和jn应满足下式:

式中,p是相关概率。
如果接受假设R,即地震的发生是一个独立的过程,那么就认为在ΔT时间段内地震目录是完整的。
为了实现上述假设,首先将地震目录的时间段TΔ以tδ为间隔分成2N个不重合的子段,对于每一子段itδ计算该段内的地震活动率in,基于这些地震活动率定义一个二进制的随机变量D:

实际上,变量D是地震目录前一部分地震活动率和后一部分地震活动率的比较。若D=0的次数较多,就意味着时间较早的地震有缺失,地震目录完整程度下降。
对于N′个可用的地震目录子段,m为D=0的次数。如果目录是完整的,那么实际观测中计算得到的次数大于等于m的概率可用二项式计算:
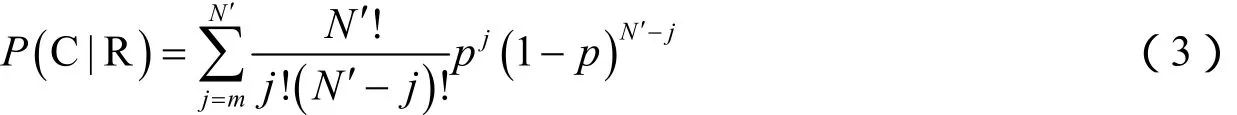
根据式(1),p值取0.5。这一概率主要依赖于假设R的置信程度。概率值越小,意味着目录完整程度越低。
上述过程是地震子目录在整个目录中具有代表性的条件下其完整性的概率。显然希望得到的是某一具体实际段iTΔ内地震完整的非条件概率:表示地震目录在时间段iTΔ内具有统计代表性,即假设R的置信程度。

为了估计假设R的概率,应当考虑地震孕育过程的长期统计特征,当然这一概率并非是一个先验概率,可将假设R的概率简单写为:式中,

式中,ΔTmax是采用的整个地震目录的记录周期;k是一个大于1的定值。
因此,随着ΔTi的增大,是线性递增的。
联合式(3)、(4)、(5),则:

然而一般来说这是很难得到的,因此需要将 Pi值重新标度,用以得到新的完整性函数,即:


这一估计的不确定性可以用四分位来计算:

其中
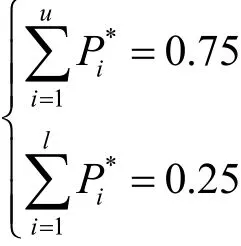
3.2 结果分析
文中主要分析了图1中10个研究区域和蒙古全境MS≥3.5级地震的完整起始时间。此外,还分析了蒙古全境M≥5级和M≥6级地震的完整起始时间。
表2为各研究区地震目录的完整起始时间及其上下限。其中,cT为完整起始时间;uT为不确定性的上限值;lT为不确定性的下限值。从中可以看出,蒙古国MS≥3.5级地震的完整起始时间大都在1970年以后,误差约为±10年左右。对于仪器记录的地震而言,这一完整起始时间相对较晚且离散度较大,这可能与蒙古国台网架设密度及经济、科学技术发展水平有关。蒙古国M≥5.0级地震的完整起始时间约为1945年前后,误差约为±15年;M≥6.0级地震的完整起始时间约为1900年前后,误差约为±30年。可以看出,随着起始震级的增大,完整起始年的误差也越大,这是由于随着震级的增大,地震事件样本长度急剧减小,从而导致了不确定性的增加。其次,对于大地震来说其复发周期很长,从而也导致了其完整起始年不确定较大。
从表2第3列各研究区的地震目录完整起始记录时间可以看出,蒙古国及其周边地区地震目录的完整起始时间具有一定的空间差异,这可能与每个地区地震仪器的布设密度有关。在地震仪器布设密度较大的地区,地震监测能力强,地震的完整起始时间就稍早一些,反之则稍晚一些。此外,与仪器性能、人员素质以及该地区地震地质研究工作开展的早晚等也有一定关系。
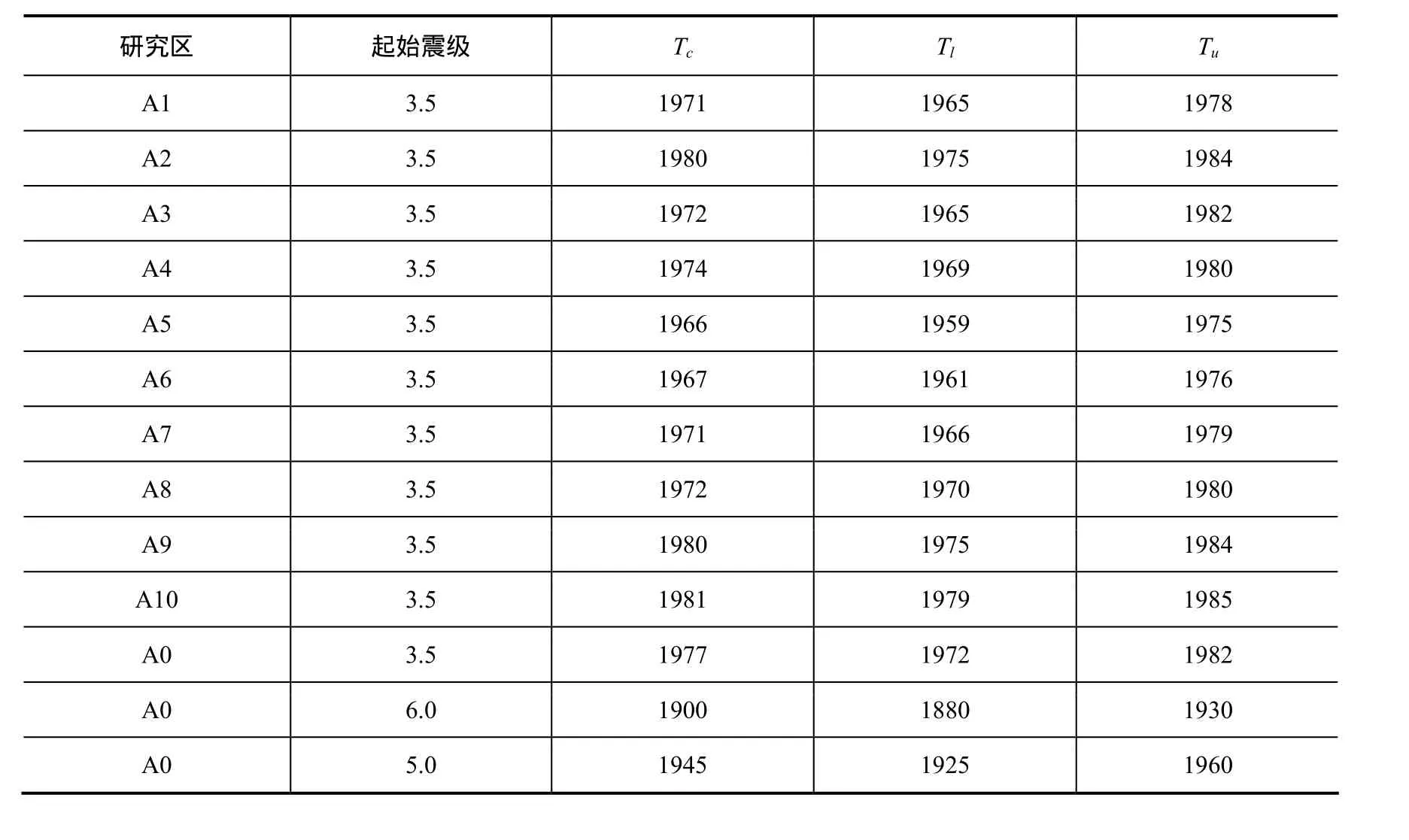
表2 各研究区不同起始震级地震目录完整起始时间 cT及不确定性 uT和 lTTable 2 Completeness timecTvalues and uncertaintyuTandlTvalues for seismic zones
4 地震目录时间统计特征分析
地震的时间独立性,即地震发生在时间上是一个泊松过程,是被地震学界广泛接受的假说之一,这一假说是地震危险性分析及其它地震学研究中的最基本理论之一。本文以地震时间分布符合泊松分布为零假设H0,采用χ2检验、K-S检验、游程检验(Run-test)对蒙古国地震目录在时间上是否符合泊松分布做了检验。并采用Ripley’s K-function(Ripley,1976;1977)对地震时间的丛集特征做了分析。
4.1 时间独立性检验(Poisson检验)方法简介
(1)2χ检验
2χ检验法是在总体X的分布未知时,根据来自总体的样本,检验关于总体分布假设的一种检验方法。使用2χ检验对总体分布进行检验时,首先提出的原假设为:
H0:总体X的分布函数为F0(x)
然后,根据样本的经验分布和所假设的理论分布之间的吻合程度,来决定是否接受原假设时间相关性检验。2χ检验的基本步骤为:
②将落入第k个小区间 Ak的样本值的个数记作 nk,称为实际频数。
③根据所假设的理论分布,可以算出总体X值落入每个kA的概率kp,于是,knp就是落入kA的样本值的理论频数:

如何表示实际频数与理论频数的差异,Pearson(1900)引入了如下统计量来表示经验分布与理论分布的差异:

2χ检验比较的是经验分布与理论分布概率密度函数的差异,并且在实际应用中第一步小区间间隔的选取是十分重要的。具体2χ检验方法可参考《应用统计学》(倪加勋等,1993)。
(2)Kolmogorov-Smirnov(K-S)检验
Kolmogorov-Smirnov检验是用来检验一组具有未知分布XF的随机数是否来自某一个特定连续的分布函数0F,其原假设为:
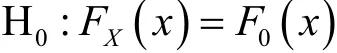
Glivenko-Cantelli theorem (Gibbons等,2003) 认为,样本的经验分布函数(empirical distribution function) Sn(x)在所有的x值处为)提供了点估计。因此在样本容量较大时,经验分布函数值与真实分布函数值的差别是很小的。因此Kolmogorov-Smirnov检验的统计量可写为:
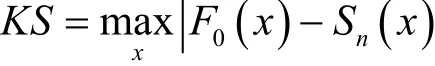
同样在给定显著性水平α后,可通过查表获得统计量在该显著性水平下统计量的临界值。关于K-S检验的方法可参考Gibbons等(2003)的文章。
(3)游程检验(Runs-test)
游程检验是一个以随机过程为平稳的且不具有自相关性为原假设的检验方法。在任何一个由实数组成的时间序列里,一个游程是指一个连续不间断的且具有相同符号的数值组成的子序列,并且时正、时负交替进行。这里需要特别指出的是,可以考虑关于样本均值的游程随机性,对于大于均值的数据将其定为正号,小于均值的数据定为负号。假设有N个数据,其中p个定为正号数据,n个定为负号数据,那么,得到的游程个数小于等于观测值R的概率为:
若 n, p都大于10,那么R的分布可以近似看成符合以均值为,方差为的高斯分布,显然,可以将该正态分布写成统计量为
(4)K-function丛集检验
一种广泛应用于估计单一点过程在时间和空间上是否丛集的方法为 Ripley’s K-function(Ripley,1976;1977)。其定义为:

式中,λ为单位时间或面积内的事件数目,即事件密度(intensity)。对于一维的时间点过程K-function,可用下式进行计算:

式中,L为总的时间段;n为总的观测事件数;t为时间;ijd为时间i和时间j之间的间隔;I等于1,若ijd<t,否则为0;ijw为边界修正项。
为了更加直观地表现出点过程在不同时间尺度上的分布特征,Hwang(2005)提出了关于时间点过程的L函数:

4.2 结果分析
表3为采用三种检验方法进行检验得到的结果,可以看出采用游程检验和卡方检验,在显著性水平α=0.05和α=0.01的情况下,均接受地震目录在时间上符合泊松分布这一假设。只是采用卡方检验时p值小于0.1,接受H0的理由不是很强。采用K-S检验,在显著性水平α=0.05时不接受H0,在α=0.01时接受H0,由此可以看出接受H0的理由是比较弱的。
上述检验结果表明,蒙古国及其周边地区地震目录符合泊松分布的理由是不够强的。这可能是由于背景地震活动的时间非平稳性决定的。为此,作者采用时间K-function分析方法研究了蒙古国及其周边地区地震目录的时间丛集特征。为了更加直观地表现出地震事件的时间丛集特征,往往把K-function换算成L-function。关于K-function分析方法的具体介绍可参考徐伟进(2012)的博士论文。
图3为蒙古国及其周边地区地震目录L-function随时间的变化曲线。图中黑线表示泊松分布L(t)-t的理论值。实测数值若在黑线之上表示事件具有时间丛集性;实测数值若在黑线之下则表示事件分布为规则分布,实际计算中这一现象往往是由边界效应造成的。图中红线为采用未删除余震的地震目录计算得到的L(t)-t值,可以看出未删除余震地震目录的L(t)-t值基本在黑线之上,说明地震目录在时间上是丛集的。一般认为,L(t)-t值的峰值所对应的时间为丛集周期,因此,从红线可以看出未删除余震的目录具有6年和15年左右的丛集周期。图3中蓝线为删除余震后地震目录的L(t)-t值,可以看出蓝线在6年左右的时间点对应一个峰值,而后L(t)-t逐渐减小,趋近于黑线。这意味着,即使在删除余震后,地震目录仍具有6年左右的丛集周期,说明蒙古国及其周边地区地震活动具有时间非平稳性。

表3 删除余震后的地震目录卡方、K-S及游程检验结果Table 3 Result of χ2-test,K-S test,Run-test for decluster catalog

图3 蒙古国地震目录时间L-function变化曲线,红色曲线为未删除余震的地震目录的L-function变化曲线,蓝色曲线为删除余震后的地震目录的L-function变化曲线,黑线为泊松分布L-function理论值Fig. 3 L(t)-t value as a function of time for cluster (red curve) and decluster(blue curve) catalog. Black curve shows theoretical result of Poisson Model
5 结论与讨论
通过上述对蒙古国及其周边地区地震目录的初步分析,作者认为,蒙古国 M≥3.5级地震完整记录起始时间为1977年;M≥5.0级地震完整记录起始时间为1945年;M≥6.0级地震完整记录起始时间为1900年。地震目录完整记录起始时间具有一定的空间差异,这可能与每个地区地震仪器的布设密度有关,在地震仪器布设密度较大的地区,地震监测能力强,地震的完整起始时间就稍早一些,反之,则稍晚一些。此外,与仪器性能、人员素质以及该地区地震地质研究工作开展的早晚等也有关系。
研究还表明,删除余震后蒙古国地震活动随时间变化基本平稳,时间统计分布特征符合泊松分布。但是在删除余震后,蒙古国地震活动仍有6年左右的丛集周期,这说明蒙古国及其周边地区地震活动具有时间非平稳性。地震活动在时间上表现出的非平稳性,可能是由于一下几个方面的原因造成的:①在强震发生后,其形成的破裂带会长期控制该区域的地震活动特征,从而地震活动呈长期丛集;②地震构造的活动速率(如:滑移、蠕动等)是随时间变化的(Lombardi等,2007);③区域或全球范围内长期应力变化的相互影响(Ogata等,1991)。因此,在以后的地震危险性估计中为了更加科学合理地估计地震活动率,应当充分利用地球物理、大地测量、地球动力学等方面的资料对地震的活动趋势进行研究,以减小地震活动的非平稳性对地震活动率估计值的影响。
本文的研究结果可以供其他学者进行对比研究使用,得到的完整的地震目录可以作为地震学研究的基础资料。
高孟潭,1996. 基于泊松分布的地震烈度发生概率模型. 中国地震,12(2):195—201.
胡聿贤,高孟潭,2001.《中国地震动参数区划图(GB 18306-2001)》宣贯教材. 北京:中国标准出版社.
刘杰,陈棋福,陈颙,1996. 华北地区地震目录完全性分析. 地震,16(1):59—67.
倪加勋,袁卫,易丹辉,蔡志洲,1993. 应用统计学. 北京:中国人民大学出版社,262.
徐伟进,2012. 地震危险性分析中地震时空统计分布模型研究 [博士学位论文]. 中国地震局地球物理研究所.
Albarello D.,Romano Camassi and Alessandro Rebez,2001. Detection of Space and Time Heterogeneity in the Completeness of a Seismic Catalog by a Statistical Approach:An Application to the Italian Area. Bull. Seism. Soc.Am.,91(6):1694—1703.
Cornell C.A.,1968. Engineeing seismic risk analysis. Bulletin of the Seismological Society of America,58:1583—1606.
Frankel A.,1995. Mapping Seismic Hazard in the Central and Eastern United States. Seismol. Res. Lett.,66:8—21.
Gardner J.K. and Knopoff L.,1974. Is the Sequence of Earthquakes in Southern California,with Aftershocks Removed,Poissonian? Bull. Seism. Soc. Am.,64(5):1363—1367.
Gibbons J.D. and Chakraborti S.,2003. Non-parametric Statistical Inference.Boca Raton,Fla.:CRC Press.
Hwang Sungsoon,2005. Extending Spatial Hot Spot Detection Techniques to Temporal Dimensions. Environment and Planning B Planning and Design,36(5):865—882.
Kagan Y.Y. and Jackson D.D.,1994. Long-term Probabilistic Forecasting of Earthquakes. J. Geophys. Res.,99:13685—13700.
Knopoff L. and Gardner J.K.,1972. Higher Seismic Activity during Local Night on the Raw Worldwide Earthquake Catalog. Geophys. J.,28:311—313.
Lombardi A.M. and Marzocchi W.,2007. Evidence of Clustering and Nonstationarity in the Time Distribution of Large Worldwide Earthquakes. J. Geophys. Res.,112:B02303,doi:10.1029/2006JB004568.
Ogata Y. and Abe K.,1991. Some Statistical Features of the Long-term Variation of the Global and Regional Seismic Activity. Int. Stat. Rev.,59:139—161.
Pearson K.,1900. On the criterion that a system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Phil. Mag. Ser. 5,50:157—175.
Ripley B.,1976. The Second-order Analysis of Stationary Point Processes. Journal of Applied Probability,13(2):255—266.
Ripley B.,1977. Modelling Spatial Patterns (with discussion). Journal of the Royal Statistical Society,Series B 39:172—212.
Resenberg P.,1985. Second-Order Moment of Central California Seismicity,1969-1982. Journal of Geophysical Research,90(B7):5479—5495.
Utsu T.,1969. Aftershock and Earthquake Statistics(I):Some Parameters Which Characterize an Aftershock Sequence and Their Interrelations. Journal of the Faculty of Science,129—195.
Wang Q.,Jackson D.D. and Zhuang J.,2010. Are Spontaneous Earthquakes Stationary in California? J. Geophys.Res.,115:B08310,doi:10.1029/2009JB007031.
Zhuang J.,Ogata Y. and Vere-Jones D.,2002. Stochastic Declustering of Space-time Earthquake Occurrences. J. Am.Stat. Assoc.,97:369—380.
