基于牛顿法的电力系统最优潮流计算

朱雪凌，张翠影，赵臣鹏，刘林飞

(华北水利水电大学，河南 郑州450045)

牛顿法具有较好的收敛性，在解最优潮流时必须用到Hessian 矩阵［1］的逆矩阵，其存储量及计算量大，使问题变得复杂，因而如何简化成为首要问题.

1984年，台湾学者Sun D I 等［2］提出应用二次罚函数的牛顿法处理该问题. 该算法不用区分状态变量和控制变量，充分利用电力网络的物理特征，运用Hessian 矩阵的导纳稀疏结构，把等式约束条件和不等式约束条件［3］用Lagrange 乘子引入到目标函数中，直接对拉格朗日函数的Karush-Kuhn-Tucker 条件［4］(简称KKT 条件)进行牛顿法迭代求解，不等式约束用二次罚函数来处理. 文中采用二次罚函数的牛顿法来求解最优潮流，并经试验验证了该方法具有很强的实用性及经济性.

1 牛顿法的数学模型

1.1 非线性规划的数学模型

典型的非线性规划问题［5］就是求解目标函数的极大值或极小值问题，文中所求的是极小值，数学模型可表示为:

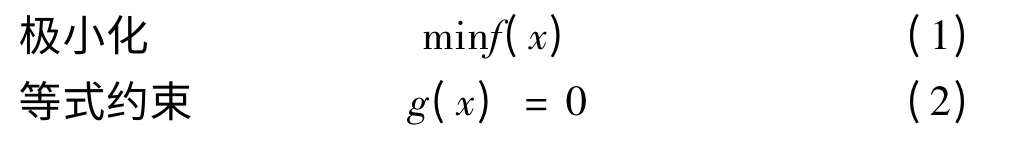
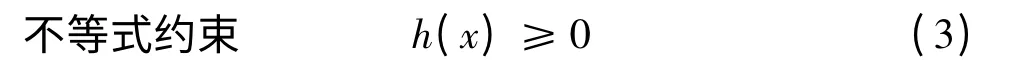
1.2 牛顿法的描述

只考虑等式约束g(x)= 0 时，Lagrange 函数可表示为

其中λ 是Lagrange 乘子［6］，

根据库恩－ 塔克条件［7］，在极小值点(x*，λ*)进行Taylor 展开:

将二次项及高次项忽略，式(5)变为

式中H 和J 分别为Hessian 和Jacobian 矩阵.

将等式约束g(x)= 0 在变量初始值x0处进行Taylor 展开:

忽略二次项与高次项得:

由式(6)和式(7)得:

式(8)则为求等式约束非线性规划问题的牛顿修正方程式［8］.而不等式约束条件h(x)≥0，用二次罚函数［9］来处理，扩展后的Lagrange 函数表示为

式中:Ci为罚因子［10］;i 为不等式约束的个数.把

作为扩展目标函数，考虑不等式约束后的牛顿修正方程为

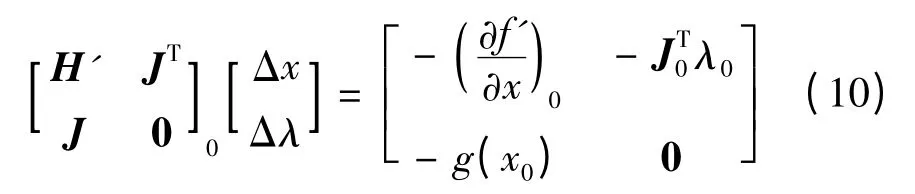
可见，不等式约束只影响Hessian 矩阵系数和等式的右侧.

2 最优潮流的数学模型

2.1 最优潮流

最优潮流(OPF)问题［11］是一个典型的带约束条件的非线性优化问题，进行最优潮流计算时，一般以系统发出有功、无功成本最小为目标函数，其数学模型为

式中fpi(Pgi)，fqi(Qgi)为机组i 的燃料耗费.

2.2 约束条件

等式约束条件为

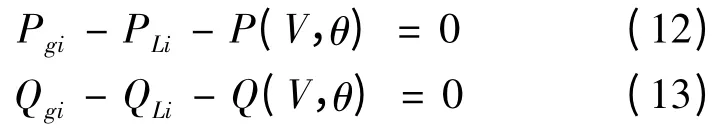
式中:Pgi，PLi分别为机组i 有功出力和有功负荷;Qgi，QLi分别为机组i 无功出力和无功负荷;P(V，θ)，Q(V，θ)分别为有功和无功网损. 式(12)和式(13)也是节点潮流方程［12］.

2.3 不等式约束

不等式约束条件为

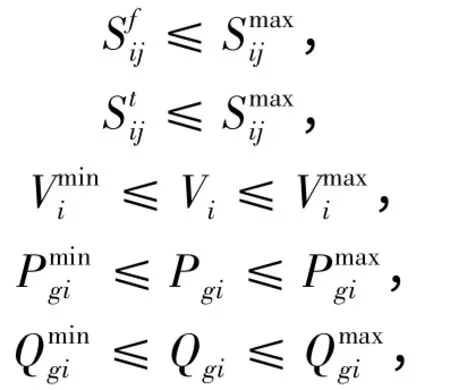
3 算法步骤

算法步骤如下:

1)输入原始数据，给出初始值θ0，V0，λP0，λQ0;

2)节点进行优化排队;

3)形成Hessian 矩阵和Jacobian 矩阵，进行惩罚修正;

4)求解修正方程，得出:

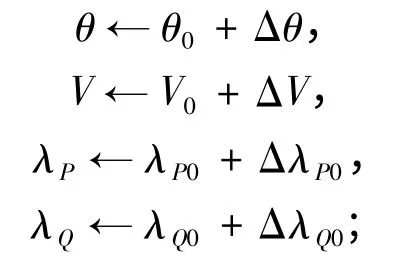
5)求得步骤4 中结果看是否符合库恩－塔克条件，若符合则结束运算，否则返回到第2 步;

6)停止运算.

4 实例计算

以IEEE14［14］节点标准系统为例，运用MATLAB 编程进行最优潮流计算，所得支路节点和母线最优潮流结果见表1和表2. 该算法求得的最优潮流收敛时间在5. 52 s 以内，系统的发电成本为8 081.53 |S/h. 由此可以看出，该算法收敛速度较快，求得的发电成本较低.

表1 支路节点最优潮流计算结果

表2 母线最优潮流计算结果

5 结 语

由试验数据看出:对于复杂的电力系统最优潮流问题，牛顿法可以较为精确地求出计算的结果;用二次罚函数处理不等式约束条件，使复杂问题简单化.同时，二次罚函数的牛顿法的收敛性较好，运算速度较快，求得的发电成本较低，具有很强的经济性与实用性，适合求解大系统的最优潮流问题.

［1］李胜渊.牛顿法最优潮流算法的研究及实践［D］.北京:中国电力科学研究院，1996.

［2］Sun D T，Ashley B. Optimal power flow by Newton approach［J］.IEEE PAS，1984，103(10):401－410.

［3］刘明波.大电网最优潮流计算［M］.北京:科学出版社，2010:385－390.

［4］范宏，韦化.基于扰动KKT 条件的原始－对偶内点法和分界点法的最优潮流研究［J］.电力自动化设备，2004，24(5):5－9.

［5］胡运洪.非线性最优化问题及其算法研究［J］.运城学院学报，2003，21(3):9－10.

［6］王永刚，彭世康，靳现林. 牛顿法最优潮流的改进［J］.继电器，2003，31(3):1－5.

［7］葛结根.库恩－塔克定理在微观经济学中的应用［J］.统计与决策，2004(7):47－53.

［8］颜伟，黄正波，余娟，等.牛顿法潮流计算的高效综合稀疏技术［J］.中国电力，2010，43(7):19－23.

［9］赵普泉，侯志俭，吴际舜. 牛顿法最优潮流算法中离散控制量的新处理方法［J］. 电力系统自动化，1999，23(23):37－58.

［10］张力平，何大愚，朱太秀.牛顿法最优潮流与最优无功补偿［J］.中国电机工程学报，1987，7(1):11－18.

［11］林睦纲.电力系统最优潮流新算法的研究［D］.长沙:长沙理工大学，2005.

［12］陈珩.电力系统稳态分析［M］. 北京:中国电力出版社，2007:123－135.

［13］邱道尹，张凌云，顾波，等. 基于径向基神经网络的双馈风力发电机低电压穿越控制研究［J］. 华北水利水电学院学报，2013，34(6):100－105.

［14］IEEE Committee Report. IEEE reliability test system［J］.IEEE Trans PWRS，1979，98(6):2047－2054.