滚塑工艺传热模型的研究进展

刘学军，贾丽亚

（1.北京工商大学材料与机械工程学院，北京100048；2.蓝星有机硅（上海）有限公司，上海201108）

0 前言

与其他塑料成型工艺相比，滚塑工艺的主要缺点是其成型周期长，能耗较大，另外产品尺寸精度难以得到保证。滚塑工艺所采用的树脂原料的热导率都很低，因此外界通过模具与其进行热交换的速率很慢，这就造成了该工艺的成型周期较长。另外，传统的滚塑模具是在加热室里被热空气进行加热，整个机器框架也在吸收热量，因此滚塑工艺的能量利用率比较低，能耗较大。树脂原料颗粒在受热发生熔融的时候，会有大量的气泡陷入液态的塑料层内。如果不去除这些气泡，会削弱塑料成品的力学性能并影响表面美观。因此在全部物料完成熔融后，整个模具还需继续受热，以使得熔融塑料层内的气泡在高温下能有足够的时间消散，至少绝大部分最终被去除掉。这是滚塑工艺成型周期较长的另一个原因。另外在滚塑工艺的冷却阶段，经常会出现冷却速率过快或者模具受到不对称冷却的情形，造成最终的塑料制品产生收缩或翘曲变形。从而使得其外表不美观，尺寸精度难以保证，同时也使得成型周期变长。

因此，为克服上述滚塑工艺的缺点，就必须仔细研究整个滚塑工艺过程的传热机理。而为滚塑工艺建立一个准确的传热理论模型，然后通过数值计算对其进行仿真一直是研究其传热机理的主要方法。特别是在传热模型被实验验证之后，这些数值模拟的结果可用来定量地分析所有工艺参数对滚塑成型周期的影响，从而为滚塑工艺过程的最优化控制提供理论依据。

本文首先从传热学的角度对滚塑工艺的各个阶段进行解释说明。然后综述了近年来国内外学者为滚塑工艺所建立的传热理论模型以及数值计算结果。将现有传热模型分为tumbling模型、static bed模型和混合模型这3大类，对各类模型的特点进行了分析和比较。并仔细研究了造成现有传热模型仿真精度不高的主要原因。最后指出了在未来相关研究工作中所需要解决的问题和改进的方向。

1 滚塑工艺的传热过程

如图1所示，滚塑工艺中内部空气的温度随时间的变化曲线是对滚塑工艺进行过程控制和优化的主要依据［1］，因此分析该曲线是对滚塑工艺的传热机理进行研究的第一步。根据内部空气温度曲线的形状一般可将整个滚塑工艺分为6个阶段。第一段AB段是从模具和物料开始受热到物料开始发生熔融。在该过程中，外部加热介质与模具的外壁面进行对流换热，热量通过导热方式从模具的外壁面传递到其内壁面。同时模具的内壁面又与物料和内部空气进行对流换热，使其温度升高。当然物料和内部空气之间也存在对流换热，同时在物料内部还存在颗粒与颗粒之间的传热。第二段BC段是从物料开始熔融到全部物料完成熔融，即全部物料都变成液态的熔融塑料层。在这个过程中，熔融塑料是一层接着一层地沉积涂抹在模具的内壁面上，同时向内部推进的熔融塑料层的前沿还与未熔融的且随着模具翻滚的物料继续进行对流换热，这是一个导热、对流换热与相变耦合的传热问题。第三段CD段是从全部物料都完成熔融后，模具被继续加热直到内部空气温度达到某个最大值为止。由于液态塑料的黏性很大，几乎没有流动，因此在这个过程中熔融塑料层可以被看成是与模具内壁面保持紧密静态接触的导热层。此时模具的内壁面是以导热方式将热量传递给熔融的塑料层，而后者与内部空气发生对流换热。以上这3个阶段统称为滚塑工艺的加热阶段。

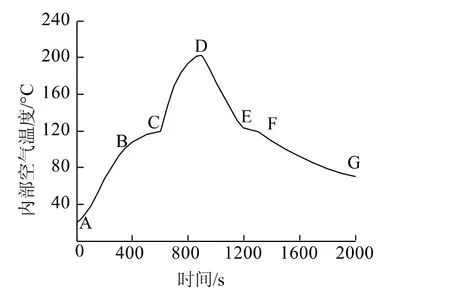
图1 滚塑工艺内部空气温度随时间的变化Fig.1 Variation of internal air temperature with time in rotational molding process

第四段DE段是从内部空气达到最高温度开始到熔融塑料开始结晶固化为止。当整个模具刚开始受到冷却时，虽然其温度是下降的，但内部空气的温度还会继续增加。因此内部空气的最高温度比模具的最高温度要滞后一点时间才会出现。本质上第四段DE段的传热机理与第三段CD段是相同的，惟一的区别就是热传递的方向相反。第五段EF段是从熔融塑料开始结晶固化到全部完成为止。在这一过程，整个塑料层内部存在着导热和结晶固化相变，同时未结晶的熔融塑料与内部空气之间还发生着对流换热。第六段FG段是从全部熔融塑料都完成结晶固化开始，整个模具继续被冷却直至内部空气温度降低到取模温度为止。在这一过程如果不考虑塑料制品在冷却中发生收缩变形从而与模具脱离的情形，那么其传热机理与第四段DE段几乎是一样的。惟一的差别是在第四段DE段塑料层是液态的导热层，而在第六段FG段塑料层是固态的导热层。但如果需要考虑塑料制品与模具脱离的情形，那么第六段的传热机理会变得更加复杂。第四段、第五段、第六段合起来统称为滚塑工艺的冷却阶段。

综上所述，滚塑工艺是将导热、对流换热和相变耦合在一起的传热过程。另外随着塑料形态的变化—物料颗粒、熔融塑料、结晶固化塑料，其热物性参数在发生变化，而且在冷却阶段塑料制品还会发生变形。因此其传热机理是十分复杂的。如下所述，很多国内外学者已对滚塑工艺进行了大量的理论和实验研究以建立一个准确的传热模型并对其进行数值仿真。

2 以往研究工作的综述

国内在滚塑工艺传热模型方面的研究，起步较晚，数量也不多。郭同凯［2］和高镱等［3］分别为滚塑成型工艺建立了传热模型。在这些模型里给出了描述传热过程的控制微分方程以及热边界条件和初始条件。但这些文献里都没有给出任何理论分析解或数值计算结果。

高桂天等［4］研究了卡车翼子板在铝制模具里的滚塑成型工艺。为其建立了一维直角坐标的非稳态导热方程和相变方程，并得出了滚塑成型加热时间的理论计算公式。该加热时间的理论值与实测值之间的平均误差不超过15%。何跃龙等［5］研究了一个中空的圆柱体绕其中心线进行单轴旋转的滚塑工艺的加热过程，并得出模具加热时间和温度场计算的解析解。为简化问题，他们不考虑物料颗粒在模具中的运动情况，而且假设物料一旦开始熔融，即与模具内壁面的所有部分保持静态接触。另外，他们假设物料的温度场沿圆周方向和轴向都是均匀的，只沿径向发生变化。因此他们给出的控制方程为简化后采用一维圆柱坐标描述的非稳态导热方程和相变方程。但是他们没有就某个实际问题给出具体的计算结果。文献［4］和［5］都没有研究滚塑工艺的冷却阶段。

宋本超［6］采用ANASYS有限元软件计算了在滚塑成型工艺中，液态树脂沿轴向进入一个高速旋转模具中的流动前沿位置和充模时间。但是该研究只考虑了树脂的流动，而没有对其进行传热分析。彭威等［7］应用FLUENT软件对滚塑机烘箱内部的温度场进行了数值模拟研究。在计算中采用RNGk-ε湍流模型将三维的速度场和温度场耦合起来求解。但是该研究的主要目的是优化改进滚塑机烘箱的内部结构以使得模具周围热气流的平均温度更高，而并未涉及到模具内部区域的传热分析与计算。

如图2所示，刘学军［8］为一个球形中空塑料制品的滚塑成型工艺的加热过程建立一个更为复杂、完整的理论模型。该模型假设在整个滚塑工艺过程，树脂总是紧密地静态地黏着在模具内壁面上形成一层均匀的塑料导热层。即不考虑塑料粉末以及随后熔融塑料的流动，但考虑内部空气的流动。该模型的计算区域包括模具、塑料导热层和内部空气，因此这是一个将模具的导热、塑料层的导热及其随后的熔融相变和内部空气的对流换热耦合起来求解的传热模型。采用该模型不需假设模具内部的任何对流换热系数，当然由于计算区域的扩大，其计算量会增加一些。

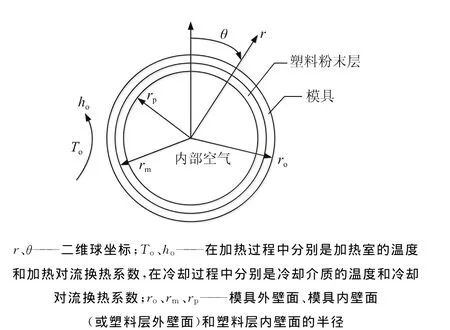
图2 滚塑工艺的传热模型Fig.2 Heat transfer model of rotational molding proess

采用SIMPLE算法通过FLUENT软件对该模型进行了求解，从而数值仿真了滚塑工艺的加热阶段。加热时间的计算结果与实验结果之间的相对误差不超过10%。另外还利用该传热模型定量研究了不同加热温度、对流换热系数等因素对滚塑加热时间的影响。随后上述模型还被应用到包括加热和冷却阶段的整个滚塑工艺过程中［9］。并将整个过程中模具温度和内部空气温度的计算结果与其实验结果相比较，发现二者吻合都较好，从而验证了该传热模型的有效性。另外该模型还被用来定量地研究了加热温度、加热对流换热系数和冷却对流换热系数对不同厚度塑料制品的滚塑成型周期的影响。

国外在滚塑工艺传热分析方面的理论研究开始得较早，文献数量也较多。Rao等［10］最早对滚塑工艺进行了数值模拟。他们建立了一个复杂的理论模型来描述模具内物料颗粒的流动及其与传热过程之间的相互作用，但是该模型的理论计算结果与实验结果之间吻合得不好。随后Throne［11］在所建立的模型里首次提出物料始终与模具内壁面保持静态接触的假设。这个假设使物料颗粒的运动仿真变得没有必要了，因此大大简化了滚塑工艺的传热分析，这就是所谓的static bed模型。相对于Rao等的模型，static bed模型的理论计算结果与实验结果吻合要好一些。

Nugent等［12］为滚塑工艺建立了一个三维的叠加的传热模型，该模型考虑了物料颗粒相对于模具的运动情况，以确定在任意瞬时物料颗粒与模具内壁面的接触位置。基于该模型，他们为滚塑工艺建立了一套称为ROTOSIM的专用仿真程序。采用该程序分别计算了钢制和铝制模具2种情况下，模具的温度、物料的温度、内部空气的温度以及物料完成熔融所需的加热时间和完成整个工艺所需的成型周期。另外他们测量了数值计算所需的模具与外部环境之间的对流换热系数，还测量了上述温度以及加热时间和成型周期的实验值。比较的结果发现对于加热时间，该模型的计算值与实测值吻合较好，最大误差不超过15%。对于模具温度和内部空气温度，其计算值与实测值在加热阶段吻合较好，但在冷却阶段误差却较大，特别是在熔融塑料开始结晶固化之后，误差越来越大。

Sun等［13］采用物料与模具内壁面保持静态接触的假设（static bed模型）分别数值模拟了滚塑工艺内部加热和内部冷却的情形。结果发现内部加热技术可以有效地缩短成型周期，而内部冷却技术可以使得塑料制品内部结构更均匀，减少翘曲变形。但不足的地方是他们在模拟这2种情形时都是将内部空气设成是不随工艺过程变化的恒定温度值，这与实际情形有很大差别。当然这样简化处理的好处是计算量比较小，因为计算区域可以不包含内部空气，但仍需要假设内部空气与塑料层内壁面之间的对流换热系数。

Gogos等［14-15］为整个滚塑工艺过程建立了一个新的传热模型，即所谓的tumbling模型。与前述static bed模型不同的是，他们认为在图1的第一阶段，全部物料颗粒与模具内壁面发生对流换热；而在第二阶段，未熔融的物料颗粒与粘在模具内壁面上的已熔融塑料层发生对流换热。也就是说在这2个阶段，物料颗粒与模具内壁面或熔融塑料层的内壁面没有保持静态接触，因此它们之间的传热方式也不再是导热。为了简化问题，在数值仿真该对流换热过程时，该模型并不考虑物料颗粒在模具内的流动情况。而是假设物料颗粒混合非常均匀，即不考虑物料内部的传热和温度梯度，整个物料只有一个随时间变化的温度。这样就可以在模具或已熔融塑料层的内壁面上采用第三类热边界条件，当然前提是先要假设翻滚的物料与上述内壁面之间的对流换热系数。另外，为使控制微分方程封闭，还必须为物料建立热平衡方程。由于内部空气的热容远小于物料的热容，因此为简化计算，在该热平衡方程中忽略了内部空气的热容。这样的简化处理使得该模型无法计算第一和第二阶段的内部空气温度，但可以计算这2个阶段的物料温度。在全部物料都已熔融之后的其余各段，该模型还是采用塑料层与模具内壁面保持静态接触的假设，在这一点上与static bed模型又是相同的。

该模型采用有限差分法进行数值计算。假设聚合物是在一个特定温度下发生熔融和结晶，并采用界面跟踪法来求解此熔融和结晶相变问题。他们利用无量纲量分析研究了各工艺参数和物性参数对滚塑工艺加热时间和成型周期的影响。另外在进一步简化的前提下，他们还给出了适用于从开始加热到全部物料完成熔融期间的集总参数模型，并由该模型推导出了2种分析解，可用来近似计算滚塑工艺的加热时间。在结晶固化开始之后的过程中，由于塑料的密度开始增加，体积开始减小；另外由于急冷或非对称冷却，因此除非采用特殊工艺比如内部加压技术，否者一般情况下塑料制品都会发生收缩变形或翘曲，从而与模具脱离开来，并与模具内壁面之间产生一层空气间隙。该空气间隙是不良导热体，会在一定程度上削弱塑料制品通过模具向外界环境的传热，从而延误了冷却阶段的结束并使得成型周期变长。该文将此空气间隙层包含在其传热模型的计算区域里并通过数值模拟定量地研究了上述的收缩变形或翘曲对滚塑成型周期的影响。

Olson等［16］也采用上述的tumbling模型，通过有限元方法对一个铝制模具的滚塑工艺的加热阶段进行了数值模拟。他们采用任意拉格朗日欧拉（ALE）算法来仿真熔融塑料层的增长过程。所给出的加热时间和模具温度的计算结果与其实验结果吻合较好。但他们没有给出在加热过程中内部空气温度的计算结果，也没有研究滚塑工艺的冷却阶段。值得一提的是该文采用了一种测量空模具温度的方法来确定在加热阶段模具与外界环境之间的对流换热系数。具体来说该方法就是通过实验来测量一个内部没有装料的空模具的外表面温度，再假设一个外部对流换热系数并将其输入已有的传热模型以对该空模具进行数值模拟。然后将该模具温度的计算曲线与实测曲线相比较，如果这二者吻合，则可认为该假设值即是模具与外界环境之间实际的对流换热系数。如果这二者不吻合，则不断调整对流换热系数的假设值，继续进行上述比较直至这二者吻合为止。

在绝大多数滚塑工艺的传热模型中，一般只考虑模具及其内部物料和空气与外界环境之间的强迫对流换热。但Ghosh等［17］在其模型中还考虑了加热过程和冷却过程中自然对流换热和辐射换热的影响，其目的主要是为了准确地估计出滚塑制品在整个生产过程中的能耗，从节能的角度为其加热和冷却工艺编排的最优化提供理论指导。在物料熔融之前的过程，他们假设热量通过模具以导热方式传递给物料颗粒，而不是以对流换热方式，这一点与tumbling模型是不同的。

为提高内部空气温度的计算精度，Lim等［18］对上述的static bed模型进行了改进，从而为滚塑工艺建立一个新的二维模型。在从开始加热到物料完成熔融的这一过程，该模型将物料分为2个部分—静态区和混合区。静态区与模具内壁面保持紧密接触，传热方式为导热，界面边界条件为热流密度连续性条件。混合区与内部空气接触，二者之间以对流换热方式传热。内部空气假设为具有集总参数的理想气体，同时与模具内壁面和物料之间进行换热。计算方法采用与重合节点技术相结合的Galerkin有限元方法。在物料熔融开始前的加热过程，内部空气温度的计算值与实测值吻合较好。但在2个相变过程和结晶完成后的冷却过程，二者之间差别较大。而加热时间的计算值与实测值也吻合较好。

为了进一步改进内部空气的计算精度，随后他们在该模型的基础上，又发展了一个二维的多层滑移流动模型［19］以更好地模拟在加热阶段，物料颗粒在模具内翻滚运动的情形和熔融物料以一层叠加一层的方式沉积在模具内壁面上的情形。该模型对于相变问题不采用界面跟踪法，而是采用基于温度的固定域有限元技术以便更真实地模拟树脂原料的非等温相变过程。该模型所计算的第一阶段的内部空气温度与实测值吻合较好。由于滚塑工艺在第一阶段的流动与传热机理十分复杂，因此这一点是该模型的突出之处。但在第二阶段后半部分到第三阶段前半部分以及第五和六阶段，内部空气温度的计算值与其实测值之间的偏差开始变大。对于较厚的塑料制品，此偏差更大。另外他们还通过数值模拟比较了发生收缩变形和未发生收缩变形的塑料制品其内部空气温度曲线的差别。他们认为由收缩变形引起的塑料制品与模具间的空气间隙阻碍了塑料制品向模具的传热，从而造成内部空气温度随时间降低的速率变慢。即该空气间隙使得第六阶段的内部空气温度曲线变得比较平缓，这就解释了为什么大部分实验所测得的第五阶段的内部空气温度曲线并没有显示出一个明显的平台。

Greco等［20］基于焓法为滚塑工艺建立了一个新的传热模型。通过引入总焓的概念将非稳态导热方程转化为包含物料熔融度和结晶度随时间变化率的能量平衡方程。他们利用差示扫描量热仪（DSC）得出了这2个变化率的函数曲线，并将该曲线关系式与上述的能量方程耦合起来求解以建立完整的理论模型。他们这样做的目的是为了在一个连续的温度变化范围内数值仿真物料的熔融和结晶过程，从而更接近滚塑原料树脂实际的非等温相变过程。另外他们假设物料静态地黏着在模具内壁面上形成一层均匀的导热层，因此其与模具内壁面之间采用热流密度连续条件。而该物料层与内部空气之间进行对流换热，同时该换热量与内部空气热能的增加量保持能量守恒。采用该传热模型计算所得的模具和内部空气温度总的来说与其实测值都吻合较好，尤其是在熔融和结晶相变过程中内部空气温度的计算精度大大提高。但是在塑料完成结晶相变之后，模具和内部空气温度的计算值与实测值之间的误差随时间越变越大。

Banerjee等［21］为滚塑工艺建立了一个将static bed模型和tumbling模型二者结合在一起的传热模型。他们认为在物料开始熔融之前，作为一个整体，物料与模具内壁面进行对流换热。从这一点来说，它是前述的tumbling模型。但在物料内部，颗粒与颗粒之间只通过导热方式进行传热。从这一点来讲，其又像前述的static bed模型。为简化计算，他们不考虑壁厚很薄的模具内部的温度差，即对模具采用集总参数法处理。对于内部空气，也采用集总参数法处理，即内部空气只有一个随时间变化的平均温度。他们认为内部空气同时与物料和模具内壁面进行对流换热，即内部空气的能量平衡方程为内部空气热能的增加等于物料对它的换热量加上模具对它的换热量。当物料开始熔融后，则认为物料与模具内壁面保持静态接触，此时该模型又变为纯粹的static bed模型。而内部空气的能量平衡方程也相应地变为内部空气热能的增加等于黏着在模具内壁面上的熔融塑料层对它的换热量。

对于滚塑中的相变问题，他们没有采用前述的界面跟踪法，而是采用基于源项的标准焓法来计算树脂原料的非等温熔融和结晶过程。采用该模型进行数值计算时，除了需要知道模具与外界环境的对流换热系数之外，还要知道模具与物料、模具与内部空气以及物料与内部空气之间的对流换热系数。而后三者很难通过实验测量，主要靠以往的经验数据来假设。另外通过调整对流换热系数，该模型还可以近似数值模拟塑料制品在结晶固化以及随后的冷却过程中由于发生收缩变形而与模具脱离的情形。他们通过MATLAB软件来求解离散后的有限差分方程。为了验证该传热模型的有效性，他们将内部空气温度的计算值与实测值进行了比较。对于壁厚较薄的塑料制品，二者总体上吻合较好，但是随着塑料制品壁厚的增加，二者之间的偏差越变越大。

Sarrabi等［22］采用static bed模型来对滚塑工艺进行传热分析，并采用焓法来计算熔融和结晶相变问题。在空间和时间坐标上采用隐式格式的有限差分来离散方程，最后借助于MATLAB软件进行数值计算。他们计算所得的内部空气温度在加热阶段与其实测值吻合较好，但在冷却阶段特别是结晶固化过程与实测值之间的偏差较大。

Hafsaoui等［23］也是采用焓法来求解滚塑工艺中物料的熔融和塑料的结晶相变问题。他们将模具表面温度的计算值与实测值进行比较，结果发现在物料熔融过程中二者之间的偏差较大，而在结晶过程中二者吻合较好。主要原因是他们将高分子聚合物的非等温结晶动力学原理应用到其传热模型中从而提高了冷却结晶过程的计算精度。具体做法是采用Duffo方法通过Ozawa模型计算出塑料在冷却过程的结晶度，然后建立含有温度、焓增和结晶度等物理量的偏微分方程式，再将此方程与塑料层的非稳态导热微分方程耦合起来求解。

通用英语课程是大学英语课程的基本组成部分，旨在培养学生基本的语言技能，传授基本的语言知识，并增加社会、生活、文化、科学等方面的知识，提升综合文化素养。鉴于新升格本科院校师资力量不足、艺体类本科专业学生的英语水平、能力及学习速度差异较大等实际情况，在通用英语学习阶段，实施“水平分层，同层走班”策略，具体实施方法如下：

Abdullah等［24-25］通过理论和实验方法研究了模具的表面强化换热对缩短滚塑成型周期的作用。为了便于进行比较，他们研究了3种模具：普通模具、具有粗糙表面的模具和表面具有销柱形肋片的模具。采用滚塑工艺数值仿真的专用程序ROTOSIM来计算这3种模具的内部空气温度和成型周期。在该传热模型里，分别通过空模具的实验测量以及理论公式的计算来得出这3种模具表面与外界环境的对流换热系数。理论和实验研究表明具有粗糙表面的模具和销柱形肋片的模具都可以显著地缩短成型周期，而后者效果更好。

计算结果与实验结果的比较表明在全部物料完成熔融之前的加热阶段，内部空气温度的计算值与其实测值吻合较好。但是在随后的过程，这二者之间的误差较大。特别是对于较高炉温下较厚的塑料制品，该误差尤其大。另外成型周期的计算值都比其实测值偏小，对于较高炉温下较厚的塑料制品，前者比后者要小的更多。他们认为由如下2个原因造成了这些误差。一是计算中所采用的模具与外界环境之间的对流换热系数不准确；二是在冷却过程中由于塑料制品发生收缩变形而与模具脱离开来，使得整个滚塑工艺实际完成的时间被大大推迟。但计算所采用的ROTOSIM程序无法数值仿真塑料制品与模具脱离的情形。

Liu等［26］采用tumbling模型来研究在模具表面加装不同形状的肋片对滚塑工艺传热的强化作用。利用ANSYS软件通过有限元方法来进行数值仿真。值得注意的是在物料全部完成熔融之前的过程，他们采用混合平均法来得到物料的热物性参数，即将树脂和空气的热物性参数分别乘以颗粒和其间隙中的空气在整个物料中所占的体积百分比并相加。至于相变计算所需要的热物性参数则通过树脂在加热和冷却过程中的DSC曲线测出。类似于文献［16］，他们也采用实验测量和数值模拟空模具的方法来得出模具与外界环境之间的对流换热系数。但不同的地方在于他们比较计算和实验曲线的基准是内部空气温度，而不是模具表面温度。该文在没有肋片、加装矩形肋片、销柱形肋片和三角形肋片这4种情况下分别计算了内部空气的温度，并与其实测值进行比较。结果发现二者在加热阶段吻合较好，但在冷却阶段偏差较大，内部空气的计算温度总是低于实测温度。

3 现有传热模型的误差分析

前述研究表明针对滚塑工艺传热过程的数值仿真，迄今为止还没有一个较为完善的理论模型。总的来说现有传热模型的计算结果与实验结果相比都还有较大的误差。一般来讲，在以往的研究里，模具外表面温度的计算结果与实验结果吻合的相对较好。但内部空气温度的计算结果与实验结果吻合的较差。加热时间的计算值与其实测值吻合较好，但对于整个成型周期，很少文献将其计算值与实测值进行比较，可能是因为不确定因数较多造成的误差太大。为了便于对造成上述误差的原因进行分析，本文先将现有的传热模型进行如下分类。

3.1 传热模型的分类

从滚塑工艺的第三阶段到第六阶段，现有模型基本上都假设塑料层与模具内壁面保持紧密的静态接触。而对于第一和第二阶段，这些模型采用的假设就各不相同，根据这些不同点，可将现有的传热模型大致分为以下3类。

第一类是所谓的tumbling模型，即在第一和第二阶段将物料看成是混合均匀、具有单一温度的与模具内壁面或熔融塑料前沿进行对流换热的介质。其代表性研究工作有文献［14］、［15］、［16］和［26］等。由于很难通过实验来测量粉末状物料与模具内壁面及熔融塑料前沿的对流换热系数，因此为采用tumbling模型只能对其进行假设，这具有一定的随意性。另外在建立内部混合物的热平衡方程时，为简化问题而忽略了内部空气的热容。因此无法计算第一和第二阶段的内部空气温度，但可以计算这2阶段的物料温度。由于很难通过实验来测得滚塑工艺过程中物料的温度，因此无法通过将其计算值与实测值相比较来验证tumbling模型的有效性。

第二类是所谓的static bed模型，即在第一和第二阶段也假设物料是与模具内壁面保持静态接触的导热层。其代表性研究工作有文献［8］、［9］、［11］、［20］和［22］等。根据计算区域的不同，这些研究工作又可分为2类。一类研究的计算区域只包括模具和物料层，但不包含内部空气。因此在这类研究中，虽然不用假设模具内壁面与物料或内部空气的对流换热系数，但仍需要假设物料层与内部空气之间的对流换热系数。另外也需要建立内部空气的热平衡方程。另一类研究的计算区域不仅包含模具和物料层，也包含内部空气。这是一个流固耦合问题，虽然计算量会大一些，但不用假设模具内部的任何对流换热系数。采用static bed模型在第一和第二阶段会人为地强化模具向物料的传热，从而使得加热过程比实际情况提前结束，即加热时间的计算值比其实测值要小［8］。但该模型所采用的假设只在第一阶段和第二阶段的早期与实际情况相差较大，而前两者在整个滚塑成型周期中所占的百分比较小，因此由其带来的误差应该在工程上可接受的范围内［20］。

第三类是将tumbling模型和static bed模型进行改进并融合在一起的混合模型。其代表性研究工作有文献［18］、［19］和［21］等。前两者的做法是在第一和第二阶段，将物料分为与部分模具内壁面进行导热传热的静态区和与其他部分内壁面进行对流换热的混合区，而静态区和混合区同时与内部空气进行对流换热。后者的做法是在第一阶段，将物料看作是一个整体与模具内壁面和内部空气进行对流换热，但在物料区内部的颗粒之间又是保持静态接触，以导热方式进行传热。从理论上讲，应用混合模型可以提高第一和第二阶段内部空气温度的计算精度。但进行数值仿真前除了先要确定在这两阶段模具分别与物料和内部空气之间的对流换热系数，还需要确定物料区与内部空气在分界面上的对流换热系数。

3.2 影响传热模型仿真精度的原因

由于熔融塑料的黏度很大，可以近似忽略它的流动。因此上述模型在第三到第六阶段关于静态接触的假设应该比较接近实际情况。如果不考虑冷却过程中由于塑料变形引起的与模具脱离的情形，这个假设应该不会产生大的误差。然而对于第一和第二阶段，由于其流动和传热机理的复杂性，上述3种模型所采用的假设和简化处理方法都会带来一定的误差。除此之外，本文认为以下4点也是造成现有传热模型仿真精度不高的主要原因。

（1）数值模拟中采用的对流换热系数可能不准确。模具表面与外界环境之间的对流换热系数对计算结果影响很大。前面讲过目前通常的做法是测量空模具的温度并与其计算结果相比较来确定此外部对流换热系数，但显然所研究的空模具与实际情形相比应该还是有一定差异的。实际上该对流换热系数受很多因素影响，其中包括环境介质的种类、加热和冷却方式、加热室的结构、模具的材料和外形尺寸以及表面特征、模具转动的方式和转速、物料的物性参数和装填量等。这也就是为什么在数值计算中各研究者所采用的对流换热系数彼此间差异比较大。

对于表面具有销柱形肋片的模具，文献［24］还采用CFD软件计算肋片周围的流场，再将其带入理论计算公式来获得模具与外界的对流换热系数。但其仿真结果与实验结果的比较表明这种计算换热系数的复杂方法对提高传热模型的准确性帮助并不大。此外在很多情形下，数值模拟之前还需要先确定模具内部的各种对流换热系数。由于其很难通过实验测出，因此基本上也都是凭经验给出。

（2）对滚塑工艺第二和第五阶段的仿真涉及到对相变传热过程的数值计算。为简化问题，以往很多研究者在其传热模型里都是把物料近似看成是具有单一熔融和结晶相变温度的材料。采用这个假设的好处是可以应用界面跟踪法来计算这2个阶段的相变问题。但实际上DSC实验已经表明滚塑原料树脂的相变过程是在一个温度范围内进行的，在相变时并没有明显的固态与液态的分界面。这就解释了为什么在很多研究中第二和第五阶段的内部空气温度计算值与其实测值相差较大。因此近年来一些研究者开始采用更适合于固液相没有明显分界面情形的焓法来求解其传热模型中的相变问题。他们通过DSC实验得到塑料的熔融度和结晶度与相变温度之间的关系式，然后将其与塑料的非稳态导热方程耦合起来进行求解。这样改进后的传热模型确实可以提高在相变过程中内部空气温度的计算准确度，但由于数值仿真前需要通过实验测量并拟合大量的关于塑料非等温相变的热力学数据，因此使得传热模型的建立更加繁复。

（3）滚塑工艺所用的树脂原料的物性参数如密度、比热容和热导率等，在整个成型过程中都随温度的变化而变化。但实际上迄今为止几乎没有任何研究者在传热模型中真正采用这些物性参数与温度之间的拟合关系式。原因可能是为了简化数值计算，使迭代过程更容易收敛，但肯定也会造成一定的误差。以往的研究者对上述物性参数的处理通常有3种方法。第一种是采用常物性假设，即在计算中将树脂的物性参数近似看成是恒定不变的。第二种方法是在滚塑工艺的不同阶段根据树脂的不同状态——颗粒、熔融或固化，而采用与其相对应的物性参数；或者在不同的温度范围，对树脂采用不同的物性参数。这种方法本质上是将树脂的物性参数随温度变化的连续曲线用分段折线来近似代替。第三种方法是混合平均法。比如在滚塑工艺的第二阶段，密度是根据熔融度计算出来的粉料树脂密度和熔融树脂密度的混合平均值；在第五阶段，密度是根据结晶度计算出来的熔融树脂密度和结晶树脂密度的混合平均值。综上所述，从树脂物性参数的处理上来看，第二和第三种方法的精度肯定要比第一种方法高。

（4）在几乎所有的滚塑工艺的传热数值模拟中，一个值得注意的现象是第六阶段的内部空气温度的计算值总比其实测值偏小。造成该误差的主要原因是以往绝大部分研究者在建立传热模型时都没有考虑塑料制品发生收缩或翘曲变形从而与模具脱离对传热过程的影响。就目前来看仅有3篇文献粗略地考虑了该影响因素，他们的处理方法分别如下。Gogos等［15］假设当所有熔融塑料完成结晶固化时，在模具内壁面和塑料制品外表面之间添加一个新的计算区域用来表示这二者脱离后产生的空气间隙。采用非稳态导热微分方程来描述此间隙层，其厚度按通常情况下滚塑制品结晶固化后体积收缩的百分率来确定。Lim等［19］为空气间隙层假设了一个自然对流换热系数，并在模具和塑料制品之间插入了一个隔热单元体。空气间隙对传热的影响就通过将上述的对流换热系数代入该隔热单元的刚度矩阵里来实现。而Banerjee等［21］并没有在模具和塑料制品之间真的建立一个表示空气间隙的计算区域。而是在一半厚度的塑料制品已经结晶固化后，在模具和塑料制品之间的接触面上假设一个对流换热系数，也就是说将这二者之间的导热热阻用对流换热热阻来替代。从而通过人为地增大这二者之间的热阻以模拟该空气间隙对传热的削弱作用。实际上滚塑制品发生收缩和翘曲变形是一个连续的、逐渐进行的过程，由此产生的空气间隙不会突然出现。另外采用假设的和不随时间变化的内部对流换热系数也肯定与实际情况有偏差。因此上述方法都是简化和近似的处理方法，都会给传热模型带来一定的误差。

4 未来研究工作的展望

根据以往相关研究的综述以及传热模型的误差分析，本文认为未来在滚塑工艺传热模型的建立和发展上应着重进行以下几个方面的研究。

（1）滚塑工艺第一和第二阶段的传热机理最为复杂，特别是其中涉及到了物料颗粒在模具内部的流动，目前很少有研究在建模上考虑过这个因素。为改进滚塑工艺在第一和第二阶段的传热模型，有必要将物料颗粒作为内部空气的离散相来研究颗粒与颗粒之间、颗粒与内部空气之间以及与模具内壁面之间的相互作用。而这些相互作用应同时包括动量和热量的相互交换。当然这样改进后模型的计算量和计算难度都将加大。

（2）在滚塑工艺的第二和第五阶段，采用焓法来求解树脂在一个温度范围内的熔融和结晶相变问题。并将聚合物的熔融热力学和结晶动力学原理与现有的传热模型相结合以提高该模型在塑料相变过程的仿真精度。

（3）将树脂的物性参数随温度变化的拟合关系式直接与传热控制方程和边界条件等耦合起来求解以确定物性参数对传热过程的影响并提高传热模型的仿真精度。当然这种方法会使微分方程的非线性度加大，迭代过程难以收敛，数值计算量增加。

（4）对第五和第六阶段塑料制品逐渐收缩和翘曲这个连续的过程进行精确的数值仿真以减小在这2个阶段内部空气温度和整个滚塑成型周期的计算误差。这里面不仅涉及到计算区域内的传热过程和塑料的结晶相变问题，同时还要综合考虑聚合物的结晶动力学因素。

（5）对滚塑工艺的新技术——内部加压和内部冷却进行数值仿真。实验研究［27-28］已经表明内部加压和内部冷却技术可以缩短滚塑成型周期和减小塑料制品的变形。但目前几乎没有任何文献通过对这2项技术进行准确的数值模拟来研究其对滚塑传热机理和工艺过程的影响。可以预期在为它们所建立的传热模型里，计算区域可能需要扩展到包含内部空气区域，另外也要考虑聚合物的结晶动力学因素。

（6）通过理论或实验方法来获得更准确的模具外壁面与环境介质之间的对流换热系数。比如可以将计算区域的边界向外扩展到离模具外壁面比较远的地方从而将环境介质也包含进计算区域。这样在模具外壁面上不再采用第三类热边界条件，因此也不再需要对流换热系数。当然数值计算量和迭代收敛的难度都会增大。另一种方法是将对流换热系数的实验数据通过传热学相似原理拟合出该换热系数与所有影响因素之间的无量纲准则式。当然如果要扩大该无量纲准则式的适用范围，实验工作量也会大大增加。

5 结语

滚塑工艺是将导热、对流换热和相变耦合在一起的传热过程，其传热机理十分复杂。为滚塑工艺建立一个准确的传热模型并对其进行数值仿真是研究滚塑工艺传热机理的主要方法。由此得出的计算结果和结论可为滚塑工艺过程的最优化控制提供理论依据。以往学者已经在滚塑工艺传热模型的建立和发展上做了大量的研究工作，但迄今为止还未得到一个较为准确的传热模型。现有传热模型可大致分为tumbling模型、static bed模型和混合模型3类。造成其仿真精度不高的主要原因是上述3类模型都对滚塑工艺第一和第二阶段中物料颗粒和内部空气的流动与传热情况做了假设和简化处理。此外，所用的对流换热系数不准确、假设塑料的熔融和结晶过程是在某个单一温度下进行、没有考虑塑料物性参数随温度的连续变化、没有考虑冷却中的塑料制品发生变形与模具脱离也是造成传热模型计算误差的主要原因。为提高传热模型的仿真精度并扩大其适用范围，应改进理论或实验方法以获得更准确的对流换热系数、通过焓法并结合熔融热力学和结晶动力学来模拟塑料的相变过程、将物料颗粒当作内部空气的离散相以考虑其彼此之间以及与模具之间的相互作用、数值仿真塑料制品与模具脱离的情形等。这些都是在滚塑工艺传热模型方面未来的主要研究方向。

［1］Crawford R J.Recent Advances in the Manufacture of Plastic Products by Rotomoulding［J］.Journal of Materials Processing Technology，1996，56（1）：263-271.

［2］郭同凯 .旋转模塑过程的热交换计算机模拟系统［J］.新技术新工艺，1997，（3）：7-9.Guo Tongkai.Heat Transfer Computer-Simulating System of Rotational Molding Process［J］.New Technology and Process，1997，（3）：7-9.

［3］高 镱，王福生，高幼银 .滚塑成型工艺中的传热模型［C］／／2005中国国际滚塑论坛论文集 .北京：中国塑料加工工业协会滚塑专业委员会，2005：62-66.

［4］高桂天，梁 策，史新星，等.滚塑成型加热时间的计算［J］.吉林大学学报：工学版，2008，38（2）：340-343.Gao Guitian，Liang Ce，Shi Xinxing，et al.Heating Time Algorithm for Rotational Molding［J］.Journal of Jilin U-niversity：Engineering and Technology Edition，2008，38（2）：340-343.

［5］何跃龙，丁玉梅，李维维.单轴滚塑成型传热过程的数学建模［J］.塑料科技，2009，37（5）：35-39.He Yuelong，Ding Yumei，Li Weiwei.Mathematical Model of Heat Transfer during Rotational Molding of Single Axis［J］，Plastics Science and Technology，2009，37（5）：35-39.

［6］宋本超.液态树脂高速旋转模塑成型工艺研究［J］.中原工学院学报，2011，22（4）：52-55.Song Benchao.Study on High Speed Rotational Molding Process of Liquid Resin［J］，Journal of Zhongyuan University of Technology，2011，22（4）：52-55.

［7］彭 威，关昌峰，秦 柳，等.滚塑机烘箱内部温度场的数值模拟研究［J］.机械设计与制造，2012，41（9）：105-107.Peng Pei，Guan Changfeng，Qin Liu，et al.Numerical Simulation Study on Temperature Field in an Oven of Rotational Molding Machine［J］， Machinery Design and Manufacture，2012，41（9）：105-107.

［8］刘学军.滚塑成型工艺加热阶段的数值研究［J］.中国塑料，2012，26（11）：88-92.Liu Xuejun.Numerical Study on Heating Phase of Rotational Molding Process［J］，China Plastics，2012，26（11）：88-92.

［9］刘学军.滚塑工艺成型周期的数值研究［J］.中国塑料，2013，27（10）：58-64.Liu Xuejun.Numerical Study on Cycle Time of Rotational Molding Process［J］，China Plastics，2013，27 （10）：58-64.

［10］Rao M A，Throne J L.Principles of Rotational Molding［J］.Polymer Engineering and Science，1972，12（7）：237-264.

［11］Throne J L.Rotational Molding Heat Transfer-an Update［J］.Polymer Engineering ＆ Science，1976，16（4）：257-264.

［12］Nugent P J，Crawford R J，Xu Liang.Computer Prediction of Cycle Times During Rotational Molding of Plastics［J］.Advances in Polymer Technology，1992，11（3）：181-191.

［13］Sun D W，Crawford R J.Analysis of the Effects of Internal Heating and Cooling During Rotational Molding of Plastics［J］.Polymer Engineering and Science，1993，33（3）：132-139.

［14］Gogos G，Olson L G，Liu Xuejun，et al.New Models for Rotational Molding of Plastics［J］.Polymer Engineering and Science，1998，38（9）：1387-1398.

［15］Gogos G，Liu Xuejun，Olson L G.Cycle Time Predictions for the Rotational Molding Process With and Without Mold／Part Separation［J］.Polymer Engineering and Science，1999，39（4）：617-629.

［16］Olson L G，Crawford R，Kearns M，et al.Rotational Molding of Plastics：Comparison of Simulation and Experimental Results for an Axisymmetric Mold［J］.Polymer Engineering and Science，2000，40（8）：1758-1764.

［17］Ghosh K，Garimella S.Dynamic Modeling of Thermal Processes in Rotational Molding［C］／／Proceedings of the ASME Heat Transfer／Fluids Engineering，Summer Conference.New York：ASME，2004：1107-1118.

［18］Lim K K，Lanakiev A，Hull J B.Numerical Modeling for Rotational Molding With Non-Isothermal Heating［J］.Plastics，Rubber and Composites，2003，32（10）：421-430.

［19］Lim K K，Lanakiev A.Modeling of Rotational Molding Process：Multi-Layer Slip-Flow Model，Phase-Change，and Warpage［J］.Polymer Engineering and Science，2006，46（7）：960-969.

［20］Greco A，Maffezzoli A，Vlachopoulos J.Simulation of Heat Transfer During Rotational Molding［J］.Advances in Polymer Technology，2003，22（4）：271-279.

［21］Banerjee S，Yan W，Bhattacharyya D.Modeling of Heat Transfer in Rotational Molding［J］.Polymer Engineering and Science，2008，48（11）：2188-2197.

［22］Sarrabi S，Colin X，Tcharkhtchi A.Kinetic Modeling of Polypropylene Thermal Oxidation During Its Processing by Rotational Molding［J］.Journal of Applied Polymer Science，2010，118（2）：980-996.

［23］Hafsaoui S L，Benziane M，Tcharkhtchi A.Thermal Transfer Simulation Regarding the Rotational Molding of Polyamide 11［J］.Journal of Thermal Analysis and Calorimetry，2013，112（1）：285-292.

［24］Abdullah M Z，Bickerton S，Bhattacharyya D.Rotational Molding Cycle Time Reduction Through Surface Enhanced Molds：Part A-Theoretical Study［J］.Polymer Engineering and Science，2007，47（9）：1406-1419.

［25］Abdullah M Z，Bickerton S，Bhattacharyya D.Rotational Molding Cycle Time Reduction Through Surface-Enhanced Molds，Part B：Experimental Study［J］.Polymer Engineering and Science，2007，47（9）：1420-1429.

［26］Liu S J，Fu K H.Experimental Investigation and Numerical Simulation of the Heating／Cooling Process in Rotational Molding Enhanced With Fins［J］.Journal of Applied Polymer Science，2008，108（3）：1696-1705.

［27］Pick L T，Harkin-Jones E.Effect of Mold Pressurisation on Impact Strength of Rotationally Moulded Polyethylenes［J］.Plastics，Rubber and Composites，2006，35（8）：324-330.

［28］Tan S B，Hornsby P R，McAfee M B，et al.Internal Cooling in Rotational Molding—A Review［J］.Polymer Engineering and Science，2011，51（9）：1683-1692.