热壁面位置对矩形腔内自然对流影响的数值分析

金硕宏， 刘建国， 李 凌， 梁小龙

（1.上海理工大学 能源与动力工程学院，上海 200093；2.华能太仓电厂，太仓 215424）

封闭腔内的自然对流换热在工程实际中有着广泛的应用，比如动力电站中电流母线的冷却、太阳能集热器中水的自然循环、用于变压器油冷却的扁盒自然对流冷却器、半导体电子元器件的冷却等［1］.这些问题中，腔体的壁面可能遭受到突然的温度变化，而温变不是经常发生在整个壁面上.因此，研究局部热边界条件下的自然对流换热问题具有更加实际的意义，不少学者作了与此相关的一些研究.Das等［2］数值研究了表面波度和高宽比对具有波形外壳的腔体内换热的影响.Deng等［3］数值研究了壁面有离散热源的矩形腔内的稳态层流自然对流.Nithyadevi等［4］研究了正方腔侧壁局部加热时水的最大密度效应.李娜等［5］研究了封闭空间内小尺度等温竖板自然对流的三维效应.毛正荣等［6］研究了低温冷柜内空气的自然对流.Corcione［7］数值模拟了二维方腔内的稳态层流自然对流，方腔的底部被加热，顶部被冷却，而侧壁分别维持在各种不同的热边界条件下.以往研究中，矩形腔的高宽比一般都不大，且冷热壁面的分布也没有考虑是否对称，对狭窄矩形腔内的自然对流换热问题研究较少.本文对大高宽比的矩形腔内冷热壁面位于侧壁不同相对位置时的自然对流换热问题进行了数值模拟，按照冷热壁面的相对位置是否左右对称，分析了不同工况下Rayleigh数Ra对矩形腔内流场、温度场及平均Nusselt数Nuav的影响，确定了最大和最小传热率的位置，为工程应用提供了一定的参考依据.

1 数学物理模型

考虑二维矩形腔的物理模型如图1所示.矩形腔尺寸为L×H，顶部和底部壁面为绝热，右侧壁三分之一壁面维持在低温Tc，左侧壁三分之一壁面维持在高温Th，冷热壁面的位置可上下移动，侧壁其余部分为绝热.

图1 物理模型示意图Fig.1 Schematic physical model

假设矩形腔内为稳态层流，流体为常物性牛顿流体，普朗特数Pr取0.71，不考虑辐射，忽略粘性耗散，密度采用Boussinesq假设.描述矩形腔内流动与换热的无量纲控制方程为

各无量纲参数定义为

式中，u，v分别为x，y 方向的速度分量；p 为压力；ρ，ν，a，β，g 分别为流体密度、运动黏度、热扩散系数、热膨胀系数和重力加速度.

问题的边界条件如下：

a.上侧壁：U ＝V ＝0，∂Θ／∂Y ＝0，Y ＝0 或Y＝H／L；

b.左侧壁：U＝V＝0，Θ＝1，X＝0；

c.右侧壁：U＝V＝0，Θ＝0，X＝1；

d.下侧壁：U＝V＝0，∂Θ／∂X＝0，X＝0或X＝1.

本问题采用的数值方法为有限差分法，压力场和速度场的耦合采用SIMPLE 算法，对流项采用QUICK 差分格式，细长腔的高宽比H／L 取为10.

2 计算结果及讨论

首先进行网格无关验证，分别取20×200，30×300，40×400，50×500规格的4套均分网格进行模拟计算，发现当网格数大于30×300后，计算结果可以认为基本相同，因此最终计算采用的网格为30×300.

2.1 温度场和流场随冷热壁面相对位置及Ra 的变化

分别计算了Ra＝103，104，105，106时冷热壁面处于不同相对位置下的温度场和流场.

图2所示为Ra＝103～106时冷热壁面对称分布于左右侧壁上部时的温度场和流场.从图中可以看出，温度场在Ra＝103时的等温线呈竖直方向且分布均匀，说明此时的主要传热机理为导热.当Ra＝104时，等温线开始向水平方向扭曲.当Ra＝106时，等温线几乎完全呈水平.随着Ra 的增大，可以看出在冷热壁面附近形成了明显的热边界层，等温线密集，此时对流换热占了主导作用.细长腔体中部呈水平方向的等温线说明了温度场的变化主要局限于腔体的上部，腔体中下部的流体温度没有受到上部冷热壁面的影响.对于流场，可以看出当Ra 较小时，有一个规则的呈椭圆状的漩涡.随着Ra 的增大，漩涡逐渐增大且形状变得不规则.由于冷热壁面位于细长腔体的上部，浮升力方向向上，因而中下部的流体受冷热壁面的影响较小.

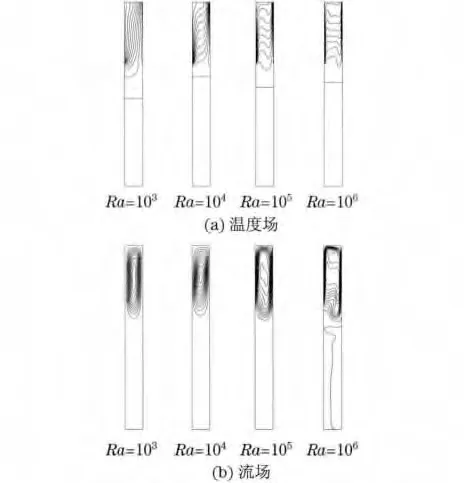
图2 冷热壁面对称分布于左右侧壁上部时的温度场和流场Fig.2 Isotherms and streamlines for top－top heating location

图3所示为Ra＝103～106时冷热壁面对称分布于左右侧壁中部时的温度场和流场.当Ra 较小时，温度场及流场的分布和变化趋势与冷热壁面位于细长腔侧壁上部时相似.但由于冷热壁面远离细长腔的顶部和底部，流体在浮升力的作用下可自由向上向下流动，此时受冷热壁面影响的流体范围要大于位于细长腔侧壁上部时的情形.当Ra＝105～106时，对流换热更加剧烈，细长腔体内的中上部流体都已显著地受到冷热壁面的影响，流场中的漩涡数增加且向细长腔体的顶部扩展.

图3 冷热壁面对称分布于左右侧壁中部时的温度场和流场Fig.3 Isotherms and streamlines for middle－middle heating location

图4所示为Ra＝103～106时冷热壁面对称分布于左右侧壁下部时的温度场和流场.随着Ra 的增大，流体在浮升力的作用下向上流动，等温线和等流函数线迅速向细长腔体的上部扩展.当Ra＝106时，流场中的漩涡已经充满了整个腔体.

图4 冷热壁面对称分布于左右侧壁下部时的温度场和流场Fig.4 Isotherms and streamlines for bottom－bottom heating location

图5所示为Ra＝105时冷热壁面不对称分布时的温度场.当热壁面位于左侧壁上部、冷壁面位于右侧壁中部时，等温线集中在冷热壁面的交界处，这里的温度梯度很大，如图5（a）.随着冷壁面移动到右侧壁的下部，等温线由密变疏，如图5（b）.当热壁面位于左侧壁中部、冷壁面位于右侧壁上部时，冷热壁面处存在着明显的热边界层，如图5（c），此时的对流换热作用很强.当热壁面位于左侧壁下部时，可以看出在冷热壁面附近的热边界层也很明显，如图5（e）和（f）.

图5 冷热壁面不对称分布时的温度场Fig.5 Isotherms for asymmetric distribution of heating locations

图6所示为Ra＝105冷热壁面不对称分布时的流场.其中，图6（a）和图6（b）的流场形态很特别，流场中存在对称的两个漩涡，两个漩涡的中心分别靠近冷热壁面所处的位置.在图6（c）～（f）中已看不到这种现象，此时的流场中有多个漩涡.当热壁面位于中部时，漩涡主要存在于细长腔体的中上部；当热壁面位于下部时，漩涡充满了整个腔体.

2.2 平均Nusselt数Nuav随冷热壁面相对位置及Ra的变化

图7 所示为冷热壁面位于不同相对位置时Nuav随Ra的变化情况.从图中可以看出，无论冷热壁面的相对位置如何，Nuav都随Ra的增大而增大.

对于对称分布时的情形，当Ra＜104时，Nuav随Ra变化的幅度较小，此时传热的主要机理是导热.当Ra＞104时，Nuav随Ra 变化的幅度增大，此时对流换热占主导作用，矩形腔内的流动加剧.在相同的Ra下，可以看出，冷热壁面位于细长腔体中部时的Nuav最大，位于细长腔体上部时的Nuav最小，位于细长腔体下部时的Nuav介于两者之间.

图6 冷热壁面不对称分布时的流场Fig.6 Streamlines for asymmetric distribution of heating locations

对于不对称分布时的情形，以及热壁面位于左侧壁上部的两种情况，Nuav很小，且受Ra 变化的影响也很小；热壁面位于左侧壁中部、冷壁面位于右侧壁上部时的Nuav最大；其它情况下的Nuav介于两者之间.

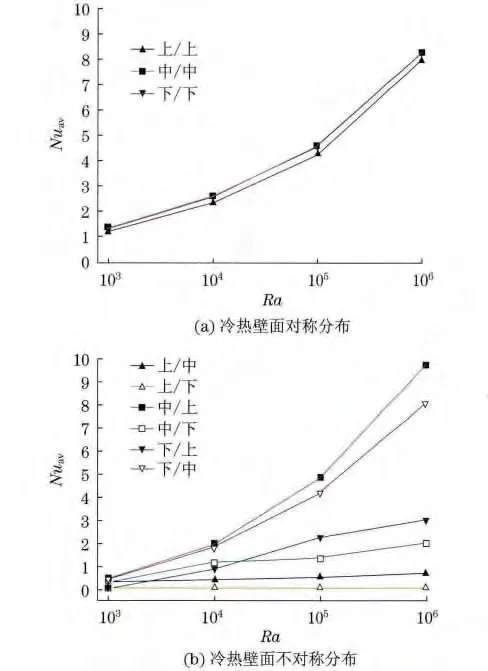
图7 冷热壁面相对位置及Rayleigh数对平均Nusselt数的影响Fig.7 Average Nusselt number for different heating positions and Rayleigh numbers

3 结 论

对细长腔体内冷热壁面位于侧壁不同位置时的对流换热问题进行了数值模拟.模拟结果表明：

a.冷热壁面对称分布时，Nuav是Ra的增函数，并且增幅随Ra 的增大而增大；在相同的Ra 下，冷热壁面位于侧壁中部时的Nuav最大，对流换热作用最强.

b.冷热壁面不对称分布时，在本文所设置的高宽比下，热壁面位于左侧壁中部、冷壁面位于右侧壁上部时的Nuav最大，而热壁面位于上部、冷壁面位于下部时的对流换热作用最小.

［1］Ben N K，Chouikh R，Kerkeni C，et al.Numerical study of the natural convection in cavity heated from the lower corner and cooled from the ceiling［J］.Applied Thermal Engineering，2006，26（7）：772－775.

［2］Das P K，Mahmud S，Tasnim S H，et al.Effect of surface waviness and aspect ratio on heat transfer inside a wavy enclosure［J］.International Journal for Numerical Methods in Heat ＆ Fluid Flow，2003，13（8）：1097－1122.

［3］Deng Q H，Tang G F，Li Y G.A combined temperature scale for analyzing natural convection in rectangular enclosures with discrete wall heat sources ［J］.International Journal of Heat and Mass Transfer，2002，45（16）：3437－3446.

［4］Nithyadevi N，Kandaswamy P，Sivasankaran S.Natural convection in a square cavity with partially active vertical walls：time－periodic boundary condition［J］.Mathematical Problems in Engineering，2006，206：1－16.

［5］李娜，李志信，过增元.封闭空间内小尺度等温竖板自然对流的三维效应［J］.上海理工大学学报，2003，25（3）：218－220.

［6］毛正荣，赵巍，张华，等.低温冷柜内空气的传热与流动特性 研 究［J］.上 海 理 工 大 学 学 报，2003，25（1）：21－23.

［7］Corcione M.Effects of the thermal boundary conditions at the sidewalls upon natural convection in rectangular enclosures heated from bellow and cooled from above［J］.International Journal of Thermal Sciences，2003，42（2）：199－208.