基于EMD 去噪的Prony 算法在电网事故分析中的应用

胡昊明，江叶峰，葛亚明，尤 伟，张宁宇

(1.江苏省电力公司电力科学研究院，江苏 南京 211103；2.江苏省电力调度控制中心，江苏 南京 210024)

近年来，在建设智能电网新形势的要求下，电网状态估计技术得到了长足的发展：不仅建立了更完整、更详细的电网模型，而且可为高级应用程序提供更灵活的扩展接口，从而为电力系统分析的在线化提供了有力的数据支撑[1]。在此基础上，江苏省电力调度控制中心于2012年12 月部署了在线安全稳定分析（DSA）系统。DSA 系统基于状态估计提供的实时电网运行方式与量测数据，对电网进行不间断的在线稳定分析，内容包括静态安全分析、暂态安全分析等六大类计算。同时，江苏电网已经全面部署了广域测量（WAMS）系统，全网各节点装设的向量测量单元（PMU）以每秒100 帧的采样率采集节点功率、电压、发电机相角等信息，通过高速网络传输至位于调度中心的控制主站，并存储于大型数据服务器[2]。DSA 与WAMS 系统的建立，为电网事故的在线监测、辅助决策、回溯分析提供了极大便利[3，4]，是建设智能电网的重要基础。

在应用DSA 进行事故反演计算的过程中，可能出现仿真曲线与实际PMU 录波曲线在形态上极为相似，但Prony 分析结果差异较大的状况。原因在于Prony 算法对于噪声较为敏感[5]，PMU 测量信号在测量、转换、传输过程中引入噪声干扰导致Prony 分析结果明显偏离实际。经验模态分解（EMD）是一种滤波算法，通过选择合适的本征模式函数（IMF）阶数，可构成自适应的高通、低通、带通或带阻滤波器[6]。然而，EMD 算法存在固有的不确定性及模态混叠问题，对于信噪比较低的信号，处理能力有限。

1 随机噪声特性分析

电力系统测量量在采集、转换、传输过程中，往往存在各类随机扰动。因此，研究随机噪声的数学特性，寻找随机噪声的抑制措施是十分必要的。

1.1 随机噪声的数学表示

随机噪声是由多种复杂因素造成的，包含着随机性与不可测性，在数学上可以近似用高斯白噪声模型表示，其定义如下：

（1）信号的幅值满足高斯分布，即其概率分布为正态函数；

（2）信号的平均期望为0；

（3）信号的二阶矩不相关，一阶矩为常数，即前后信号无关联。

理论上高斯白噪声为一无限长序列。但在工程应用中，在随机噪声信号序列足够长的情况下，也认为其近似满足以上性质。

1.2 随机重排—累加平均对随机噪声功率的影响

信号的强度可以用其功率来描述。对于长度为N的离散信号序列n0（i），其功率定义：

将序列n0（i）进行随机排序得到序列（i），由于（i）与n0（i）相比仅仅是各元素位置改变而幅值并未改变，故序列（i）的功率与原序列相同：

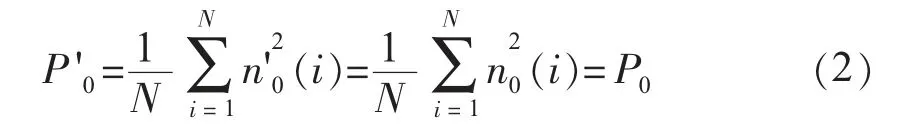
与原信号平均得到一次重构后的新信号n1（i）：

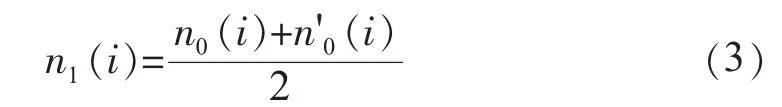
考察重构信号的功率变化情况，则：

即：

式（5）中等号成立的条件为：

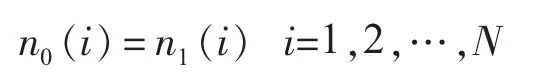
对于一般的随机噪声信号，上式成立的可能性是极小的。可见，通过随机排序—累加—取平均操作，可以降低噪声信号能功率。

如果重复以上随机重排—累加平均操作，得到新信号n2（i），n3（i），…nL（i），则重构信号的功率不断降低。当循环次数L 趋近于无穷大时，信号nL（i）趋近于一常数序列。对于白噪声信号而言，由于E[nL（i）]=0，故信号nL（i）的功率趋近于0。

构造随机噪声信号序列n0（i）如图1 所示。信号采样频率为100 Hz，共1001个采样点。

图1 随机噪声信号

对噪声信号进行随机重排—累加平均操作，迭代次数为10 次，计算每次迭代得到新信号的功率，信号功率P 随迭代次数n的变化趋势如图2 所示。

图2 噪声功率与迭代次数关系

信号功率随迭代次数增加而减小。迭代4 次之后，信号的功率已经降至原始信号的10%以下，随着迭代次数增大，随机噪声信号的功率趋近于0。

2 Prony 算法与EMD 算法性能比较分析

Prony 算法与EMD 算法是2 种常用的信号辨识算法。Prony 分析通过对信号进行拟合，得到信号中包含模式的频率、阻尼比等参数。EMD 具有时变、自适应等特性[7，8]，在各领域得到了广泛的应用。本节基于测试信号，对Prony 算法与EMD 算法对于含噪信号的辨识能力进行对比分析。

2.1 测试信号

为了考察2 种算法对于实际含噪信号的处理能力，构造以下测试信号：

其中：

测试信号的波形如图3 所示。信号的各分量参数如表1 所示。

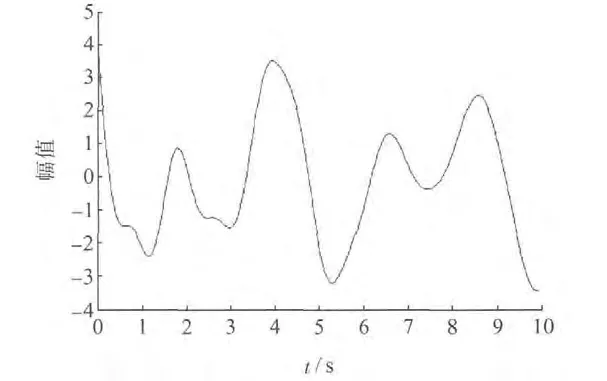
图3 测试信号的波形

表1 信号的各分量参数

在原始信号上叠加6.9 dB 白噪声干扰（信号信噪比为2），如图4 所示。

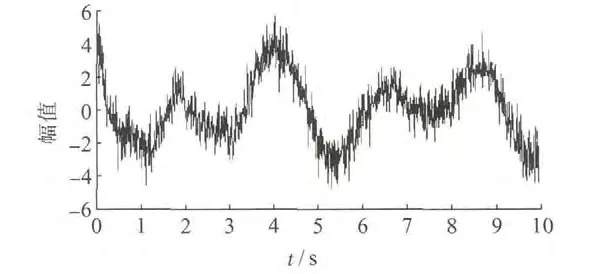
图4 含随机噪声的信号波形

2.2 Prony 算法对于含噪信号的处理能力

Prony 算法要求输入信号y为等间距采样的时间序列，假设该数据序列由一组具有任意振幅、频率、初相位和衰减因子的指数函数线性组合而成：

式（8）中：A为幅值；α为衰减因子；f为振荡频率；θ为初始相角。

测量输入x（0），…，x（N-1）的估计值可以表示为：

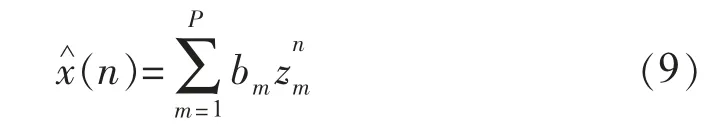
Prony 算法的计算步骤如下。

（1）构造二阶矩样本矩阵。定义二阶矩样本函数如下：

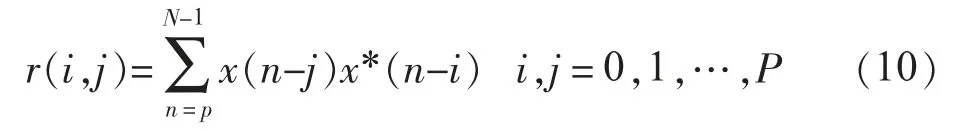
式（10）中：N为数据采样点数；P为样本矩阵阶数；采样数据为实数序列。

则二阶矩的样本矩阵形式：

为了使样本矩阵全面反映系统信息，维数L 取其最大值N/2。

（2）确定计算阶数。通过一定的规则确定模型阶数p，通常采用奇异值分解方法（SVD）进行。

（3）求解回归参数。求解以下方程组得回归（AR）参数，其中εp为最小误差能量：

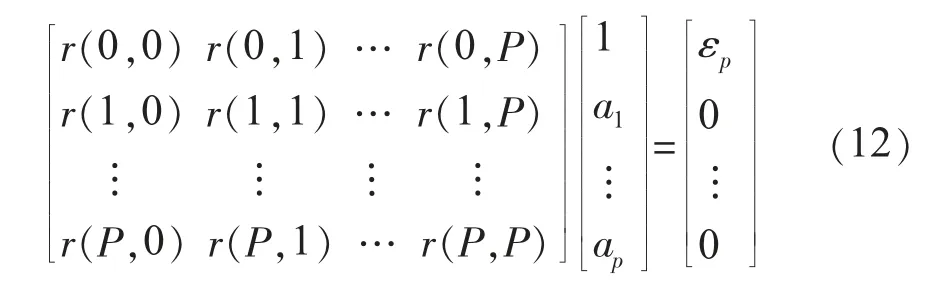
（4）求解特征方程。特征方程形式为：

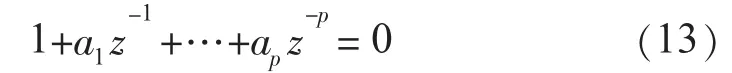
求解得到了特征根zi（i=1，2，…，P），称为Prony极点。

（5）求解b 向量。式（10）可以写成矩阵形式：

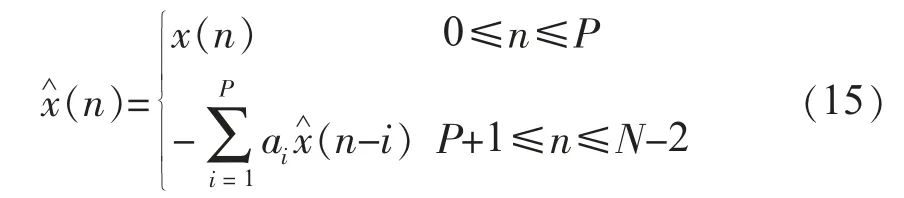
（6）求解各分量参数。通过求解线性方程组得到系数bm和Zm之后，可以根据如下公式得到各振荡分量的参数：

对无噪声扰动的原始信号进行Prony 分析，结果如表2 所示。

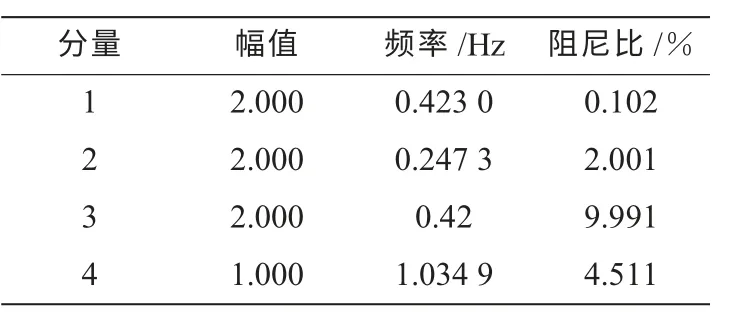
表2 原始信号的Prony 分析

在无噪声干扰时，Prony 算法可精确提取信号各分量的频率、幅值、阻尼比等参数，计算值与真值差异极小。对含噪声信号进行Prony 分析，结果如表3 所示。

表3 含噪信号Prony 分析

由表3 可见，随机噪声对Prony 分析影响较大，分析结果中出现幅值较大，而阻尼较弱的虚假模式，如模式1、模式2 等，真实分量淹没在噪声中。因此在对电力系统量测信号进行Prony 分析之前，需加入前置滤波环节，以削弱或消除噪声的影响。

2.3 EMD 算法对于含噪信号的处理能力

EMD 算法将复杂信号分解为一系列简单基本的固有模态函数分量，以便于提取各个分量的幅值、相位等信息，具体过程为：

（1）对于信号序列s（t），找到其极大值点和极小值点；

（2）对极大值点序列和极小值点序列利用三次样条插值进行拟合，得到极大值点包络线v1（t）和极小值点包络线v2（t），取；

（3）将m 从s（t）中减去，h=s（t）-m；

（4）将h 作为新的s（t），重复操作（1）至（3），直到极值点的包络线平均值m 趋于0，令c1=h，则c1为第一个IMF 信号；

（5）求余量r=s（t）-c1；

（6）将r 视为新的s（t）重复以上过程，求取第二个IMF 信号c2，第三个信号c3，直到余量r 因极值点过少而不能再进行分解。此时r为一个趋于平稳的量。

传统EMD 滤波算法的过程为：

（1）对原始信号进行EMD 分解，得到若干个IMF 分量与一个趋势分量；

（2）在噪声分量集中在信号的高频段，且真实信号功率远大于噪声功率的前提下，直接抛弃前n个IMF 分量；

（3）取其余IMF 分量与趋势分量重构，得到滤波后信号。

在实际操作中，如何确定抛弃IMF 分量的阶数n是值得研究的问题。通常采用的方式是计算各分量的功率，找到功率发生突变的分量，用该分量及其后的所有分量重构原信号。该方法的基础是认为信号中主导模式的功率远大于噪声分量的功率。在信号信噪比较高的情况下，这种直接抛弃前面若干个功率较低IMF分量，取余下IMF 作为主导模式分量的方法，可以较为精确地重构原始信号。但在信噪比较低的情况下，噪声信号功率接近甚至超过主导模式分量，功率判据失效，因而舍弃IMF 分量的个数通常难以确定。同时，由于EMD 算法存在固有的不确定性及模态混叠效应，不能保证抛弃的IMF 中不包含有用信息。因此，在信噪比较低的情况下，采用传统EMD 算法往往不能很好地达到去噪目的。例如，对第1 节中的含噪信号进行EMD 分解，得到7个IMF 分量与1个剩余趋势分量，如图5 所示。

从分解结果可以看到，分解得到的前3个分量均为高频噪声分量，但IMF 4，IMF 5的2个分量既包含噪声，也包含原始信号中的信息。如果直接丢弃，重构信号将会失去原始信号中的部分信息，导致重构信号与原始信号之间有较大差异。

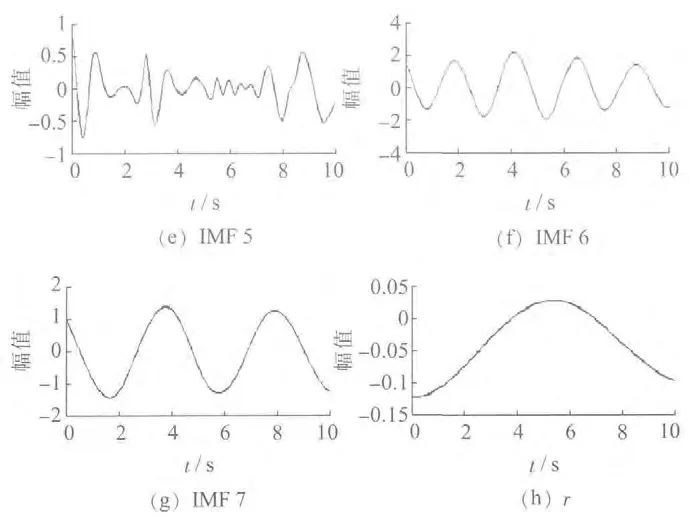
图5 含噪声信号的EMD 分解结果

3 基于EMD 滤波的Prony 算法

由上节分析可知，对于信噪比较低的信号，使用单一的EMD 算法或Prony 算法均难以达到理想效果，因此，利用EMD 算法的去噪特性，将其作为前置滤波环节，对降噪后的信号进行Prony 分析，是可以考虑的方法。基于对噪声统计特性的分析，可以考虑首先通过随机排序—叠加平均手段降低EMD 分解所得噪声分量的功率，再与其他分量进行重构，达到提高信噪比的目的。算法过程为：

（1）对原始信号y0（i）进行EMD 分解，并认为分解得到的第一个IMF 分量为随机噪声信号n0（i）；

（2）对n0（i）进行随机排序，得到信号（i），取2者平均值，；

（3）将n1（i）作为原始信号，重复步骤（2）的操作，得到功率降低的噪声信号nL（i）；

（4）将nL（i）于EMD 分解得到的除第一个IMF外的其余分量重构，得到信噪比改善的信号y1（i）；

（5）若需要进一步提高信噪比，则重复步骤（1）至（4），得到新信号y2（i），y3（i），…yM（i）。

应用上述方法，针对含噪信号EMD 分解结果中第一个IMF 分量，采用随机重排—累加平均抑制其功率（迭代次数为10），与其他7个分量重构，得到信噪比提高的信号序列，如图6 所示。与原始含噪信号（图4）相比，信号信噪比有所改善。为了进一步提高信号信噪比，继续对信号进行降噪循环，将历次循环得到结果与真实信号进行对比，如图7 所示。

由图7 可看到，经过3 次降噪得到的信号已经与真实信号较为接近。对降噪后的信号进行Prony 分析，结果如表4 所示。

图6 第一次降噪结果

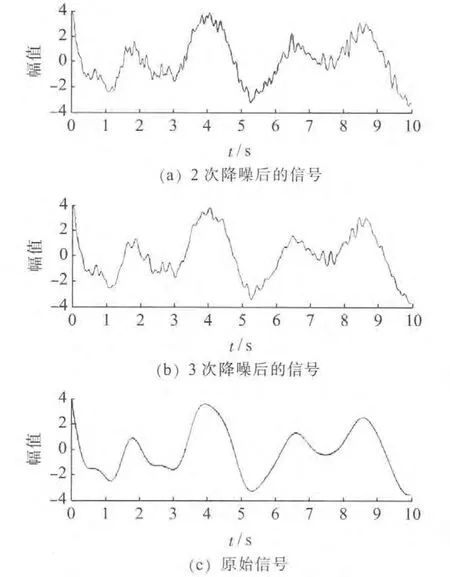
图7 降噪信号与原始信号对比

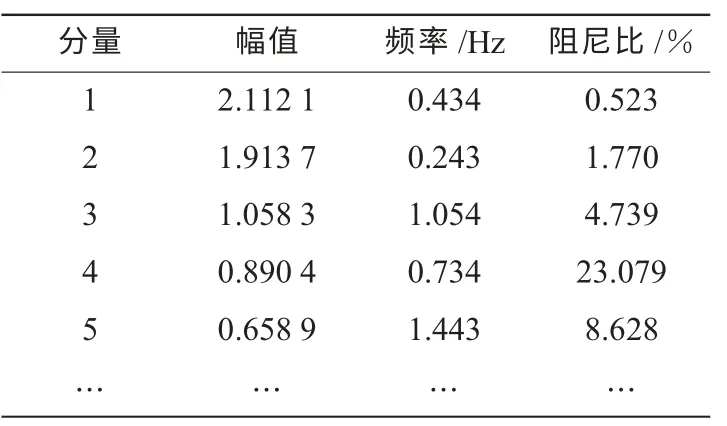
表4 降噪信号的Prony 分析结果

经过3 次降噪后的信号，Prony 分析结果与真实信号接近，其中分量1，2，3 均为原信号中的主导模式，幅值、频率等参数计算误差均在工程可接受范围内。可见基于噪声统计特性的EMD 算法可以有效抑制信号中随机噪声的功率，作为Prony 算法的前置滤波环节，可以削弱噪声对Prony 分析的影响，提高分析的精确程度。

4 江苏电网故障后分析

2014年4 月4 日15:33，江苏电网发生故障，渎车5249 线A 相单相短路，重合不成功跳三相。江苏省电力调度控制中心应用DSA 与WAMS，开展了事故后分析工作。调阅事故时刻PMU 录波曲线，线路三相跳开后，利港电厂1 号机有功振荡情况如图8 所示。

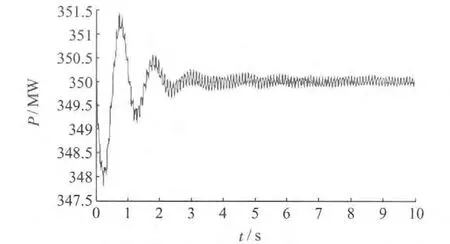
图8 利港1 号机有功PMU 录波曲线

利港厂1 号机在故障后功率第一摆峰峰值在3.2 MW 左右，5 s 后振荡趋于平息，显示系统阻尼特性良好。PMU 录波曲线中包含明显的随机噪声扰动。应用基于噪声统计特性的EMD 算法对PMU 录波信号进行2次滤波去噪，结果如图9 所示。

图9 滤波后的有功振荡曲线

从滤波结果可见，算法对于信号中的随机噪声扰动，有较好的抑制效果。对滤波后的信号进行Prony 分析，结果如表5 所示。

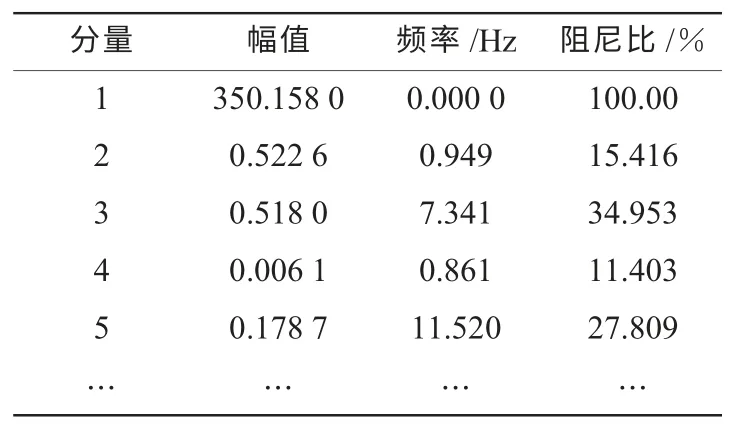
表5 PUM 曲线的Prony 分析结果

计算结果中，模式1为直流分量，模式2为振荡的主导模式，其频率为0.949 Hz，阻尼比为15.416%。其余模式幅值较小或阻尼比较强。基于当时刻数据断面，应用DSA 进行事故的反演仿真，事故后利港电厂1 号机有功振荡情况如图10 所示。

仿真结果曲线与PMU 录波曲线在形态上比较接近。对曲线进行Prony 分析，结果如表6 所示。

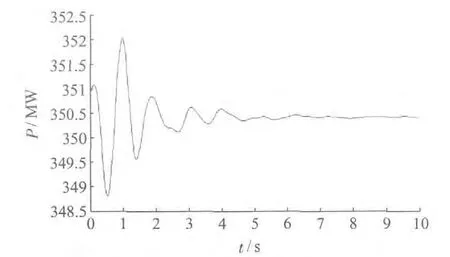
图10 利港1 号机有功振荡仿真曲线

表6 仿真曲线的Prony 分析结果

Prony 分析表明，仿真曲线主导模式频率为0.965 Hz，与PMU 录波曲线相符；仿真曲线阻尼比为13.249%，与PMU 录波曲线接近，但仍存在一定的差异，考虑到江苏DSA 中，全网所有机组均未建立一次调频模型，仿真曲线阻尼比较实际略低是可以理解的。同时，曲线比对结果证明，建立电网详细、完整的模型，尤其是发电机动态模型，对于提高DSA的仿真精度是十分重要的。

5 结束语

在电网故障反演计算过程中，时常出现PMU 量测信号中的随机噪声严重影响信号Prony 分析精度，导致分析结果出现大量虚假模式，淹没主导模式的情况。噪声的统计特性研究表明，随机排序—累加平均操作可以降低随机噪声的功率，随着迭代次数的增加，噪声功率趋近于零。本文在此基础上，提出将基于噪声统计特性的改进EMD 算法作为Prony 算法的前置滤波环节，对原始PMU 录波曲线进行降噪，提高了Prony 算法的精度。江苏电网2014年4 月4 日渎车5249 线故障后仿真分析算例表明，该算法可以显著提高PMU 测量信号的信噪比，滤波后信号中的噪声分量得到了明显抑制，其Prony 分析结果与DSA 仿真曲线可以取得较好的一致性。

[1]刘辉乐，刘天琪.电力系统动态状态估计的研究现状和展望[J].电力自动化设备.2005，24（12）：73-77.

[2]戴则梅，葛云鹏，张珂珩，等.电网广域监测系统的数据库集成方案[J].江苏电机工程，2013，32（1）：1-4.

[3]李碧君，许剑冰，徐泰山，等.大电网安全稳定综合协调防御的工程应用[J].电力系统自动化，2009，32（6）：25-30.

[4]戴则梅，陆进军，闪 鑫，等.PMU 数据在控制中心的集成应用[J].江苏电机工程，2012，31(2)：8-11.

[5]王铁强，贺仁睦，徐东杰，等.Prony 算法分析低频振荡的有效性研究[J].中国电力，2001，34(11)：38-41.

[6]郭 瑞.微网短期负荷预测中的白噪声分离[D].天津：天津大学硕士学位论文，2010.

[7]胡昊明，郑 伟，徐 伟，等.Prony 和HHT 算法在低频振荡在线辨识中的适用性比较[J].电力系统保护与控制，2013，41（14）：33-40.

[8]王 婷.EMD 算法研究及其在信号去噪中的应用[D].哈尔滨：哈尔滨工业大学博士学位论文，2010.