深海SPAR平台垂荡-纵摇耦合运动Mathieu稳定性分析

桑 松，石 晓，李长东，徐学军

（1.中国海洋大学，山东 青岛266100；2.河海大学，南京210098；3.四川大学，成都610065；4.海洋石油工程（青岛）股份有限公司，山东 青岛266555）

0 引言

随着深海海洋资源的开发，越来越多的浮式海洋平台投入运营。深海SPAR平台由于其自身重心低、水线面小、垂荡幅值小、初期投资低等特点，在全世界范围内得到了广泛应用。但由于其自身结构特点，其垂荡与纵摇固有周期比接近1∶2，当外界激励满足一定条件时会出现混沌和分叉等不稳定运动［1-3］。Jun B.Rhoh和Hang S.Choi［4］对规则波中经典Spar平台的马休不稳定性进行了研究，指出当平台的纵摇固有周期与垂荡固有周期比近似为2：1时，即使波高较小，也会发生纵摇的不稳定运动。通过数值和试验结果的比较，证实了Spar平台在纵摇固有周期为垂荡固有周期的2倍时最容易失稳。

1 平台运动方程的简化

由于平台在深海中受到的首摇激励力矩很小，并且由于Spar平台横向和纵向是对称的，所以平台的运动可以简化为一个三自由度的运动方程［5-7］：

由于只研究Spar平台的垂荡-纵摇耦合运动，所以只用（1）中的后两式。其中垂荡方向合力和纵摇方向的合力矩分别为：

式中：FR为辐射力；FW为波浪激励力；FWD为波浪漂移阻尼力；FM为系泊力；FHS为静水回复力；FCurrent为流力；FWind为风力；MR为辐射力矩；MWD为波浪漂移阻尼力矩；MW为波浪激励力矩；MM为系泊力矩；MHS为静水回复力矩；MWind为风力矩；MCurrent为流力矩。

不考虑风、流及二阶力的作用，应用简化方法研究平台主体垂荡-纵摇耦合运动，忽略波浪漂移阻尼力、波浪漂移阻尼力矩、风力、风力矩、流力和流力矩对Spar平台主体的影响，方程（1）可进一步简化为：

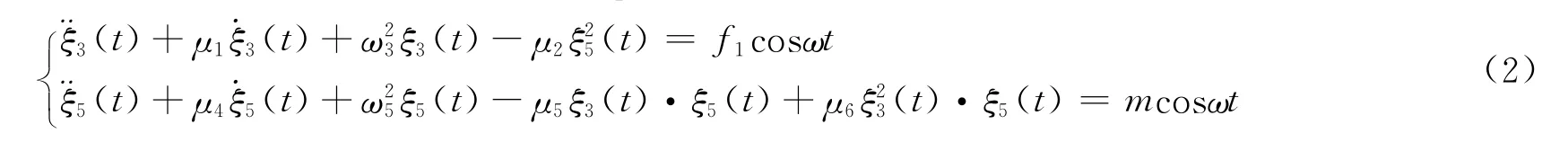
2 马休稳定性分析

大的垂荡运动能产生随时间变化的函数，从而对纵摇回复力矩产生影响。纵摇响应发生大幅振动的机理是垂荡运动的幅值达到一定程度之后，使纵摇运动方程变成一个大激励幅值的参数激励系统。

2.1 理论分析

马休方程的参数激励项随时间的变化规律是简谐的，是希尔方程的特例（参数激励是一般的周期函数）。希尔方程的标准形式为：

式中：p（t）为周期函数，由于仅讨论随时间简谐变化所激起的振动，故令p（t）＝βcost，希尔方程则转化为马休方程：

有阻尼马休方程的一般形式为：

在式（2）中，假设垂荡运动仅含一个谐波项并且忽略波面升高及二阶耦合对纵摇响应的影响，则垂荡运动可表示为ξ3（t）＝ξ3cosω3t，ξ3、ω3分别为垂荡运动幅值、固有频率。这样纵摇运动可表示为：

令τ＝ω3t，式（6）可以得到以下简化：

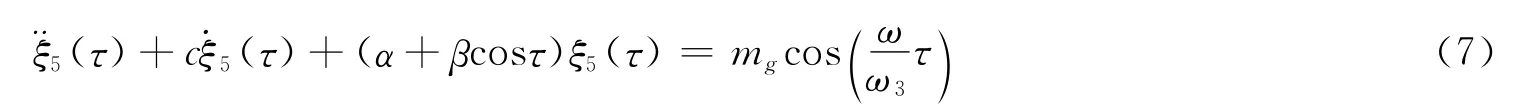
令式（7）的等式右边为零，则纵摇运动方程转化为标准的马休方程：

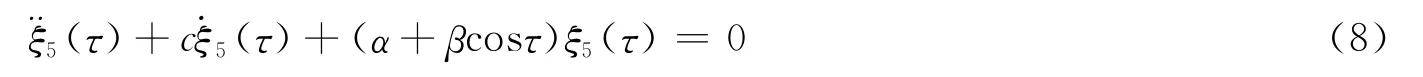
马休方程的稳定性由参数α，β决定。为了得到不同（α，β）的稳定性图谱，将方程以2π为周期的解定义为：

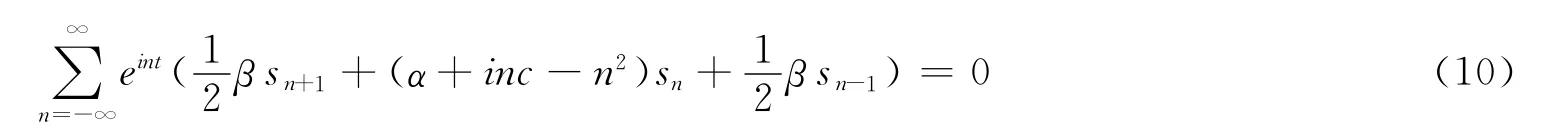
仅当所有的系数为零时，式（10）才能成立：

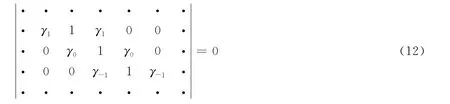
要使式（11）有非零解，则这个无限系数的行列式的值必须为零，其中α≠n2。其对应的行列式为：

同理，将方程以4π为周期的解定义为：

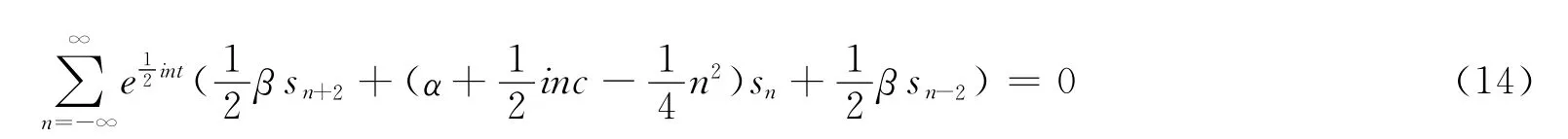
仅当所有的系数为零时，上式才能成立：

要使上式有非零解，则这个无限个系数的行列式值必须为零，其中α≠n2。其对应的行列式为：

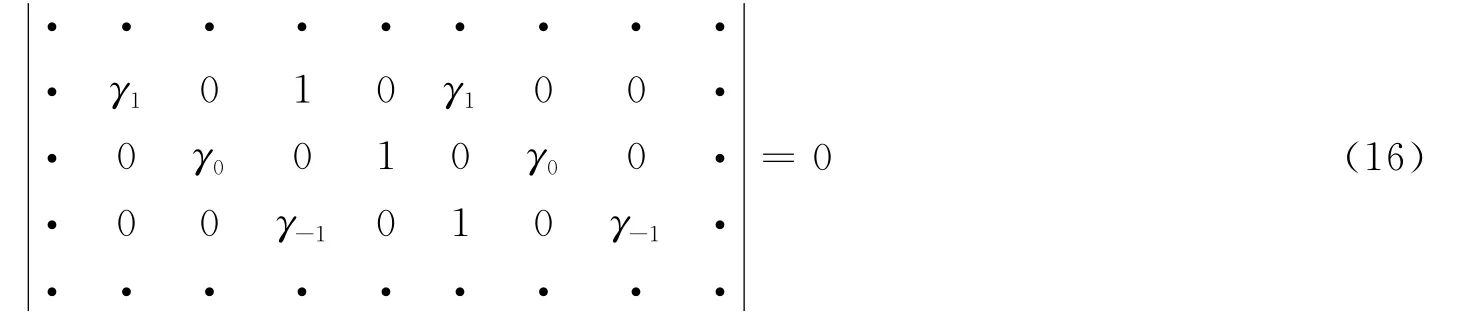
由解周期为2π，4π得到的两行列式（12）和（16），并且取不同的阻尼比，可得到马休稳定性图谱（如图1所示）。

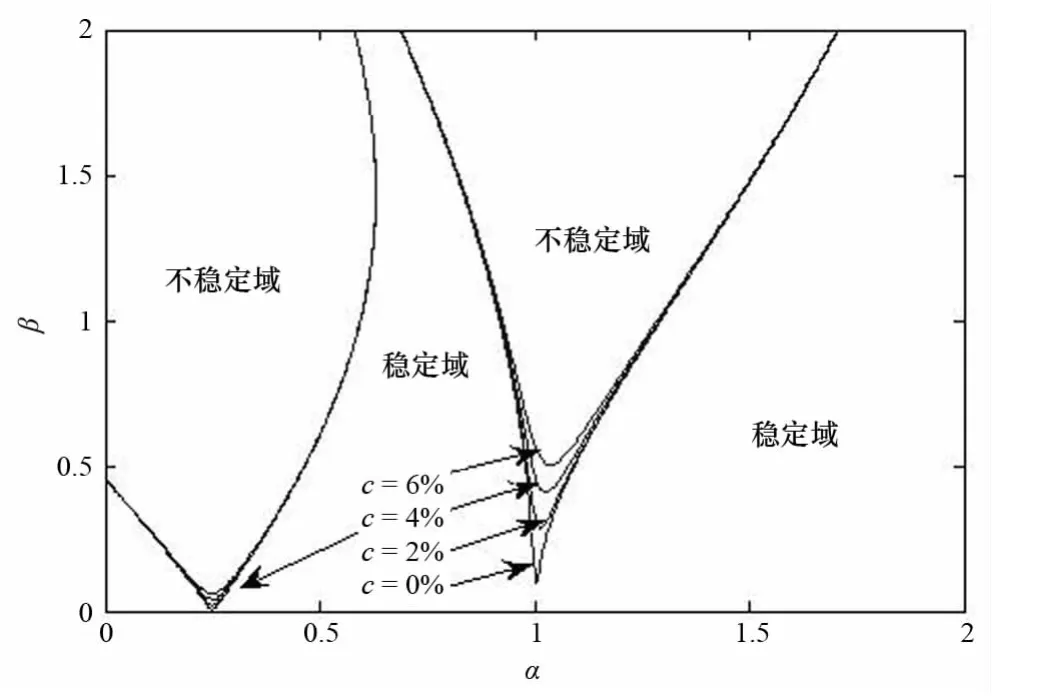
图1 马休稳定性图谱

可以看出，解周期为2π对应的稳定区域受到阻尼比变化的影响较大。当系统加上阻尼后，不稳定区域远离α轴，说明添加阻尼之后不稳定区域变小了。尽管如此，在解周期为2π对应的稳定区域受到阻尼比变化的影响还是有限的。一般情况下Spar平台垂荡纵摇频率之比在2∶1附近，对应α值在0.25附近，所以可以只考虑马休稳定解周期为4π的情况。当垂荡纵摇频率之比为2∶1，即α＝0.25时，不稳定区域最大，所以在进行平台设计时要尽量使平台纵摇固有频率远离垂荡固有频率的一半。

2.2 算例分析

以某一JIP SPAR平台［11］参数为例，已知该Spar平台的垂荡、纵摇固有频率分别为0.216rad／s和0.105rad／s，两者频率之比接近2：1，将相关参数代入式（8）得到：

由此可见，Spar平台的α值一般不会大于1，故研究经典Spar平台垂荡-纵摇耦合非线性运动的马休稳定性问题时，可以仅分析马休方程周期为4π的解时的稳定性问题而忽略掉图1中α＞0.7的部分。

根据马休失稳的条件：（1）波浪频率等于垂荡固有频率；（2）垂荡固有频率等于纵摇固有频率的两倍，下面取波浪激励频率为0.216rad／s，逐渐增大波幅，分别取h＝0.1m、0.180m、0.182m和0.190m，观察纵摇响应发生马休失稳的过程。这四种波幅在图1中对应的（α，β）坐标分别处于稳定域、临界线、不稳定域、不稳定域中。图2～图5分别对应四种不同激励状态下的垂荡、纵摇响应情况。

由图2可以看出，当波幅为0.1m时，因为垂荡运动发生共振，所以虽然波浪幅值较小，垂荡幅值仍然达到了7m，响应频率等于垂荡固有频率，响应处于稳定状态；纵摇响应幅值很小，响应频率等于波浪激励频率，能量稳定，处于稳定状态。

由图3可以看出，当波浪幅值为0.180m时，垂荡运动幅值在1 500s之前缓慢增大，最终稳定在11m左右；观察纵摇响应，此时纵摇幅值依然很小，但当垂荡幅值达到11m时，纵摇响应幅值开始增大，并且响应频率中开始出现纵摇固有频率成分，由纵摇相图可知，此时纵摇响应能量在不断发生变化，马休不稳定现象开始发生。

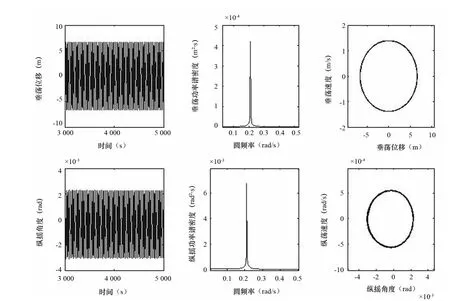
图2 垂荡纵摇时域响应（波幅0.1m，频率0.216rad／s）

图3 垂荡纵摇时域响应（波幅0.180m，频率0.216rad／s）

由图4可以看出，当波浪幅值为0.182m时，垂荡响应与波幅为0.180m时的情况相似，而纵摇在1 500 s之后响应幅值急剧增大，其响应频率中波浪激励频率成分急剧减少，同时由相图也可以发现，纵摇响应能量是在不断增大的。可见，此时垂荡响应能量已经达到饱和，波浪激励能量被传递到纵摇，导致了剧烈的纵摇响应。

图4 垂荡纵摇时域响应（波幅0.182m，频率0.216rad／s）

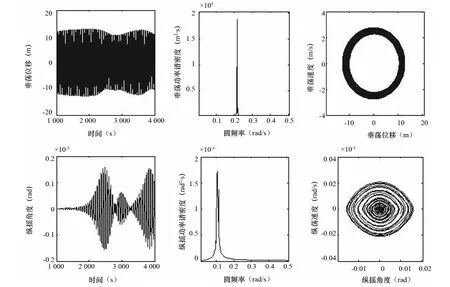
图5 垂荡纵摇时域响应（波幅0.190m，频率0.216rad／s）

由图5可以看出，当波浪幅值达到0.19m时，垂荡响应幅值仍然在11m左右，但是在3 000s附近有一定减小，此时对应纵摇响应幅值的极大值，出现了无周期运动现象。纵摇响应频率为其固有频率，并且出现了0.2rad的大幅纵摇响应，运动处于不稳定状态。

3 结论

通过以上数值分析可知：当波浪频率与垂荡固有频率相同时，由耦合导致的纵摇马休非线性运动不一定发生，这取决于波浪激励作用引起的垂荡运动的幅值的大小，只有当垂荡幅值达到一定程度，才会引起纵摇大幅不稳定运动的失稳现象，因此在平台参数确定的情况下，垂荡幅值的增大是导致纵摇响应由稳定过渡到不稳定的主要原因。此外，纵摇响应由稳定状态进入不稳定状态的过程中，纵摇响应频率成分会由以激励频率为主逐渐过渡到以纵摇固有频率为主。

［1］董艳秋.深海采油平台波浪载荷及响应［M］.天津：天津大学出版社，2005.

［2］曾晓辉，沈晓鹏，吴应湘.深海平台分析和设计中的关键力学问题［J］.船舶工程，2005，27（5）：18-21.

［3］RAN Zhihuang.Coupled dynamic analysis of floating structures in waves and currents［D］.Texas：Texas A＆M University，2000.

［4］Rho J B，Choi H S，Shin H S.A study on mathieu-type instability of conventional Spar platform in regular waves［J］.The International Journal of Offshore and Polar Engineering，2005，15（2）：104-108.

［5］张帆，杨建民.Spar平台的发展趋势及其关键技术［J］.中国海洋平台，2005，20（2）：6-11.

［6］Chakrabarti S K.Hydrodynamics of offshore structures：Mathematical theory and its applications in structures［C］.New York：Springer-Verlag New York Inc.，1987.

［7］Ma Q W，Patel M H.On the non-linear forces acting on a floating Spar platform in ocean waves［J］.Applied Ocean Research，2001，23（1）：29-40.

［8］Nayfeh A H.Perturbation methods［C］.New York：Wiley-VCH，1973.

［9］ZHANG Chenyi，Zhu C M，Lin Z Q.Theoretical and experimental study on the parasitically excited vibration of massloaded string［J］.Nonlinear Dynamics，2004，37：1-18.

［10］褚亦清，李翠英.非线性振动分析［M］.北京：北京理工大学出版社，1996.

［11］Halkyard J，Horton E H.Spar platforms for deep water oil and gas fields［J］.Marine Technology Society Journal，1996，30（3）：3-12.

［12］RAN Zhihuang.Coupled dynamic analysis of floating structures in waves and currents［D］.Texas：Texas A＆M University，2000.

［13］Ma Q W，Patel M H.On the non-linear forces acting on a floating Spar platform in ocean waves［J］.Applied Ocean Research，2001，23（1）：29-40.

［14］CHEN XiaoHong.Studies on dynamic interaction between deep-water floating structures and their mooring／tendon systems［D］.Texas：Texas A＆M University，2002.

［15］RAN Z，Kim M H.Nonlinear coupled response of a tethered Spar platform in waves［J］.International Journal of Offshore and Polar Engineering，1997，7：281-288.

［16］Koo B J，Kim M H，Randall R E.Mathieu instability of a spar platform with mooring and risers［J］.Ocean Engineering，2004，31：2175-2208.

［17］Rho J B，Choi H S，Shin H S.A study on mathieu-type instability of conventional Spar platform in regular waves［J］.The International Journal of Offshore and Polar Engineering，2005，15（2）：104-108.

［17］张海燕.Spar平台垂荡-纵摇耦合非线性运动特性研究［D］.天津：天津大学，2008.