几种插值方法在风压测试中的应用

王莺歌

(嘉应学院 土木工程学院，广东 梅州 514015)

0 引言

在利用风洞实验和现场实测进行风压分布研究的过程中，测点布置往往是风压变化剧烈的区域较密集，平缓的区域较为稀疏.在绘制分布图时，较为稀疏的点就需要用插值的方法获得其风压值.另外，实验中难以避免有“坏点”的出现，这些测点在分析时需要剔除，该位置的风压值也需要用插值等方法获取.本文引入地理统计学中数字高程模型概念，将实测得到的风压进行网格化处理，并利用多种插值方法获取待估数据，比较其优劣性.

1 DEM 网格化

数学高程模型(DEM)主要用于地理空间分析，是一种重要的地形数字化描述方法.［1～2］该模型以有序数列来代表各个点的高程，它呈现为规则格网点形式，主要包含两部分信息——平面位置信息和对应点的高程信息［3］.可利用等高线或者相似的模型获得，再使用插值的方法构造出完整数据［4］.在风压测试中，可以将风压分布图视作地形图，将风压值视作高程［5］.DEM 有很多形式，最为常见的是规则格网和不规则三角网，分别可简写为DEM 和TIN，见图1.

规则DEM 格网是利用一组二维等距离排列的点保存各点的高程信息，获取相关信息的方式有两种:直接来自规则网格，或利用离散点提供的信息插得到.TIN 则是一种采样系统，能够灵活选取采样点.所谓网格化过程其实就是无论测点是否规则布置，都将其坐标及高程数据通过一系列的数学计算，转换为规则网格形式的一种过程.其实质是首先利用高程点及等高线建立TIN 网格，然后以此为基础插值产生DEM 网格.

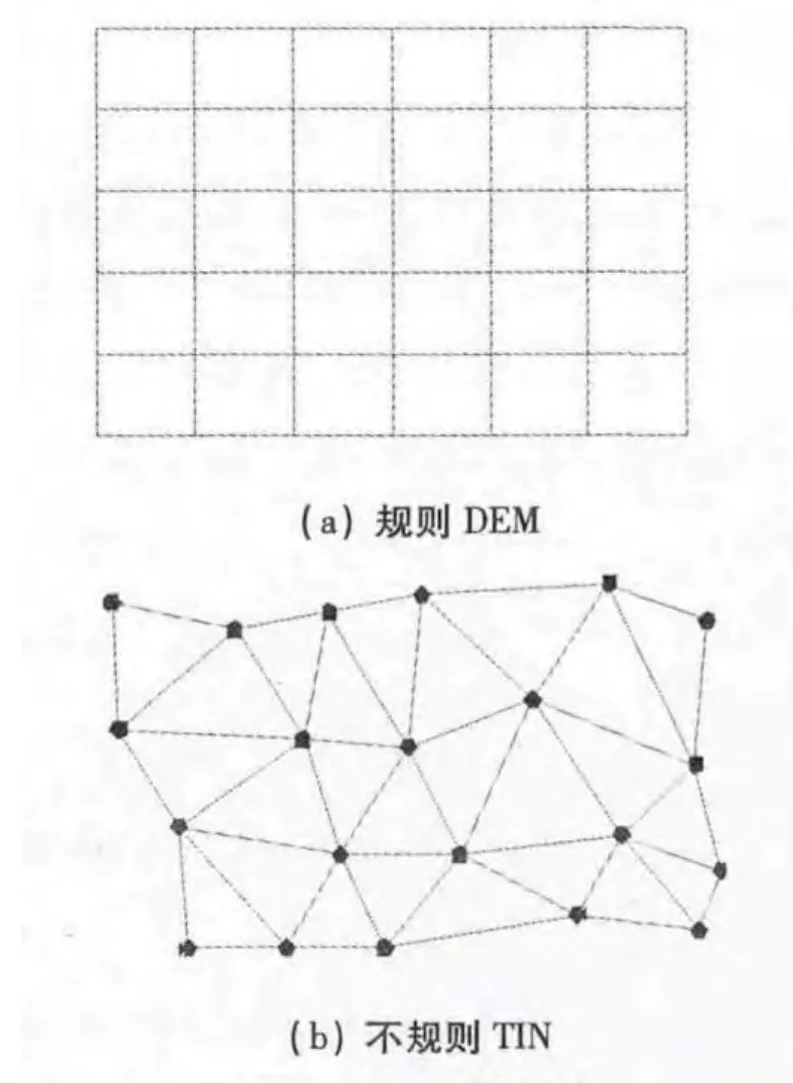
图1 DEM 网格形式

2 插值方法

常见的插值方法可依其数学本质和基本假设分为五大类［6］，表1 分别给出了这几类插值法的优缺点及其代表性方法［7，8］.

表1 常见插值法分类

2.1 最近邻点插值法

最近邻点插值法［9］是将测点的风压值赋给最近的网格结点，连接网格点，做中垂线，用其将整个计算域分隔成各子区域，每个子域的面积 作为权重系数，进行加权平均计算，计算结果可看作整个子域的属性，域内各点都具有该属性.最近邻点法的计算见式(1):

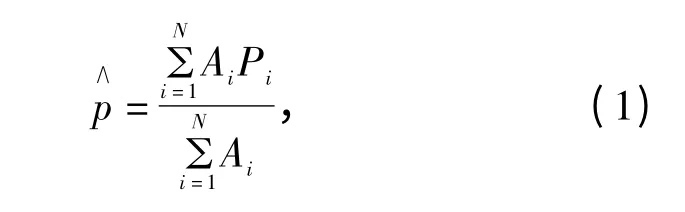
最近邻点插值在子区域内有固定值，适用于间隔非常均匀的情况.

2.2 距离反比法

距离反比法［10］属于精确插值法.待估算结点的风压等于各测点风压的加权平均值，其中权重系数是待估算结点与第 个测点距离的倒数.所以离结点近的测点所占的权重大.距离反比法预测风压的公式为:

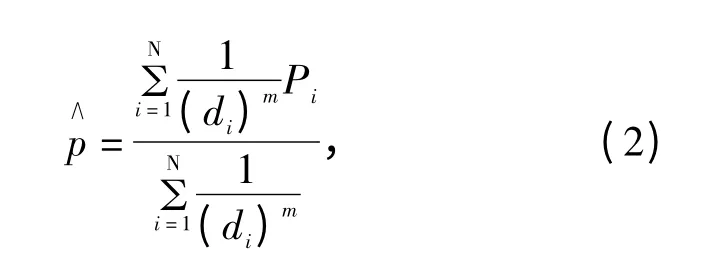
2.3 三角形线性插值法

三角形线性插［11］值属于精确插值，计算中将邻近的测点连成若干三角形，保证每条边都不与其它三角形的边相交，从而确定最佳的Delaunay 三角形.网格区域内由多个小的三角形组成整个平面，各结点都处于三角形中，结点的风压系数可通过求解三角形平面方程得到.当网格分布较均匀，且数据量适中时，三角形线性插值法的计算效果最好.

2.4 克里格插值

克里格插值法［12］是一种地理学统计内插方法，最初的建立是用于矿石勘测，现已广泛应用于各领域.在计算中需要考虑各方向尺寸、分布形式等采样区域的几何特征以及相关变量所包含的空间信息.为了满足无偏性和最小方差等条件，要设定一个权值，再用加权平均的方法预测待估区域风压.克里格插值法需要根据其空间分布确定变异图，据此计算出权值.在此基础上，通过平均法、移动窗口法等方式估算出各网格结点的风压值.由于空间统计方法是基于二阶平稳性假设之上的，所以它满足随机性、正态性、平稳性.图2 是克里格的计算流程.

图2 克里格插值法计算流程

3 工程实例

3.1 工程简介

以一坡度为30°的单坡屋面为例，图3 给出了其测点布置，图4 为其较低一侧迎风时的平均风压分布图.图3 中空心圆点和实心圆点都布置了测点，实心点为待研究的点.计算中将实心点数据去除，利用DEM 网格插值获得，并与实测点对比.

图3 测点布置图

图4 平均风压分布图

3.2 插值精度比较

针对以上单坡屋面分别使用:邻近点插值、距离反比插值、双线性插值、三角线性插值以及克里格插值法，估算图3 中实心圆点所标注的9 个测点的平均风压和脉动风压.因为所选的插值方法都属于精确插值，如果计算中控制待估测点与格网点重合，则可以得到这些点的实测风压.这一点是平滑插值法做不到的，平滑插值法主要是给出总的趋势，网格点的风压值并不能直接等于实测值.

图5 是屋面较低一侧迎风时，L1、L2、L3、M1、M2、M3、R1、R2、R3 等测点的平均风压和脉动风压估算误差结果.

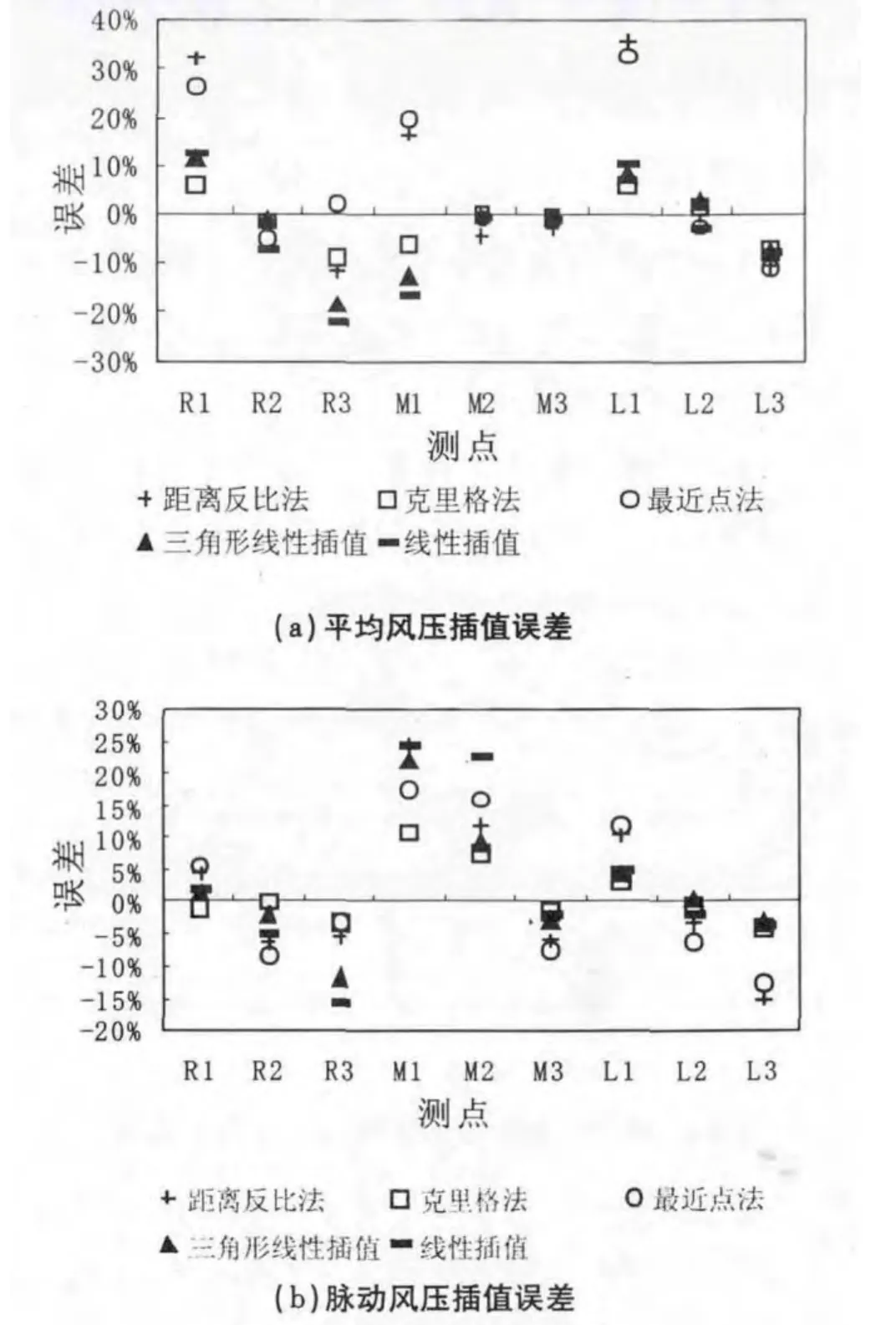
图5 结构表面风压插值误差比较

由图5 给出的误差分布可以看出，克里格法在各插值方法中的适应性最好，在屋面各点的插值误差都控制在一个可接受的范围内，尤其是在风压存在剧烈梯度变化的边角区域里，仍有较高的精度.三角形线性插值也具有较好的插值效果，由于各三角形子区域的顶点都是实测点，角部的测点较密，也保证了精度.双线性插值是更一般意义上的线性插值，其结果与三角形线性插值相类似，但稍逊与后者.距离反比法是工程实践中最常见的方法之一，但由于其仅将距离作为评价两点相关度的依据，没有综合考虑整个区域对待估点的影响，所以精度并不高.特别是在迎风的屋檐和远离来流的屋脊处误差相当的大，只有在中部风压变化平缓的地方才能够满足要求.最近点法也与之分布类似，在风压变化比较缓和的M2 点，最近点法的精度甚至高于其他一些方法.

4 结论

(1)使用DEM 网格化处理，可以由布置不规则的测点网格，通过内插生成规则网格，从而获得更详细的风压分布数据.

(2)克里格插值法具有较高的精度，适用于风压分布的插值计算，尤其是在风压梯度变化剧烈的地方还能够保持较好的计算效果.

［1］FRANKE R.Scattered Data Interpolation:Test of Some Methods［J］.Mathematics of Computations，1982，33(157):181-200.

［2］LAM N S.Spatial Interpolation Methods:A Review［J］.The American Cartographer，1983，10(2):129-149.

［3］李志林，朱庆.数字高程模型［M］.武汉:武汉大学出版社，2007.

［4］宋向阳，吴发启.几种插值方法在微DEM 构建中的应用［J］.水土保持研究，2010，17(5):45-50.

［5］王莺歌，李正农，吴红华，等.低矮房屋屋面脉动风压的预测［J］.振动与冲击，2013，32(5):157-162.

［6］李新，程国栋，卢玲.空间内插方法比较［J］.地球科学进展，2000，15(3):260-265.

［7］卢华兴.DEM 误差模型研究［D］.南京:南京师范大学，2008.

［8］张锦明，游雄，万刚.DEM 插值参数优选的试验研究［J］.测绘学报，2014.43(2):178-192.

［9］THIESSEN A H.Precipitation Averages for Large Areas［J］.Monthly Weather Review，1911，39(7):1082-1084.

［10］FRANKE R.Scattered Data Interpolation:Test of Some Methods［J］.Mathematics of Computations，1982，33(157):181-200.

［11］LEE D T，SCJACHTER B J.Two Algorithms for Constructing a Delaunay Triangulation［J］.International Journal of Computer and Information Sciences，1980，9(3):219-242.

［12］CRESSIE N A.C.The Origins of Kriging［J］.Mathematical Geology，1990，22(3):239-252.